特别相对论论论
Section outline
-
What happens when an object moves very fast?
::当物体移动速度非常快时会怎样?The theory of relativity refers to two different elements of the same theory: special relativity and general relativity. The theory of special relativity was first introduced by Albert Einstein in 1905 and was later (1916) considered to be a special case of the more comprehensive theory of general relativity .
::相对论理论指同一理论的两个不同要素:特别相对论和一般相对论。 特别相对论理论是艾伯特·爱因斯坦于1905年首次引入的,后来(1916年)又被视为比较全面的一般相对论的一个特殊案例。The special theory of relativity was accepted reasonably quickly by physicists considering that it was introduced in 1905 and widely accepted by 1920. The theory of general relativity was not accepted as quickly. Some physics historians insist that considerable to the theory existed even into the 1950’s and 1960’s. At least part of the problem for the acceptance of the theory was that some conclusions from the theory went against common sense and also, there was very little experimental evidence to support the theory.
::物理学家们相当迅速地接受了相对论的特殊理论。 考虑到该理论是1905年引入的,并在1920年被广泛接受,物理学家们相当迅速地接受了这一理论。 普遍相对论并没有很快被接受。 一些物理学历史学家坚持认为,即使在20世纪50年代和60年代,理论也存在相当大的存在。 接受理论的至少部分问题在于,理论的某些结论与常识背道而驰,而且支持理论的实验证据也很少。The special theory of relativity essentially explains how to interpret motion between different inertial frames of reference, that is, places that are moving at constant speeds relative to each other. Special relativity is based on two postulates:
::特别相对论理论基本上解释了如何解释不同惯性参照框架之间的运动,即以恒定速度相互相对移动的地点。 特殊相对论基于两个假设:-
The laws of physics are the same for all observers within their own inertial
reference frame
.
::所有观察者在其惯性参照框架内的物理定律都是一样的。 -
The
of light in a vacuum is the same for all observers regardless of their relative motion or the motion of the source of the light.
::真空中的光对所有观察员都是一样的,无论其相对运动或光源运动如何。
An inertial reference frame is one in which Newton’s first law , the law of , is valid. That is, if an object experiences no net force due to other bodies, the object either remains at rest or remains in motion with constant in a straight line.
::惯性参考框架是牛顿第一部法律 — — 法律 — — 的有效框架。 也就是说,如果物体没有受到其他机构的净力,则该物体要么处于休息状态,要么保持直线不变。A Closer Look at Postulate 1
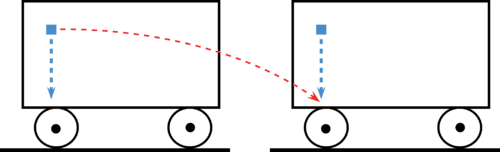
::更仔细地看一看1号假设Consider dropping a child’s toy block in a railroad boxcar.
::考虑在火车箱车里丢弃小孩的玩具。The block will fall straight down and come to rest on a spot directly underneath the position from which it was dropped. For an observer inside a stationary boxcar, there will be a measureable the block fell, a time required to fall and an for the fall. If the boxcar is moving at a constant horizontal velocity 10 m/s, the observer inside the boxcar will find the all measurements to be exactly the same as when the boxcar was stationary, including the spot where the block came to rest. For an observer inside the boxcar, the frame of reference is the same whether the car is moving or not and all the laws of physics will be the same in both cases.
::区块将直接倒下, 并倒在倒下的位置下方。 对于固定式箱式车内的观察者来说, 区块将有一个可以测量的跌倒时间、 需要的跌倒时间和跌倒时间。 如果箱式车以恒定水平速度10米/秒的速度移动, 箱式车内的观察者会发现所有测量结果都与箱式车是固定状态时完全相同, 包括区块的休息点。 对于箱式车内的观察者来说, 参照框架是相同的, 无论汽车是否在移动, 而在这两种情况下, 所有物理定律都是一样的 。Consider the block falling in the moving boxcar as observed by a stationary observer outside the boxcar. As observed in this frame of reference, the block does NOT fall straight down but rather follows a parabolic path. The distance it falls is NOT the same and the average velocity calculated is NOT the same. For the outside observer, the block has a constant horizontal velocity equal to the velocity of the boxcar and the vector sum of the horizontal velocity and the vertical fall result in the parabolic path sketched. For the inside observer, there is no horizontal velocity. For the outside observer, the distance traveled along the parabolic path is longer than the path straight down but the time for the fall is the same. For the outside observer, the average velocity is greater.
::以固定观察者在箱车外观察到的移动式箱车内坠落的区块为例。 正如在此参考框架中所观察到的, 区块不直接倒下, 而是沿着抛物线路径。 它的距离并不相同, 平均速度计算不相同 。 对于外部观察者来说, 区块的常态水平速度相当于箱车的速度, 水平速度和垂直下落的矢量和矢量总和导致所绘制的抛物线路径 。 对于内部观察者来说, 没有水平速度 。 对于外部观察者来说, 抛物线路径的距离比直下路径长, 但坠落的时间相同 。 对于外部观察者来说, 平均速度更大 。Inside each frame of reference, all the laws of physics hold, but the measurements are not the same between the two frames of reference.
::每一参照基准内,所有物理定律,但两个参照基准之间的测量结果不同。A Closer Look at Postulate 2
::更仔细地看一看2号假设Suppose you are sitting on the hood of a stationary car and your brother is standing alongside the road some 50 feet ahead of the car. If you throw a ball to your brother with a velocity of 10 m/s, it will travel, relative to you, at a velocity of 10 m/s and it will travel, relative to your brother, as 10 m/s. Suppose then, that you repeat the throw except this time, you toss the ball while the car is moving toward your brother at 10 m/s. This time, the ball will move, relative to you, with a velocity of 10 m/s but it will move, relative to your brother, with a velocity of 20 m/s. In this case, the velocity of the source of the ball is added to the velocity of the ball to get the velocity relative to a stationary observer.
::假设你坐在固定汽车的引擎盖上,而你哥哥站在汽车前面大约50英尺的路边。如果你将球投到你兄弟身上,速度为10米/秒,相对于你,它将以10米/秒的速度行走,相对于你,速度为10米/秒/秒。假设你重复投球,但这次除外,当汽车在10米/秒向兄弟移动时,你抛球。这次,相对于你,球将移动,速度为10米/秒/秒,但相对于你兄弟,它将移动,速度为20米/秒/秒/秒。在这种情况下,球源的速度将加入球的速度,以获得相对于固定观察员的速度的速度。Common sense would tell us that if we did this same experiment with light, that is, shine a flashlight off the hood of a moving car in the same direction the car is moving, the velocity of the light relative to a stationary observer would be increased by the velocity of the car. In fact, such an increase in the speed of light has never been found. In fact, in experiments carried out to test for the effect of the movement of the source on the speed of light (Michelson-Morley), the results indicate that the speed of light is completely unaffected by the motion of the source. It appears that the speed of light in a vacuum is constant regardless of relative motion. Hence, the suggestion in postulate 2. The speed of light in a vacuum is the same for all observers regardless of their relative motion or the motion of the source of the light.
::常识告诉我们,如果我们对光做同样的实验,即将闪光灯从移动汽车的引擎盖上照向汽车正在移动的同一方向,与固定观察者相比,光的光速会因汽车的速度而提高,事实上,光速的这种提高从未被发现,事实上,在试验源的移动对光速的影响时,结果显示光速完全不受来源运动的影响,真空中的光速似乎保持不变,而不论相对运动如何,因此,在假设2中,真空中的光速对所有观察者来说是一样的,不管其相对运动或光源运动如何,真空中的光速对所有观察者来说都是相同的。The special theory of relativity copes with the results of the Michelson-Morley experiments much better than does classical mechanics, but it also has some surprising consequences. For example, according to the theory of special relativity,
::相对论的特殊理论与Michelson-Morley实验的结果相比,比古典力学要好得多,但也有一些令人惊讶的后果。例如,根据特别相对论的理论,-
Two events that occurred simultaneously for one observer were not simultaneous for another observer if the two observers had relative motion to each other. (Relativity of simultaneity).
::一个观察员同时发生的两起事件,如果两个观察员相对地相互移动,对另一个观察员来说不是同时发生的。 (同时的相对性)。 -
Clocks in a moving frame of reference tick more slowly than an observer’s “stationary” clock. (Time dilation).
::移动参考框架的时钟比观察者的 " 静止 " 时钟慢。 (时间放大) -
Objects are measured to be shorter in the direction that they are moving with respect to a stationary observer. (Length contraction).
::物体相对于固定观察员而言,其移动方向被测量为较短。 (活度收缩)。 -
@$\begin{align*}E = mc^2\end{align*}@$
,
and mass are equivalent and transmutable. (Mass-energy equivalence).
::@$\ begin{ align}E = mc_ 2\ end{ end{ align} $, 质量是等效和可变的 。 (Mass- energy equality) -
No physical object can travel faster than the speed of light in a vacuum. (Maximum speed is finite).
::在真空中,任何物理物体的飞行速度都不能比光速快。 (最大速度是有限的)。
Launch the PLIX Interactive below observe two particles moving relative to each other:
::启动 PLIX 交互式的下面 观测两个相相对移动的粒子 :Time Dilation
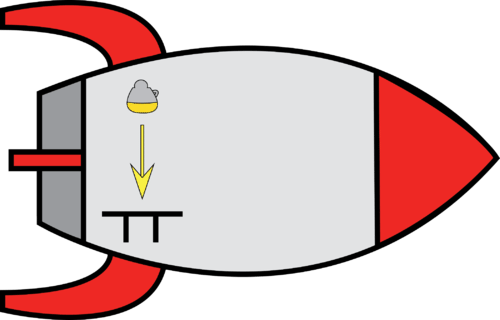
::时间关系Suppose we are in a rocket ship sitting at rest on the earth and we turn on an overhead light. The light will travel downward (and all other directions as well) and land on the table below. The observer in the rocket ship can measure the distance traveled to the table, the time required for the light to arrive on the table and an average velocity for the light. If the experiment is repeated in the rocket ship while the rocket is flying past the earth at a constant horizontal velocity, the observer inside will find all the measurements and calculations to be exactly the same as when the rocket was at rest.
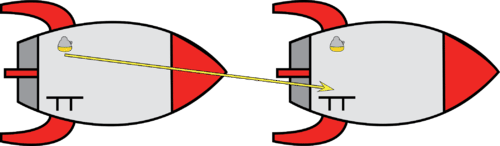
::假设我们坐落在一艘坐落在地球上的火箭船上,我们打开了上方的光线。光线会向下(以及所有其他方向)行驶,然后降落在下面的桌子上。火箭船上的观察者可以测量到到桌子的距离、灯光到达桌子所需的时间以及光的平均速度。如果在火箭船上重复试验,而火箭正以恒定的水平速度飞过地球,里面的观察者会发现所有测量和计算都与火箭在休息时完全相同。Suppose now that the rocket ship is flying past the earth at the same constant horizontal velocity and that the observer is stationary on the earth. For the observer in the rocket ship, the light falls down on the table traveling at the regular speed of light, @$\begin{align*}c\end{align*}@$ . For the observer on the earth, the light travels horizontally with the ship and also falls down onto the table. For the observer on the earth, the path appears to be longer since the light not only went downward but also horizontally.
::假设现在火箭飞船正以相同的水平水平速度飞越地球,而且观察者是静止的。对于火箭飞船的观察者来说,光线以正常的光速落在桌子上, @$\ begin{ align\\ c\ end{ ALign\ $. 对于地球上的观察者来说,光线与飞船水平水平地穿行,也跌到桌子上。对于地球上的观察者来说,路径似乎更长,因为光线不仅向下,而且向上。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-MDU4OGYwMzk0MGQ1NjM5ZGNkZDI4MDYwOTlhMzUxOWY.-vtq"> However, since we have postulate 2, it is not allowed for the light to travel farther in the same time and therefore have a greater average velocity. According to postulate 2, the speed of the light as observed inside the space ship by that observer must be <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="3%20%5Ctimes%2010%5E8%20%5C%20%5Ctext%7Bm%2Fs%7D"> @$\begin{align*}3 \times 10^8 \ \text{m/s}\end{align*}@$ and the speed of light observed by the observer on the earth (the light moving diagonally) must ALSO be @$\begin{align*}3 \times 10^8 \ \text{m/s}\end{align*}@$ .
::然而,既然我们有2号假设,光线不能在同一时间更远地飞行,因此平均速度更高。 根据2号假设,该观察者在太空船上观察到的光速必须@$\ begin{ align}3\ times 10_8\\ text{m/ end{ align}$ 和观察者在地球上观察到的光速( 光在对角移动) 也必须是@$\ begin{ allign}3\ times 10_ 8\\\ text{ m/ send{ allign}$ 。So, how is it possible for both observers to measure the speed of light as the same number when the distance traveled is clearly NOT the same? There is an unstated assumption involved here that indicates the passage of time in the two reference frames is the same and that is where the special theory of relativity changes our ideas. The special theory of relativity tells us that the observer on earth will see the clocks on the rocket ship ticking more slowly than his own clocks. So, while the observer on the rocket ship sees the light travel a distance @$\begin{align*}x\end{align*}@$ meters in 1.00 second as measured on his clock, the observer on the earth sees the light travel @$\begin{align*}2x\end{align*}@$ meters in 2.00 seconds as measured by his clock. In both cases, the speed of light is measured to be @$\begin{align*}c\end{align*}@$ . It is important to note that this is not an optical illusion or some strange effect on the mechanical operation of the clock, the actual time on the ship slows down compared to the time of the stationary observer. This is referred to as .
::因此,当距离明显不同时,两位观察家怎么可能将光速与相同数字测量为光速?这里涉及一个未说明的假设,表明两个参照框架的时间流相同,这就是相对论的特殊理论改变我们的想法。相对论的特别理论告诉我们,地球上的观察家将看到火箭船上的时钟比他自己的时钟慢得多。因此,当火箭船上的观察家看到光线在1.00米以内行驶@$\ begin{align{x\end{align}{align}$messum与他的时钟测量的距离为1分之差时差时,地球观察家会看到光线旅行@$\ begin{align}%2xend{align}}{align_$mum 以他的时钟测量的2. 00秒内。在两种情况下,光速测量为@ begin{al}cend{align}cend{align}{align}$。因此必须指出,这不是一个光幻象或机械操作时钟的奇怪效果。 实际时间指这个观察家在观察家的时段。The equation for time dilation is @$\begin{align*}\Delta T=\frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}\end{align*}@$
::时间扩张的方程式是 @ $\ begin{ align} Delta Tfrac\ Delta t\sqrt{ 1 -\ frac{ v\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\end{ ALign$\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZmYxZDM5MjI3NjE5MzYyMjkwNmFiZWI3YThmYjQyYjk.-tf7"> where <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="%5CDelta%20t"> @$\begin{align*}\Delta t\end{align*}@$ is the time interval between two events in the moving reference frame and @$\begin{align*}\Delta T\end{align*}@$ is the time interval as measured in a stationary frame of reference. “ @$\begin{align*}v\end{align*}@$ ” is the relative velocity of the moving reference frame and @$\begin{align*}c\end{align*}@$ is the speed of light in a vacuum.
::@$\ begin{ align} delta t\end{ align} $ 是移动引用框中两个事件之间的时间间隔, @ $\ begin{ align} Delta\ end{ end{ align} $ 是固定引用框中测量的时间间隔 。 “ @ $\ begin{ align} end{ align} $ 是在移动引用框中的相对速度 。 @ $\ begin{ align} c\ end{ align} $ 是真空中的光速 。It should be clear from the equation that if the relative velocity between the two frames of reference is zero, then @$\begin{align*}\Delta T=\Delta t\end{align*}@$ and there is no time dilation. We can also use the equation to show that for relative speeds like 100 m/s, which seems very fast to us, the comparison to the speed of light would show no noticeable time dilation.
::从方程式中可以清楚地看出,如果两个参照框架之间的相对速度为零,那么@$\ begin{ alignDelta TDelta t\end{align$, 并且没有时间推算。 我们还可以用方程式来显示,对于相对速度, 如100米/秒, 对我们来说似乎非常快, 与光速的比较不会显示明显的时间推算。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-p4x"> <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="%5CDelta%20T%3D%5Cfrac%7B%5CDelta%20t%7D%7B%5Csqrt%7B1-%5Cfrac%7Bv%5E2%7D%7Bc%5E2%7D%7D%7D%3D%5Cfrac%7B10%20%5C%20%5Ctext%7Bs%7D%7D%7B%5Csqrt%7B1-%5Cfrac%7B100%5E2%7D%7B(3%20%5Ctimes%2010%5E8)%5E2%7D%7D%7D%3D%5Cfrac%7B10%20%5C%20%5Ctext%7Bs%7D%7D%7B1-1%20%5Ctimes%2010%5E%7B-13%7D%7D%3D10%20%5C%20%5Ctext%7Bs%7D"> @$\begin{align*}\Delta T=\frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{10 \ \text{s}}{\sqrt{1-\frac{100^2}{(3 \times 10^8)^2}}}=\frac{10 \ \text{s}}{1-1 \times 10^{-13}}=10 \ \text{s}\end{align*}@$
::@ $\ begin{ align}\\ Delta Tfrac\ Delta t\\ sqrt{ 1\\\ frac{ v\\\ 2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-M2I2NDNlMDJjNjEyMjU5NGI4ZDFkZmY3NmNmM2ZjYzc.-tcw"> 100 m/s is so slow compared to the speed of light, that it makes no difference in the time dilation formula. In order for any noticeable effect to occur, the relative velocity of the reference frames must be a significant fraction of the speed of light. <br/> <span style="color: green; "> ::与光速相比,100米/秒的速度太慢,在时间膨胀公式上没有差别。要产生任何明显效果,参考框架的相对速度必须是光速的相当部分。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h4 id="x-ck12-MWJhNDdjMmI0ZjA3ZmMxMDNhNzQ5NWQ4NWQwOWRlZGQ.-h8e"> <strong> Example <span> 1 </span> </strong> <br/> <span style="color: green; "> ::例1 </span> </h4> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZTgwMzkzZTQ4YTU2NDE2NGZhZWIxZjI5NTBkNDczMDg.-zfz"> A muon has a rest lifetime of <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="2.2%20%5Ctimes%2010%5E%7B-6%7D%20%5C%20%5Ctext%7Bs%7D"> @$\begin{align*}2.2 \times 10^{-6} \ \text{s}\end{align*}@$ . If it travels with a speed of 0.95c relative to you, how far will you see it travel before it decays?
::moon 的休息寿命为 @$\ begin{ align}\ 2.2\ times 10\\\ 6}\\\ text{s\\\\\\ end{ align}$。如果其飞行速度与您相比为0.95c,那么在衰变之前你能看到它走多远?Muon’s lifetime according to your reference frame
::依据您的参照基准框架, Muon 的一生@$\begin{align*}\Delta T=\frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{2.2 \times 10^{-6} \ \text{s}}{\sqrt{1-\frac{(0.95 c)^2}{c^2}}}=\frac{2.2 \times 10^{-6} \ \text{s}}{\sqrt{1-0.90}}=7.0 \times 10^{-6} \ \text{s}\end{align*}@$
::@ $\ begin{ align} Delta Tfrac\ Delta\ Delt{ 1-\\ frac{ 1\\\ frac{ v\\\ 2\\\ 2\\\ frac} 10\\ 6}\\ text{s\\\ sqrt} 2\ 2\\\\\\ frac\\\\\ 10\ 6}\\ text{ s\\\ qrt{ 1-0.90\\\\ 7\ times 10\\ 6}\ text{ { end{ ALign}\\\\\\\ text{\\\\\\\\\\\\\\\\\\\\\ c\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-62g"> <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="%5Ctext%7Bdistance%7D%3D(3.0%20%5Ctimes%2010%5E8%20%5C%20%5Ctext%7Bm%2Fs%7D)(0.95)(7.0%20%5Ctimes%2010%5E%7B-6%7D%20%5C%20%5Ctext%7Bs%7D)%20%3D%202.0%20%5Ctimes%2010%5E3%20%5C%20%5Ctext%7Bmeters%20%7D"> @$\begin{align*}\text{distance}=(3.0 \times 10^8 \ \text{m/s})(0.95)(7.0 \times 10^{-6} \ \text{s}) = 2.0 \times 10^3 \ \text{meters }\end{align*}@$
::@ $\ begin{ align} text{ 距离{ (3. 0\ times 10_ 8\\ text{ m/ s} (0. 95) (7. 0\ times 10\-6}\\ text{s}) = 2. 0\ times 10\ 3\\ text{ 度量{ { end{ align} { </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-YTg2NzhmMWQ5MjNlZjZmMGQ5NGVjMGU1MTQ0NDJhMmU.-upa"> <span style="font-weight: 400;"> Launch the PLIX Interactive below to compare how two clocks behave - one stationary on the ground and another moving rapidly in a rocket: </span> <br/> <span style="color: green; "> ::用下面的PLIX互动来比较两时钟的行为----一个在地面固定,另一个在火箭中快速移动: </span> </p> <div class="x-ck12-video-object plix-fs" id="x-ck12-eyg"> <div class="iframe-wrapper ck12-no-annotation"> <iframe allowfullscreen="allowfullscreen" data-artifactlang="en" data-embed="PGlmcmFtZSBzcmM9Imh0dHBzOi8vd3d3LmNrMTIub3JnL2Fzc2Vzc21lbnQvdG9vbHMvZ2VvbWV0cnktdG9vbC9mdWxsc2NyZWVuLmh0bWw/cUlEPTU1YThhZjEwNWFhNDEzNDE4ZTZiODk5NSZhaWQ9MjEwNzk1MiIgc2Nyb2xsaW5nPSJubyIgZnJhbWVib3JkZXI9IjAiIHdpZHRoPSIzNTBweCIgaGVpZ2h0PSIzNTBweCIgYWxsb3dmdWxsc2NyZWVuLz4=" frameborder="0" height="370" id="x-ck12-MTU0MjY5NjUzNjI0Mg.." name="238737" src="https://flexbooks.ck12.org/flx/show/interactive/https%3A//www.ck12.org/assessment/tools/geometry-tool/fullscreen.html%3FqID%3D55a8af105aa413418e6b8995%26aid%3D2107952%26hash%3Dac467a8e7d45e05933c3cd6ec8e03260?lang=en" style="max-width: 100%;" title="video" width="370"> </iframe> </div> </div> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h3 id="x-ck12-OTAyYmQ0YjVjMTI4OTkyN2QyMGJjNjBmZDVjYmZmOGY.-7xw"> The Twin Paradox <br/> <span style="color: green; "> ::双双悖论 </span> </h3> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZTE0MGM2ZmUwNzA5MThhMTc5YWFhMGU2MDNhYzRkZjI.-wn2"> Shortly after Einstein proposed the special theory of relativity, an apparent paradox was pointed out. This paradox involved a pair of twins, one of whom traveled away from the earth and returned at very high speeds. The other twin remained at home on earth. Since one twin was traveling at very high speed, time for him was running slower than for the twin who remained on earth. Thus the traveling twin would return home younger than the twin who remained on earth. <br/> <span style="color: green; "> ::爱因斯坦提出相对论特别理论后不久,就出现了明显的矛盾。 这一矛盾涉及到一对双胞胎,其中一对双胞胎离开地球,以极高的速度返回。 另一对双胞胎留在地球上。 由于一对双胞胎以极高的速度旅行,他的时间比留在地球上的双胞胎慢。 因此,旅行的双胞胎比留在地球上的双胞胎年轻。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-MjI1MTViNDEyZGM3MDBmOGYyM2Q4ZDg0NTkwZGY1ZDY.-cch"> The paradox comes about when each twin thinks that their frame of reference was at rest and the other twin’s frame of reference was moving at high speed. Therefore, each twin would find the other one to be younger. The resolution lies in the fact that the traveling twin must accelerate at the beginning and end of the trip and this guarantees that this twin is traveling and his clock is actually running slower. The traveling twin will return home younger than his twin brother. <br/> <span style="color: green; "> ::当每对双胞胎认为他们的参照框架处于休息状态,而另一对双胞胎的参照框架正在高速移动时,就出现了自相矛盾。 因此,每对双胞胎都会发现另一对更年轻。 答案在于旅行的双胞胎必须在旅行的开始和结束时加速,这保证了这对双胞胎正在旅行,而且他的时钟实际上正在减慢。 旅行的双胞胎比他的双胞胎兄弟还年轻。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-MjJkZDJkZDc2MDZiNjk1MjU2MTZhYjViMDYzMjQ4MTM.-gom"> This result was tested in 1971 with a pair of very precise clocks. One clock was sent around the world in high speed jet planes while the matched clock remained at rest. When the traveling clock was returned and placed next to the other clock, the traveling clock <span> showed that </span> less time had passed. <br/> <span style="color: green; "> ::这一结果在1971年用一对非常精确的时钟进行了测试,用高速喷气式飞机向全世界发送了一个时钟,而匹配的时钟仍停留在休息时间。 当旅行时钟被退回并放在另一个时钟旁边时,旅行时钟显示时间已经缩短。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h3 id="x-ck12-ZjFjOGMyNDA4YjQ2MThkNTcyMDIyMDE4NTVlNzJhNTk.-8cn"> Length Contraction <br/> <span style="color: green; "> ::时间长度 缩缩 </span> </h3> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-NjlkNDVjYmEyMTg0ZDJlYjFlYzVmZDZlNWVhNDdhNzY.-6qn"> In a similar manner, an observer on the rocket ship and an observer on the earth will not measure the length of the rocket ship to be the same length in the direction of its motion. The observer on the ship takes out his meter stick and measures the rocket ship to be 15 meters long while the ship sits at rest on the earth. An observer outside the ship, standing on the earth, will also measure the ship to be 15 m with his meter stick. When the rocket ship flies past the earth at a significant fraction of the speed of light, the observer on the ship takes out his meter stick and measures the length of the ship and again finds it to be 15 m. The “stationary” observer on the earth with his meter stick measures the moving rocket ship to be less than 15 m. Just for the sake of clarity, let’s say he measures the rocket ship to be 7.5 meters. <br/> <span style="color: green; "> ::以类似的方式,火箭船观察员和地球观察员将无法测量火箭船的长度与其运动方向的长度相同。船上观察员拔出他的表棍,测量火箭船的长度为15米,而该船在地球休眠时,则测量火箭船的长度为15米。在地球的船外,站在地球的观察者也将测量该船与表棒的长度为15米。当火箭船以光速的相当一部分飞过地球时,船上观察员取出他的表棒,测量船只的长度,再次发现是15米。 " 静止 " 观察者用他的表棒将移动的火箭船测量不到15米。为了清楚起见,让我们说,他将火箭船测量为7.5米。 </span> </p> <p id="x-ck12-ZjZmNjE0MWI5OGMyYTJkNzllNTJkMmRkODQzMGU1YTI.-3ei"> <img alt="A rocket ship with a ruler, labeled to show its length when stationary on Earth." data-aligned="none" data-flx-url="/flx/show/THUMB_POSTCARD/image/user%3AY2sxMnNjaWVuY2VAY2sxMi5vcmc./98045-1370327811-33-89-IntPhysC-25-01-rocketshipstationary_NEW.png" data-imageresourceid="7234832" data-imagetype="inline" data-onerror="null" id="x-ck12-MTAyajd5dzduc3Vj" loading="lazy" onerror="null" src="https://dr282zn36sxxg.cloudfront.net/datastreams/f-d%3A6e790f60289417c31e75ce9867d307a91cb41592ca384e9d19530e3f%2BIMAGE_THUMB_POSTCARD_TINY%2BIMAGE_THUMB_POSTCARD_TINY.1" style="" width="175"/> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-YmNmZmM5Y2E1OGQ4MDE1NWUyZTQxNDBjOWQzNmJiZDY.-sqn"> How is it possible that the two observers measure the same rocket ship to be two different lengths? When the rocket ship is at rest on the earth, the on-ship meter stick and the off-ship meter stick are exactly the same but when the rocket ship flies past the earth at significant fraction of the speed of light, the on-ship meter stick as seen by the on earth observer has shrunk. When the observer on ship says the ship is still 15 m long, the observer on earth says, “Nope, your meter stick has shrunk and so has your ship. The ship now measures 7.5 m long using my meter stick.” The on-ship meter stick shrinks by the same percentage that the ship shrinks. <br/> <span style="color: green; "> ::这两位观察家如何将同一艘火箭船测量成两个不同的长度?当火箭船在地球上休息时,船上测量棒和离船测量棒完全一样,但是当火箭船以光速的相当一部分飞过地球时,地球上观察者所看到的船上测量棒已经缩小。当船上观察家说船上仍然有15米长时,地球上观察家说,“不,你的测量棒已经缩水了,你的船也变短了。现在,该船用我的测量棒测量了7.5米长。” 船上测量棒的收缩比例与船上收缩的比例相同。 </span> </p> <p id="x-ck12-ZjZmNjE0MWI5OGMyYTJkNzllNTJkMmRkODQzMGU1YTI.-xn3"> <img alt="The Rocket'S Perceived Length Contraction When Moving At High Speed." data-aligned="none" data-flx-url="/flx/show/THUMB_POSTCARD/image/user%3AY2sxMnNjaWVuY2VAY2sxMi5vcmc./98045-1370327757-15-64-IntPhysC-25-01-rocketshipmoving_NEW.png" data-imageresourceid="7234831" data-imagetype="inline" data-onerror="null" id="x-ck12-NTZkeXN6NW5iMmk=" loading="lazy" onerror="null" src="https://dr282zn36sxxg.cloudfront.net/datastreams/f-d%3A38776d0cb28598193224cfa286eac53663793f45a084b0a7bdb3141d%2BIMAGE_THUMB_POSTCARD_TINY%2BIMAGE_THUMB_POSTCARD_TINY.1" style="" width="175"/> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-MzI1YWEyYThjY2NmZjY3ODI2OTNmNWI3YzIyNTAxYTM.-qim"> It is important to note that the shortening of the moving object does not produce just a smaller object of the same shape. The object is only shortened in the direction of motion. Therefore, a long, slender rocket ship would NOT become a smaller version of itself, but rather, would become a short, stubby rocket ship. <br/> <span style="color: green; "> ::必须指出,移动物体的缩短不会只产生一个形状相同的较小物体,而只是向运动方向缩短物体。 因此,一条长长的、苗条的火箭船不会成为本身的较小版本,而是会变成一条短短的、短的火箭船。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-YzE0NjI4NGEyYzI0ZDdjYzA2MDg3MmUxMzU5YzU1Nzg.-ebp"> At some point in history, the was known as the Fitzgerald contraction and physicists have been known to quote an applicable limerick. <br/> <span style="color: green; "> ::在历史上的某个时刻, 被称为菲茨杰拉德收缩 物理学家们一直知道 引用一个适用的石灰石。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-M2I0ZGQ4OTVkYzhlNmIxNTc5MmZlOTQzZGJhYmE0Zjk.-ez5"> <em> There once was a young man named Fisk, </em> <br/> <span style="color: green; "> ::曾经有个叫费斯克的年轻人 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-N2EzNmRiM2NiOTVmYTY0ZGJkMWYyODc0OTU5ZDMxYjQ.-jzc"> <em> Whose fencing was exceedingly brisk, </em> <br/> <span style="color: green; "> ::谁的栅栏是极其狂野的, </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZjMzODEwODhkMTExYmQ3NjFjYzJhYWE4NzVmMmVkN2M.-yzd"> <em> So fast was his action, </em> <br/> <span style="color: green; "> ::他的行动如此迅速, </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-MmQ4MjYzNjg4Zjc5NDQ5MDE4MTdlMjFjZGM4N2YyYmU.-cwd"> <em> The Fitzgerald contraction reduced his sword to a disk. </em> <br/> <span style="color: green; "> ::菲茨杰拉德的收缩 将他的剑降为磁盘 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZWMyOWEzYWNjNGNmODg5NjQyZDcwYzRmODU5ZDk5NzA.-fea"> The equation for length contraction is <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="L%3DL_o%5Csqrt%7B1-%5Cfrac%7Bv%5E2%7D%7Bc%5E2%7D%7D"> @$\begin{align*}L=L_o\sqrt{1-\frac{v^2}{c^2}}\end{align*}@$ where @$\begin{align*}L_o\end{align*}@$ is the length measured on the moving body, @$\begin{align*}L \end{align*}@$ is the length measured on the stationary body, @$\begin{align*}v\end{align*}@$ is the relative speed of the reference frames, and @$\begin{align*}c\end{align*}@$ is the speed of light.
::长度缩缩的方程式是 @$\ begin{ align}L=L_o\sqrt{1-\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\在\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\参考\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\参考\\\\\\\\参考\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\参考\\ </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-NjEwMDM3NThhYWM2MmJiM2Y5NzQ0MmJmNmU3NTdjNTQ.-cio"> You can see by analysis of the equation that when the relative velocity is zero, the two lengths are the same, when the relative speed is less than 1000 m/s, the effect is too small to notice, and only when the relative speed is a significant fraction of the speed of light is the contraction measureable. <br/> <span style="color: green; "> ::从对等式的分析可以看出,当相对速度为零时,两个长度相同,当相对速度小于1000米/秒时,效果太小,无法引起注意,只有在相对速度是光速的相当部分时,收缩是可测量的。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h4 id="x-ck12-ZjgwNDAzMjUyMjY4YTk1Zjg0MzVmOGJiNGYzMmI1ZjI.-spo"> <strong> Example <span> 2 </span> </strong> <br/> <span style="color: green; "> ::例2 </span> </h4> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-NjhiYzUxODg4YTYxZTQxOTZmMjc1ODdlM2E2NWE1ODg.-h5b"> A spaceship passes the earth at a speed <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="v%20%3D%200.80%20%5C%20%5Ctext%7Bc%7D"> @$\begin{align*}v = 0.80 \ \text{c}\end{align*}@$ .
::太空船以@$\ begin{ align} v = 0.80\\\ text{c\\\\ end{ leign} $ 的速度穿越地球 。-
What is the length of a meter stick laying on a table in the ship and pointing in the direction of motion of the ship as measured by a person on the ship?
::按船上人员测量,放在船上桌子上指向船只运动方向的计时杆长度是多少? -
What is the length of a meter stick laying on a table in the ship and pointing in the direction of motion of the ship as measured by a person on the earth?
::放置在船上的桌子上,指向由地球上一个人测量的船舶运动方向的计时杆的长度是多少?
-
relative to a person on the ship, the meter stick is at rest and therefore its length is 1.0 m
::与船上人员相对而言,仪表棒处于休息状态,因此长度为1.0米。 -
@$\begin{align*}L=L_o\sqrt{1-\frac{v^2}{c^2}}=(1.0 \ \text{m})\sqrt{1-\frac{(0.80 \ c)^2}{c^2}}=(1.0 \ \text{m})\sqrt{1-0.64}=0.60 \ \text{m}\end{align*}@$
::@ $\ begin{ align}}L=L_ o\ sqrt{ 1 -\ frac{ v\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ </span> </li> </ol> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h3 id="x-ck12-NmYzYmI4ODM5M2NhNWQ3OWZjZGI1MzA3ZTQ2Yzk3ZmE.-ojx"> Relativistic Mass <br/> <span style="color: green; "> ::相对质量 </span> </h3> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-N2Q5NzEwNDI3OTRkMDNhOTlhMThmNTM1MDg3ZWY4ZjA.-fmj"> The three basic mechanical quantities are length, time, and mass. Since length and time have been shown to be relative (their value depends on the reference frame from which they are measured), it might be expected that mass is also relative. Einstein showed that the mass of an object increases as its speed increases according to the formula <br/> <span style="color: green; "> ::3个基本机械基本数量是长度、时间和质量。由于长度和时间被证明是相对的(其价值取决于测量质量的参考框架),因此可以预计质量也是相对的。爱因斯坦表明,一个物体的重量随着速度的上升而增加。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-NDFkMzljYmY2MTE2ZTM5MTg4YzE1NjNlMDRmNjgyNmE.-5mr"> <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-block-math" data-mathmethod="block" data-tex="M%3D%5Cfrac%7Bm_o%7D%7B%5Csqrt%7B1-%5Cfrac%7Bv%5E2%7D%7Bc%5E2%7D%7D%7D"> @$$\begin{align*}M=\frac{m_o}{\sqrt{1-\frac{v^2}{c^2}}}\end{align*}@$$
::@$\ begin{ align} msfrac{ m_ ountsqrt{ 1 -\ frac{ v}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\where @$\begin{align*}M\end{align*}@$ is the mass of the moving body, @$\begin{align*}m_o\end{align*}@$ is the mass of the body at rest (or rest mass), @$\begin{align*}v\end{align*}@$ is the velocity of the body and @$\begin{align*}c\end{align*}@$ is the velocity of light.
::@$\ begin{ align\\ m\ end{ align} $ 是移动体的质量, @ $\ begin{ align\\ m_ o\ end{ align} $ 是休息( 或休息质量) 时身体的质量, @ $\ begin{ align\ v\ end{ align} $ 是身体的速度, @ $\ begin{ align\ c\ end{ align} 是光的速度 。For many years it was conventional to enter the discussion of dynamics through derivation of the relativistic mass and this is probably still the dominant mode in textbooks. More recently, however, it has been increasingly recognized that relativistic mass is a troublesome and dubious concept. Many physicists reject the concept of relativistic mass and oppose teaching the concept. Instead, they prefer to approach relativism through rather than through relativistic mass.
::多年来,通过相对质量的衍生而进入对动态的讨论是传统的,这很可能仍然是教科书中的主要模式。 但是,最近人们日益认识到相对质量是一个麻烦和可疑的概念。 许多物理学家反对相对质量的概念,反对教授这一概念。 相反,他们宁愿通过相对质量而不是通过相对质量来对待相对主义。If momentum is the preferred place to express relativistic dynamics, the equation is
::如果势头是表达相对相对主义动态的首选地方,那么等式就是@$$\begin{align*}p=\frac{m_ov}{\sqrt{1-\frac{v^2}{c^2}}}\end{align*}@$$
::@ $\ begin{ ALIGN} pfrac{ m_ ov_ unsqrt{ 1-\ frac{ v}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ end{ ALign} $Where @$\begin{align*}p\end{align*}@$ is momentum, @$\begin{align*}m_o\end{align*}@$ is rest mass, @$\begin{align*}v\end{align*}@$ is the velocity of the body and @$\begin{align*}c\end{align*}@$ is the velocity of light.
::@ $\ begin{ align\ p\ end{ align} $ 是动力, @ $\ begin{ align\\ m_ o\ end{ align} $ 是休息质量, @ $\ begin{ align\ end{ align\ end} $ 是身体的速度, @ $\ begin{ align\ c\ end{ align\ $ 是光的速度 。 </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h4 id="x-ck12-NTg5MmJkNDI2YWU5MTI4MDI2NGIzMGU5MmIxNzQ5MmY.-6x8"> <strong> Example <span> 3 </span> </strong> <br/> <span style="color: green; "> ::例3 </span> </h4> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-MjEwZmEzNzhhNGVmMDQzYzA4MjFhN2U2ODRhZGUzOWE.-ywo"> An <span class="x-ck12-vocab-interlink" data-definition="negatively%20charged%20subatomic%20particle%20that%20orbits%20the%20nucleus." data-id="6301" data-interlink-id="x-ck12-86je61qpd4rzkyqe" data-json="eyJkYXRhLXN5bWJvbCI6ICI8bWF0aD5lXnstfTwvbWF0aD4iLCAiZGF0YS1wbHVyYWwiOiAiIiwgImRhdGEtZGVmaW5pdGlvbiI6ICJuZWdhdGl2ZWx5JTIwY2hhcmdlZCUyMHN1YmF0b21pYyUyMHBhcnRpY2xlJTIwdGhhdCUyMG9yYml0cyUyMHRoZSUyMG51Y2xldXMuIiwgImRhdGEtaWQiOiA2MzAxLCAiZGF0YS1sYW5ndWFnZUlEIjogMSwgImRhdGEtdGVybSI6ICJlbGVjdHJvbiJ9" data-languageid="1" data-plural="" data-symbol="@$e^{-}@$" data-term="electron" role="term" tabindex="0"> electron has a rest mass of @$\begin{align*}9.1 \times 10^{-31} \ \text{kg}\end{align*}@$ . If the electron were traveling at 0.50 c relative to an observer, what electron mass would the observer measure?
::电子的休息质量为 @ $\ begin{ align\\\ 9. 1\ times 10\\\\ 31}\\\ text{ kg\\\ end{ align\ $. 如果电子相对于观察者以0. 50 c 的速度旅行, 观察者将测量电子质量多少? </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-xsy"> <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="M%3D%5Cfrac%7Bm_o%7D%7B%5Csqrt%7B1-%5Cfrac%7Bv%5E2%7D%7Bc%5E2%7D%7D%7D%3D%5Cfrac%7B9.1%20%5Ctimes%2010%5E%7B-31%7D%20%5C%20%5Ctext%7Bkg%7D%7D%7B%5Csqrt%7B1-%5Cfrac%7B(0.50%20%5C%20c)%5E2%7D%7Bc%5E2%7D%7D%7D%3D%5Cfrac%7B9.1%20%5Ctimes%2010%5E%7B-31%7D%20%5C%20%5Ctext%7Bkg%7D%7D%7B%5Csqrt%7B1-0.25%7D%7D%3D1.1%20%5Ctimes%2010%5E%7B-30%7D%20%5C%20%5Ctext%7Bkg%7D%20"> @$\begin{align*}M=\frac{m_o}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{9.1 \times 10^{-31} \ \text{kg}}{\sqrt{1-\frac{(0.50 \ c)^2}{c^2}}}=\frac{9.1 \times 10^{-31} \ \text{kg}}{\sqrt{1-0.25}}=1.1 \times 10^{-30} \ \text{kg} \end{align*}@$
::@ $\ begin{ align}M\\\\ frac{ m_ ounsqrt{ 1\\ frac{ v\\\ 2\\\ 2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h3 id="x-ck12-YmIxMzdhN2MzZmQ2ZjA1NWU2ZDI3YTQ5NzAwMGE0ZDA.-xp0"> The Ultimate Speed Limit <br/> <span style="color: green; "> ::终极速度限制 </span> </h3> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZjdhYmE1Y2NiNGE3ZDFkYjEzZTcxNWQzMTllOTE5ZDE.-9cf"> A result of the special theory of relativity is that no physical object can equal or exceed the speed of light. From the equation for relativistic mass, it can be seen that as the object is accelerated faster and faster, its mass becomes greater and greater. The greater mass would require an even greater force to accelerate it. If the velocity of the mass ever reached the speed of light, the denominator of the equation would become zero and the mass would become infinite. The energy required to accelerate an infinite mass would also be infinite. The fact that light itself travels at the speed <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="c"> @$\begin{align*}c\end{align*}@$ , implies that light has a zero rest mass. Of course, light is never at rest.
::相对论特殊理论的结果是,任何物理物体都不能等同或超过光速。 从相对质量的方程式中可以看出,当物体加速速度加快,质量就会越来越快。 更大的质量需要更大的力量来加速它。 如果质量速度达到光速, 方程式的分母就会变成零, 质量就会变得无限。 加速无限质量所需的能量也会是无限的。 光本身以@ $\ begin{ alignc\\ end{ align} $ 的速度行走, 意味着光有零的休息质量。 当然, 光从不处于休息状态 。The Equivalence of Mass and Energy
::质量和能源等同The special theory of relativity is also the origin of Einstein’s most famous equation, @$\begin{align*}E = mc^2\end{align*}@$ , and the concept that mass and energy are different forms of the same thing. Einstein himself described the equivalence of mass and energy as the “most important upshot of the special theory of relativity”. The idea is not that mass and energy can be mathematically related but that they two are, in fact, simply different forms of the same thing. Each may be converted into the other and the conversion factor is the speed of light squared. Launch the PLIX Interactive below to further explore mass-energy equivalence:
::相对论的特殊理论也是爱因斯坦最著名的方程式的起源,即@$\ begin{align}E = mc\2\end{align}$,以及质量和能源是同一事物不同形式的概念。爱因斯坦自己将质量和能源的等值描述为“相对论特别理论的最重要结果 ” 。 思想不是质量和能源可以在数学上相联,而是两者实际上只是同一事物的不同形式。每种形式都可以转换为另一种形式,而转换系数是光的正方形速度。启动下面的PLIX互动来进一步探索质量能源等值:Example 4
::例4How much energy would be released if a @$\begin{align*}\pi\end{align*}@$ meson @$\begin{align*}(\text{rest mass}= 2.4 \times 10^{-28} \ \text{kg})\end{align*}@$ was transformed by decay completely into energy?
::如果一个@ $\ begin{ align\ pi\ end{ align} $ meson @ $\ begin{ align} (\ text{ rest mass}\ 2. 4\ times 10\\\ 28}\\\ text{kg})\ end{ align}$ 被完全衰变成能量, 将会释放多少能量?@$\begin{align*}E = mc^2 = (2.4 \times 10^{-28} \ \text{kg})(3.0 \times 10^8 \ \text{m/s})^2 = 2.2 \times 10^{-11} \ \text{joules}\end{align*}@$
::@ $\ begin{ align} @ E = mc} 2 = (2.4\ times 10\\ 28}\\ text{kg} (3. 0\ text} 10\ 8\\\ text{ m/ s} = 2. 2\times 10\\\\ 11}\\ text{joules}end{align}\\\ text{ </span> </p> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <h3 id="x-ck12-YmQ3ZDFlOGZjZDY3ODBlNzdlYjkwZmMxZjllZDQ4Y2E.-d6i"> The Impact of the Theory of Special Relativity <br/> <span style="color: green; "> ::特别相对论理论的影响 </span> </h3> <button class="play-button btn btn-success" style="float: right;" value="@s"> 播放段落 </button> <p id="x-ck12-ZjE5OGY2ZGUyNTAxNGI0YTM3ODMyOWEwYjA0OGRjN2Q.-c9x"> A great many experiments have been performed to test the predictions of special relativity. No contradictions have been found. Scientists have therefore accepted special relativity as an accurate description of nature. When the relative velocities of objects are considerably less than the speed of light, the formulas for relativistic time, length, and mass all reduce to the classical formulas. It is required that the two theories correspond where they overlap at speeds much less than <span class="x-ck12-mathEditor" data-contenteditable="false" data-edithtml="" data-math-class="x-ck12-math" data-mathmethod="inline" data-tex="c"> @$\begin{align*}c\end{align*}@$ . Special relativity does not contradict classical mechanics. Rather, it is a more general theory needed for object speeds approaching the speed of light.
::为了测试对特殊相对论的预测,已经进行了大量实验,没有发现矛盾。因此,科学家接受了特殊的相对论作为自然的准确描述。当天体相对速度大大低于光速时,相对时间、长度和质量的公式都缩小到古典公式。要求这两个理论在速度上与速度相重叠的地方相对应,速度小于@$\begin{align\c\end{align}c\end{align}$。特殊相对论并不与古典力相矛盾。相反,它是接近光速的天体速度所需要的一种更为一般性的理论。Further Reading
::继续阅读Summary
::摘要-
The special theory of relativity essentially explains how to interpret motion between different inertial frames of reference, that is, places that are moving at constant speeds relative to each other.
::相对论特别理论基本上解释了如何解释不同惯性参照框架之间的运动,即以相对同步速度移动的地方。 -
Special relativity is based on two postulates:
-
The laws of physics are the same for all observers within their own inertial reference frame.
::所有观察者在其惯性参照框架内的物理定律都是一样的。 -
The speed of light in a vacuum is the same for all observers regardless of their relative motion or the motion of the source of the light.
::真空中的光速对所有观察者都是一样的,无论其相对运动或光源运动如何。
::特殊相对论基于两个假设:物理学法则对所有观察者在自己的惯性参照框架内都是一样的,所有观察者不论相对运动或光源运动,在真空中的光速都是一样的。 -
The laws of physics are the same for all observers within their own inertial reference frame.
-
The special theory of relativity explains the unchangeable speed of light better than classical mechanics, but it also has some surprising consequences. For example, according to the theory of special relativity,
-
Two events that occurred simultaneously for one observer were not simultaneous for another observer if the two observers had relative motion to each other. (Relativity of simultaneity).
::一个观察员同时发生的两起事件,如果两个观察员相对地相互移动,对另一个观察员来说不是同时发生的。 (同时的相对性)。 -
Clocks in a moving frame of reference tick more slowly than an observer’s “stationary” clock. (Time dilation).
::移动参考框架的时钟比观察者的 " 静止 " 时钟慢。 (时间放大) -
Objects are measured to be shorter in the direction that they are moving with respect to a stationary observer. (Length contraction).
::物体相对于固定观察员而言,其移动方向被测量为较短。 (活度收缩)。 -
The mass of a moving object will be greater as measured by an observer at rest.
::移动对象的质量将按休息时的观察者所测量的更大。 -
@$\begin{align*}E = mc^2\end{align*}@$
, energy and mass are equivalent and transmutable. (Mass-energy equivalence).
::@$\ begin{ align}E = mc_ 2\ end{ end{ align}$, 能量和质量是等效和可变的 。 ( Mass- energy equality) -
No physical object can travel faster than the speed of light in a vacuum. (Maximum speed is finite).
::在真空中,任何物理物体的飞行速度都不能比光速快。 (最大速度是有限的)。
::相对论的特殊理论解释光的不可改变速度比古典力学更好,但也有一些令人惊讶的后果。例如,根据特殊相对论理论,如果两个观察者彼此相对运动,一个观察者同时发生的两个事件对另一个观察者来说并不是同时发生的。(同时性的相对性)。在移动参照框架中的时钟比观察者的 " 静止 " 时钟要慢得多。物体在固定观察者移动的方向上被测量为更短。 (Length收缩) 。移动对象的质量会比在休息时的观察者所测量的要大。 @$\ begin{align}E= mc%2\end{align}{align}$,能量和质量是等同和可移动的。 (Mass-egal) 没有物理物体可以比真空中的光速更快移动。 (最大速度是有限的)。 -
Two events that occurred simultaneously for one observer were not simultaneous for another observer if the two observers had relative motion to each other. (Relativity of simultaneity).
Review
::回顾-
A woman stands on top of a moving railroad car and tosses a ball straight up in the air. If there is no air resistance, where will the ball come back down?
-
behind the railroad car
::火车车后面 -
ahead of the railroad car
::火车车前面 -
into the woman’s hand
::进入女人的手中
::一位女士站在一辆移动的铁路车顶上,将球扔在空中。 如果没有空气阻力,球会从哪回来? 在铁路车前面的铁路车后面,球会落到哪个女人手里? -
behind the railroad car
-
If you were inside a windowless car that was traveling perfectly smoothly at a constant velocity, you could determine the speed of the car by dropping a ball.
-
True
::真实 -
False
::假假
::如果你在一辆没有窗户的汽车里, 它以恒定速度顺利运行, 你可以通过投球来决定车速。 真的假的。 -
True
-
Does time dilation mean that time actually passes more slowly in a moving reference frame or that it only seems to pass more slowly?
::时间推算是否意味着在移动的参照框架中,时间的通过实际上比较缓慢,还是似乎只是过得比较缓慢? -
A young looking woman astronaut has just arrived home from a long trip at near the speed of light. She rushes up to an old gray-haired man and refers to him as her son. Is this possible?
::一位年轻的女宇航员刚从长途跋涉中 以接近光速回到家 她冲向一个灰色头发的老男人 称他为她的儿子 有可能吗? -
If you were traveling away from the earth at a speed of 0.5 c, how would your heartbeat, length, and mass change? What would observers from earth say about their measurements of your heartbeat, length, and mass?
::如果你以0.5厘米的速度离开地球,你的心跳、长度和质量会如何变化?来自地球的观察家会怎么说他们衡量你的心跳、长度和质量? -
A person on another planet shines a flashlight at you. The planet and the earth are both in the same reference frame and are not moving relative to each other. At the same instant that the person shined the flashlight at you, a person on a spaceship passing that planet and moving toward you at 0.5 c also shined a flashlight at you. Which light pulse will reach you first?
-
the light from the person on the planet
::从地球上的人发出的光 -
the light from the flashlight on the spaceship
::宇宙飞船上的手电筒发出的光芒 -
the two light pulses will reach you at the same time
::两个光脉冲会同时到达你
::在另一个星球上,一个人在另一个星球上朝你闪闪闪光光。 行星和地球都处于同一个参照框架之中, 并且没有相互相对移动。 与此同时, 那个人将闪光光照在你身上, 一个人在通过这个星球的飞船上, 一个人在0. 5 c 时朝你移动, 另一行星上的人也将闪光光照在你身上。 哪个光脉冲会先到达你身上? 地球的人发出的光, 宇宙飞船上闪光发出的光, 两个光脉冲会同时到达你身上。 -
the light from the person on the planet
-
If a spaceship will shrink when it travels at a speed of 0.75 c, do we need to make design changes to accommodate passengers and crew?
::如果一艘飞船在以0.75c的速度飞行时会萎缩,我们是否需要修改设计,以容纳乘客和机组人员? -
A beam of particles travel at a speed of
@$\begin{align*}2.85 \times 10^8 \ \text{m/s}\end{align*}@$
. At this speed, the particles average lifetime is measured to be
@$\begin{align*}2.50 \times 10^{-8} \ \text{s}\end{align*}@$
. What is a particle’s lifetime when they are at rest?
::粒子移动速度为 @ $\ begin{ align}\ 2. 85\ times 10\ 8\\\ text{ m/ s\\\\\ end{ align} $ 。 如此速度, 粒子的平均寿命被测量为 @ $\ begin{ align} 2. 50\ times 10\\\\ 8}\\ text{ s\\ end{ align} $。 当粒子休息时, 粒子的寿命是什么 ? -
A spaceship passes you at a speed of 0.80 c. You measure its length to be 90.0 m. How long would this space ship be at rest?
::宇宙飞船以0.80 c.的速率通过您。您测量其长度为90.00 m. 这艘宇宙飞船需要休息多久? -
If you were to travel to a planet 36 light years from earth at a speed of 0.98 c, what would you measure the distance to be?
::如果你去一个36光年的星球 以0.98c的速度从地球飞到一个36光年的星球 你会测量到什么距离? -
If the rest mass of a proton is
@$\begin{align*}1.67 \times 10^{-27} \ \text{kg}\end{align*}@$
, what is its mass when traveling at 0.85 c?
::如果质子的其余质量是 @$\ begin{ align\\\ 1. 67\ times 10\\\\ 27}\\ text{kg\\ end{ align}$, 以0. 85 c 乘车时的质量是多少? -
At what speed will the relativistic mass of an object be exactly double its rest mass?
::物体的相对相对质量究竟会是其休息质量的两倍,速度是多少? -
How much energy would be produced if 1.00 milligram of mass were completely converted into energy?
::如果将1 000毫克质量完全转化为能源,将会产生多少能源?
Explore More
::探索更多Use this resource to answer the questions that follow.
::使用此资源回答下面的问题 。-
What is relative motion?
::什么是相对运动? -
The speed of light is a ___________ across the universe. What letter represents this?
::光速是宇宙的 ° 。 哪个字母代表这个 ? -
To maintain a uniform speed of light, does the behavior of
space
or time change? Why?
::为了保持统一的光速, 空间或时间的行为会改变吗? 为什么?
-
The laws of physics are the same for all observers within their own inertial
reference frame
.