章节大纲

  • On a road trip, you stop at a vending machine during a lunch break. Each item in the vending machine has a unique code that consists of a letter followed by a number. Is the vending machine an example of a function ?
    ::在一次公路旅行中,您在午餐休息期间在自动售货机停靠一个自动售货机。自动售货机中的每件物品都有一个独特的代码,由字母和数字组成。自动售货机是功能的示例吗?

    We explore what makes a relationship between an input and an output a function in this section.
    ::我们探讨本节中投入与产出之间何以关系,何以将产出与产出作为职能。

    lesson content

    Forms of Relations
    ::关系形式

    A  relation  is a correspondence between elements in one set and elements in another set . Loosely, it expresses a relationship between the two sets. That relationship can take many forms. Let's consider some examples.
    ::一种关系是一组元素和另一组元素之间的对应关系。 粗略地说, 它表示两组元素之间的关系。 这种关系可以有多种形式。 让我们来考虑一些例子 。

    A.  Table of Values: A table of values expresses a relationship between a set of input values and a set of output values. For example, 
    ::A. 数值表:数值表表示一组输入值与一组输出值之间的关系。例如,

    1.

    President Number
    Barack Obama 44
    George W. Bush 43
    Bill Clinton 42

    In this relation , each president corresponds to a number indicating the order that they served in office 1 . 
    ::在这方面,每位总统对应一个数字,表示他们任职的顺序1。

    2.

    x y
    1 9
    2 10
    3 12

    In this relation, 1 corresponds with 9, 2 corresponds with 10, and 3 corresponds with 12.  
    ::在这方面,1对应9,2对应10,3对应12。

    B. Set of Ordered Pairs:  A set of ordered pairs is another form of a relation. In the first set, black corresponds with 1, and in the second set, -4 corresponds with 1.
    ::B. 一组有秩序对等:一组有秩序对等是另一种关系形式。在第一组中,黑色对1,第二组中,黑色对1。

    1.   { ( blue , − 2 ) , ( red , − 5 ) , ( white , − 2 ) , ( black , 1 ) } 2.   { ( − 4 , 1 ) , ( 0 , 3 ) , ( 0 , 0 ) , ( 6 , − 7 ) }

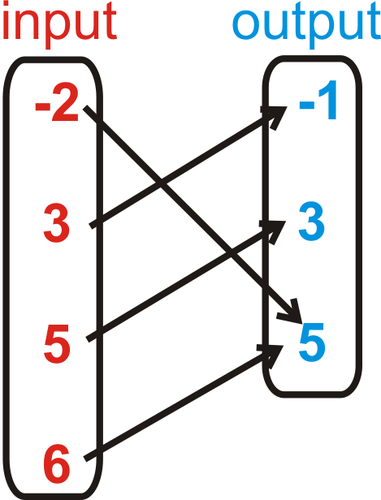
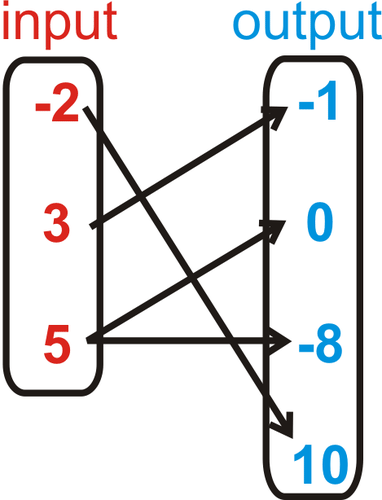
    ::1. {(蓝色,-2),(红色,-5),(白,-2),(黑,1)}2.{{(-4,1,(0,3),(0,),(6,-7)}

    C. Picture: A picture that uses ovals to represent the sets of inputs and outputs and arrows to represent the mapping between them is an example of a relation. For example, the two pictures below are relations.
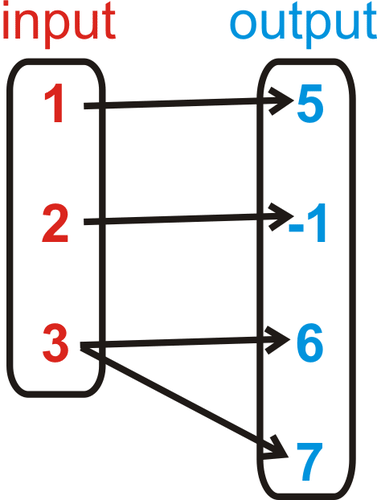
    ::C. 图片:一张使用 ovals 代表输入和输出集的图片和箭头代表它们之间绘图的箭头是关系的一个实例。例如,下面的两幅图片是关系。

    The arrows indicate what each of the inputs corresponds to. 
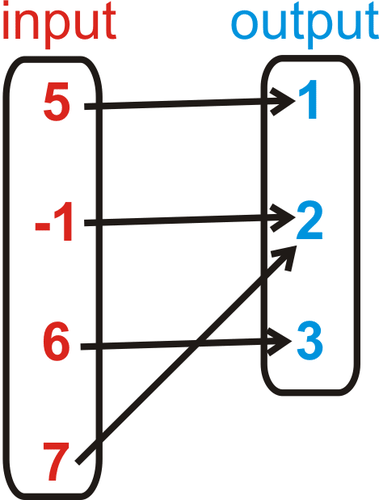
    ::箭头表示每个输入对应的输入。

    1.                                                       2.

    lesson content

                   lesson content

    D. Graphs: Any graph represents a relation between an input and an output.
    ::D. 图:任何图表都表示输入和输出之间的关系。

    1. For example, the graph (in statistics, a graph like this is called a scatter plot) below shows the relationship between the input, length of time Old Faithful erupts (the geyser in the image below), and the output or time between eruptions 2 . 
    ::1. 例如,下面的图表(在统计学中,像这样的图表称为散射图)显示了输入、时间长度、旧的信仰喷发(以下图像中的喷发玻璃)和喷发之间的输出或时间之间的关系。

     

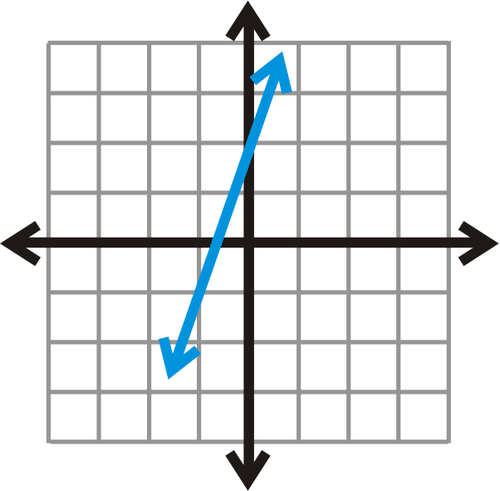
    2. Graphs, like this graph of a line, are relations too. By finding the coordinates of an ordered pair , we can find the correspondence between an input, or  x -value, and an output, or y- value.  
    ::2. 图表与线条图一样,也是一种关系。通过找到定购一对的坐标,我们可以找到输入、x值、输出或y值之间的对应关系。

    lesson content

    E. Words: You can express a relation between an input and an output with a description. 
    ::E. 单词:您可以表达输入和带有描述的输出之间的关系。

    1. Name the siblings of a student. Here each student corresponds to the names of their siblings.
      ::给学生的兄弟姐妹取名。这里每个学生的名字与其兄弟姐妹的名字相对应。
    2. The output is 3 more than the square of the input.
      ::输出比输入的平方多3个。

    F. Formulas:  This is probably one of the most common ways to express a relation. We have considered relations in previous chapters.
    ::F. 公式:这可能是表达关系的最常见方式之一,我们在前几章中考虑了各种关系。

    1.   y = 2 x − 5 2.   y ≤ 2 x − 5

    ::1. y=2x-52.y=5

    Both of these express a relationship between the inputs, x -values, and the outputs, y -values. 
    ::两者都表示投入、x值和产出、y值之间的关系。

    Functions
    ::职能职能职能职能职能职能职能职能职能职能职能职能职能职能职能

    There are special types of relations called functions. A function is a relation where there is exactly one output for every input. In other words, a relation is not a function if at least one input value has more than one output value. 
    ::存在被称为函数的特殊类型关系。 函数是指每个输入都有一个输出的关联。 换句话说, 如果至少一个输入值有一个以上的输出值, 则关系不是函数 。

    An example of a function is the vending machine example in the introduction (assuming the machine has been loaded properly). You type in a code and that code corresponds to one output or, in this case, snack. Let's identify the functions from the examples above.  
    ::函数的一个实例是导言中的自动售货机示例(假设机器已正确装入)。您在代码中键入一个代码,该代码对应一个输出,或者在此情况下对应零食。让我们从以上示例中找出函数 。

    Example 1
    ::例1

    Identify which relations above are functions. 
    ::确定上述哪些关系是职能。

    Solution:  
    ::解决方案 :

    A. Tables: Both of these tables represent functions.
    ::A. 表:这两个表格代表职能。

    1. Each president listed corresponds to only one number to indicate the order he served in office. (This would not be a function if we included Grover Cleveland, who was the 22nd and 24th president of the United States). 1  
    ::1. 名单上的每个总统只有一个数字表示他任职的次序。 (如果我们包括格罗夫·克利夫兰,他就是美国第22和第24任总统,那么这不是一项职能)。 1

    2. Each input—1,2, and 3—corresponds to only one output. 
    ::2. 每项投入——1、2和3——只对应一项产出。

    by CK-12 demonstrates how to determine if a relation is a function from a table of input and output values.  
    ::CK-12 显示如何从输入和输出值表确定关系是否函数。

     

    B. Ordered Pairs
    ::B. 有序对等

    1. Each color only corresponds to one number. This is a function. 
    ::1. 每个颜色只对应一个数字。这是一个函数。

    2. This is not a function. Zero corresponds to 3 and to 0. It has two outputs. This is only a relation.
    ::2. 这不是一项职能。 零等于3和0。 它有两个产出,这只是一种关系。

    by CK-12 explains the difference between a relation and a function.  
    ::CK-12 解释关系和函数的区别。

     

    C. Pictures
    ::C. 图片

    1. Since 3 corresponds to two outputs, 6 and 7, this is not a function. 
    ::1. 由于3项是两项产出,即6项和7项产出,因此这不是一项职能。

    2. Each input in this picture corresponds to a unique output. It is a function.
    ::2. 本图中的每项输入都对应一个独特的产出。这是一个函数。

    by KiwiChan0 demonstrates how to distinguish between relations and functions.
    ::KiwiChan0展示了如何区分关系和职能。

     

    D. Graphs
    ::D. 图图

    1. This scatter plot is not a function since many of the inputs correspond to multiple outputs. For example, an eruption of 3.5 minutes corresponds to a few wait times between 70 and 80 minutes.
    ::1. 散射图不是一个函数,因为许多输入与多个输出相对应,例如,3.5分钟的喷发相当于70至80分钟的几次等待。

    2. The line is a function since each x -value only corresponds to one y -value.  
    ::2. 该直线是一个函数,因为每个x值只对应一个y值。

    E. Words
    ::E. 词词

    1. Unless each student has only one sibling or no siblings, this is not a function. For example, if Suzanne has two brothers, then she corresponds to two outputs.
    ::1. 除非每个学生只有一个兄弟姐妹或没有兄弟姐妹,否则这不是一项职能,例如,如果Suzanne有两个兄弟,那么她就相当于两项产出。

    2. Each input has a unique output. For example, if the input is 1, we square it and add 3, and only output 4. This is a function.
    ::2. 每个输入都有独特的输出,例如,如果输入为1,我们方形,增加3,只有产出4,这是一个函数。

    F.  Formulas
    ::F. 公式

    1. The linear equation is a function. If you put in a value for x , you will only get one value for  y . 
    ::1. 线性方程式是一个函数。如果将 x 的值放入一个数值,y 只有一个数值。

    2. The linear inequality is not a function. If you choose a value for  x , there are many values for  y that will satisfy the inequality.

    ::2. 线性不平等不是一个函数。如果选择 x 值,y 值有许多可以满足不平等的值。

       WARNING
    ::警告

    A function can have repeated  y -values.
    ::函数可重复 Y 值。

    For example,  y = 6  is a function. 
    ::例如,y=6是一个函数。

    x = 1   only corresponds to 6
    ::x=1 仅对应于 6

    x = 2   only corresponds to 6
    ::x=2 仅对应于 6

    x = 3   only corresponds to 6
    ::x=3 仅对应于 6

    Any  x -value only corresponds to 6. Six is the unique output. 
    ::任何 X 值仅对应于 6. 6, 6 是独有的输出 。

    Feature: Couch Potato
    ::特色:土豆土包子

    by Meredith Beaton
    ::梅雷迪思·贝顿(签名)

    The television has been available to most consumers since the 1920s. In 2009, 78% of households had at least one television. Television broadcasts (and television accessed through the internet) are the primary way that people receive information in their homes, whether it is news, entertainment, or sports, TV allows people to connect to the world.
    ::自20世纪20年代以来,大多数消费者都可以收看电视。 2009年,78%的家庭至少有一台电视。 电视广播(以及通过互联网收看的电视)是人们在家中获得信息的主要方式,无论是新闻、娱乐还是体育、电视都允许人们与世界连接。

    Televisions receive radio waves that are broadcast on specific channels (54 - 890 MHz frequency). Radio waves are a type of electromagnetic wave, similar to those that cook food in a microwave. Electromagnetic waves can be measured by their wavelength (the distance between the peak of two waves). Radio waves have a wavelength roughly the size of a football field. These travel through the air to reach your television and your television converts the energy from the waves into a picture on your TV screen.
    ::无线电波是一种电磁波,类似于在微波中烹饪食物的电磁波。电磁波可以用波长(两波峰之间的距离)来测量。无线电波的波长大约是足球场的大小。这些波的波长大约是足球场的大小。这些波程通过空气进入电视,电视将波的能量从波变成电视屏幕上的图片。

    Electromagnetic waves can also be described by their energy and frequency. These two descriptors along with wavelength can all be related mathematically and easily described on a graph, like the transverse wave graph above. Is the relationship shown on the graph a function?
    ::电磁波也可以用它们的能量和频率来描述。 这两种描述器和波长都可以在数学上和图上轻松描述, 如上面的反向波图。 图表上显示的关系是函数吗 ?

    by   Best0fScience describes radio waves in more detail.
    ::Best0fScience更详细地描述了无线电波。

     

    Summary
    ::摘要

    • Relations can be expressed in various forms.
      ::关系可以各种形式表达。
    • Functions are relations where each output corresponds to a unique input.
      ::功能是指每项产出与独特投入相对应的关系。

    Review
    ::回顾

    Determine if the following relations are functions. Briefly explain your answer.
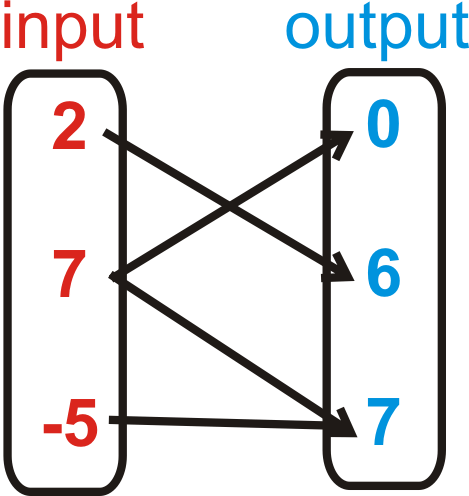
    ::确定以下关系是否为函数。 简要解释您的答复 。

    1. 

    x y
    1 3
    -1 -3
    2 5
    -2 -5

    2. 

    x y
    -5 7
    -4 7
    -3 1
    -4 1

    3. {(3, -5), (8, 1), (-3, -3), (5, 1)}

    4. {(9, -2), (0, 0), (7, 4), (9, 3)}

    5. {(-9, -10), (4, -5), (6, -5), (4, -10)}

     6.

      lesson content

    7.

    lesson content

          

    8.

    lesson content

     

    9. Given a student, identify what street they live on.
    ::9. 对于学生,请指明他们住在哪条街上。

    10.  y = x 2  (Assume  x  is the independent variable.)
    ::10. y=x2(Assume x 是独立的变量。 )

    11.  x = y 2  (Assume  x  is the independent variable.)
    ::11. x=y2 (Assume x 是独立的变量 。)

    Explore More
    ::探索更多

    1. Determine whether the relation of a student to their algebra instructor is a function. What about the relation of an algebra instructor to their students?
    ::1. 确定学生与其代数教官的关系是否是一种功能。代数教官与学生的关系如何?

    2. Determine whether the relation of a household income to their tax rate is a function. What about the relation of the tax rate to a household income?
    ::2. 确定家庭收入与其税率的关系是否是一种职能。税率与家庭收入的关系如何?

    3. A function is one-to-one if each y -value corresponds to a different x -value. Does a function have to be one-to-one? Explain.
    ::3. 如果每个y值对应不同的x值,则函数为一对一。函数必须一对一吗?解释。

    4. A function is onto if every y -value corresponds to an x -value. Does a function have to be onto? Explain.
    ::4. 如果每个 Y 值与 x 值对应,函数即为对应。函数是否必须对应?解释。

    Answers for Review and Explore More Problems
    ::回顾和探讨更多问题的答复

    Please see the Appendix.
    ::请参看附录。

    Reference
    ::参考参考参考参考参考文献

    1. "US Presidents List," last accessed May 22, 2017, https://www.presidentsusa.net/presvplist.html.
    ::1. “美国总统名单”,2017年5月22日最后一次查阅,https://www.presidentsusa.net/presvplist.html。

    2. "Old Faithful," last edited May 17, 2017, https://en.wikipedia.org/wiki/Old_Faithful.
    ::2017年5月17日编辑, https://en.wikipedia. org/wiki/Old_Faithful.