节: 赤道不平等 | 8.9 严重不平等

章节大纲

A lot of data is generated during athletic competitions—for example, a baseball player's on-base plus slugging (OPS) ¹ , a statistic calculated as the sum of the player's on-base percentage and slugging average. Over a baseball player's career, his OPS is likely to fluctuate. There is an initial period where he has good physical abilities, but is hampered by inexperience. Then, in the middle of his career, he has good physical skills and more experience. Finally, towards the end of his career, he has good experience, but his physical abilities decline. Therefore , we could model a player's OPS over a career as a quadratic function . Suppose we wanted to determine when a player's OPS is predicted to be above (or greater than) a certain value. To solve this problem, we would need to solve a quadratic inequality . In this section we will explore how to solve quadratic inequalities both graphically and algebraically.
::体育比赛中产生了许多数据,例如棒球运动员在基地上加上打拳(OPS)1, 计算为球员在基地上的百分比和打拳平均数之和的统计数字。在棒球运动员的职业生涯中,他的OPS很可能会波动。在初期,他有良好的体能,但受到经验不足的阻碍。然后,在职业生涯的中间,他有良好的体能和更多的经验。最后,在职业生涯结束时,他有良好的经验,但体能下降。因此,我们可以将球员的OPS模拟成一个职业,作为二次函数。假设我们想确定一个球员的OPS预计何时会超过(或大于)一定价值。为了解决这个问题,我们需要解决四极不平等问题。在这一部分,我们将探索如何以图形和代数方式解决四极不平等问题。

lesson content

Quadratic Inequalities
::赤道不平等

Previously, we covered linear inequalities in two variables. Our 1st step in graphing a linear inequality was to graph the boundary line , or the linear equation . Quadratic inequalities are similar. Our 1st step will be to solve the quadratic equation .
::此前,我们在两个变量中涵盖了线性不平等。我们绘制线性不平等图的第一个步骤是绘制边界线或线性方程。二次曲线不平等相似。我们的第一个步骤是解决二次方程。

How To Solve a Quadratic Inequality
::如何解决赤道不平等问题

1. Arrange the terms so that one side of the inequality is equal to 0, i.e., $\begin{align*}ax^2+bx+c>0, ax^2+bx+c \ge 0, ax^2+bx+c <0, \ \text{or} \ ax^2+bx+c \le 0.\end{align*}$
::1. 排列术语,使不平等的一方等于0,即x2+bx+c>0,ax2+bx+c+c=0,ax2+bx+c=0,ax2+bx+c=0,或x2+bx+c=0。

2. Solve the quadratic equation, $\begin{align*}ax^2+bx+c=0\end{align*}$ .
::2. 解决四方方程式,Ax2+bx+c=0。

Graphical Approach
::图形图形化方法

3. Determine if the parabola opens upward $\begin{align*}(a > 0)\end{align*}$ or downward $\begin{align*}(a < 0)\end{align*}$ .
::3. 确定抛物线是向上(a>0)还是向下(a<0)打开。

4. Sketch a graph of the parabola using the solutions from step 2 and the information from step 3.
::4. 用第2步的解决方案和第3步的信息绘制一个抛物线图。

5. Read the sketch to determine for which x- values the corresponding y -values satisfy the inequality.
::5. 阅读草图以确定相应的Y值的X值能满足不平等。

Algebraic Approach
::代数法

3. The solutions to the quadratic equation will divide the real number line into intervals:
::3. 二次等式的解决方案将把实际数字线按间隔划分:

2 real solutions: There will be three separate intervals.
::2个实际解决办法:将分3个不同的间隔。

1 real solution: There will be two separate intervals.
::1个实际解决办法:将有两个不同的间隔。

No real solutions: There is one interval to consider—the entire real number line.
::没有真正的解决办法:有一个间隙需要考虑——整个实际数字线。

4. Choose a test point in each interval.
::4. 在每一间隔中选择一个试验点。

5. Substitute each test point in the inequality. If the test point makes the inequality true, then the interval is included in the solution. If the test point does not make the inequality true, then the interval is not included in the solution.
::5. 取代不平等的每个试验点:如果试验点确定不平等是真实的,那么在解决办法中包括间隔;如果试验点没有确定不平等是真实的,那么在解决办法中不包括间隔。

We can use a similar approach for polynomial inequalities and rational inequalities.
::我们可以对多元不平等和合理不平等采取类似办法。

Example 1
::例1

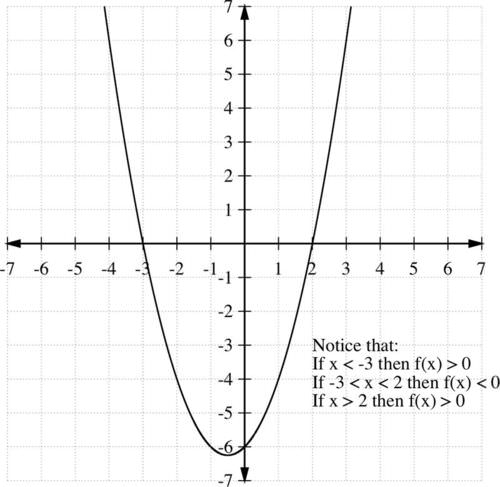
Solve $\begin{align*}x^2+x>6\end{align*}$ graphically.
::以图形方式解决 x2+x>6 。

Solution: First we need to get all the terms to one side. Next we need to set the left side equal to zero, and solve for x. This will tell us the x - intercepts for the graph of our quadratic inequality.
::解决方案: 首先我们需要将所有条件都放到一边。下一步我们需要将左侧设置为零, 并解决 x。这将告诉我们我们二次不平等图的 X 界面。

\begin{aligned} x^{2} + x > 6 \\ \underline{- 6 - 6} \\ x^{2} + x - 6 > 0 \\ x^{2} + x - 6 = 0 \\ (x + 3) (x - 2) = 0 \\ x = - 3 x = 2 \end{aligned}

$\begin{align*}x^2+x>6\\ \underline{\ \ \ -6 \ -6} \\ x^2+x-6>0 \\ \\ x^2+x-6=0 \\ (x+3)(x-2)=0 \\ x=\text{-}3 \ \ x=2\end{align*}$
::x2+x>6 - 6 - 6 - 6_ x2+x - 6 - 0x2+x6=0(x+3)(x-2)=0x=3 x=2

Now that we know the values of the x -intercepts, we can consider a sketch of the graph. The leading coefficient , $\begin{align*}a\end{align*}$ , is positive. Therefore, the parabola opens upward and it goes through (-3,0) and (2,0). We can draw a sketch of the graph with this information.
::现在我们知道 X 界面的值, 我们可以考虑图形的草图。领先系数是正数。因此, 抛物线向上打开, 穿过( 3,0) 和 (2,0) 。我们可以用这个信息绘制图表的草图。

lesson content

Reading the graph, we notice the following properties:
::读取图表时,我们注意到以下属性:

If $\begin{align*}\text{-}3 < x < 2\end{align*}$ , then $\begin{align*}f(x)>0\end{align*}$ .
::如果 -3 <x<2,则f(x)>0。

If $\begin{align*}\text{-}3 < x < 2\end{align*}$ , then $\begin{align*}f(x)<0\end{align*}$ .
::如果 -3 <x<2,则f(x) <0。

If $\begin{align*}x>2\end{align*}$ , then $\begin{align*}f(x)>0\end{align*}$ .
::如果 x> 2, 那么 f( x) > 0 。

Therefore, $\begin{align*}x^{2}+x-6>0\end{align*}$ whenever $\begin{align*}x<\text{-}3\end{align*}$ or $\begin{align*}x>2\end{align*}$ , or $\begin{align*}(\text{-}\infty,\text{-}3) \cup (2,\infty)\end{align*}$ .
::因此,在 x2+x-6>0 x < 3 或 x>2 或 (- , 3) 或 (2, ) 的情况下, x2+x-6>0 。

Example 2
::例2

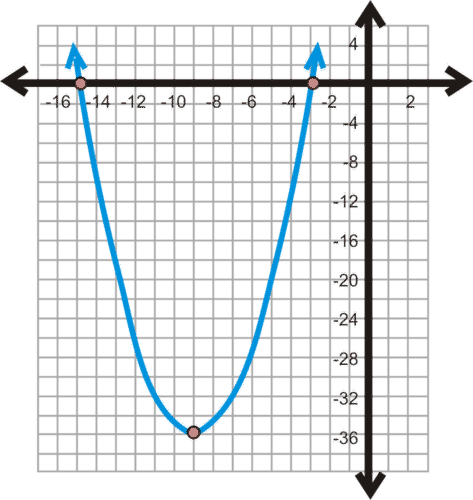
Solve $\begin{align*}x^2+18x+45 \le 0\end{align*}$ graphically.
::以图形方式解决 x2+18x+45_0 。

Solution: Since this example already has all the terms on one side of the inequality, we can skip that step. Our 1st step will be to set the left side of the inequality equal to 0, and solve for x . This will provide us with the x- intercepts for the graph of our quadratic inequality.
::解决方案: 既然这个例子已经具备了不平等的一面的所有条件, 我们可以跳过这一步。我们的第一个步骤是将不平等的左侧设为 0, 并解决 x。这将为我们提供我们二次不平等图的 X 解答。

\begin{aligned} x^{2} + 18 x + 45 = 0 \\ (x + 15) (x + 3) = 0 \\ x + 15 = 0 x + 3 = 0 \\ x = - 15 x = - 3 \end{aligned}

$\begin{align*}x^2+18x+45=0 \\ (x+15)(x+3) = 0 \\ x+15=0 \ \ x+3=0 \\ x=\text{-}15 \ \ \ x=\text{-}3\end{align*}$
::x2+18x+45=0(x+15)(x+3)=0x+15=0xx=0x3=0x=0x=0x=0x=15x=3

So the x- intercepts are (-15, 0) and (-3, 0). Since $\begin{align*}a=1>0\end{align*}$ , the parabola opens upward.
::所以 x 界面是 (-15, 0) 和 (-3, 0) 。由于 a= 1 > 0, 抛物线向上打开。

Here is the graph:
::以下是图表:

lesson content

As we can see from the graph, $\begin{align*}f(x) \le 0\end{align*}$ when $\begin{align*}x\end{align*}$ is between -15 and -3. The solution is $\begin{align*}\text{-}15 \le x \le \text{-}3\end{align*}$ or $\begin{align*}[\text{-}15, \text{-}3]\end{align*}$ .
::从图表中可以看出,当x在 -15 和 -3之间时 f(x)_0。溶液为 -15x%-3 或 [15-3 。

by Mathcasts demonstrates how to solve quadratic inequalities graphically.
::以图形方式展示如何解决二次不平等。

How To Solve a Quadratic Inequality With a Graphing Utility
::如何解决与图图用途的赤道不平等

Graph each side of the inequality on the same set of axes and analyze the graph. See the example below.

Example 3
::例3

A player's OPS throughout his career can be modeled by the function
::玩家的整个职业生涯的OPS 可以通过这个功能来模拟

\begin{aligned} f (x) = - 0.53 x^{2} + 4.39 x + 824.03. \end{aligned}

$\begin{align*}f(x)=-0.53x^2+4.39x+824.03.\end{align*}$
::f(x) =================================================================================================================== =====================================================================================================================================================================================================================================================================================================================================================================================================

where x is years after age 25 ( $\begin{align*}x=0\end{align*}$ corresponds to being 25 years old) and $\begin{align*}f(x)\end{align*}$ is the player's OPS (times 1,000 to remove the decimal). When will the player have an OPS above 750?
::25岁之后的 x 年(x=0 表示为25岁), F(x) 是玩家的 OPS (乘以 1 000 来删除小数) 。玩家的 OPS 什么时候能超过 750 ?

Solution: We can graph $\begin{align*}f(x)\end{align*}$ and $\begin{align*}y=750\end{align*}$ on the same set of axes and then analyze our graph.
::解答: 我们可以在同一组轴上绘制f(x)和y=750图, 然后分析我们的图表。

The parabola is above the line between 0 and 16.583 years, so the player will have an OPS above 750 when his age is $\begin{align*}25 \le x <41.583\end{align*}$ or $\begin{align*}[25,41.583)\end{align*}$ .
::抛物线高于0至16.583年的线条,因此,当玩家的年龄为25x<41.583或[25,41.583]时,其OPS值将高于750。

Example 4
::例4

Solve $\begin{align*}x^{2}+2x-8>0\end{align*}$ algebraically.
::溶解 x2+2x-8>0 代数。

Solution: First, solve the quadratic equation.
::解答:首先,解答二次方程。

\begin{aligned} x^{2} + 2 x - 8 = 0 \\ (x + 4) (x - 2) = 0 \\ x + 4 = 0 x - 2 = 0 \\ x = - 4 x = 2 \end{aligned}

$\begin{align*}x^2 + 2x - 8 = 0\\ (x+4)(x-2)=0 \\ x+4=0 \ \ x-2=0 \\ x=\text{-}4 \ \ \ x=2\end{align*}$
::x2+2x_8=0(x+4)(x-2)=0x+4=0x=0x2=0x=0x=0x=4x=4x=2

T he two solutions to this quadratic equation are $\begin{align*}x = \text{-}4\end{align*}$ and $\begin{align*}x = 2\end{align*}$ , thus, the $\begin{align*}x-\end{align*}$ intercepts of the function $\begin{align*}f(x) = x^{2} + 2x - 8\end{align*}$ are (-4,0) and (2,0).
::此二次方程式的两个解决方案是 x=4 和 x=2, 因此函数 f( x) =x2+2x-8的 x- interfits( 4, 0) 和 2,0 。

These points divide the x- axis into three intervals: $\begin{align*}(\text{-}\infty,\text{-}4), (\text{-}4,2), \;\text{and}\; (2,\infty)\end{align*}$ . We can choose a test point from each interval, substitute it into $\begin{align*}f(x)\end{align*}$ and see if the function is negative or positive with that value as x . This procedure can be simplified by making a table as shown below:
::这些点将 x 轴分为三个间隔- , 4, 4, 2, 和 (2, 2, 2) 。我们可以从每个间隔选择一个测试点, 将其替换为 f( x) , 并查看该函数是否为负值或正值, 如 x。这个程序可以通过以下表格简化 :

Interval	Test Point	*Is $\begin{align}x^{2}+2x-8\end{align}$ positive or negative?*	Part of Solution set?
$\begin{align}(\text{-}\infty,\text{-}4)\end{align}$	$\begin{align}\text{-}5\end{align}$	$\begin{align}(\text{-}5)^2+2(\text{-}5)-8=25-10-8=7 \qquad \text{positive}\end{align}$	$\begin{align}yes\end{align}$
$\begin{align}(\text{-}4, 2)\end{align}$	$\begin{align}1\end{align}$	$\begin{align}(1)^2+2(1)-8=1+2-8=\text{-}5 \qquad \text{negative}\end{align}$	$\begin{align}no\end{align}$
$\begin{align}(2,+\infty)\end{align}$	$\begin{align}3\end{align}$	$\begin{align}3^2+2(3)-8=9+6-8=7 \qquad \text{positive}\end{align}$	$\begin{align}yes\end{align}$

From the table, we conclude that since $\begin{align*}x^2 +2x -8 > 0\end{align*}$ if $\begin{align*}x < \text{-}4\end{align*}$ and $\begin{align*}x > 2\end{align*}$ . The solution set can also be written as
::从表中,我们得出的结论是,自 x2+2x-8>0 以来,如果 x < 4和 x>2, 则设定的解决方案也可以以下列方式书写:

\begin{aligned} x \in (- \infty, - 4) \cup (2, + \infty) . \end{aligned}

$\begin{align*}x\in(\text{-}\infty,\text{-}4)\cup(2,+\infty).\end{align*}$
::

Example 5
::例5

Find the solution set of the inequality $\begin{align*}x^2 \leq 16\end{align*}$ .
::寻找不平等的解决方案集 x216 。

Solution: Arrange the inequality so all the terms are one one side, and then set the function equal to 0.
::解决方案:安排不平等性,使所有条件都以一面为一面,然后将功能设为0。

\begin{aligned} x^{2} \leq 16 \\ x^{2} - 16 \leq 0 \\ x^{2} - 16 = 0 \\ (x + 4) (x - 4) = 0 \\ x + 4 = 0 x - 4 = 0 \\ x = - 4 x = 4 \end{aligned}

$\begin{align*}x^2 \le 16 \\ x^2-16 \le 0\\ \\ x^2 - 16 = 0 \\ (x+4)(x-4)=0 \\ x+4=0 \ \ \ x-4=0 \\ x=\text{-}4 \ \ \ x=4 \\\end{align*}$
::x2_16x2 - 16_0x2 - 16=0(x+4)(x- 4)=0x+4=0x4=0 x4=0 x4=0x=0x=4x=4

That gives us three intervals on the graph:
::这让我们在图表上间隔了三个间隔:

\begin{aligned} x \leq - 4 \end{aligned}

$\begin{align*}x \leq \text{-}4\end{align*}$
::x-4

\begin{aligned} - 4 \leq x \leq 4 \end{aligned}

$\begin{align*}\text{-}4 \leq x \leq 4\end{align*}$
::- 4x4 - 4x4 - 4x4 - 4x4 - 4x4

$\begin{align*}4 \leq x\end{align*}$
::4x

Test one value from each interval to identify possible solution sets.
::每个间隔测试一个值,以确定可能的解决方案集。

Set	$\begin{align}x \leq \text{-}4\end{align}$	$\begin{align}\text{-}4 \leq x \leq 4\end{align}$	$\begin{align}4 \leq x\end{align}$
Test value	$\begin{align}\text{-}5\end{align}$	0	$\begin{align}5\end{align}$
$\begin{align}f(x)\end{align}$ true with value?	$\begin{align}4\cdot(\text{-}5)^2 = 100 \nleq 16\end{align}$ $\begin{align}\therefore No\end{align}$	$\begin{align}4\cdot 0^2 = 0 \leq 16\end{align}$ $\begin{align}\therefore Yes\end{align}$	$\begin{align}4\cdot5^2 = 100 \nleq 16\end{align}$ $\begin{align}\therefore No\end{align}$

Therefore, the solution set is $\begin{align*}\text{-}4 \leq x \leq 4\end{align*}$ or $\begin{align*}[\text{-}4,4]\end{align*}$ .
::因此,所设定的解决方案是4x4或[4-4]。

by Mathispower4u demonstrates how to solve quadratic inequalities algebraically .
::Mathispower4u 演示如何从代数角度解决二次不平等。

Example 6
::例6

Solve the following inequalities: $\begin{align*}\text{-}x^2 \ge 0, \ \text{-}x^2 > 0, \ \text{-}x^2<0, \ \text{-}x^2 \le 0.\end{align*}$
::解决以下不平等: -x20, -x2>0, -x2<0, -x20。

Solution: Let's consider the graph of $\begin{align*}y=\text{-}x^2\end{align*}$ .
::解答:让我们考虑一下y=-x2的图表。

$\begin{align*}\text{-}x^2 \ge 0\end{align*}$ : The graph is never above the x- axis. The only solution is $\begin{align*}x=0\end{align*}$ .
::-x20: 图形从不高于 x 轴。唯一的溶液是 x=0 。

$\begin{align*}\text{-}x^2>0\end{align*}$ : Because of the previous reasoning, there are no solutions.
::-x2>0:由于先前的推理,没有解决办法。

$\begin{align*}\text{-}x^2<0\end{align*}$ : This is true for all real numbers except 0, so $\begin{align*}(\text{-}\infty,0) \cup (0,\infty).\end{align*}$
::-x2<0:除 0 外,所有真实数字都是如此, 所以 (- , 0) (0, ) 。

$\begin{align*}\text{-}x^2 \le 0\end{align*}$ : This is true for all real numbers, so $\begin{align*}(\text{-}\infty, \infty).\end{align*}$
::-x20:所有真实数字都是如此,所以(-,)。

Summary
::摘要

To solve a quadratic inequality, arrange the terms on one side of the inequality, so that the other side is equal to 0. Then solve the quadratic equation associated with the function. This will give you the x- intercepts. Then choose from:
- Graphical approach: Sketch a graph of the quadratic function using the x- intercepts and whether the parabola opens upward or downward. Read the graph.
  ::图形化方法:用 X 界面以及抛物线向上还是向下打开来绘制二次函数的图形。读取图形。
- Algebraic approach: Pick test points in each interval created by the x- intercepts. Determine if the test points satisfy the inequality.
  ::代数法:在 x intercuts 创造的每个间隔中选择测试点。确定测试点是否满足了不平等。
::要解决二次不平等, 请在二次不平等的一方排列条件, 使另一方等于 0 。然后解答与函数相关的二次方程。这将为您提供 x 界面。然后从 : 图形化 : 使用 x 界面和 parbola 向上还是向下打开来绘制一个二次函数图。读下图。代数法 : 在 x 界面创建的每个间隔中选择测试点。确定测试点是否满足不平等。

Review
::回顾

Solve.
::解决。

1. $\begin{align*}x^2 + 9x > -14\end{align*}$
::1. x2+9x14

2. $\begin{align*}x^2 -5x \leq 50\end{align*}$
::2. x2 - 5x=50

3. $\begin{align*}x^2 + 2x \leq 48\end{align*}$
::3. x2+2x48

4. $\begin{align*}x^2 -20 - 8x < 0\end{align*}$
::4. x2-20-8x < 0

5. $\begin{align*}x^2 + 10x \geq \text{-}21\end{align*}$
::5. x2+10xXX-21

6. $\begin{align*}(x + 6)(x - 3) > 0\end{align*}$
::6. (x+6)(x-3)>0

7. $\begin{align*}(x - 8)(x + 1) > 0\end{align*}$
::7. (x-8)(x+1)>0

8. $\begin{align*}x^2 - x \geq 90\end{align*}$
::8. x2-x%90

9. $\begin{align*}3x^2 - 23x \leq 8\end{align*}$
::9. 3x2-23x8

10. $\begin{align*}x^2 + x - 6 > 0\end{align*}$
::10. x2+x-6>0

Explore More
::探索更多

1. Suppose John throws his keys out of his car, which is 10 feet above the ground, hoping his friend Tom will catch them. The keys follow the projectile $\begin{align*}h(t) = \text{-}16t ^2 + 6\end{align*}$ . Also, suppose Tom is only able to catch the keys when they are between 2 feet and 5 feet above the ground. Between what times can Tom catch the keys?
::1. 假设约翰把钥匙扔出车外,车距地面10英尺,希望他的朋友汤姆能抓住钥匙,钥匙跟着弹壳H(t)=16t2+6,假设汤姆只能在地上2英尺到5英尺之间才能抓住钥匙。在什么时候汤姆能抓住钥匙?

2. A stuntman is going to jump off a building that is 20 meters high. Suppose a video camera is set up to film him when he is between 15 m and 10 m above the ground. How long after the stuntman jumps should the camera film him?
::2. 特技人员将跳下一座20米高的大楼,如果在地面上15米至10米之间设置摄像头拍摄他的话,特技人员将跳下一座20米高的大楼。

3. Jen is building a new house. She wants her house to be larger than her neighbor's house, which is 1,200 ft ² . However, she wants her house to be smaller than her sister's house, which is 4,000 ft ² . Moreover, she wants her house to be a raised ranch (the living area will be a rectangular prism) with two floors. Finally, she would like the length to be 10 ft longer than the width to account for the garage. What range of dimensions could Jen use for her house?
::3. Jen正在建造一座新房子,她希望她的房子比邻居的房子大1 200英尺,然而,她希望她的房子比姐姐的房子小4 000英尺,另外,她希望她的房子是一个有两层楼的养大牧场(居住区将是长方形棱柱),最后,她希望车库的长度比宽度长10英尺。

4. A rain boot company has determined that the revenue from the sale of x rain boots can be modeled with the equation $\begin{align*}R(x) = \text{-}x^2 + 15x\end{align*}$ . In this equation, $\begin{align*}R(x)\end{align*}$ represents the revenue. Moreover, the company has determined that the cost of making x rain boots can be modeled by the equation $\begin{align*}C(x) = 135-17x\end{align*}$ . In this equation, $\begin{align*}C(x)\end{align*}$ represents the cost. For what value(s) of x will the company break even or make a profit?
::4. 一家雨靴公司确定,出售X雨靴的收入可以以R(x)=-x2+15x等式模拟。在这个等式中,R(x)代表收入;此外,该公司确定,制作x雨靴的费用可以以C(x)=135-17x等式模拟。在这个等式中,C(x)代表成本。对于x的价值,公司会折损还是赢利?

5. A smart fitness wristband company has determined that the cost ( $\begin{align*}C(x)\end{align*}$ ) and revenue ( $\begin{align*}R(x)\end{align*}$ ) of making x wristbands can be modeled by the following equations: $\begin{align*}C(x) = 253-7x, \ R(x) = 27x-x^2\end{align*}$ . For what value(s) of x will the company break even or make a profit?
::5. 一家智能健身手腕带公司确定,制作X手腕带的成本(C(x))和收入(R(x))可以用下列方程式建模:C(x)=253-7x、R(x)=27x-x2. 公司平价或盈利的x值是多少?

6. You are supposed to mow your square-shaped lawn for your parents, but the mower has only part of a tank of gas. If you can mow 2,500 sf per gallon, and the mower has approximately 2.5 gallons in it, what is the maximum length of one side of the lawn you can mow? If your lawn is 75 feet long, will you need more gas?
::6. 你本该为父母修剪草坪,但割草机只有油箱的一部分,如果每加仑可修剪2,500索夫,而除草机内约有2.5加仑,那么你可修剪的草坪一侧最长长度是多少?如果草坪长75英尺,你还需要更多的油吗?

7. A rectangle has a length 10 meters more than twice the width. Find all of the possible widths that result in the area of the rectangle not exceeding 100 squared meters.
::7. 矩形的长度为宽度的10米以上,是宽度的两倍,查找所有可能导致矩形区域不超过100平方米的宽度。

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

References
::参考参考资料

1. Fair, Ray C. "Estimated Age Effects in Baseball." Journal of Quantitative Analysis in Sports 4, no. 1 (2008). doi:10.2202/1559-0410.1074.
::1. 公平,Ray C. "棒球估计年龄影响",《体育定量分析杂志》,第4期,第1期(2008年)。 doi:10.2202/1559-0410.1074。

Interval	Test Point	*Is $\begin{align}x^{2}+2x-8\end{align}$ positive or negative?*	Part of Solution set?
$\begin{align}(\text{-}\infty,\text{-}4)\end{align}$	$\begin{align}\text{-}5\end{align}$	$\begin{align}(\text{-}5)^2+2(\text{-}5)-8=25-10-8=7 \qquad \text{positive}\end{align}$	$\begin{align}yes\end{align}$
$\begin{align}(\text{-}4, 2)\end{align}$	$\begin{align}1\end{align}$	$\begin{align}(1)^2+2(1)-8=1+2-8=\text{-}5 \qquad \text{negative}\end{align}$	$\begin{align}no\end{align}$
$\begin{align}(2,+\infty)\end{align}$	$\begin{align}3\end{align}$	$\begin{align}3^2+2(3)-8=9+6-8=7 \qquad \text{positive}\end{align}$	$\begin{align}yes\end{align}$

Set	$\begin{align}x \leq \text{-}4\end{align}$	$\begin{align}\text{-}4 \leq x \leq 4\end{align}$	$\begin{align}4 \leq x\end{align}$
Test value	$\begin{align}\text{-}5\end{align}$	0	$\begin{align}5\end{align}$
$\begin{align}f(x)\end{align}$ true with value?	$\begin{align}4\cdot(\text{-}5)^2 = 100 \nleq 16\end{align}$ $\begin{align}\therefore No\end{align}$	$\begin{align}4\cdot 0^2 = 0 \leq 16\end{align}$ $\begin{align}\therefore Yes\end{align}$	$\begin{align}4\cdot5^2 = 100 \nleq 16\end{align}$ $\begin{align}\therefore No\end{align}$

章节大纲

Quadratic Inequalities ::赤道不平等

How To Solve a Quadratic Inequality ::如何解决赤道不平等问题

Example 1 ::例1

Example 2 ::例2

How To Solve a Quadratic Inequality With a Graphing Utility ::如何解决与图图用途的赤道不平等

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

References ::参考参考资料

Quadratic Inequalities
::赤道不平等

How To Solve a Quadratic Inequality
::如何解决赤道不平等问题

Example 1
::例1

Example 2
::例2

How To Solve a Quadratic Inequality With a Graphing Utility
::如何解决与图图用途的赤道不平等

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

References
::参考参考资料