节: 线线和二次赤道系统 | 12.8 线性线性电弧和二次电解系统

章节大纲

A camera business has fixed costs of $4,000, and it costs $100 to produce each camera. The price-demand equation, the price given a number of cameras consumers want to buy, can be modeled by $\begin{align*}p=500-0.125q,\end{align*}$ where $\begin{align*}p\end{align*}$ is the price and $\begin{align*}q\end{align*}$ is the quantity demanded. How many cameras need to be sold to reach what is called the "break-even point," the point at which the costs equal the revenue generated from selling a product?
::摄影机企业固定成本为4000美元,每台摄影机生产成本为100美元。价格需求方程式 — — 给一些消费者想要购买的照相机的价格 — — 可以通过p=500-0.125q(p=500-0.125q)模拟,p是价格,q是所需数量。需要出售多少相机才能达到所谓的“平衡点 ” , 即成本等于销售产品所得收入的点?

For this example, the revenue model will be a quadratic function, and the cost model will be a linear function. How can we determine when they are equal? In this section, we discuss how to solve a system of equations involving .
::例如,收入模式将是一个二次函数,而成本模式将是一个线性函数。我们如何确定它们何时相等?在本节中,我们讨论如何解决一个包含等式的体系。

Solving Systems of Conic Sections
::二次元件的溶解系统

In the chapter on solving systems of linear equations, we solved a system involving two lines or three planes by using graphing, substitution, and elimination by addition . Here we will consider systems of equations that include conic sections, and, once again, we will see that we can use any of these techniques to solve a system of equations.
::在解决线性方程式体系的章节中,我们通过使用图形化、替代和加法去除,解决了涉及两线或三平面的体系。在这里,我们将考虑包含二次方程式部分的方程式体系,我们将再次看到,我们可以使用其中任何一种方法来解决方程式体系。

Unlike our previous systems of equations, we will see that with conic sections there will often be more than one solution . Previously, we defined a solution to a system of equations as a point that satisfied all equations in the system. Graphically, these are points on both graphs or points where the two graphs intersect.
::与我们以往的方程式体系不同,我们可以看到,有二次曲线段的解算方法往往不止一个。以前,我们定义了方程式体系的解析方法,作为满足系统中所有方程式的点。从图形上看,这些是两个图形或两个图形交叉点上的点。

Example 1
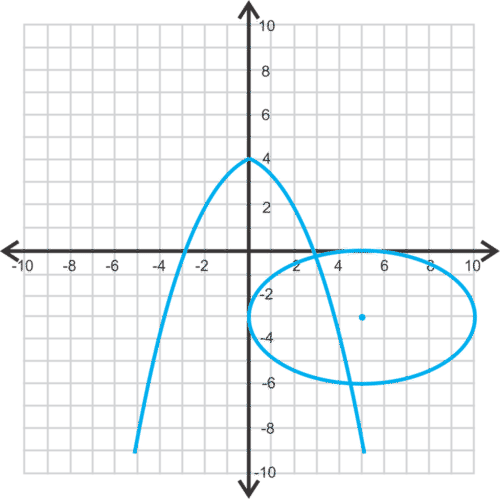
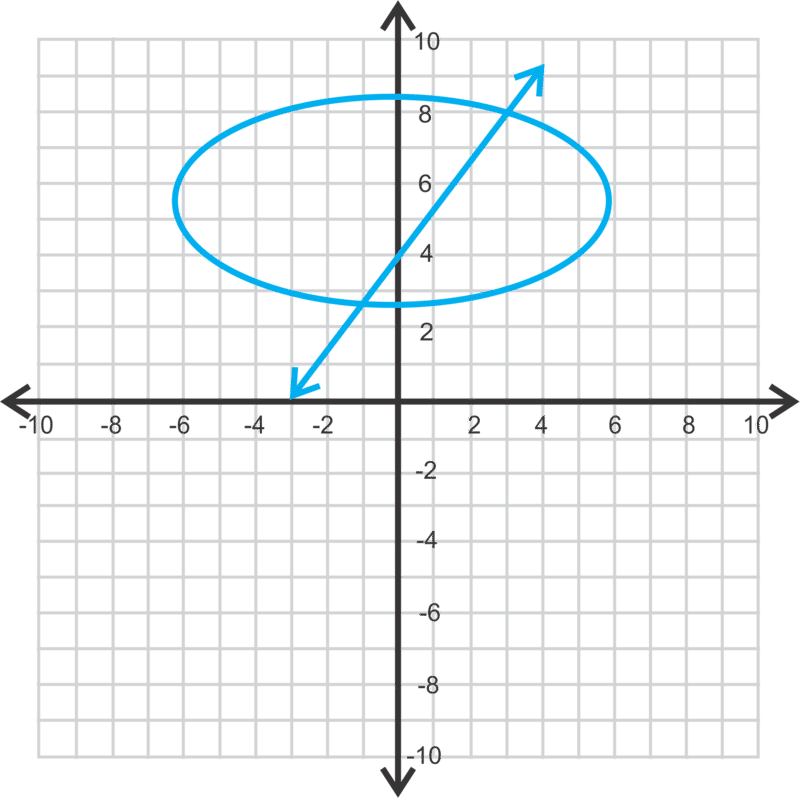
::例1

Estimate the solutions to the system below.
::下文对系统的解决办法作出估计。

Solution: It appears that these two graphs intersect at approximately $\begin{align*}(3, \text{-}0.1)\end{align*}$ and $\begin{align*}(4.5, \text{-}6)\end{align*}$ .
::解决办法:看来这两个图表大约在(3,0.1)和(4.5,-6)之间交叉。

Example 2
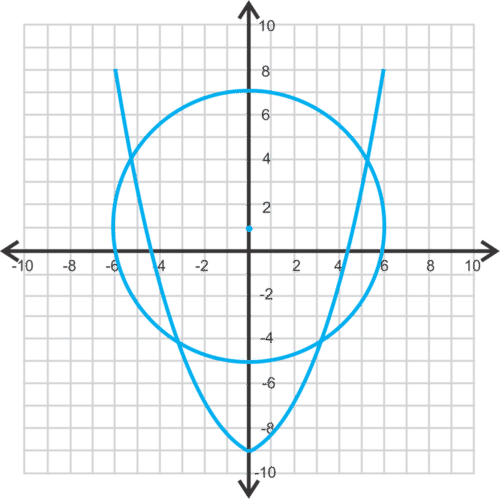
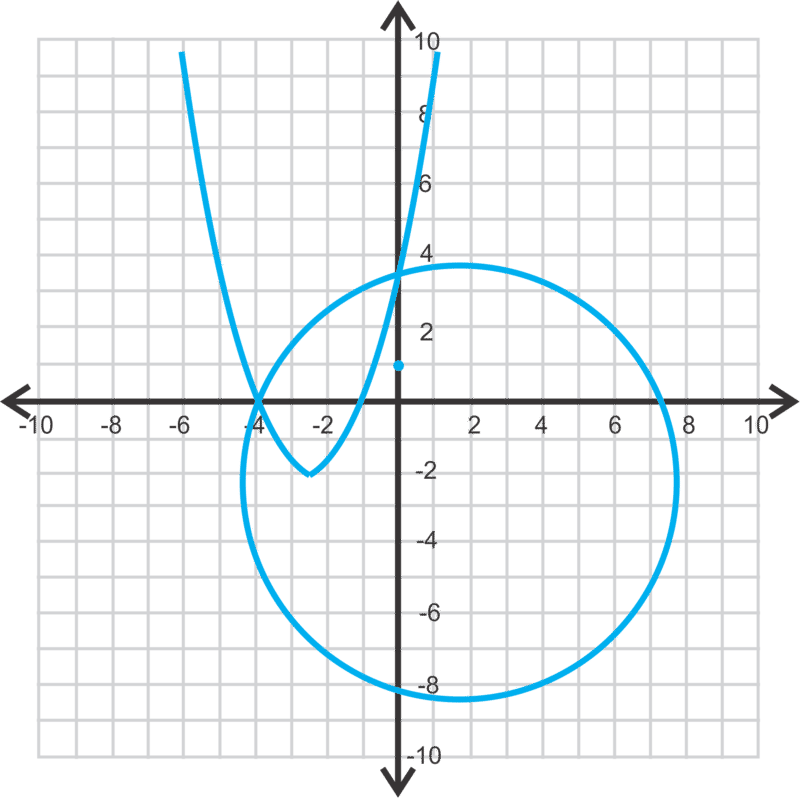
::例2

Estimate the solutions for the system of equations below.
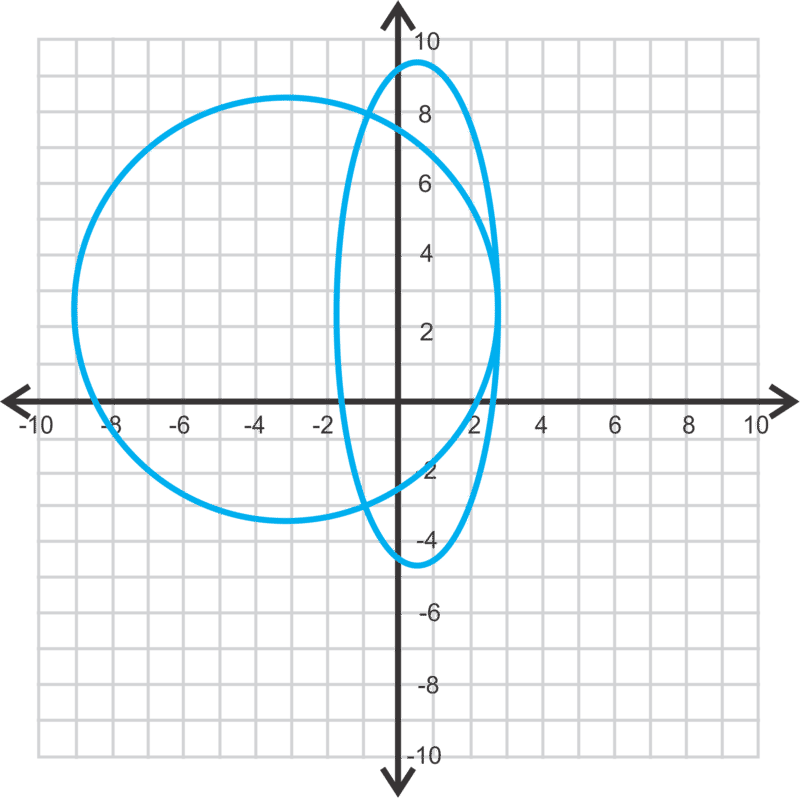
::估计以下方程式系统的解决办法。

Solution: These two intersect in four places. The intersections look to be approximately at the following points:
::溶液:这两个交叉点在四个地方交叉。十字路口大致位于以下各点:

$\begin{align*}(0, 7)\end{align*}$ , $\begin{align*}(4.7, 5.5)\end{align*}$ , $\begin{align*}(4.9, 4.3)\end{align*}$ , and $\begin{align*}(\text{-}1, 2.9)\end{align*}$
:0,7,(4,7,7,7.5.5,(4.9,4.3))和(-1,2.9)

Keep in mind these are only estimates. In the examples below, we will show how to find the exact solutions using the techniques we discussed in the chapter on solving systems of equations.
::铭记这些只是估计数字,在下面的例子中,我们将说明如何利用我们在解决方程式体系一章中讨论的技术找到确切的解决办法。

Example 3
::例3

Solve
$\begin{aligned} x^{2} + y^{2} & = 25 \\ 3 x + 2 y & = 6. \end{aligned}$
$\begin{align*}x^2+y^2 &=25 \\ 3x+2y &=6.\end{align*}$
::溶解 x2+y2=253x+2y=6。

Solution: Since there are no like terms that we could eliminate if we did elimination by addition, we need to use substitution. Let's solve for $\begin{align*}y\end{align*}$ in the linear equation, and then substitute that into the equation of the circle .
::解答:既然我们用加法来消除的话, 我们无法消除这样的术语, 我们需要使用替代。让我们用线性方程来解决y, 然后将它替换为圆形的方程。

$\begin{aligned} 3 x + 2 y = 6 \\ 2 y = - 3 x + 6 \\ y = - \frac{3}{2} x + 3 \\ x^{2} + {(- \frac{3}{2} x + 3)}^{2} & = 25 \\ x^{2} + \frac{9}{4} x^{2} - 9 x + 9 & = 25 \\ \frac{13}{4} x^{2} - 9 x - 16 & = 0 \\ 13 x^{2} - 36 x - 64 & = 0 \end{aligned}$
$\begin{align*}3x+2y=6 \\ 2y=\text{-}3x+6 \\ y=\text{-}\frac{3}{2}x+3 \\ \\ x^2+\left(\text{-}\frac{3}{2}x+3\right)^2 &=25 \\ x^2+\frac{9}{4}x^2-9x+9 &=25 \\ \frac{13}{4}x^2-9x-16 &=0 \\ 13x^2-36x-64 &=0\end{align*}$
::3x+2y=62y=3x6y=3x6y=-32x+3x2+(- 32x+3)2=25x2+94x2-9x+9=25134x2-9x9=25134x2-9x16=013x2-36x-64=0

Use the quadratic formula:
::使用二次公式 :

$\begin{aligned} x & = \frac{36 \pm \sqrt{36^{2} - 4 (13) (- 64)}}{2 (13)} \\ = \frac{36 \pm \sqrt{4624}}{26} \\ = \frac{36 \pm 68}{26} \end{aligned}$
$\begin{align*}x &= \frac{36 \pm \sqrt{36^2-4(13)(\text{-}64)}}{2(13)} \\ &= \frac{36 \pm \sqrt{4624}}{26} \\ &= \frac{36 \pm 68}{26}\end{align*}$
::x=36362-4(13) (-642(13) =36462426=366826)

The solutions for $\begin{align*}x\end{align*}$ are $\begin{align*}\frac{36+68}{26}=4\end{align*}$ and $\begin{align*}\frac{36-68}{26}=\text{-}1\frac{3}{13}\end{align*}$ . Plug these into either equation to solve for $\begin{align*}y,\end{align*}$ although it is probably easier to use the linear equation.
::x 的解决方案是 36+6826=4和 36-6826=-133. 将这些插入y 的任何一个方程中,尽管使用线性方程可能比较容易。

$\begin{aligned} y & = - \frac{3}{2} (4) + 3 = - 3 \\ y & = - \frac{3}{2} (- \frac{16}{13}) + 3 = 4 \frac{11}{13} \end{aligned}$
$\begin{align*}y&=\text{-}\frac{3}{2}(4)+3=\text{-}3 \\ \\ y&=\text{-}\frac{3}{2} \left(\text{-}\frac{16}{13}\right)+3=4 \frac{11}{13}\end{align*}$
::y=-32(4)+3=-3y=-32(-1613)+3=41113

The points are $\begin{align*}(4, \text{-}3)\end{align*}$ and $\begin{align*}\left(\text{-}1 \frac{3}{13}, 4 \frac{11}{13}\right)\end{align*}$ .
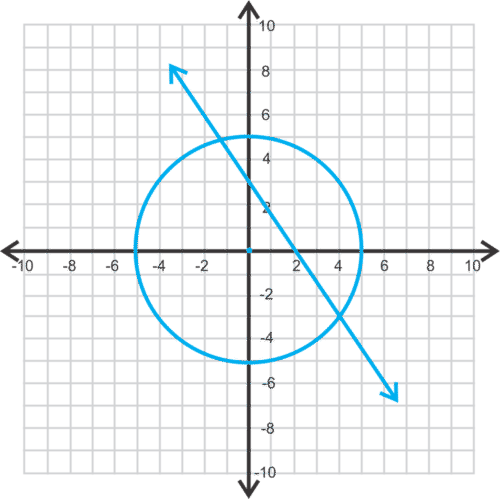
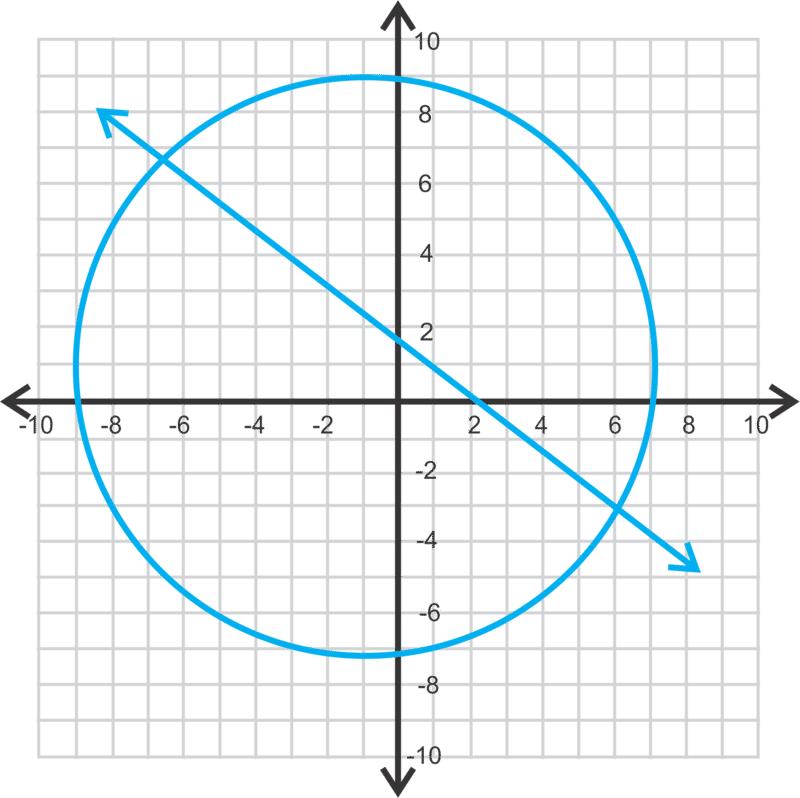
::要点是(4,3)和(1313,34,1113)。

We can also estimate the solutions to this system by graphing. The 1st equation is a circle, centered at the origin, with a radius of 5. The 2nd equation is a line.
::我们也可以通过图形化来估计这个系统的解决方案。第一个方程式是一个圆形, 以原点为中心, 半径为 5 。第二个方程式是一条线。

Now let's estimate where the line and circle intersect. In the 2nd quadrant, it looks like $\begin{align*}(\text{-}1.2, 4.8),\end{align*}$ and in the 4th quadrant, it looks like $\begin{align*}(4, \text{-}3)\end{align*}$ . These are our estimated solutions. Notice they are close in value to our actual solutions.
::现在让我们来估计一下线和圆的交叉点。在第二个象体中, 它看起来像( 1.2, 4. 8) , 在第四个象体中, 它看起来像( 4, 3) 。这些是我们估计的解决方案。注意它们与我们的实际解决方案非常接近。

by CK-12 shows how to solve a system of equations with a conic section by substitution.
::的 CK-12 显示如何通过替换解决带有二次曲线部分的方程系统。

Example 4
::例4

Solve
$\begin{aligned} \frac{x^{2}}{16} + \frac{y^{2}}{9} = 1 \\ y^{2} = - \frac{4}{3} (x - 6) . \end{aligned}$
$\begin{align*}& \frac{x^2}{16} + \frac{y^2}{9}=1 \\ & y^2=\text{-}\frac{4}{3}(x-6).\end{align*}$
::溶解 x216+y29=1y2=-43(x-6)

Solution: Since $\begin{align*}y^2\end{align*}$ is isolated in the 2nd equation and it appears in the 1st equation, we can use substitution to solve.
::解答:由于 y2 在第二个方程式中被孤立并且它出现在第一个方程式中, 我们可以使用替换来解答。

$\begin{aligned} \frac{x^{2}}{16} - \frac{4 (x - 6)}{3 \cdot 9} & = 1 \\ \frac{x^{2}}{16} - \frac{4 x - 24}{27} & = 1 \\ 27 x^{2} - 16 (4 x - 24) & = 432 \\ 27 x^{2} - 64 x - 48 & = 0 \end{aligned}$
$\begin{align*}\frac{x^2}{16} - \frac{4(x-6)}{3 \cdot 9} &= 1 \\ \frac{x^2}{16} - \frac{4x-24}{27} &=1 \\ 27x^2-16(4x-24) &=432 \\ 27x^2-64x-48 &=0\end{align*}$
::x216-4(x-6)39=1x216-4x-2427=127x2-16(4x-24)=43227x2-64x-48=0

Now use the quadratic formula to solve for $\begin{align*}x\end{align*}$ .
::现在使用二次方程式解析 x。

$\begin{aligned} x & = \frac{64 \pm \sqrt{(- 64)^{2} - 4 (27) (- 48)}}{2 (27)} \\ = \frac{64 \pm \sqrt{9, 280}}{54} \\ = \frac{32 \pm 4 \sqrt{145}}{27} \end{aligned}$
$\begin{align*}x &= \frac{64 \pm \sqrt{(\text{-}64)^2-4(27)(\text{-}48)}}{2(27)} \\ &= \frac{64 \pm \sqrt{9,\!280}}{54} \\ &= \frac{32 \pm 4 \sqrt{145}}{27}\end{align*}$
::x=64(-64)2-4(27)(-482(27)=649,28054=32414527)

Plugging these into the calculator, we get $\begin{align*}x = \frac{32+4 \sqrt{145}}{27} \approx 2.97\end{align*}$ and $\begin{align*}x = \frac{32-4 \sqrt{145}}{27} \approx \text{-}0.6\end{align*}$ .
::把这些插进计算器,我们得到x=32+4145272.97和x=32-414527-0.6。

Next we solve for $\begin{align*}y\end{align*}$ . We can choose either equation.
::接下来我们为y解决。我们可以选择两个方程中的任何一个。

$\begin{aligned} y^{2} & = - \frac{4}{3} (2.97 - 6) y^{2} = - \frac{4}{3} (- 0.6 - 6) \\ y^{2} & = 4.04 and y^{2} = 8.8 \\ y & = \pm 2.01 y = \pm 2.97 \end{aligned}$
$\begin{align*}y^2 &= \text{-}\frac{4}{3}(2.97-6) \qquad \qquad \quad \quad y^2= \text{-}\frac{4}{3}(\text{-}0.6-6) \\ y^2 &= 4.04 \qquad \qquad \qquad \text{and} \qquad \ y^2= 8.8 \\ y &= \pm 2.01 \qquad \qquad \qquad \qquad \quad \ \ y= \pm 2.97\end{align*}$
::y2=-43(2.97-6)y2=-43(-0.6-6)y2=4.04和y2=8.8y@2.01y2.97

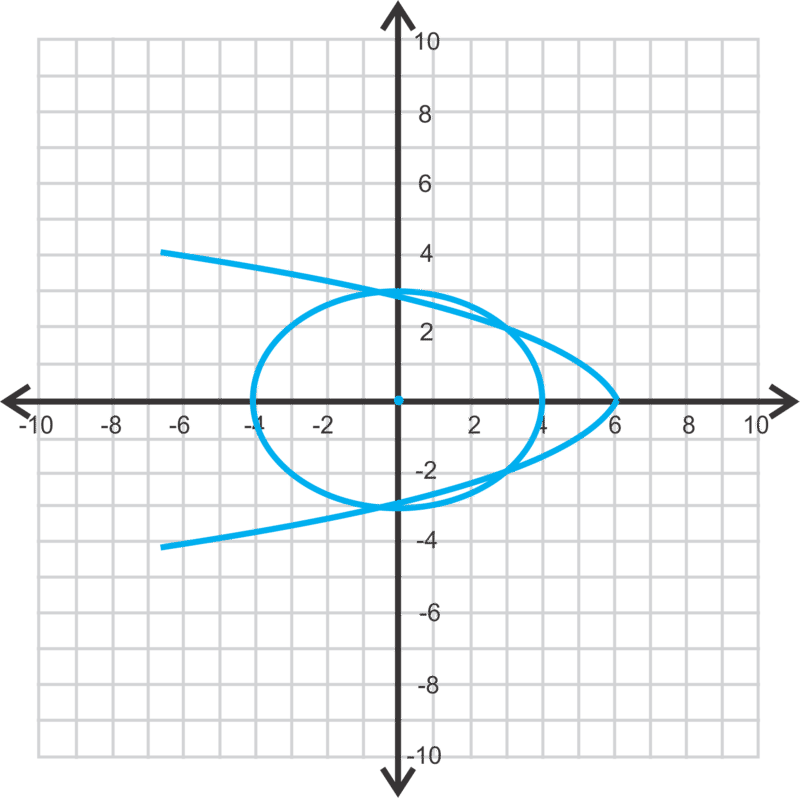
The points are $\begin{align*}(2.97, 2.01)\end{align*}$ , $\begin{align*}(2.97, \text{-}2.01)\end{align*}$ , $\begin{align*}(\text{-}0.6, 2.97)\end{align*}$ , and $\begin{align*}(\text{-}0.6, \text{-}2.97)\end{align*}$ .
::要点是(2.972.01)、2.972.01、2.972.01、(-0.6 2.97)和(-0.6、2.97)。

Looking at the graph, we can see these four points of intersection or solutions .
::从图中可以看出,我们可以看到这四个交叉点或解决办法。

Example 5
::例5

Solve

$\begin{aligned} x^{2} + (y - 1)^{2} & = 36 \\ x^{2} & = 2 (y + 9) . \end{aligned}$
$\begin{align*}x^2+(y-1)^2 &= 36 \\ x^2 &= 2(y+9).\end{align*}$
::溶解 x2+(y- 1) 2=36x2=2(y+9)

Solution: We can also solve systems of equations by using elimination by addition. If we wanted to eliminate the $\begin{align*}x^2\end{align*}$ -terms, we could multiply the 2nd equation by -1, and then add the equations.
::解答: 我们还可以通过加法来解析方程式系统。如果我们想要删除 x2 条件, 我们可以将二等式乘以 - 1, 然后添加方程式。

$\begin{aligned} x^{2} + (y - 1)^{2} & = 36 \\ + \underline{- x^{2} = - 2 (y + 9)} \\ (y - 1)^{2} = - 2 (y + 9) & + 36 \\ 2 (y + 9) + (y - 1)^{2} & = 36 \\ 2 y + 18 + y^{2} - 2 y + 1 & = 36 \\ y^{2} & = 17 \\ y & = \pm \sqrt{17} \approx \pm 4.12 \end{aligned}$
$\begin{align*}\cancel{x^2}+(y-1)^2 &= 36 \qquad \qquad\\ + \underline{\qquad -\cancel{x^2} = \text{-}2(y+9)} \\ (y-1)^2=\text{-}2(y+9)&+36\\ 2(y+9)+(y-1)^2 &=36 \\ 2y+18+y^2-2y+1 &=36 \\ y^2 &= 17 \\ y &= \pm \sqrt{17} \approx \pm 4.12\end{align*}$
::x2+(y- 1)2=36x2=-2(y+9)_(y- 1)2=-2(y+9)+362(y+9)+(y- 1)2=362y+18+y2--2y+1=36y2=17y+17_17}4.12

The corresponding $\begin{align*}x\end{align*}$ -values are:
::相应的x值为:

$\begin{aligned} x^{2} & = 2 (4.12 + 9) x^{2} = 2 (- 4.12 + 9) \\ x^{2} & = 26.25 and x^{2} = 9.76 \\ x & = \pm 5.12 x = \pm 3.12. \end{aligned}$
$\begin{align*}x^2 &= 2(4.12+9) \qquad \qquad \quad x^2= 2(\text{-}4.12+9) \\ x^2 &= 26.25 \qquad \qquad \text{and} \qquad x^2= 9.76 \\ x &= \pm 5.12 \qquad \qquad \qquad \quad \ \ x= \pm 3.12.\end{align*}$
::x2=2(4.12+9)x2=2(4.12+9)x2=(4.12+9)x2=(26.25)x2=(9.76x)=(5.12)x(3.12)。

The solutions are: $\begin{align*}(4.12, 5.12)\end{align*}$ , $\begin{align*}(4.12, \text{-}5.12)\end{align*}$ , $\begin{align*}(\text{-}4.12, 3.12),\end{align*}$ and $\begin{align*}(\text{-}4.12, \text{-}3.12)\end{align*}$ .
::解决办法是4.12,5.12),(4.12,5.12),(4.12,5.12),(4.12,3.12),(4.12,3.12)和(4.12,3.12)。

The circle and the parabola intersect in four places.
::圆和抛物线在四个地方交叉。

by davidtutorsmath shows how to solve a system of equations with elimination.
::通过 davidutorsmath 显示如何用除去来解析方程式系统。

Example 6
::例6

Solve
::解决

$\begin{aligned} x^{2} - y^{2} & = 8 \\ x^{2} + y^{2} & = 12 \end{aligned}$
$\begin{align*}x^2 -y^2&=8 \\ x^2+y^2 &= 12\end{align*}$
::x2- y2=8x2+y2=12

Solution: We can solve this system by elimination by adding the two equations.
::解决方案:我们可以通过添加两个方程式来消除这个系统。

$\begin{aligned} x^{2} - y^{2} = 8 \\ + & \underline{x^{2} + y^{2} = 12} \\ 2 x^{2} = 20 \\ x^{2} = 10 \\ x = \pm \sqrt{10} \approx \pm 3.16 \\ y = \pm \sqrt{12 - x^{2}} = \pm \sqrt{12 - (\sqrt{10})^{2}} = \pm \sqrt{12 - 10} = \pm \sqrt{2} \approx \pm 1.414 \\ y = \pm \sqrt{12 - x^{2}} = \pm \sqrt{12 - (- \sqrt{10})^{2}} = \pm \sqrt{12 - 10} = \pm \sqrt{2} \approx \pm 1.414 \end{aligned}$
$\begin{align*}&x^2-\cancel{y^2}=8 \ \\ + &\underline{\ x^2+\cancel{y^2}=12} \\ &2x^2 = 20 \\ &x^2 =10 \\ &x= \pm \sqrt{10} \approx \pm 3.16 \\ \\ &y= \pm \sqrt{12-x^2} = \pm \sqrt{12-(\sqrt{10})^2}= \pm \sqrt{12-10} = \pm \sqrt{2} \approx \pm 1.414\\ &y= \pm \sqrt{12-x^2} = \pm \sqrt{12-(\text{-}\sqrt{10})^2}= \pm \sqrt{12-10} = \pm \sqrt{2} \approx \pm 1.414\end{align*}$
::x2- y2= 8 + x2+y2= 12_ 2x2= 20x2= 10x10_ 10_ 10_ 3. 16y\\ 12- x2_ 12- (1010) @ 12_ 12_ 12_ 10_ 14_ 14_ 12_ x2_ 12_ (- 10)2_ 12_ 10_ @ @ @ 2: 1414

There are four solutions: $\begin{align*}(3.16, 1.41)\end{align*}$ , $\begin{align*}(3.16, \text{-}1.41)\end{align*}$ , $\begin{align*}(\text{-}3.16, 1.41)\end{align*}$ , and $\begin{align*}(\text{-}3.16, \text{-}1.41)\end{align*}$ .
::有四种解决办法3.16,1.41),(3.16,1.41),(3.16,1.41),(3.16,1.41),(3.16,1.41)和(3.16,1.41)。

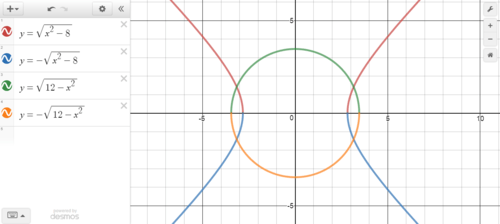
A graph of this system from Desmos is below.
::Desmos提供的此系统图如下。

Notice we have to graph the and the circle in two sections. To find the solutions of the system, we need to check the intersections of each section of the graphs.
::我们必须在两个部分中绘制圆形和圆形图。要找到系统的解决方案,我们需要检查图表每一部分的交叉点。

Example 7
::例7

Solve
::解决

$\begin{aligned} (x - 3)^{2} + (y + 2)^{2} = 4 \\ y = - 4 \end{aligned}$
$\begin{align*}(x-3)^2+(y+2)^2=4 \\ y=\text{-}4\end{align*}$
:x-3)2+(y+2)2=4y=4

Solution: We can solve this using substitution.
::解决办法:我们可以用替代方法解决这个问题。

$\begin{aligned} (x - 3)^{2} + (y + 2)^{2} & = 4 \\ (x - 3)^{2} + (- 4 + 2)^{2} & = 4 \\ (x - 3)^{2} + (- 2)^{2} & = 4 \\ (x - 3)^{2} & = 0 \\ x - 3 & = 0 \\ x & = 3 \end{aligned}$
$\begin{align*}(x-3)^2+(y+2)^2&=4 \\ (x-3)^2+(\text{-}4+2)^2&=4 \\ (x-3)^2+(\text{-}2)^2&=4 \\ (x-3)^2&=0 \\ x-3&=0 \\ x&=3 \\ \end{align*}$
:x-3)2+(y+2)2=4(x-3)2+(4+2)2+(4+2)2=4(x-3)2+(2)2+(2)2=4(x-3)2+4(x-3)2=0x-3=0x=3)

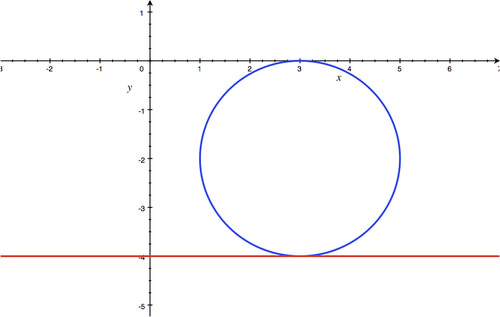
This circle and this line intersect at one point, (3,-4). We can see this on the graph below.
::此圆和此直线在一个点( 3, 4) 交叉。我们可以在下图中看到这一点。

Example 8
::例8

Solve
::解决

$\begin{aligned} \frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 \\ 4 (x - 4) = y^{2} \end{aligned}$
$\begin{align*}\frac{x^2}{4}+\frac{y^2}{9}=1 \\ 4(x-4)=y^2\\\end{align*}$
::x24+y29=14(x-4)=y2

Solution: We can solve this by substitution.
::解决之道:我们可以通过替代来解决这个问题。

$\begin{aligned} \frac{x^{2}}{4} + \frac{4 (x - 4)}{9} & = 1 \\ 36 (\frac{x^{2}}{4} + \frac{4 x - 16)}{9}) & = 1 \cdot 36 \\ 9 x^{2} + 4 (4 x - 16) & = 36 \\ 9 x^{2} + 16 x - 64 & = 36 \\ 9 x^{2} + 16 x - 100 & = 0 \\ x = \frac{- 16 \pm \sqrt{16^{2} - 4 (9) (- 100)}}{2 (9)} \end{aligned}$
$\begin{align*}\frac{x^2}{4}+\frac{4(x-4)}{9}&=1 \\ 36 \bigg( \frac{x^2}{4}+\frac{4x-16)}{9} \bigg) &=1 \cdot 36 \\ 9x^2+4(4x-16) &=36 \\ 9x^2+16x - 64 &= 36 \\ 9x^2+16x - 100 &= 0 \\ \\ x=\frac{\text{-}16 \pm \sqrt{16^2 - 4 (9)(\text{-}100)}}{2(9)} \\\end{align*}$
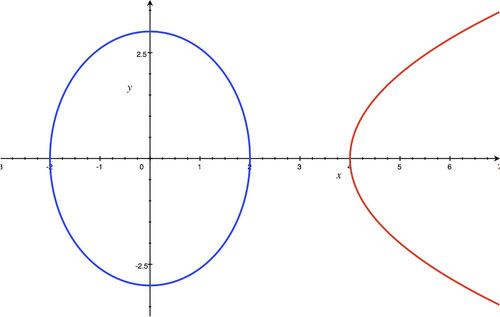
::x24+4(x-4)9=136(x24+4x-169)=1369x2+4(4x-16)=369x2+16x-64=369x2+16x-64=369x2+16x-1000x=16_162-4(9)(-1002(9))

This ellipse and parabola do not intersect. We can see this on the graph below.
::这个椭圆和抛物线没有交叉。我们可以在下面的图表上看到这一点。

Example 9
::例9

A camera business has fixed costs of $4,000, and it costs $100 to produce each camera. The price-demand equation, the price given a number of cameras consumers want to buy, can be modeled by $\begin{align*}p=500-0.125q,\end{align*}$ where $\begin{align*}p\end{align*}$ is the price and $\begin{align*}q\end{align*}$ is the quantity demanded. How many cameras need to be sold to reach what is called the "break-even point," the point at which the costs equal the revenue generated from selling a product?
::摄影机企业固定成本为4000美元,每台摄影机生产成本为100美元。价格需求方程式 — — 给一些消费者想要购买的照相机的价格 — — 可以通过p=500-0.125q(p=500-0.125q)模拟,p是价格,q是所需数量。需要出售多少相机才能达到所谓的“平衡点 ” , 即成本等于销售产品所得收入的点?

Solution: We need to write equations for the cost and the revenue. For the costs, we need $\begin{align*}d\end{align*}$ dollars for the fixed costs and the costs for each camera: $\begin{align*}d=100q+4,\!000\end{align*}$ . The revenue is the price times the quantity, and here the price is modeled in terms of the quantity: $\begin{align*}d=pq=(500-0.125q)q=500q-0.125q^2.\end{align*}$ If we solve the system, we can find the break-even point.
::解答: 我们需要写出成本和收入的方程式。对于成本, 我们需要美元来支付固定成本和每台摄影机的成本: d=100q+4 000。收入是价格乘以数量, 这里的价格是按数量计算的: d=pq=( 500-0.125q)q=500q-0.125q2. 如果我们解决了系统, 我们能找到平衡点。

$\begin{aligned} 100 q + 4, 000 & = 500 q - 0.125 q^{2} \\ 0.125 q^{2} & - 400 q + 4, 000 = 0 \\ q & = \frac{- (- 400) \pm \sqrt{(- 400)^{2} - 4 (0.125) (4, 000)}}{2 (0.125)} \\ = \frac{400 \pm \sqrt{160, 000 - 2, 000}}{0.25} \\ = \frac{400 \pm 397.5}{0.25} \\ = 10 and = 3, 190 \end{aligned}$
$\begin{align*}100q+4,\!000&=500q-0.125q^2 \\ 0.125q^2&-400q+4,\!000=0 \\ \\ q&=\frac{\text{-}(\text{-}400) \pm \sqrt{(\text{-}400)^2 - 4(0.125)(4,\!000)}}{2(0.125)} \\ &=\frac{400 \pm \sqrt{160,\!000 - 2,\!000}}{0.25} \\ &=\frac{400 \pm 397.5}{0.25} \\ &=10 \ \text{and} \ =3,\!190 \end{align*}$
::100q+4 000=500q-0.125q20.125q2-400q+4 000q=0q=-(400)](-400)(-400)2-4(0.125)(4 000)2(0.125)=400160 000-2 000.0.25=400×397.50.25=10和=3,190)

The cost and revenue are equal when 10 cameras are sold and when 3,190 cameras are sold. Since a business will sell 10 cameras before it sells 3,190, the break-even point is 10.
::出售10台照相机和出售3 190台照相机,成本和收入相等,因为企业在出售3 190台摄影机之前出售10台照相机,收支平衡点是10台。

Summary
::摘要

We can solve systems of conic sections by graphing, substitution, and elimination by addition.
::我们可以通过图形绘制、替代和添加消除等方法解决二次曲线部分的系统。

Review
::回顾

Estimate the solutions for each system of equations below.
::估计以下每一方程式系统的解决办法。

1.

2.

3.

4.

Solve each system of equations below.
::解决下方方程式的每一个系统。

5. $\begin{align*}x^2+y^2 &= 7.5 \\ x+2y &= 6\end{align*}$
::5. x2+y2=7.5x+2y=6

6. $\begin{align*}x^2 &= y+4 \\ \frac{x^2}{4}+(y+2)^2 &= 1\end{align*}$
::6. x2=y+4x24+(y+2)2=1

.

7. $\begin{align*}(x-1)^2+(y-3)^2 &= 25 \\ x^2 &= \text{-}2(y-10)\end{align*}$
::7. (x--1)2+(y-3)2=25x2=-2(y-10)

.

8. $\begin{align*}x^2+y^2 &=16 \\ 4x-3y &= 18\end{align*}$
::8. x2+y2=164x--3y=18

.

9. $\begin{align*}(x+4)^2+(y+1)^2 &= 36 \\ \frac{(x+1)^2}{4} + \frac{(y-2)^2}{25} &= 1\end{align*}$
::9. (x+4)2+(y+1)2=36(x+1)24+(y-2)225=1

10. $\begin{align*}4x^2-y^2=8 \\ y^2=x+4\end{align*}$
::10. 4x2-y2=8y2=x+4

Explore More
::探索更多

1. How many different ways can a circle and a parabola intersect? Draw each possibility.
::1. 圆形和抛物线相互交错可采用多少种不同方式?

2. How many different ways can a circle and an ellipse intersect? Draw each possibility.
::2. 圆形和椭圆交叉可采用多少种不同方式? 绘制每一种可能性。

3. Create a system of two circles with no solution. What would the graph look like?
::3. 建立一个没有解决办法的双环系统,图象是什么样子?

4. Find the solutions for the system
::4. 为系统找到解决办法

$\begin{aligned} x^{2} + y^{2} & = r^{2} \\ y & = m x . \end{aligned}$
$\begin{align*}x^2+y^2 &= r^2 \\ y &= mx.\end{align*}$
::x2+y2=r2y=mx.

Leave your answers in terms of $\begin{align*}m\end{align*}$ and $\begin{align*}r\end{align*}$ .
::留下你的答案以m和r。

5. Determine if the system of three equations below have one common solution.
::5. 确定以下三个方程式系统是否有一个共同的解决办法。

$\begin{aligned} x^{2} + 3 y^{2} & = 16 \\ 3 x^{2} + y^{2} & = 16 \\ y & = x \end{aligned}$
$\begin{align*}x^2+3y^2 &= 16 \\ 3x^2+y^2 &= 16 \\ y &= x\end{align*}$
::x2+3y2=163x2+y2=16y=x

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复

Please see the Appendix.
::请参看附录。

章节大纲

Solving Systems of Conic Sections ::二次元件的溶解系统

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Example 9 ::例9

Summary ::摘要

Review ::回顾

Explore More ::探索更多

Answers for Review and Explore More Problems ::回顾和探讨更多问题的答复

Solving Systems of Conic Sections
::二次元件的溶解系统

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Example 8
::例8

Example 9
::例9

Summary
::摘要

Review
::回顾

Explore More
::探索更多

Answers for Review and Explore More Problems
::回顾和探讨更多问题的答复