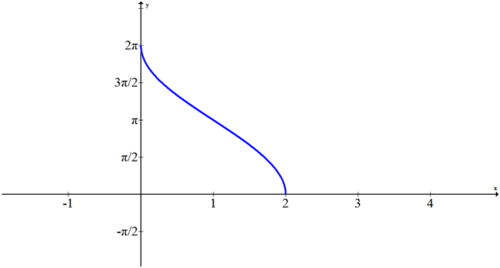
Section: 反向三角函数图 | 7.7 反向三角函数图

Section outline

Introduction
::导言

Have you ever contemplated the ideal spot to sit in a movie theater? Some people like to be as close as possible to the movie, while others prefer a full view from the farthest seat. Some people prefer to sit on an aisle seat, and others in the middle. If a movie theater has a 30-foot-high screen that is 6 feet above eye level, your viewing angle can be modeled by the following equation:

\begin{aligned} θ = \tan^{- 1} \frac{36}{x} - \tan^{- 1} \frac{6}{x} . \end{aligned}

lesson content

Notice in this problem we have an inverse of a tangent, designated by $\begin{aligned} \arctan x \end{aligned}$ or $\begin{aligned} \tan^{- 1} x \end{aligned}$ . This lesson will explore the graphs of inverse trigonometric functions , and will address why $\begin{aligned} \sin^{- 1} (\sin 370^{\circ}) \neq 370^{\circ} \end{aligned}$ .
::在此问题上, 我们有一个相反的正切值, 由 arctanx 或 tan- 1x 指定。此课将探索反三角函数的图解, 并将解答为什么 sin- 1( sin370) 370 。

Inverse Trigonometric Functions
::反逆三角函数

In order for inverses of functions to be functions, the original function must pass the horizontal line test . Recall that the horizontal line test can be used to determine if a function is one-to-one, which is a requirement for a function to have an inverse.
::函数的反函数要成为函数, 原始函数必须通过水平线测试。提醒注意, 水平线测试可用于确定函数是否一对一, 这是函数反向要求的。

Even though none of the trigonometric functions pass the horizontal line test over the entire set of real numbers, their domains can be restricted for the purpose of studying and applying inverses. Inverses are produced by reflecting that portion over $\begin{aligned} y = x, \end{aligned}$ and solving a function $\begin{aligned} f (x) = y \end{aligned}$ for "> $\begin{aligned} f (y) \end{aligned}$ .
::尽管三角函数没有一个能通过横线测试,超过所有实际数字组,但可以限制它们的域,以便研究和应用反向。反向则通过在 y=x 上反映该部分和为 f 解析函数 f(x) =y 来生成。

Consider the sine graph:
::考虑正弦图 :

lesson content

As a general rule, the restrictions to the domain of $\begin{aligned} y = \sin x \end{aligned}$ is the interval $\begin{aligned} [- \frac{π}{2}, \frac{π}{2}] \end{aligned}$ and $\begin{aligned} y = \cos x \end{aligned}$ the interval $\begin{aligned} [0, π] \end{aligned}$ . The 1 st interval is appropriate for sine and cosecant functions, because half of its period is captured, and the graphs still pass the horizontal line test. The sine function restricted to $\begin{aligned} [- \frac{π}{2}, \frac{π}{2}] \end{aligned}$ is shown above. This interval is also appropriate for the tangent function because its entire period is captured, and the graph passes the horizontal line test.
::通常情况下,y=sinx的域限制是间隔 [2, 2] 和y=cosx的间距 [0, ] 。第一个间距适用于正弦和正弦函数, 因为它的期间有一半被记录, 图形仍然通过水平线测试。上文显示的正弦函数仅限于 [2, 2] 。这个间距也适用于正切函数, 因为它的整个期间被记录, 而图形通过水平线测试。

The interval $\begin{aligned} [0, π] \end{aligned}$ is appropriate for cosine, secant, and cotangent functions for the same reasons, because the entire period for these functions is captured and their graphs pass the horizontal line test.
::出于同样的原因,[0] 间隔适合于余弦、分离和共切函数,因为这些函数的整个期间被记录下来,它们的图表通过水平线测试。

Like other functions, t o graph the inverse of a trigonometric function , reflect the restricted portion of the graph across the line $\begin{aligned} y = x \end{aligned}$ . For the sine function above (the red curve), the blue curve below shows $\begin{aligned} f (x) = \sin^{- 1} x \end{aligned}$ :
::与其他函数一样,要绘制三角函数的反形图,则要反映横跨y=x线的图形限制部分。对于上面的正弦函数(红色曲线),下面的蓝色曲线显示 f(x)=sin-1x:

lesson content

The result of this inversion is that arcsine function will only produce angles between and including $\begin{aligned} - \frac{π}{2} \end{aligned}$ and $\begin{aligned} \frac{π}{2} \end{aligned}$ . T hese values are used in context to evaluate a wide group of function values.
::这种反转的结果是, arcsine 函数只产生 2 和 2 之间的角度, 并包括 2 和 2 。这些值用于上下文中评估一系列广泛的函数值。

Examples
::实例

Example 1
::例1

What is the graph of $\begin{aligned} f (x) = \cos^{- 1} x \end{aligned}$ ?
::f( x) =cos- 1\\\ x 的图形是什么 ?

Solution:
::解决方案 :

Graph the portion of cosine that fits the horizontal line test (the interval $\begin{aligned} [0, π] \end{aligned}$ ) and reflect across the line $\begin{aligned} y = x \end{aligned}$ .
::绘制符合水平线测试( 间距 [0, ) 并反射到横线 y=x 的余弦部分。

lesson content

Example 2
::例2

Graph the function $\begin{aligned} f (x) = 2 \cos^{- 1} (x - 1) \end{aligned}$ .
::函数 f( x) = 2cos- 1\\\ (x- 1) 的图形。

Solution:
::解决方案 :

Since the graph of $\begin{aligned} f (x) = \cos^{- 1} x \end{aligned}$ was sketched in Example 1, simply shift it right 1 unit and stretch it vertically by a factor of 2. It intersected the $\begin{aligned} x \end{aligned}$ axis at 1 before, and now it will intersect at 2. It reached a height of $\begin{aligned} π \end{aligned}$ before, and now it will reach a height of $\begin{aligned} 2 π \end{aligned}$ .
::由于F(x)=cos-1x的图形在例1中绘制,只需将它向右移动1个单位,并垂直伸展为2倍。它以前将x轴交叉到1,现在将交叉到2。它以前达到...的高度,现在将达到2的高度。

lesson content

Example 3
::例3

Evaluate the following expression with and without a calculator, using right triangles and the basic inverse trigonometric functions:
::使用右三角形和基本反三角函数,用计算器和非计算器评价下列表达式:

\begin{aligned} \cot (\csc^{- 1} (- \frac{13}{5})) . \end{aligned}

csc-1(-135))。

Solution:
::解决方案 :

Recall that the cosecant is a function that produces an angle of a ratio of a hypotenuse of 13, in this case, and an opposite side of -5. The sine of the inverse ratio must produce the same angle, so start there:
::回想到,共生层是一个函数,产生一个角,即低于13的角,在此情况下,是-5.的对面。反比的正反面必须产生相同的角, 因此从这里开始:

\begin{aligned} \csc^{- 1} (- \frac{13}{5}) = \sin^{- 1} (- \frac{5}{13}) . \end{aligned}

::csc-1(-135)=sin-1(-513)。

Apply $\begin{aligned} \cot (θ) = \frac{1}{\tan θ} \end{aligned}$

\begin{aligned} \cot (\csc^{- 1} (- \frac{13}{5})) = \frac{1}{\tan (\sin^{- 1} (- \frac{5}{13}))} = - \frac{12}{5} . \end{aligned}

::应用 () = 1tan (csc- 1) (- 135) = 1tan (sin- 1) (-513) 125。

Graphically, you can recall that $\begin{aligned} \csc^{- 1} (- \frac{13}{5}) \end{aligned}$ describes an angle in the 4th or 2nd quadrant because those are the two quadrants where cosecant is negative. Since the inverse cosecant function has a range $\begin{aligned} [- \frac{π}{2}, \frac{π}{2}] \end{aligned}$ , it only produces angles in quadrant I or quadrant IV. This reference triangle must then be in the 4th quadrant. Just draw the triangle and identify the cotangent ratio.
::图形化中, 您可以记得 csc- 1 (- 135) 描述第四或第二象方块中的角, 因为这些是两个二次方块, 其共生区块为负。由于反向共生区块函数具有一个范围 [2, 2] , 它只产生一等方块或四等方块中的角。此引用三角块必须位于第四象方块中。只要绘制三角形并确定余切比即可。

lesson content

Example 4
::例4

Return to the Introduction problem: Explain why $\begin{aligned} \sin^{- 1} (\sin 370^{\circ}) \neq 370^{\circ} . \end{aligned}$
::回到引言问题:解释为什么sin -1 {(sin}}370}}}}}}{370}}}}。

Solution:
The initial angle of 370° is not in the restricted domain of $\begin{aligned} [- 90^{\circ}, 90^{\circ}] \end{aligned}$ . However, the resulting angle of the inverse sine of sine of 370° will fall in this restricted domain. Thus, the left and right sides of the given equation are not equal.
::解答: 370°的初始角度不在[- 90, 90] 的限制范围内。但是, 由此得出的正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正弦正正弦正弦方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方方

Example 5
::例5

What is the graph of $\begin{aligned} y = \tan^{- 1} x \end{aligned}$ ?
::您的图是什么 y=tan - 1x ?

Solution:
::解决方案 :

Graph the portion of tangent that fits the horizontal line test and reflect across the line $\begin{aligned} y = x \end{aligned}$ . Note that the graph of the inverse tangent function is in blue.
::绘制符合水平线测试并反射到横线 y=x 的正切值部分。请注意反正切值的图形是蓝色的。

lesson content

Example 6
::例6

What is the graph of $\begin{aligned} y = \csc^{- 1} x \end{aligned}$ ?
::y=csc-1x的图表是什么?

Solution:
::解决方案 :

Graph the portion of cosecant that fits the horizontal line test and reflect across the line $\begin{aligned} y = x \end{aligned}$ .
::绘制符合水平线测试并反射到横线 y=x 的 cosecant 部分。

lesson content

Note that $\begin{aligned} f (x) = \csc^{- 1} x \end{aligned}$ is the added portion in blue.
::注意 f( x) = csc- 1 x 是蓝色的附加部分。

Example 7
::例7

Evaluate the expression $\begin{aligned} \csc (\cot^{- 1} [- \frac{8}{6}]) \end{aligned}$ .
::评估 csc(cot- 1[-86]) 表达式。

Solution:
::解决方案 :

Note that $\begin{aligned} \csc x = \frac{1}{\sin x} \end{aligned}$ and $\begin{aligned} \cot^{- 1} (\frac{a}{b}) = \tan^{- 1} (\frac{b}{a}) \end{aligned}$ .
::注意 cscx = 1sinx 和 cot- 1(ab) =tan- 1(ba) 。

\begin{aligned} \csc (\cot^{- 1} [- \frac{8}{6}]) & = \frac{1}{\sin (\cot^{- 1} [- \frac{8}{6}])} \\ = \frac{1}{\sin (\tan^{- 1} (- \frac{6}{8}))} \\ = - \frac{10}{6} \\ = - \frac{5}{3} \end{aligned}

::csc(cot-1(-86)=1sin(cot-1(-86))=1sin(tan-1(-68))10653

Summary
::摘要

Even though none of the trigonometric functions pass the horizontal line test over the entire set of real numbers, their domains can be restricted for the purpose of studying and applying inverses.
::即使三角函数没有一个能通过横线测试,超过整个一套实际数字,但为了研究和应用反向,它们的域可以加以限制。

There are two conventions used to identify inverse trigonometric functions: using the prefix of arc or the superscript of -1.
::有两项公约用来确定反三角函数:使用弧的前缀或-1的上标。

A summary of the domains and ranges of all the inverse trig functions:
::所有反三角函数的域和范围摘要 :

Notation 1	Notation 2	Definition	Domain	Range
$\begin{aligned} y = \arcsin x \end{aligned}$	$\begin{aligned} y = {s i n}^{- 1} (x) \end{aligned}$	$\begin{aligned} x = \sin y \end{aligned}$	[-1, 1]	$\begin{aligned} [- \frac{π}{2}, \frac{π}{2}] \end{aligned}$
$\begin{aligned} y = \arccos x \end{aligned}$	$\begin{aligned} y = {c o s}^{- 1} (x) \end{aligned}$	$\begin{aligned} x = \cos y \end{aligned}$	[-1, 1]	$\begin{aligned} [0, π] \end{aligned}$
$\begin{aligned} y = \arctan x \end{aligned}$	$\begin{aligned} y = {t a n}^{- 1} (x) \end{aligned}$	$\begin{aligned} x = \tan y \end{aligned}$	$\begin{aligned} (- \infty, \infty) \end{aligned}$	$\begin{aligned} (- \frac{π}{2}, \frac{π}{2}) \end{aligned}$
$\begin{aligned} y = arc \cot x \end{aligned}$	$\begin{aligned} y = {c o t}^{- 1} (x) \end{aligned}$	$\begin{aligned} x = \cot y \end{aligned}$	$\begin{aligned} (- \infty, \infty) \end{aligned}$	$\begin{aligned} (0, π) \end{aligned}$
$\begin{aligned} y = arc \csc x \end{aligned}$	$\begin{aligned} y = {c s c}^{- 1} (x) \end{aligned}$	$\begin{aligned} x = \csc y \end{aligned}$	$\begin{aligned} (- \infty, - 1] ⋃ [1, \infty) \end{aligned}$	$\begin{aligned} (- \frac{π}{2}, 0) ⋃ (0, \frac{π}{2}) \end{aligned}$
$\begin{aligned} y = arc \sec x \end{aligned}$	$\begin{aligned} y = {s e c}^{- 1} (x) \end{aligned}$	$\begin{aligned} x = \sec y \end{aligned}$	$\begin{aligned} (- \infty, - 1] ⋃ [1, \infty) \end{aligned}$	$\begin{aligned} (0, π) \end{aligned}$

Review
::回顾

1. Graph $\begin{aligned} f (x) = \cot^{- 1} x \end{aligned}$ .
::1. 图f(x)=cot-1x。

2. Graph $\begin{aligned} g (x) = \sec^{- 1} x \end{aligned}$ .
::2. 图g(x)=sec-1x。

Name each of the following graphs:
::列出下列每个图表:

lesson content

Graph each of the functions using function transformations:
::使用函数变换的函数图 :

8. $\begin{aligned} h (x) = 3 \sin^{- 1} (x + 1) \end{aligned}$
::8. h(x) = 3sin- 1 (x+1)

9. $\begin{aligned} k (x) = 2 \sin^{- 1} (x) + \frac{π}{2} \end{aligned}$
::9. k(x) = 2sin - 1 (x) 2

10. $\begin{aligned} m (x) = - \cos^{- 1} (x - 2) \end{aligned}$
::10. m(x) cos- 1(x-2)

11. $\begin{aligned} j (x) = \cot^{- 1} (x) + π \end{aligned}$
::11. j(x) = Cot-1(x)

12. $\begin{aligned} p (x) = - 2 \tan^{- 1} (x - 1) \end{aligned}$
::12.p(x)%%2tan-1(x-1)

13. $\begin{aligned} q (x) = \csc^{- 1} (x - 2) \end{aligned}$
::13. q(x) = csc- 1 (x-2)

14. $\begin{aligned} r (x) = - \sec^{- 1} (x) + 4 \end{aligned}$
::14. r(x)sec-1(x)+4

15. $\begin{aligned} t (x) = \csc^{- 1} (x + 1) - \frac{3 π}{2} \end{aligned}$
::15. t (x) = csc- 1 (x+1) - 32

16. $\begin{aligned} v (x) = 2 \sec^{- 1} (x + 2) + \frac{π}{2} \end{aligned}$
::16. v(x)=2sec-1(x+2)=2sec-1(x+2)=2

17. $\begin{aligned} w (x) = - \cot^{- 1} (x) - \frac{π}{2} \end{aligned}$
::17. w(x)_________________________________________________________________________________________________________________________________________________________________________________

Evaluate each expression:
::评估每个表达式:

18. $\begin{aligned} \sec (\tan^{- 1} [\frac{3}{4}]) \end{aligned}$
::18 秒( tan-1[ 34])

19. $\begin{aligned} \cot (\csc^{- 1} [\frac{13}{12}]) \end{aligned}$
::19. ot(csc-1[1312])

20. $\begin{aligned} \csc (\tan^{- 1} [\frac{4}{3}]) \end{aligned}$
::20. csc(tan-1[43])

Review (Answers)
::回顾(答复)

Please see the Appendix.
::请参看附录。

Section outline

Introduction ::导言

Inverse Trigonometric Functions ::反逆三角函数

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers) ::回顾(答复)

Introduction
::导言

Inverse Trigonometric Functions
::反逆三角函数

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers)
::回顾(答复)