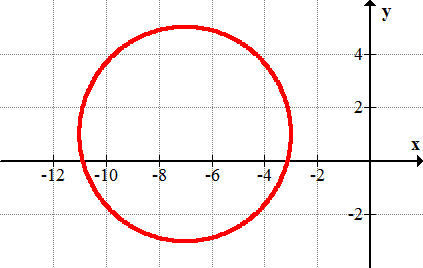节: 圆环 | 11.4 圆圈 | The Way To Learn

章节大纲

Introduction
::导言

A circle is the collection of points that are the same distance from a single point. What is the connection between the Pythagorean Theorem and a circle?
::一个圆是一个圆的集合点,与一个点的距离相同。 Pytagoren Theorem 和一个圆之间有什么联系?

The Circle
::圆圈

Recall that a circle is generated when a plane is perpendicular to the axis of the cone. As a result, a circle is the collection of points that are equidistant from a single point. This single point is called the center of the circle. A circle does not have a focus or a directrix, instead it simply has a center.
::提醒注意当一平面与锥体轴垂直时会生成一个圆。因此, 一个圆就是从一个点收集相距相等的点。这个单点被称为圆的中心。一个圆没有焦点或直线, 而只是有一个中心。

Circles can be recognized immediately from the general equation of a conic when the coefficients of $\begin{aligned} x^{2} \end{aligned}$ and $\begin{aligned} y^{2} \end{aligned}$ are the same sign and the same value. Circles are not functions because they do not pass the vertical line test. The distance from the center of a circle to the edge of the circle is called the radius of the circle. The distance from one end of the circle through the center to the other end of the circle is called the diameter. The diameter is equal to twice the radius.
::当 x2 和 y2 的系数是相同的符号和值时,可以从二次曲线的普通方程式中立即识别圆圈。圆圈不是函数,因为它们没有通过垂直线测试。圆圈中心到圆圈边缘的距离称为圆圈半径。圆圈一端到圆圈另一端的距离称为直径。直径等于半径的两倍。

The graphing form of a circle is $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} . \end{aligned}$ The center of the circle is at $\begin{aligned} (h, k), \end{aligned}$ and the radius of the circle is $\begin{aligned} r \end{aligned}$ . Note that this looks remarkably like the Pythagorean Theorem.
::圆的图形形式是 (x-h) 2+(y-k)2=r2. 圆的中心在 k,圆的半径是 r。请注意, 这与 Pytagorean 理论非常相似。

Standard Form of the Equation of a Circle
::圆形等量的标准格式

$\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2}, \end{aligned}$

:x-h)2+(y-k)2=r2,

where $\begin{aligned} (h, k) \end{aligned}$ is the center of the circle and $\begin{aligned} r \end{aligned}$ is the radius.
::其中 (h, k) 是圆的中心, r 是圆的半径。

The following video explains how to graph a circle in standard form and general form:
::以下视频解释如何以标准形式和一般形式绘制圆形图:

Play, Learn, and Explore Circles:
::玩耍、学习和探索圆圈:

Examples
::实例

Example 1
::例1

Graph the following circle:
$\begin{aligned} (x - 1)^{2} + (y + 2)^{2} = 9. \end{aligned}$

::如下圆形图解x- 1) 2+(y+2) 2=9。

Solution:
::解决方案 :

Plot the center and the four points that are exactly 3 units from the center.
::绘制中间点和四个点正好是中间的3个单位

Example 2
::例2

Translate the following conic from standard form to graphing form. Identify the center and the radius.
$\begin{aligned} 36 x^{2} + 36 y^{2} - 24 x + 36 y - 275 = 0 \end{aligned}$

::将以下二次曲线从标准窗体转换为图形化窗体。识别中心及半径 36x2+36y2- 24x+36- 275=0

Solution:
::解决方案 :

Complete the square and then divide by the coefficient of $\begin{aligned} x^{2} \end{aligned}$ and $\begin{aligned} y^{2} \end{aligned}$ .
::完成方形,然后除以 x2 和 y2 的系数。

$\begin{aligned} 36 x^{2} - 24 x + 36 y^{2} + 36 y = 275 \\ 36 (x^{2} - \frac{2}{3} x + \underline{}) + 36 (y^{2} + y + \underline{}) = 275 \\ 36 (x^{2} - \frac{2}{3} x + \frac{1}{9}) + 36 (y^{2} + y + \frac{1}{4}) = 275 + 4 + 9 \\ 36 {(x - \frac{1}{3})}^{2} + 36 {(y + \frac{1}{2})}^{2} = 288 \\ {(x - \frac{1}{3})}^{2} + {(y + \frac{1}{2})}^{2} = 8 \end{aligned}$

::36x2- 24x+3624x+36y2+36y=27536(x2- 23x)+36(y2+y)=27536(x2- 23x+19)+36(y2+y+y+14)=275+4+936(x- 13)2+36(y+12)2=288(x- 13)2+(y+12)2=8

The center is $\begin{aligned} (\frac{1}{3}, - \frac{1}{2}) \end{aligned}$ . The radius is $\begin{aligned} \sqrt{8} = 2 \sqrt{2} \end{aligned}$ .
::中心是(13,-12),半径是8=22。

Example 3
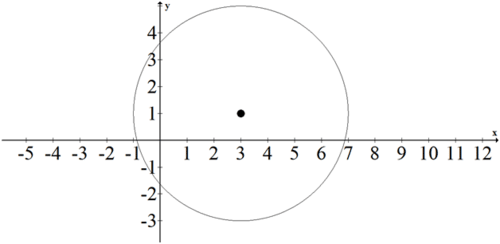
::例3

Write the equation of the following circle:
::写入以下圆形的方程式 :

Solution:
::解决方案 :

The center of the circle is at (3, 1), and the radius of the circle is $\begin{aligned} r = 4 \end{aligned}$ . The equation is $\begin{aligned} (x - 3)^{2} + (y - 1)^{2} = 16 \end{aligned}$ .
::圆的中心是 (3, 1) ,圆的半径是 r=4。方程式是 (x-3) 2+(y- 1) 2=16 。

Example 4
::例4

Recall the question from the Introduction: W hat is the connection between the Pythagorean Theorem and a circle?
::回顾导言中的问题:毕达哥里安神话和圆圈之间有什么联系?

Solution:
::解决方案 :

The reason why the graphing form of a circle looks like the Pythagorean Theorem is because each $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ coordinate along the outside of the circle forms a perfect right triangle with the radius as the hypotenuse.
::圆形的图形形式看起来像毕达哥里安定理词的原因在于每个 x 和 y 在圆圈的外部坐标形成一个完美的右三角形, 半径作为下限。

Example 5
::例5

Graph the following conic section:
$\begin{aligned} (x + 2)^{2} + (y - 1)^{2} = 1. \end{aligned}$

::如下二次曲线区域图解 : (x+2) 2+(y- 1) 2= 1。

Solution:
::解决方案 :

Example 6
::例6

Translate the following conic from standard form to graphing form:
::将以下二次曲线从标准格式转换为图形格式:

$\begin{aligned} x^{2} - 34 x + y^{2} + 24 y + \frac{749}{2} = 0. \end{aligned}$

::x2-34x+Y2+24y+7492=0。

Solution:
::解决方案 :

$\begin{aligned} x^{2} - 34 x + y^{2} + 24 y + \frac{749}{2} & = 0 \\ x^{2} - 34 x + y^{2} + 24 y & = - \frac{749}{2} \\ x^{2} - 34 x + 289 + y^{2} + 24 y + 144 & = - \frac{749}{2} + 289 + 144 \\ (x - 17)^{2} + (y + 12)^{2} & = \frac{117}{2} \end{aligned}$

::x2- 34x+y2+24y+7492=0x2- 34x+y2+24y7492x2x-34x+289+y2+24y+144}}_7492+289+144(x-17)2+(y+12)2=1172

Example 7
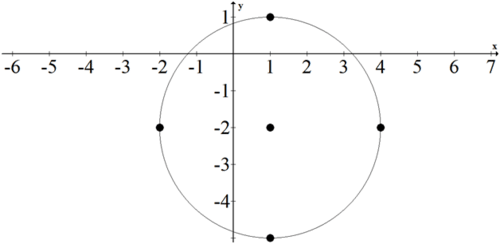
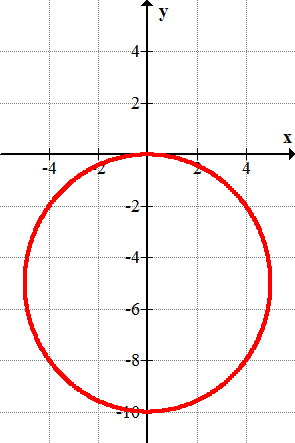
::例7

Write the equation for the following circle:
::写入以下圆形的方程 :

Solution:
::解决方案 :

Note key information from the graph. The center of the circle is located at (1, -2). The radius of the circle is 2. Substitute these key points into the general equation $\begin{aligned} (x - h)^{2} + (y - k)^{2} = r^{2} \end{aligned}$ .
::从图形中注意关键信息。圆的中心位置是(1, - 2),圆的半径是 2. 将这些关键点替换为一般方程(x-h)2+(y-k)2=r2。

The equation of this graph will be $\begin{aligned} (x - 1)^{2} + (y + 2)^{2} = 4 \end{aligned}$ .
::此图的方程式将为 (x-1) 2+(y+2) 2= 4。

Summary
::摘要

A circle is the collection of points that are equidistant from a given point.
::a 圆是指从给定点收集相等于某一点的点数。

The radius of a circle is the distance from the center of the circle to the outside edge.
::圆的半径是从圆的中心到外部边缘的距离。

The center of a circle is the point that defines the location of the circle.
::圆的中心是确定圆位置的点。

The standard equation of a circle is

where

is the center of the circle and

is the radius.
::圆的标准方程式是圆的中心位置,是圆的半径。

Review
::回顾

Graph the following conics:
::图形如下二次曲线:

1. $\begin{aligned} (x + 4)^{2} + (y - 3)^{2} = 1 \end{aligned}$
::1. (x+4)2+(y-3)2=1

2. $\begin{aligned} (x - 7)^{2} + (y + 1)^{2} = 4 \end{aligned}$
::2. (x-7)2+(y+1)2=4

3. $\begin{aligned} (y + 2)^{2} + (x - 1)^{2} = 9 \end{aligned}$
::3. (y+2)2+(x-1)2=9

4. $\begin{aligned} x^{2} + (y - 5)^{2} = 8 \end{aligned}$
::4. x2+(y-5-5)2=8

5. $\begin{aligned} (x - 2)^{2} + y^{2} = 16 \end{aligned}$
::5. (x-2)2+y2=16

Translate the following conics from standard form to graphing form:
::将以下二次曲线从标准格式转换为图形格式:

6. $\begin{aligned} x^{2} - 4 x + y^{2} + 10 y + 18 = 0 \end{aligned}$
::6. x2-4x+y2+10y+18=0

7. $\begin{aligned} x^{2} + 2 x + y^{2} - 8 y + 1 = 0 \end{aligned}$
::7. x2+2x+y2-8y+1=0

8. $\begin{aligned} x^{2} - 6 x + y^{2} - 4 y + 12 = 0 \end{aligned}$
::8. x2-6x+y2-4y+12=0

9. $\begin{aligned} x^{2} + 2 x + y^{2} + 14 y + 25 = 0 \end{aligned}$
::9. x2+2x+y2+14y+25=0

10. $\begin{aligned} x^{2} - 2 x + y^{2} - 2 y = 0 \end{aligned}$
::10. x2-2x+y2-2y=0

Write the equations for the following circles:
::写下下列圆形的方程 :

11.

12.

13.

14.

15.

Review (Answers )
::回顾(答复)

Please see the Appendix.
::请参看附录。

章节大纲

Introduction ::导言

The Circle ::圆圈

Standard Form of the Equation of a Circle ::圆形等量的标准格式

Examples ::实例

Summary ::摘要

Review ::回顾

Review (Answers ) ::回顾(答复)

Introduction
::导言

The Circle
::圆圈

Standard Form of the Equation of a Circle
::圆形等量的标准格式

Examples
::实例

Summary
::摘要

Review
::回顾

Review (Answers )
::回顾(答复)