参数等量的应用

播放段落

Introduction
::导言

播放段落

A regular function has the ability to graph the height of an object over time. allow you to actually graph the complete position of an object over time. For example, parametric equations allow you to make a graph that represents the position of a point on a Ferris wheel. All the details like height off the ground, direction, and speed of spin can be modeled using the parametric equations.
::普通函数能够绘制一个对象随时间推移的高度。允许您实际绘制一个对象随时间推移的完整位置。例如,参数方程式允许您绘制一个图形,以显示Ferris轮上某个点的位置。所有细节,如在地面上高度、方向和旋转速度,都可以用参数方程式模拟。

播放段落

What is the position, equation, and graph of a point on a Ferris wheel that starts at a low point of 6 feet off the ground, spins counterclockwise to a height of 46 feet off the ground, then goes back down to 6 feet in 60 seconds?
::在离地6英尺的低点, 逆时针旋转到离地46英尺的高点, 然后在60秒后又回到6英尺?

 

播放段落

Applications of Parametric Equations
::参数等量的应用

播放段落

Two types of parametric equations are typical in real-life situations: The 1st is circular motion as was described in the concept problem. The 2nd is projectile motion.
::两种参数等式在现实环境中是典型的:第一是概念问题中所描述的循环运动。第二是投射运动。

播放段落

Parametric equations that describe circular motion will have $\begin{align*}x\end{align*}$  and  $\begin{align*}y\end{align*}$  as periodic functions of sine and cosine. Either  $\begin{align*}x\end{align*}$ will be a sine function and $\begin{align*}y\end{align*}$  will be a cosine function, or the other way around. The best way to come up with parametric equations for these situations is to first draw a picture of the circle you are trying to represent.
::描述循环运动的参数方程式将具有x 和 y 作为正弦和正弦的周期函数。 要么 x 将是一个正弦函数, y 将是一个正弦函数, 反之则是一个正弦函数。 为这些情况提出参数方程式的最佳方法是首先绘制您试图代表的圆形图。

播放段落

Next, it is important to note the starting point, center point, and direction. You should already have the graphs of sine and cosine memorized, so that when you see a pattern in words or as a graph, you can identify what you see as + sine, -  sine, + cosine, and -  cosine. In this example, the vertical component starts at a low point of 6, travels to a middle point of 26, up to a height of 46, and then back down. This is a - cosine pattern. The amplitude of the - cosine graph is 20, and the vertical shift is 26. Lastly, the period is 60. You can use the period to help you find $\begin{align*}b.\end{align*}$
::接下来,必须注意起点、中点和方向。 您应该已经拥有正弦图和正弦图和正弦图, 这样当您在文字或图表中看到一个模式时, 您可以识别您所看的 +正弦图、 - 正弦图、 + 正弦图和- 顺弦图。 在此示例中, 垂直元件开始于6 的低点, 向26 的中点移动, 最高为46, 然后向下返回。 这是正弦图。 这是正弦图的振幅是 20, 垂直移动是 26 。 最后, 时段是 60 。 您可以使用该时段来帮助您找到 b 。

播放段落

$$\begin{align*}60 &=\frac{2\pi}{b} \\ b &=\frac{\pi}{30}\end{align*}$$
::60=230

播放段落

Thus, the vertical parameterization is
::因此,垂直参数化是:

播放段落

$$\begin{align*}y=-20 \cos \left(\frac{\pi}{30}t\right)+26.\end{align*}$$
::y20cos(30t)+26。

播放段落

Try to find the horizontal parameterization on your own. The solution will be discussed when we revisit this problem later.
::尝试自己找到水平参数化。 当我们稍后重新讨论这个问题时, 将会讨论解决方案 。

播放段落

Projectile motion has a vertical component that is quadratic and a horizontal component that is linear . This is because there are three parameters that influence the position of an object in flight: starting height, initial velocity, and force of gravity. The horizontal component is independent of the vertical component. This means that gravity doesn't affect it and the starting horizontal velocity will remain the horizontal velocity for the entire flight of the object.
::投影运动有一个垂直的成份是二次形的,一个水平的成份是线性的。 这是因为有三个参数影响着一个物体在飞行中的位置: 起始高度、 初始速度和重力。 水平的成份独立于垂直成份。 这意味着引力不会影响它, 开始的水平速度将保持物体整个飞行的水平速度 。

播放段落

Note that gravity, $\begin{align*}g,\end{align*}$  has a force of about  $\begin{align*}-32 \ ft/s^2 \end{align*}$  or  $\begin{align*}-9.81 \ m/s^2.\end{align*}$  The examples and practice questions in this concept will use feet.
::注意重力(g)的威力大约为-32立方英尺/秒2或-9.81米/秒2。

播放段落

If an object is launched from the origin at a velocity of  $\begin{align*}v,\end{align*}$  then it has horizontal and vertical components that can be found using basic trigonometry.
::如果一个物体以 v 的速率从源头发射,则该物体具有使用基本三角测量法可以找到的横向和纵向组成部分。

播放段落

$$\begin{align*}\sin \theta &=\frac{v_V}{v} \rightarrow v \cdot \sin\theta=v_V \\ \cos\theta &=\frac{v_H}{v} \rightarrow v \cdot \cos\theta=v_H\end{align*}$$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}我...

播放段落

The horizontal component is basically finished. The only adjustments that would have to be made are if the starting location is not at the origin, wind is added, or the projectile travels to the left instead of the right. (See Example 1, below.)
::水平部分基本上已完成。 唯一必须作出的调整是,起始位置不是原点,风是增加的,或投射体向左而不是向右移动。 (见下文例1。 )

播放段落

$$\begin{align*}x=t \cdot v \cdot \cos\theta+h, \text{ where }h \text{ is the initial }x \text{-position}\end{align*}$$
::x=tvcosh, 其中 h 是初始 x 位置

播放段落

The vertical component also needs to include gravity and the starting height. The general equation for the vertical component is
::垂直元件还需要包括重力和起始高度。

播放段落

$$\begin{align*}y=\frac{1}{2} \cdot g \cdot t^2 + t \cdot v \cdot \sin\theta + k.\end{align*}$$
::y"12"g"t2+t"v"sin"k。 y"12"g"t"2+"sin"k。

播放段落

The constant  $\begin{align*}g\end{align*}$  represents the acceleration due to gravity,  $\begin{align*}t\end{align*}$  represents time, $\begin{align*}v\end{align*}$  represents initial velocity, and $\begin{align*}k\end{align*}$  represents starting height. You will explore this equation further in calculus and physics. Note that in this concept, most answers will be found and confirmed using technology such as your graphing calculator.
::常数 g 表示重力加速, t 表示时间, v 表示初始速度, k 表示起始高度。 您可以在微积分和物理中进一步探索这个方程式。 请注意, 在这一概念中, 多数答案会使用您的图形计算器等技术找到和确认 。

播放段落

The video below  explains how to determine the equation that models the height of a person on a Ferris wheel, and the times when a person is at a specific height. 
::下面的视频解释如何确定计算Ferris轮上一个人身高的方程,以及一个人身处特定身高的时间。

 

 

播放段落

The following video  demonstrates applications of parametric equations:
::以下视频展示了参数等式的应用:

 

 

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

A ball is thrown from the point (30, 5) at an angle of $\begin{align*}\frac{4\pi}{9}\end{align*}$ to the left, at an initial velocity of  $\begin{align*}68 \ ft/s.\end{align*}$  Model the position of the ball over time using parametric equations. Use your graphing calculator to graph your equations for the 1st four seconds that the ball is in the air.
::从点(30, 5) 向左4°9角度投出一个球, 最初速度为68英尺/秒。 使用参数方程式来模拟球在时间上的方位。 使用您的图形计算器来绘制球在空中的第1 4 秒的方程式 。

播放段落

Solution:  
::解决方案 :

播放段落

The horizontal component is  $\begin{align*}x=-t \cdot 68 \cdot \cos(\frac{4\pi}{9})+30.\end{align*}$  Note the negative sign because the object is traveling to the left, and the +30 because the object starts at (30, 5).
::水平组件为 xt68cos( 49) +30。 注意负符号, 因为对象向左移动, 而 +30 则因为对象起始于 30, 5 时 。

播放段落

The vertical component is $\begin{align*}y=\frac{1}{2} \cdot (-32) \cdot t^2+t \cdot 68 \cdot \sin (\frac{4\pi}{9})+5.\end{align*}$ Note that $\begin{align*}g=-32\end{align*}$ because gravity has a force of  $\begin{align*}-32 \ ft/s^2,\end{align*}$  and the $\begin{align*}+5\end{align*}$ because the object starts at (30, 5).
::垂直元件为y=12(- 32)t2+t68sin(-49)+5. 请注意,g32,因为重力的强度为-32 ft/s2,而+5,因为天体起始于(30,5)时。

播放段落

Example 2
::例2

播放段落

When does the ball from Example 1 reach its maximum, and when does the ball hit the ground? How far did the person throw the ball?
::例1的球何时达到最大,球何时击中地面?投球的人投球多远?

播放段落

Solution:
::解决方案 :

播放段落

To find when the function reaches its maximum, you can find the vertex of the parabola . Use your calculator to approximate the maximum after you have graphed it. Depending on how small you make your $\begin{align*}T_{step},\end{align*}$  you should find the maximum height to be about 75 feet.
::要找到函数达到最大值时,您可以找到抛物线的顶点。在您绘制图后,使用计算器接近最大值。根据您绘制的Tstep大小,您应该找到最高高度为75英尺左右。

播放段落

To find out when the ball hits the ground, you can set the vertical component equal to zero and solve the quadratic equation. You can also use the table feature on your calculator to determine when the graph goes from having a positive vertical value to a negative vertical value. The benefit for using the table is that it simultaneously tells you the $\begin{align*}x\end{align*}$ -value of the zero.
::要发现球击中地面时,您可以设置等于零的垂直元件并解析二次方程。您也可以使用计算器上的表格特性来确定图形从正垂直值变为负垂直值的时间。使用表格的好处是它同时告诉您零的X值。

播放段落

After about 4.2588 seconds, the ball hits the ground at (-20.29, 0). This means the person threw the ball from (30, 5) to (-20.29, 0), a horizontal distance of just over 50 feet.
::在大约4.2588秒后,球击中地面(20.29,0),这意味着球从(30,5)扔到(20.29,0),水平距离略高于50英尺。

播放段落

Example 3
::例3

播放段落

Kieran is on a Ferris wheel, and his position is modeled by these parametric equations:
::基兰在Ferris轮上, 他的位置以这些参数方程式为模型:

播放段落

$$\begin{align*}x_K &=10 \cdot \cos \left(\frac{\pi}{5}t \right) \\ y_K &=10 \cdot \sin \left(\frac{\pi}{5}t \right)+65\end{align*}$$
::xK=10cos( 5°5t)yK=10sin( 5°5t)+65

播放段落

Jason throws the ball modeled by the equation in Example 1 towards Kieran, who can catch the ball if it gets within three feet. Does Kieran catch the ball?
::杰森把以例1的方程式为模型的球扔到基兰,如果球在三英尺内,谁能抓住球。基兰能抓住球吗?

播放段落

Solution:
::解决方案 :

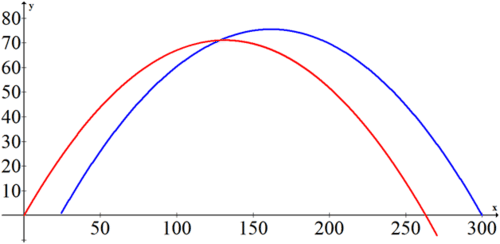
播放段落

This question is designed to demonstrate the power of your calculator. If you simply model the two equations simultaneously and ignore time, you will see several points of intersection . This graph is shown below on the left. These intersection points are not interesting because they represent where Kieran and the ball are at the same place, but at different moments in time. 
::这个问题旨在展示您的计算器的力量。 如果您只是同时模拟两个方程式并忽略时间, 您将会看到多个交叉点。 此图在左侧显示。 这些交叉点并不有趣, 因为它们代表基兰和球位于同一位置, 但是在不同的时间点 。

播放段落

When the $\begin{align*}T_{max}\end{align*}$ is adjusted to 2.3 so that each graph represents the time from 0 to 2.3, you get a better sense that at about 2.3 seconds, the two points are close. This graph is shown above on the right.
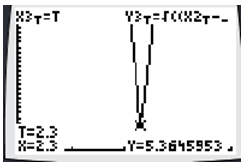
::当Tmax调整为2.3时,每个图表代表0到2.3的时间,你就会更清楚地感觉到,在2.3秒左右,两点接近。这个图表在右边显示。

播放段落

You can now use your calculator to help you determine if the distance between Kieran and the ball actually does go below 3 feet. Start by plotting the ball's position in your calculator as $\begin{align*}x_1\end{align*}$  and  $\begin{align*}y_1,\end{align*}$  and Kieran's position as $\begin{align*}x_2\end{align*}$   and  $\begin{align*}y_2.\end{align*}$ Then, plot a new parametric equation that compares the distance between these two points over time. You can put this under  $\begin{align*}x_3\end{align*}$  and  $\begin{align*}y_3.\end{align*}$  Note that you can find the $\begin{align*}x_1, x_2, y_1, y_2\end{align*}$  entries in the VARS under Y-VARS  and the parametric menu.
::现在您可以使用您的计算器来帮助您确定基兰与球之间的距离是否真的低于3英尺。 从您计算器中的球位置为 x1 和 y1, 基兰的位置为 x2 和 y2 开始, 然后绘制一个新的参数方程, 比较这两个点之间的距离。 您可以将其置于 x3 和 y3 之下 。 请注意, 您可以在 Y- VARS 和 参数菜单下找到 VARS 中的 x1, x2, y1, y2 条目 。

播放段落

$$\begin{align*}x_3 &=t \\ y_3 &=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\end{align*}$$
::x3=ty3(x2- x1)2+(y2-y1)2

播放段落

Now when you graph, you should change your window settings and let $\begin{align*}t\end{align*}$  vary between 0 and 4, the $\begin{align*}x\end{align*}$  window show between 0 and 4, and the  $\begin{align*}y\end{align*}$  window show between 0 and 5. This way it should be clear if the distance truly does get below 3 feet.
::当您图形时, 您应该更改窗口设置, 并在 0 和 4 之间更改, x 窗口显示在 0 和 4 之间, y 窗口显示在 0 和 5 之间 。 这样一来, 如果距离真的低于 3 英尺, 距离应该很明显 。

播放段落

Depending on how accurate your $\begin{align*}T_{step}\end{align*}$  is, you should find that the distance drops below 3 feet. Kieran does indeed catch the ball.
::基兰确实抓住了球

播放段落

Example 4
::例4

播放段落

Recall the question from the Introduction: W hat is the position equation and graph of a point on a Ferris wheel that starts at a low point of 6 feet off the ground, spins counterclockwise to a height of 46 feet off the ground, then goes back down to 6 feet in 60 seconds?
::回顾导言中的问题:在离地6英尺的低点开始,逆时针旋转到离地46英尺的高点,然后在60秒后返回到6英尺的Ferris轮上一个点的位置方程和图是什么?

播放段落

Solution:
::解决方案 :

播放段落

The parametric equations for the point on the wheel are:
::轮子上点的参数方程是:

播放段落

$$\begin{align*}x &=20 \sin \left(\frac{\pi}{30} t \right) \\ y &=-20 \cos \left(\frac{\pi}{30} t \right) +26\end{align*}$$
::x=20sin( °30t) y @ @% 20cos( °30t) +26

播放段落

The horizontal parameterization is found by noticing that the $\begin{align*}x\end{align*}$  values start at 0, go up to 20, go back to 0, then down to -20, and finally back to 0. This is a + sine pattern with amplitude 20. The period is the same as with the vertical component.
::水平参数化通过注意到x值从 0 开始, 向上到 20, 向上到 0, 向下到 - 20, 最后再向上到 0 。 这是一个有振幅 20 的正弦图案 。 时间段与垂直元件相同 。

播放段落

Example 5
::例5

播放段落

At what velocity does a football need to be thrown at a  $\begin{align*}45^\circ\end{align*}$  angle in order to make it all the way across a football field? Assume the person at the other end of the field is catching at the same height as the person throwing the ball.
::为了让足球横跨足球场,需要将足球投向45°C角度的速度如何?假设球场另一端的人与投球的人高度相同。

播放段落

Solution:
::解决方案 :

播放段落

A football field is 100 yards or 300 feet. The parametric equations for a football thrown from (300, 0) back to the origin at speed $\begin{align*}v\end{align*}$  are:
::足球场为100码或300英尺。

播放段落

$$\begin{align*}x &=-t \cdot v \cdot \cos \left(\frac{\pi}{4} \right)+300 \\ y &=\frac{1}{2} \cdot (-32) \cdot t^2 + t \cdot v \cdot sin \left(\frac{\pi}{4} \right)\end{align*}$$
::xtvcos( 4)+300y=12( - 32t2)+tvsin( 4)

播放段落

Substituting the point (0, 0) in for $\begin{align*}(x, y)\end{align*}$  produces a system of two equations with two variables $\begin{align*}v, t\end{align*}$ .
::将点(0,0)替换为(x,y)产生一个由两个变数和两个变数组成的系统。

播放段落

$$\begin{align*}0 &=-t \cdot v \cdot \cos \left(\frac{\pi}{4} \right)+300 \\ 0 &=\frac{1}{2} \cdot (-32) \cdot t^2 + t \cdot v \cdot \sin \left(\frac{\pi}{4} \right)\end{align*}$$
::=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

播放段落

You can solve this system many different ways, including graphing, the quadratic formula, etc. 
::您可以以多种不同的方式解决这个系统, 包括图形绘制、 二次公式等 。

播放段落

$$\begin{align*}t &=\frac{5 \sqrt{3}}{2} \approx 4.3 \text{ seconds} \\ v&=40\sqrt{6} \approx 97.98 \text{ ft/s}\end{align*}$$
::t=5324.3秒v=40697.98英尺/秒

播放段落

In order for someone to throw a football at a  $\begin{align*}45^\circ\end{align*}$  angle all the way across a football field, they would need to throw at about  $\begin{align*}98 \ ft/s,\end{align*}$  which is about 66.8 mph. 
::球员必须投出大约98英尺/秒, 大约是66.8英里。

播放段落

$$\begin{align*}\frac{98 \text{ ft}}{1 \text{ s}} \cdot \frac{3,\!600 \text{ s}}{1 \text{ hr}} \cdot \frac{1 \text{ mile}}{5280 \text{ ft}} \approx \frac{66.8 \text{ miles}}{1 \text{ hr}}\end{align*}$$
::98英尺1秒3,600秒1小时1英里5280英尺66.8英里1英里

播放段落

Example 6
::例6

播放段落

Suppose Danny stands at the point (300, 0) and launches a football at 67 mph at an angle of $\begin{align*}45^\circ\end{align*}$  towards Johnny, who is at the origin. Suppose Johnny also throws a football towards Danny at 60 mph at an angle of  $\begin{align*}50^\circ,\end{align*}$  at the exact same moment. There is a 4 mph breeze in Johnny's favor. Do the balls collide in midair?
::假设丹尼站在点(300,0),在67英里处向原产地的约翰尼发射一支足球,角度为45英寸,向原产地的约翰尼发射一支足球。如果约翰尼也在同一时刻以60英里向丹尼投掷一支足球,角度为50英里。有4英里的微风有利于约翰尼。球在中空相撞吗?

播放段落

Solution:
::解决方案 :

播放段落

Calculate the velocity of each person and of the wind in feet per second:
::计算每个人的速度和每秒的风速:

播放段落

$$\begin{align*}\frac{67 \text{ miles}}{1 \text{ hr}} \cdot \frac{1 \text{ hr}}{3,\!600 \text{ s}} \cdot \frac{5,\!280 \text{ ft}}{1 \text{ mile}} & \approx 98.27 \text{ ft/s} \\ \frac{60 \text{ miles}}{1 \text{ hr}} \cdot \frac{1 \text{ hr}}{3,\!600 \text{ s}} \cdot \frac{5,\!280 \text{ ft}}{1 \text{ mile}}&= 88 \text{ ft/s} \\ \frac{4 \text{ miles}}{1 \text{ hr}} \cdot \frac{1 \text{ hr}}{3,\!600 \text{ s}} \cdot \frac{5,\!280 \text{ ft}}{1 \text{ mile}} & \approx 5.87 \text{ ft/s}\end{align*}$$
::671英里1 小时1 小时3 600 秒5 280 英尺1 英寸98.27英尺/60英里1 小时1 1 小时3 600 秒5 280 英尺1 英里= 88 英尺/秒4 英里1 小时1 小时3 600 秒5 280 英尺1 英寸 *5.87 英尺/秒

播放段落

The location of Danny's ball can be described with the parametric equations below (in radians). Note that the wind simply adds a linear term .
::Danny球的位置可以用下面(以弧度计)的参数方程式来描述。请注意,风只是增加了一个线性词。

播放段落

$$\begin{align*}x_1 &=-t \cdot 98.27 \cdot \cos \left(\frac{\pi}{4}\right)+300 + 5.87 t \\ y_1 &=\frac{1}{2}\cdot (-32) \cdot t^2+t \cdot 98.27 \cdot \sin\left(\frac{\pi}{4}\right)\end{align*}$$
::+300+5.87ty1=12(-322+t98.27sin)

播放段落

The location of Johnny's ball can be described with the following parametric equations (also in radians):
::强尼球的位置可以用下列参数方程(也以弧度表示):

播放段落

$$\begin{align*}x_2 &=t \cdot 88 \cdot \cos \left (\frac{5\pi}{18}\right)+5.87 t \\ y_2 &=\frac{1}{2} \cdot (-32) \cdot t^2+t \cdot 88 \cdot \sin \left(\frac{5\pi}{18}\right)\end{align*}$$
::x2=t88cos( 5- 18) +5. 87ty2= 12. (-32) t2+t88sin( 5- 18)

播放段落

You might observe that the two graphs overlap at about 125 ft, but this is unimportant because they are probably at that location at different times. Plot the distance over time and see how close the footballs actually get in midair.
::你也许可以看到,这两个图表在125英尺左右重叠,但这并不重要,因为它们可能在不同的时间出现在那个位置。绘制一段时间的距离,看看足球在中空的实际距离有多近。

播放段落

$$\begin{align*}x_3 &=t \\ y_3 &=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\end{align*}$$
::x3=ty3(x2- x1)2+(y2-y1)2

播放段落

The TI-83 may run slower than the TI-84 when you do this calculation, depending on how small your  $\begin{align*}T_{step}\end{align*}$ is. The resulting graph is not a parabola, and the calculator cannot find a minimum in the way it can in other circumstances. Still, you can trace and determine that the footballs get 5.36 ft or closer in midair.
::当您进行这个计算时, TI- 83 可能比 TI- 84 慢, 取决于您的 Tstep 有多小。 由此产生的图表不是抛物线, 计算器无法在其它情况下找到最小值 。 但是, 您可以追踪并确定足球在中空得到5. 36 英尺或更接近 。

播放段落

Example 7
::例7

播放段落

Nikki got on a Ferris wheel 10 seconds ago. She started 2 ft off the ground at the lowest point of the wheel, and will make a complete cycle in 4 minutes. The ride reaches a maximum height of 98 ft and spins clockwise. Write parametric equations that model Nikki's position over time. Where will Nikki be 3 minutes from now? 
::Nikki10秒前上了Ferris车轮。 她从地上开始在方向盘的最低点跳下2英尺, 并在4分钟内完成一个完整的循环。 飞行达到最高高度98英尺, 顺时针旋转。 写出模拟Nikki位置的参数方程。 Nikki从现在开始将在哪里 3分钟?

播放段落

Solution:
::解决方案 :

播放段落

Don't let the 10-second difference confuse you. To deal with the time difference, use  $\begin{align*}\left(t + \frac{1}{6}\right)\end{align*}$ instead of  $\begin{align*}t\end{align*}$ in each equation. When $\begin{align*}t=0\end{align*}$ , 10 seconds  $\begin{align*}\left(\frac{1}{6}\right.\end{align*}$ of a minute $\begin{align*}\left.\right)\end{align*}$ have already elapsed.
::不要让10秒的差异混淆你。 要处理时间差, 请使用( t+16) 而不是 t 方程。 当 t=0, 10秒( 16 分钟) 已经过去 。

播放段落

$$\begin{align*}x &= -48 \cdot \sin\left(\frac{\pi}{2}\left(t+\frac{1}{6}\right)\right) \\ y &= -48 \cdot \cos\left(\frac{\pi}{2}\left(t+\frac{1}{6}\right)\right)+50 \end{align*}$$
::x48sin( 2( t+16) y48cos( 2( t+16) +50

播放段落

At $\begin{align*}t=3, x \approx 46.36\end{align*}$ and $\begin{align*}y \approx 37.58\end{align*}$ .
::at t=3,x46.36 and y37.58.

播放段落

Summary
::摘要

播放段落
• A calculator can reference  internal variables like  $\begin{align*}x_1, y_1\end{align*}$  that have already been set in the calculator's memory to form new variables like  $\begin{align*}x_3, y_3\end{align*}$ .
  ::计算器可以引用计算器内存中已经设定的 x1,y1 等内部变量来形成 x3,y3 等新的变量。
播放段落
• The horizontal and vertical components of parametric equations are the $\begin{align*}x =\end{align*}$  and $\begin{align*}y =\end{align*}$  functions respectively.
  ::参数方程的横向和纵向组成部分分别为 x= 和 y= 函数。

播放段落

Review
::回顾

播放段落

Candice gets on a Ferris wheel at its lowest point, 3 feet off the ground. The Ferris wheel spins clockwise to a maximum height of 103 feet, making a complete cycle in 5 minutes.
::坎迪斯在离地面3英尺的最低点乘着摩天轮。摩天轮顺时速旋转到最高高度103英尺,在5分钟内完成整个循环。

播放段落

1. Write a set of parametric equations to model Candice's position.
::1. 编写一套模拟Candice位置的参数方程。

播放段落

2. Where will Candice be in 2 minutes?
::2. 2分钟后Candice会在哪里?

播放段落

3. Where will Candice be in 4 minutes?
::3. 4分钟后Candice会在哪里?

播放段落

One minute ago, Guillermo got on a Ferris wheel at its lowest point, 3 feet off the ground. The Ferris wheel spins clockwise to a maximum height of 83 feet, making a complete cycle in 6 minutes.
::一分钟前,吉列尔莫在离地面3英尺的最低处乘着摩天轮。摩天轮顺时速旋转到最高高度83英尺,6分钟后完成整个循环。

播放段落

4. Write a set of parametric equations to model Guillermo's position.
::4. 编写一套参数方程,以模拟吉列尔莫的位置。

播放段落

5. Where will Guillermo be in 2 minutes?
::5. 两分钟后吉列尔莫会在哪?

播放段落

6. Where will Guillermo be in 4 minutes?
::6. 四分钟后吉列尔莫会在哪?

播放段落

Kim throws a ball from (0, 5) to the right at 50 mph at a  $\begin{align*}45^\circ \end{align*}$ angle.
::金从(0, 5)向右投球, 球在50mph, 角度是45。

播放段落

7. Write a set of parametric equations to model the position of the ball.
::7. 编写一套参数方程,以模拟球的位置。

播放段落

8. Where will the ball be in 2 seconds?
::8. 2秒后球会在哪里?

播放段落

9. How far does the ball get before it lands?
::9. 球落地前有多远?

播放段落

David throws a ball from (0, 7) to the right at 70 mph at a  $\begin{align*}60^\circ \end{align*}$ angle. There is a 6-mph wind in David's favor.
::大卫向右投球,从(0, 7) 向右投球 70 mph , 角度是 60 。 有6 mph 的风有利于大卫 。

播放段落

10. Write a set of parametric equations to model the position of the ball.
::10. 编写一套参数方程,以模拟球的位置。

播放段落

11. Where will the ball be in 2 seconds?
::11. 2秒后球会在哪里?

播放段落

12. How far does the ball get before it lands?
::12. 球落地前有多远?

播放段落

Suppose Riley stands at the point (250, 0) and launches a football at 72 mph at an angle of  $\begin{align*}60^\circ \end{align*}$ towards Kristy who is at the origin. Suppose Kristy also throws a football towards Riley at 65 mph at an angle of  $\begin{align*}45^\circ \end{align*}$ at the exact same moment. There is a 6-mph breeze in Kristy's favor.
::假设Riley站在(250,0)点,在72英里处向原产地的Kristy发射一支橄榄球,角度为60英里。假设Kristy也在65英里处向Riley投掷一支橄榄球,角度为45英里。有6英里的微风有利于Kristy。

播放段落

13. Write a set of parametric equations to model the position of Riley's ball.
::13. 编写一套参数方程,以模拟莱利球的位置。

播放段落

14. Write a set of parametric equations to model the position of Kristy's ball.
::14. 编写一套参数方程,以模拟Kristy球的位置。

播放段落

15. Graph both functions and explain how you know that the footballs don't collide even though the two graphs intersect.
::15. 绘制两个功能的图,并解释你如何知道足球不会相撞,即使两个图形相互交叉。

播放段落

Review  (A nswers )  
::回顾(答复)

播放段落

Please see the Appendix.
::请参看附录。