回答 - 第4章:指数和对数函数
章节大纲
-
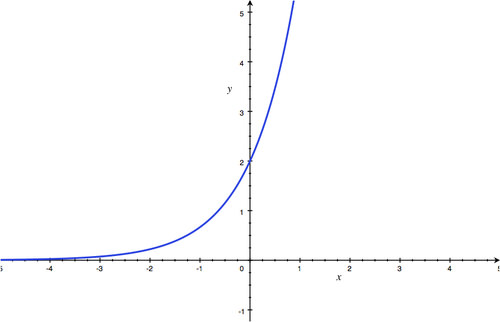
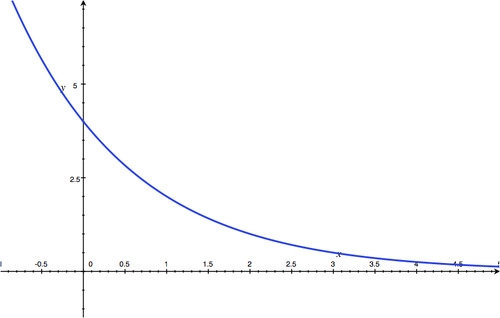
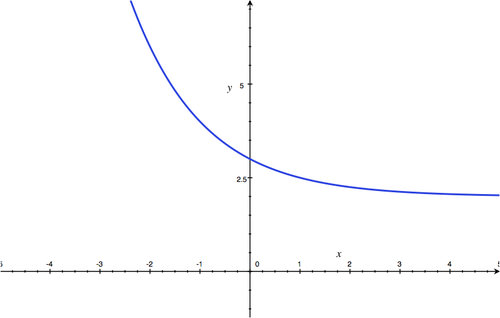
Section 4.2: Graphing and Evaluating Exponential Functions
::第4.2节:绘制图表和评估指数职能-
::y=5=5=5x -
::y=2×4x y=2×4x -
::y=16=3x -
-
-
-
::y=2x y=2x -
::y=2x y=2x -
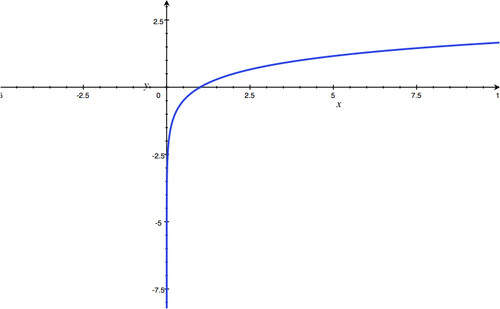
::y=-2x y=-2x -
will be moved to the right 4 spaces.
::f(x) = 3x-4 将移到右边的 4 空格 。
::f(x) = 3x-4 将移到右边的 4 空格 。 -
will be reflected across the axis.
::f(x) =-4x 将反射到 x 轴。
::f(x) =-4x 将反射到 x 轴。 -
will be moved down 2 spaces.
::f(x)=3x-2 将会向下移动两个空格 。
::f(x)=3x-2 将会向下移动两个空格 。 -
will move left 2 spaces, and be reflected over the axis.
::f(x) =-5x+2 将左移两个空格,并反映在 x 轴上方。
::f(x) =-5x+2 将左移两个空格,并反映在 x 轴上方。 -
will be moved down 3 spaces and right 4 spaces.
::f(x) = 5x-4-3 将会向下移动 3 个空格和右 4 个空格 。
::f(x) = 5x-4-3 将会向下移动 3 个空格和右 4 个空格 。 -
Because the -intercept occurs where and → → .
::因为y- interview 发生于 x=0 和 y=a&b0 y=a1 y=a。
::因为y- interview 发生于 x=0 和 y=a&b0 y=a1 y=a。 -
10,485,760 rabbits
::10 485 760只兔子 -
Approximately 1.138 grams
::约1 138克
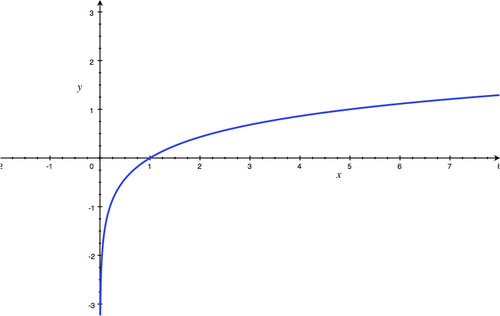
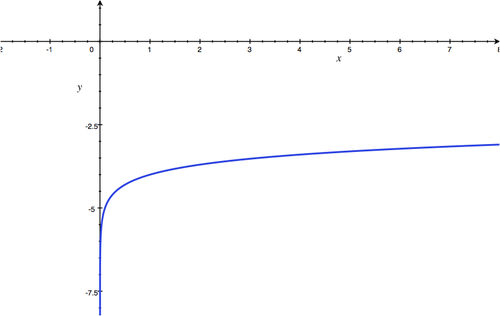
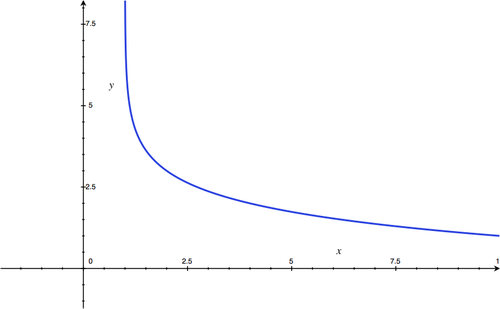
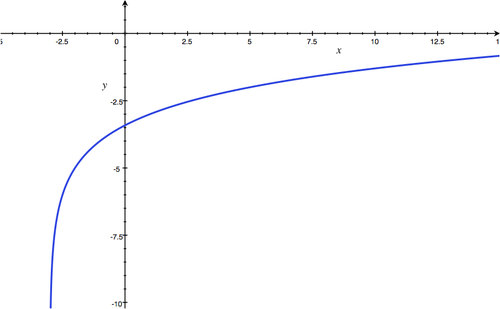
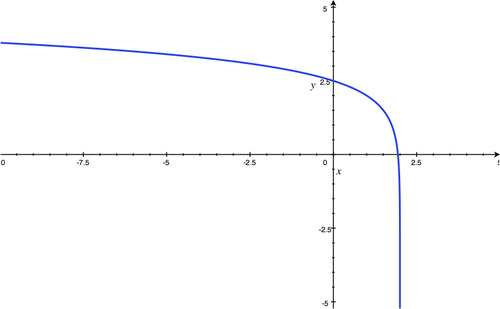
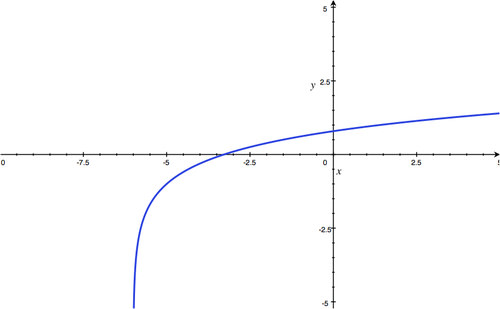
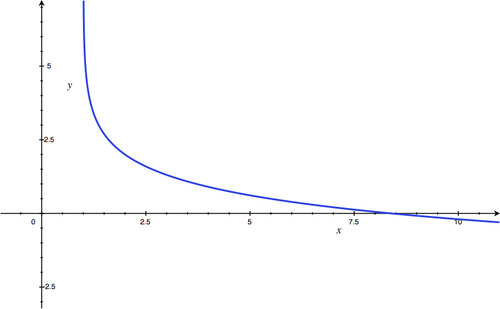
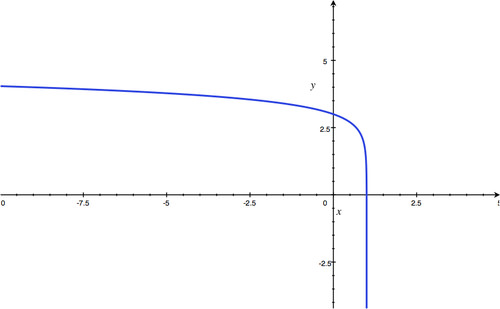
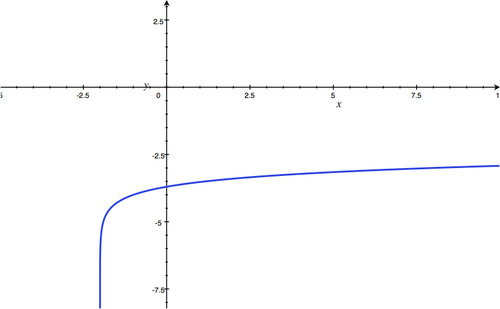
Section 4.3: Graphing and Evaluating Logarithmic Functions
::第4.3节:绘图和评估对数函数-
-
-
-
-
-
-
-
-
-
-
You could graph it as
.
::您可以用对数(x)log(4)来图示它。 -
-
Yes
::是 是 -
No
::否 无 -
No
::否 无
4.4 Properties of Logs
::4.4 日志属性-
False
::假假 -
False
::假假 -
True
::真实 -
::log ( 8x2+16x) -
::对数============================================================================================ -
::log2( 3x4y) -
::对数 3z4 -
::对数 4 @% 2+3log4_x-log4_% 5 -
::In4+lnx+2lny-ln15 -
::2log_x+3log_y+3log_z_log%3 -
::对数 2\\\\\\ 10=x+1 -
::212=x-1 -
Let
. Then
and
. Take the log base b of both sides, and you have
. Simplify to get
. Solve for
and you have
. Since both
and
are equal to
, they are equal to each other.
::Let y=logbnx. 然后 (bn)y=x 和 bny=x. 使用两边的对数基准 b, 您有( ny) logbb=logbx. 简化以获得 ny=logbx. solve y, 您有 y=1nlogbx. 由于 1nlogbx 和 logbnx 都等于 y, 它们彼此相等 。 -
From the previous problem, you know that
Use the exponentiation property, and you have
which simplifies to
.
::从上一个问题中, 您知道对数 {( xn) =1nlogb}}xn。 使用引号属性, 您有 1nlogb}xn =n(1n) logb}x, 它简化为对数 {x 。 -
Let
. Then
. You can rewrite this equation as
You can then rewrite in logarithmic form as
. Since both
and
are equal to
, they are equal to each other.
::y=log1b1x. 让我们y=log1b1x. 然后 (1b)y=1x. 您可以重写此方程式为 x=by。 然后您可以重写对数格式为logbx=y。 由于logbx和log1b1x都等于y, 它们彼此等同 。
Section 4.5: Solving Exponential Equations Using Logs
::第4.5节:使用日志解决指数等同-
::x=1.292x=1.292 -
::x=0.431xx=0.431 -
::x=0.697xx=0.697 -
::x=1.333x=1.333 -
::x=3.754x=3.754 -
::x=0.783x=0.783 -
::x=-2x=2 -
::x=1 x=1 -
::x=3.0259 -
::x8.9872x8.9872 -
::x=log(c+a)logb -
::x=- 0.057 -
::x=1.8x=1.8 -
::x=2x=2 -
::x=27x=27
Section 4.6: Solving Logarithmic Equations
::第4.6节:解决对数等数-
::x=32,768x=32,768 -
::x498.831 -
::x=86x=86 -
::x=170 x=170 -
::x1132 -
::x=33=1.442 -
::x=2x=2 -
::x=1 x=1 -
::x=8x=8 -
::x=27x=27 -
::x=2x=2 -
::x*3.272 -
::x=43 x=43 -
::x=2+211=8.633 -
::x=6x=6
Section 4.7: Compound Interest
::第4.7节:复合利息-
The compound interest formula is
::复合利息公式为 A(t)=p(1+r)t。 -
They would have earned $373.82.
::他们本可以挣373.82美元。 -
Kyle's balance would be $1,098.81.
::Kyle的余额将是1 098.81美元。 -
Yearly simple interest is effectively the same as compound interest compounding yearly. Roberta would have $18,022.10 in the account.
::一年简单利息实际上与每年复利复利相同,罗伯塔账户中有18 022.10美元。 -
The bank has been paying approximately 3.5% annually.
::银行每年支付约3.5%。 -
She could expect to have $3,122.
::她可以指望有3 122美元。 -
There is a balance of $885.08.
::余额为885.08美元。 -
Her original deposit was $650.
::她原先的存款是650美元 -
$7,500
:xx) = 30000(1.14x) 7 500美元
-
He will owe a total of $318.27.
::他将共欠318.27美元。 - $600
- $715.56
- $15,300.14
- $13,138.75
Section 4.8: Population Growth Models and Logistic Functions
::第4.8节:人口增长模式和后勤职能-
::f(x) = 121+1.40. 51x -
::f(x) = 2001+130. 8027x -
::f(x)=1,51+90.749x -
::f(x) = 1 000 0001+90. 959x -
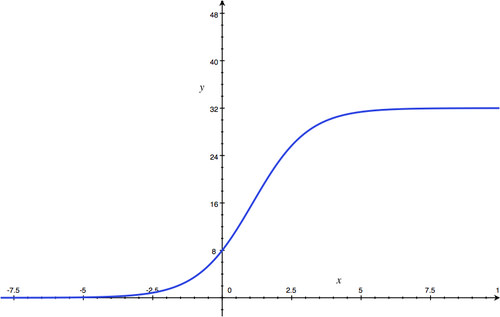
::f(x)=30 000 0001+2.750.89x - 32
- 8
-
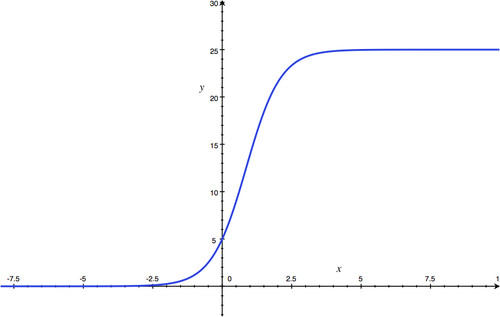
- 25
- 5
-
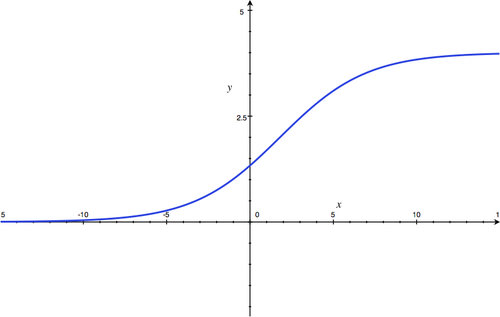
- 4
-
-
Any function in the form
where
.
::窗体 f(x) = c1+ab-x 中的任何函数,其中 0<b> 1。
-