带有决定因素的面积和数量

If we interpret determinants geometrically, we get some really beautiful formulas.
::如果我们对决定因素进行几何解释,我们就会得到一些非常美丽的公式。

First off, given a 2x2 matrix  $\begin{array}{r}det(\left[\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right])\end{array}$  has the property that that determinant is equal to the area of the parallelogram formed by those two vectors. And similarly, in a three by three case we get that the determinant is the volume of the parallelepiped formed by the three column vectors we see in the matrix.
::首先,如果给一个 2x2 矩阵 det ([a1a2b1b2]) , 则该决定因素的属性等于这两个矢量构成的平行图面积。 同样, 在三三三的情况下, 我们得到的决定因素是 由三列矢量构成的平行气管的体积 。

Let's look at an example of this:
::举个例子:

$\begin{array}{r}A=\left[\begin{array}{cc}{x}_1& 0\\ 0& x_2\end{array}\right]\end{array}$
::A=[x100x2]

and the the columns of this form the vectors  $\begin{array}{r}\left[\begin{array}{c}{x}_1\\ 0\end{array}\right],\left[\begin{array}{c}0\\ x_2\end{array}\right]\end{array}$  and looking at this as a rectangle gives us 
::以此形状的列为矢量 [x10] , [0x2] , 并将它作为矩形来看待 。

and the area equals  $\begin{array}{r}{x}_1{x}_2\end{array}$  which equals the determinant of A.
::区域等于x1x2,等于A的决定因素。

Now, let's try and get a new matrix  $\begin{array}{r}A=\left[\begin{array}{cc}{x}_1& x_3\\ x_2& x_4\end{array}\right]\end{array}$  and the determinant becomes  $\begin{array}{r}{x}_1{x}_4-x_2{x}_3\end{array}$  which is the area inside the  parallelogram 
::现在,让我们尝试获得一个新的矩阵 A = [x1x3x2x4] , 决定因素变成 x1x4 - x2x3, 这是平行图中的区域

To prove that the determinant equals the area, we have to find the area of the parallelogram.
::为了证明决定因素与区域相等,我们必须找到平行图的区域。

What is actually interesting is that any matrix can be transformed into a diagonal matrix.
::真正有趣的是,任何矩阵都可以转换成对角矩阵。

We know from geometry that given a matrix with columns of vectors  $\begin{array}{r}\stackrel{\to }{v_1}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right],\stackrel{\to }{v_2}=\left[\begin{array}{c}{x}_3\\ x_4\end{array}\right]\end{array}$ and we know that the area of a parallelogram formed by the vectors of  $\begin{array}{r}\stackrel{\to }{v_1},\stackrel{\to }{v_2}\end{array}$  has the same area, given a scalar c, as the parallelogram formed by the vectors  $\begin{array}{r}\stackrel{\to }{v_1},\stackrel{\to }{v_2}+c\stackrel{\to }{v_1}\end{array}$  so hence we can shift the vectors to make it into a diagonal matrix and write the vector as the product of the lengths of the vectors.
::我们从几何学中得知,给定了一个矢量为 v1[x1x2],v2[x3x4]的矩阵,我们知道,由 v1,v2的矢量构成的平行图区域与由矢量v1,v2cv1组成的平行图区域具有相同的区域,与由矢量v1,v2cv1组成的平行图区域相同,因此我们可以将矢量转换成对等矩阵,并将矢量写成矢量长度的产物。

Let's look at some more examples,
::让我们再举几个例子,

$\begin{array}{r}A=\left[\begin{array}{cc}1& -2\\ 3& 5\end{array}\right]\end{array}$
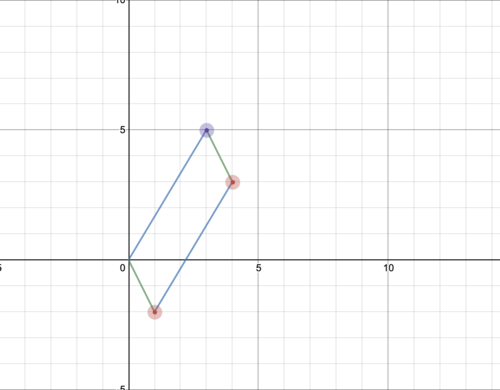
::A=[1-235]

This gives us the vectors
::这给了我们矢量

The area of this is 11 which is also equal to the determinant of the matrix A. 
::这方面有11个领域,也相当于矩阵A的决定因素。