线线函数
章节大纲
-
The Purpose of this Lesson
::本课程的目的In this lesson, you will use a linear function to model a scenario.
::在此教训中,您将使用线性函数来模拟假想。Linear functions are represented using equations, tables, and graphs.
::线性函数使用方程式、表格和图表表示。Introduction: Linear Functions
::导言:线性函数A function is a specific kind of relationship between two quantities. When one of the quantities changes, the other changes also, according to a consistent rule. As the outdoor temperature increases, the number of kids swimming in a pool does too. The further you get from a light source, the dimmer it appears. The more hours you work, the more you earn. Functions can be expressed with equations that demonstrate the relationship between quantities.
::函数是两个数量之间的一种特定关系。当数量变化之一时,其他的也根据一个一致的规则变化。当室外温度上升时,游泳池中的儿童人数也会增加。光源越远,就越显暗。工作的时间越长,挣得越多。函数可以用显示数量之间关系的方程式表示。Y ou'll start by exploring . Linear functions are called linear because their graphs are straight lines.
::首先从探索开始。线性函数被称为线性,因为它们的图形是直线。Linear functions can be used in a zillion ways. Here are just a few:
::线性函数可以以千分之十的方式使用。 这里只有几个:-
Weather forecasting: Linear functions can be used to model temperature patterns over time and predict future weather conditions.
::天气预报:线性函数可用于测算一段时间的温度模式,并预测未来的天气状况。 -
Rocket science: Linear functions can be used to calculate the trajectory of a rocket and predict its landing spot.
::火箭科学:线性函数可用于计算火箭的轨迹并预测其着陆地点。 -
Cryptography: Linear functions can be used to encrypt and decrypt messages, by making them unreadable to anyone without the proper key.
::加密:线性函数可用于加密和解密信件,使没有适当密钥的人无法读取。 -
Genetics: Linear functions can be used to study the inheritance of genetic traits and predict the likelihood of certain diseases or characteristics in offspring.
::遗传学:线性功能可用于研究遗传特征的遗传,并预测后代中某些疾病或特征的可能性。 -
Robotics: Linear functions can be used to control the movement and actions of robots, by describing the position and
speed
of their motors and sensors.
::机器人:线性函数可用于控制机器人的移动和行动,说明其发动机和传感器的位置和速度。
Activity 1: Representing Linear Functions
::活动1:代表线性职能A function is kind of like a magic trick Example 1-1
::例1-1Imagine a sorceress who converts the number of blueberries given to her by multiplying them by 2 then adding 9. After she performs her magic on the 'input' (the number of blueberries she is given), she returns the 'output' (the new number of berries). What expression would represent this process? Below are a few possibilities. Which correctly describe(s) the rule "multiply by 2 , then add 9"?
::想象一下一个女巫,她通过乘以2来转换给她的蓝莓数量,然后加上9。在她施展了“投入”的魔法(她得到的蓝莓数量)之后,她返回了“产出”(新增加的浆果数量),什么表达方式代表这个过程?下面是几种可能性。谁正确描述规则“乘以2,再加9”?9 x + 2 x ( 2 ) + 9 2 x + 9 2 x − 9 2 ( x + 9 )
::9x+2x(2)+92x+92x-92(x+9)Solution: Both x ( 2 ) + 9 and 2 x + 9 above are correct representations of the magic the sorceress performs. The variable x represents the number of blueberries given to the sorceress. Here, x is multiplied by 2 , then 9 is added. A new variable ( y is commonly used) can be used to express the number she returns.
::解析度 : 以上 x(2)+9 和 2x+9 是魔力的正确表达方式 。 变量 x 代表给魔力的蓝莓数量 。 这里, x 乘以 2 乘以 2 , 然后添加 9 。 新的变量( 通常使用 y) 可用于表达她返回的数 。Work it Out
::工作出来The following table is another representation of the sorceress scenario:
::下表是收缩情况的另一个表示:x y 0 9 1 11 2 13 3 15
::xy09111213315-
What do the
y
values represent in
terms
of the scenario? What patterns
can you
see in the table? For every increase of
1
for
x
, how much does
y
increase by? Why?
::假设情景中 Y 值代表什么? 您可以在表格中看到什么模式 ? 对于每增加一个 x, 增加多少? 为什么?
-
Which of the following represent(s) the relationship between
x
and
y
?
Explain.
::下列哪些代表 x 和 y 之间的关系? 请解释 。
2 x = y 2 x = y + 9 x = 2 y + 9 y = 2 x + 9 y − 9 = 2 x
::2x=y2x=y+9x=2y+9y=2x-9y=9x
CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动
Activity 2: Equations and Graphs of Linear Functions
::活动2:线性函数的方形和图示Y ou can think of the spell the sorceress casts as a function. The sorceress performs the magic 'function' on the blueberries she is given. She transforms them according to a mathematical rule, y = 2 x + 9 . This equation tells us how the spell functions - it tells us the magic that the sorceress performs. Note that the "+9" indicates the number of berries she returns when given zero berries to start, since 2(0) = 0. This means that when x is zero, y is 9.
::您可以将女巫施的咒语当作一个函数。 女巫在她得到的蓝莓上执行魔法“ 功能” 。 她根据数学规则, y=2x+9, 将咒语转换为“ 功能 ” 。 这个方程式告诉我们咒语的功能 - 它告诉我们女巫所施的魔法。 请注意, “ +9 ” 表示在给她零浆果时, 她返回的浆果数量, 因为给的果子是 2( 0) = 0。 这意味着当 x 是 0, y 是 9 。 这意味着当 x 是 0 时, y 是 9 。Work it Out
::工作出来-
One of the graphs below is a representation of the equation
y
=
2
x
+
9.
Which one? How do you
know
? (Hint - Remember how many berries the spell returns when she starts with zero?)
::下面的图表之一是 y=2x+9 方程式的表示式。 哪一个? 您怎么知道 ? (Hint - 记得当她以零开头时, 咒语返回多少个浆果 ? )
-
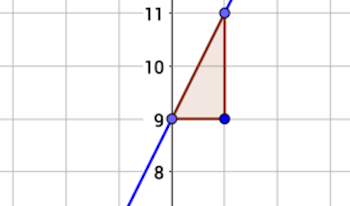
Part of the line described by
y
=
2
x
+
9
is graphed again below, along with a
triangle
. What features of this graph tell you that this is the graph of
y
=
2
x
+
9
?
::Y=2x+9 所描述的线条的一部分与三角形一起在下面再次绘制图解。本图的哪些特点显示这是 y=2x+9 的图解?+
-
Which of the following statements express(es)
the
idea of a slope of 2?
::下列哪些声明表示斜坡为2的想法?
rise run = 2 1 m = 2 Δ y Δ x = 2 1 y 2 − y 1 x 2 − x 1 = 11 − 9 1 − 0 b = 2Slope-intercept Form of a Linear Equation
::线性赤道的斜度截断形式The slope-intercept form of a linear equation is y = m x + b .
::线性方程的斜度截断形式为y=mx+b。-
The
variable
b
identifies the
y
-
intercept
of a line in slope-intercept form
.
The
y
-intercept is the
y
-coordinate of the point where the line crosses the
vertical axis
of the graph.
::变量b 以斜坡截面表示线的 Y 界面。 Y 截面是线穿过图形垂直轴点的Y 坐标。 -
The variable
m
identifies the slope of a line is described as
r
i
s
e
r
u
n
,
or
change in y values
change in x values
.
The slope is a measure of the steepness of a line.
::变量 m 表示线的斜坡, 或以 x 值更改 y 值。 该斜坡是线的斜度的测量值 。
A y -coordinate is equal to the slope multiplied by the corresponding x -coordinate, added to the y -intercept.
::Y座标等于斜度乘以相应的x座标,添加到 Y 界面中。
Interactive
::交互式互动Use the following interactive to explore linear functions and answer the questions that follow.
::使用以下互动方式来探索线性函数并回答以下问题。Summary
::摘要-
Linear functions express a relationship between two changing quantities.
::线性函数表示两个数量变化之间的关系。 -
A function takes
x
values as input and produces corresponding
y
values as output.
::函数将 x 值作为输入,并将相应的y 值作为输出产生。 -
A function relationship can be expressed with tables, equations, and graphs.
::函数关系可以用表格、方程式和图表表示。 -
The graph of a linear function is a line.
::线性函数的图形是线性函数的直线。 -
The slope-intercept form of a line is
y
=
m
x
+
b
,
where
m
is the slope, and
b
is the
y
-intercept.
::一条线的斜度截取形式是 y=mx+b, m 是斜度, b 是 y 截取 。
-
Weather forecasting: Linear functions can be used to model temperature patterns over time and predict future weather conditions.