数量类型

播放段落

In this lesson, you will explore rational and irrational numbers through the Pythagorean Theorem, prove that  $\begin{align*}\sqrt{2}\end{align*}$  is irrational, and learn the identification and characteristics of irrational numbers.
::在这个教训中,你将通过《毕达哥里安理论论》探索理性和非理性数字,证明"%2"是非理性的,并学习非理性数字的识别和特征。

播放段落

Introduction:  Rational and Irrational Numbers
::导言:合理和不合理数字

播放段落

Real  numbers can be graphed on a number line . There are two types of real numbers: rational and irrational. can be written as the ratio of two integers, while irrational numbers cannot.
::真实数字可以用数字行绘制图表。 真实数字有两种类型: 理性和非理性。 可以写成两个整数之比, 而非理性数字则不能 。

播放段落

PLIX Interactive
::PLIX 交互式互动

---

播放段落

Activity 1: Rational and Irrational Numbers in Right Triangles
::活动1:右三角的理性和不合理数字

播放段落

Example 1-1
::例1-1

播放段落

Pythagoras is famous for his theorem relating the three sides of a right triangle. If a triangle is right with legs $\begin{align*}a\end{align*}$  and $\begin{align*}b\end{align*}$  and hypotenuse  $\begin{align*}c\end{align*}$ , then  $\begin{align*}a^2+b^2=c^2\end{align*}$ . Find three integers that make this equation true. Now, double those values. Do the resulting values also make the equation true? Now, divide the original values by 3. Do the resulting values make the equation true? Sketch the resulting right triangles. Are all these values rational? How do you know?
::Pythagoras以其将右三角形的三面联系起来的理论而出名。 如果三角形右对齐, 右腿a和b, 下角c, 那么a2+b2=c2 。 找到三个整数, 使这个方程真实。 现在, 加倍这些数值。 由此得出的数值是否也使方程真实? 现在, 将原始值除以3 。 由此得出的数值是否使方程真实? 将右三角形涂层涂抹出来。 所有这些数值是否都合理? 你怎么知道 ?

播放段落

Solution:  With some guessing you may have stumbled upon one of many  Pythagorean Triples . A Pythagorean Triple is a set of 3 integers that satisfy the Pythagorean Theorem. Here are several Pythagorean Triples:
::解答: 有一些猜想, 你可能偶然发现了许多毕达哥伦三联赛中的一个。 毕达哥伦三联赛是一组3整数, 满足了毕达哥伦理论。 以下是几个毕达哥伦三联赛:

$$\begin{align*}\begin{array}{c} 3,4,5\\ 5,12,13\\ 8,15,17\\ 7,24,25\\ \end{array} \end{align*}$$

播放段落

Any Pythagorean Triple can be selected to complete the exploration, but 3,4,5 can be used for simplicity.
::为完成勘探,可以选择任何Pydagoren三重船,但3,4,5轻便可以使用。

播放段落

Doubling these values gives 6,8,10, which also satisfies the Pythagorean Theorem.
::将这些数值乘以一倍,就提供了6,8,10,这也满足了毕达哥伦神话。

播放段落

Dividing each value by 3 gives  $\begin{align*}1,\frac43, \frac53\end{align*}$ , which also satisfies the Pythagorean Theorem.
::每个数值除以 3 等于 1 4353 , 也满足了毕达哥伦神话。

播放段落

All the values for side lengths used so far are rational because they are each the ratio of two integers.
::迄今为止使用的侧边长度的所有值都是合理的,因为它们都是两个整数之比。

播放段落

Interactive 
::交互式互动

播放段落

Pythagoras was quite keen on right triangles with rational side lengths. He liked to think that the world was so well-ordered that all lengths could be written as a ratio of two integers. Use the interactive below to explore right triangles with rational side lengths. Write down several Pythagorean Triples you find.
::Pytagoras 相当热衷于使用合理侧边长度的右三角形。 他喜欢认为世界秩序井然有序, 所以所有长度都可以以两个整数的比例来刻写。 使用下面的交互作用来用合理的侧长度来探索右三角形 。 写下您找到的几个 Pytagorean Triples 。

播放段落

Example 1-2
::例1-2

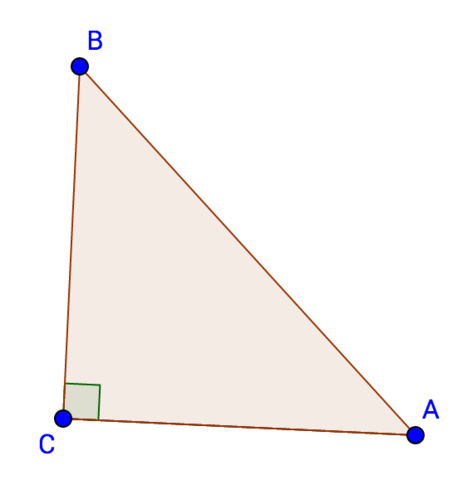
播放段落

Sketch an isosceles right triangle with leg length 1. Use the Pythagorean Theorem to find the length of the hypotenuse. What do you observe?  Is the  result rational or irrational? Why? Sketch three more triangles with integer leg lengths such that the hypotenuse is irrational. 

::将右三角形与腿长1 相拖。 使用 Pythagorean 理论查找下限长度 。 您观察了什么 ? 结果合理还是不合理 ? 为什么? 将另外3个三角形加上整条腿长, 使下限不合理 。

播放段落

Solution:
::解决方案 :

播放段落

Using the Pythagorean Theorem to find the hypotenuse, show that while many  roots  are rational, many are not. Because 2 is not a perfect square, the root of 2 is irrational. If it were rational, there would be a ratio of two integers that you could square to get 2:
::使用 Pytagoren Theorem 来找到低温值, 表明尽管许多根根是理性的, 但很多根不是理性的。 因为 2 不是完美的正方, 2 的根是不理性的。 如果它是理性的, 则有两种整数的比例, 您可以得到 2 :

播放段落

( a b ) 2 = 2

$$\begin{align*}\left(\frac{a}{b}\right)^2=2\end{align*}$$  
:b)2=2

播放段落

It probably seems impossible to find two integers that make the above equation true, and that's because it  is  impossible! Later in this section, you will prove that the root of 2 is irrational
::似乎不可能找到两个整数来使上述方程变为真实, 这是因为不可能。 在此部分稍后部分, 您将会证明 2 的根是非理性的 。

---

播放段落

Activity 2:  Classify Numbers as Rational or Irrational

::活动2:将数字分类为合理或不合理

播放段落

Work it Out
::工作出来

播放段落
1. Various pairs of legs of right triangles are given below. F ind the hypotenuse and state whether the hypotenuse is rational or irrational.
   播放段落
   1. Leg a: 1 unit, Leg b: 2 units
      ::a: 1个单元,b: 2个单元
   播放段落
   2. Leg a:  $\begin{align*}\frac{5}{7} \text{ units,}\end{align*}$  Leg b:  $\begin{align*}\frac{12}{7} \text{ units}\end{align*}$  
      ::a: 57个单元,b: 127个单元
   播放段落
   3. Leg a:  $\begin{align*}\frac{33}{15} \text{ units,}\end{align*}$  Leg b:  $\begin{align*}\frac{44}{15} \text{ units}\end{align*}$  
      ::a:3315个单元,b:4415个单元
   播放段落
   4. Leg a: 16 units, Leg b: 30 units
      ::a:16个单元,b:30个单元
   播放段落
   5. Leg a:  $\begin{align*}\frac{9}{11}\text{ units,}\end{align*}$  Leg b:  $\begin{align*}\frac{40}{11}\text{ units}\end{align*}$  
      ::a:911个单元,b:4011个单元
   播放段落
   6. Leg a: 10 units, Leg b: 10 units
      ::立法:10个单元,立法b:10个单元
   
   ::右三角形的双腿如下: 查找下限, 说明下限是否合理。 立法 a: 1 个单位, 立法 b: 2 个单位 a: 57 个单位, 立法 b: 127 个单位 a: 3315 个单位, 立法 b: 4415 个单位 a: 16 个单位, 立法 b: 30 个单位 a: 911 个单位, 立法 b: 4011 个单位 a: 10 个单位, 立法 b: 10 个单位
播放段落
2. Are each of the following numbers part of the set of rational numbers? How do you know? Convert each to decimals. Given a number in decimal form, how can you identify it as rational or irrational?
   1. 4
   2. $\begin{align*}\frac{1}{3}\end{align*}$  
   3. -11
   4. $\begin{align*}\frac{4}{5}\end{align*}$  
   5. 0
   6. $\begin{align*}\frac{2}{9}\end{align*}$  
   7. $\begin{align*}\frac{3}{11}\end{align*}$  
   8. $\begin{align*}\frac{2}{7}\end{align*}$  
   
   ::下列数字都是理性数字集的一部分吗 ? 你怎么知道? 将每个数字转换为十进制。 如果以十进制出现数字, 如何将其识别为合理或不合理? 4 13 - 11 45 0 29 311 27
播放段落
3. Is  $\begin{align*}\sqrt{10}\end{align*}$  closer to  $\begin{align*}\sqrt{16}\end{align*}$  or  $\begin{align*}\sqrt{9}\end{align*}$ ? Use this fact to quickly but roughly estimate the value of  $\begin{align*}\sqrt{10}.\end{align*}$  Use the same reasoning to quickly approximate the following square roots: 
   1. $\begin{align*}\sqrt{5}\end{align*}$  
   2. $\begin{align*}\sqrt{7}\end{align*}$  
   3. $\begin{align*}\sqrt{12}\end{align*}$  
   4. $\begin{align*}\sqrt{21}\end{align*}$  
   5. $\begin{align*}\sqrt{107}\end{align*}$  
   
   ::?
播放段落
4. Use a calculator to get decimal approximations for each of the roots in the last problem. Round your answer to the number of places shown on your calculator. How do you know these values are approximations and not exact?
   ::使用计算器来为最后一个问题中的根部获得小数点近似值。 将您对计算器上显示的位置数的答案四舍五入。 你怎么知道这些值是近数而不是精确值?
播放段落
5. One way to generate irrational numbers is to take square roots of numbers that aren't perfect squares. Can you think of other ways to generate irrational numbers? Can you think of other irrational numbers besides irrational roots?
   ::产生非理性数字的方法之一是从非完美的平方数字中找出正方根。 你能想出其他方法来产生非理性数字吗? 除了非理性根数之外,你能想到其他非理性数字吗?

播放段落

Interactive
::交互式互动

播放段落

Use the interactive below to examine irrational roots to greater precision. Is it possible for these decimals to terminate or repeat? Why or why not? 
::使用下面的交互效果来更精确地检查非理性根根。 这些小数是否可能终止或重复? 为什么或为什么没有?

播放段落

As you can see, the decimals go on  and on. If you curious to see more decimal places, in 1994, some NASA scientists calculated !
::如你所见,小数点一直持续。如果你想知道更多小数点,1994年,一些美国航天局科学家计算了!

播放段落

Interactive (Extension)
::交互式(扩展)

播放段落

The interactive below computes the ratio of the perimeter of a regular polygon to twice the distance   from  its center to a vertex. Observe how the ratio changes as the number of sides increase. Do you recognize the decimal approximation for this number? Is this number rational or irrational? Is this number a square root of a rational number ? 
::下面的互动计算正则多边形周边与从中心到顶端的距离的两倍之比。 观察边数增加时比率的变化。 您是否识别此数字的小数近似值? 这个数字是否合理? 这个数字是合理数字的平方根吗 ?

播放段落

Proving the Root of 2 is Irrational (Extension)
::证明2之根为不合理(扩展)

播放段落

It seems intuitively clear that the root of 2 is irrational. It is not possible to find  a fraction that can be squared such that the result is 2:
::直觉上似乎很清楚,2的根部是非理性的。 无法找到一个可以平分到结果为 2 的分数 :

播放段落

$$\begin{align*}\left(\frac{a}{b}\right)^2=2\end{align*}$$
:b)2=2

播放段落

So it seems like it must be irrational, but can you prove that it is? The goal is to show that no reduced ratio of two integers satisfies this equation. P roof begins with understanding three ideas:
::因此,它似乎必须是非理性的,但你能证明它是非理性的吗? 目标是显示两个整数的减少比例不能满足这个等式。 证据从理解三个想法开始:

播放段落
1. A reduced ratio of two integers  can't have even numbers in the numerator  and denominator . Why not?
   ::降低两个整数的比例时, 分子和分母的数值是相等的。 为什么不呢 ?
播放段落
2. The square of an odd number is always ___________. (Experiment to answer this question.)
   ::奇数的正方形总是 。 (回答这个问题的经验。 )
播放段落
3. The square of an even number is always a multiple of __________. (Experiment to answer this question.)
   
   The proof that the root of 2 is irrational is a proof by contradiction .  It begins by assuming that the root of 2 is  rational , then proving that this assumption is false because it leads to a contradiction.
   
   $$\begin{align*}\begin{array}{l|l} \left(\frac{a}{b}\right)^2=2 & \small{ \text{Assumed for this proof.}~\frac{a}{b}~\text{is a reduced ratio of 2 integers}}\\ &\small{\text{Therefore} ~a~\text{and}~b~\text{can not both be even.}}\\ \frac{a^2}{b^2}=2 & \small{\text{Property of exponents.}}\\ 2b^2=a^2 & \small{\text{Multiplying by}~2.}\\ a^2=2b^2 & \small{\text{Re-arranging.}}\\ \end{array}\end{align*}$$  
   ::偶数的平方始终是 + 的倍数 。 ( 要回答这个问题的实验 。) 证明 2 的根是非理性的证明是矛盾的证明。 它首先假设 2 的根是理性的, 然后证明这一假设是虚假的, 因为它会导致矛盾 。 (ab) 2= 2 = 2 假定为此证明。 ab 是 降低的 2 整数比率, 因此 a和 b 的比不能两者均匀 。 a2b2b2=2 expents.2b2=a2 Multiping by 2.a2= 2b2 Recranting 。

播放段落

Because  $\begin{align*}a^2\end{align*}$  is 2 times the square of an integer,  $\begin{align*}a^2\end{align*}$  is even.
A square is either odd or a multiple of 4, and since  $\begin{align*}a^2\end{align*}$  is even, it's a multiple of 4, which means  $\begin{align*}a\end{align*}$  is even.
Now,  re-arrange the last equation above by :
::由于 a2 是整数的平方的2倍, a2 是均衡的。 一个正方要么是奇数,要么是4的倍数。 由于a2是偶数,它是一个4的倍数,这意味着一个是均数。 现在, 重新排列上方的最后一个方程 :

播放段落

$$\begin{align*}\frac{a^2}{2}=b^2\end{align*}$$
::a22=b2

播放段落

$\begin{align*}a^2\end{align*}$  is a multiple of 4, so dividing it by 2 gives a result that is still even. So  $\begin{align*}b^2\end{align*}$  is even.
If  $\begin{align*}b^2\end{align*}$  is even, it's a multiple of 4, which means  $\begin{align*}b\end{align*}$  is even.
The proof began with the assumption that  $\begin{align*}\frac{a}{b}\end{align*}$  is a reduced ratio of two integers, and this lead to the conclusion that  $\begin{align*}a\end{align*}$  and  $\begin{align*}b\end{align*}$  are both even, which means  $\begin{align*}\frac{a}{b}\end{align*}$  isn't reduced!
The proof led to a contradiction with the  original assumption, which means the  original assumption was false. 
There is no rational number that can be squared to get 2.
So  $\begin{align*}\sqrt2\end{align*}$  is irrational.
::a2 是 4 的乘数, 因此除以 2 得出的结果仍然相等。 b2 是 even。 如果b2 是 even, 就是 4 的乘数就是 4, 意思是 b 是 even。 证据首先假定 ab 是 两个整数的减少比例, 从而得出 a 和 b 是 均匀的, 这意味着 ab 不减 ! 证据导致与最初的假设相矛盾, 这意味着 最初的假设是 假的。 没有合理数字可以方对 2 。 所以% 2 是非理性的 。

---

播放段落

Activity 3:  Arithmetic with Rational and Irrational Numbers
::活动3:有合理和不合理数字的自理

播放段落

Work it Out
::工作出来

播放段落
1. Perform the indicated arithmetic with rational numbers:
   ::使用合理数字执行显示的算术 :

播放段落

$\begin{align*}\begin{array}{ll} \quad \text{a.} & 3+\frac57\\ \quad \text{b.} & 6.2+\frac89\\ \quad \text{c.} & 7-\frac34\\ \quad \text{d.} & \frac38 \cdot \frac83 -1\\ \quad \text{e.} & \left( \frac{\frac56}{\frac67} \right)\\ \quad \text{f.} & \sqrt{9} \cdot \sqrt{16}\\ \quad \text{g.} & \sqrt{\frac{9}{16}}\cdot \sqrt{\frac{25}{36}}\\ \quad \text{h.} & 1.\overline{3}\cdot7 \end{array}\end{align*}$
::a. 3+57b. 6.2+89c.7-34d.38-83-1e.(5667)f.+9=16g.%916=2536h.1。

播放段落

Did every numerical expression above involve rational numbers? How do you know? Were the results always rational? How do you know?
::上面的每个数字表达式是否都包含合理数字?你怎么知道?结果总是合理吗?你怎么知道?

播放段落
2. If $\begin{align*}\sqrt2\end{align*}$  is irrational, how about  $\begin{align*}5+\sqrt2?\end{align*}$   Make an informal argument by thinking  about the decimal form of $\begin{align*}\sqrt2.\end{align*}$   Make a more rigorous argument related to the proof that  $\begin{align*}\sqrt2\end{align*}$  is irrational.
   ::如果"% 2" 是非理性的, 那么5"% 2" 如何? 思考小数点的"% 2" 的形式来做一个非正式的争论。 做一个更严谨的争论, 证明"% 2" 是非理性的。
播放段落
3. Similarly, consider  $\begin{align*}10\sqrt2.\end{align*}$
   ::同样,考虑102。
播放段落
4. Find two irrational numbers whose sum is rational.
   ::找出两个非理性数字 其数额是理性的
播放段落
5. Find two irrational numbers whose product is rational.
   ::找到两个非理性数字 其产品是理性的。
播放段落
6. Perform the indicated arithmetic:
   ::执行指定的算术 :

播放段落

$\begin{align*}\begin{array}{ll} \quad \text{a.} & 5+7+\sqrt2\\ \quad \text{b.} & 6-\sqrt3+8\\ \quad \text{c.} & (4-11)\sqrt5\\ \quad \text{d.} & 4\sqrt5-11\sqrt5\\ \quad \text{e.} & \sqrt4-\sqrt9\\ \quad \text{f.} & \sqrt4-\sqrt10\\ \quad \text{g.} & \sqrt9\cdot\sqrt{25}\\ \quad \text{h.} & \sqrt9\cdot\sqrt2\\ \quad \text{i.} & 3\left(4+\sqrt7\right)\\ \quad \text{j.} & -\sqrt{11}+\sqrt{11}\\ \quad \text{k.} & \sqrt{11}-\sqrt{11}\\ \quad \text{l.} & 2\sqrt{11}-2\sqrt{11}\\ \quad \text{m.} & 3\sqrt{11}-2\sqrt{11}\\ \quad \text{n.} & \left(\frac{\sqrt3}{\sqrt3}\right)\\ \quad \text{o.} & \sqrt{14}\cdot\sqrt{14}\\ \quad \end{array}\end{align*}$
::======================================================================================================================= =====================================================================================================================================================================================================================================================================================================================================================================================================

播放段落
7. Are irrational numbers closed under addition? How about division? What conclusions can you draw about irrational numbers from the exercises above? 
   ::非理性数字是否被加起来了?关于分裂呢?你能从上述练习中得出什么关于非理性数字的结论?