角度 - 定义、类型、互动和实例

播放段落

Line Segment and Ray
::线线段和雷线

播放段落

A line segment   is a portion of a line with two endpoints . A ray   is a portion of a line with one endpoint . Line segments are named by their endpoints and rays are named by their endpoint and another point . In each case, a segment or ray symbol is written above the points. Below, the line segment is   $\begin{align*}\overline{AB}\end{align*}$   and the ray is   $\begin{align*}\overrightarrow{AB}\end{align*}$ .
::线段是两个端点的直线的一部分。 光线是一条端点的直线的一部分。 线段按其端点命名, 光线则按其端点和另一点命名。 在每种情况下, 线段或射线符号都写在这些点之上。 下面, 线段是AB , 光线是AB 。

---

播放段落

What is an Angle?
::什么是角?

播放段落
• When two rays meet at their endpoints, they form an angle .
  ::当两条射线在终点相遇时,它们形成一个角度。
播放段落
• Depending on the situation, an angle can be named with an angle symbol  $\begin{align*}\angle\end{align*}$  and its vertex , or by three letters.
  ::视情况而定,一个角度可以用角度符号及其顶点命名,或用三个字母命名。

播放段落

If three letters are used, the middle letter is the vertex . The angle below could be called   $\begin{align*}\angle B\end{align*}$   or   $\begin{align*}\angle ABC\end{align*}$   or   $\begin{align*}\angle CBA\end{align*}$ . Use three letters to name an angle if using one letter does not clearly indicate what angle you are identifying.
::如果使用三个字母, 中字母就是顶点。 下面的角可以称为 B 或 ABC 或 CBA 。 如果使用一个字母时没有明确说明您所指定的角, 则使用三个字母来命名一个角度 。

播放段落

The size of an angle is measured in degrees. For example, "the measure of the angle $\begin{align*}ABC\end{align*}$ " is often written as $\begin{align*}m \angle ABC\end{align*}$ . You can use a protractor or geometry software to measure angles. Remember that a full circle includes 360 degrees .
::角度的大小以度计。 例如, “ 角度 ABC 的度量” 通常写为 mABC 。 您可以使用一个分数或几何软件来测量角度。 记住一个整圆包括 360 度 。

---

播放段落

Types of Angles
::角度类型

播放段落
• An angle that is exactly $\begin{align*}0^\circ\end{align*}$ is called a zero angle .
  ::一个完全为 0 的角叫做零角度 。
播放段落
• An angle that is less than $\begin{align*}90^\circ\end{align*}$ is called an acute angle .
  ::角小于90的角称为急性角。
播放段落
• An angle that is exactly   $\begin{align*}90^\circ\end{align*}$ (one-quarter of a circle) is called a right angle . A right angle is noted with a small square at its vertex.
  ::角度为 90 ( 圆的四分之一) , 称为 右角 。 右角 在其顶部用小方形标出 。
播放段落
• An angle that is more than   $\begin{align*}90^\circ\end{align*}$ but less than   $\begin{align*}180^\circ\end{align*}$ is called an obtuse angle . An angle that is exactly   $\begin{align*}180^\circ\end{align*}$ (one-half of a circle) is called a straight angle . 
  ::角度大于 90 , 但小于 180 , 叫做 斜角 。 角度恰好是 180 ( 半圆半圈) , 叫做 直角 。

---

播放段落

Identifying the Types of Angles
::识别角的类型

播放段落

Name the angle below and classify it by its measure .
::列出下方角,并按其大小进行分类。

播放段落

$\begin{align*}\angle{F}\end{align*}$ (also written as  $\begin{align*}\angle{DFE}\end{align*}$ or $\begin{align*}\angle{EFD}\end{align*}$ ), is angle.   
::F(亦以DFEOREFD写成)是角度。

播放段落

CK-12 Interactive: Angles and Lines
::CK-12 交互式: 角度和线

---

播放段落

 CK-12 PLIX Interactive: Angles in the Game of Pool
::CK-12 PLIX 互动: 池游戏中的角

---

播放段落

Complementary Angles and Supplementary Angles
::补充角和补充角

播放段落

Two angles are complementary   if the sum of their measures is   $\begin{align*}90^\circ\end{align*}$ .
::如果其措施的总和是90,则两个角度是互补的。

播放段落

Two angles are supplementary   if the sum of their measures is  $\begin{align*}180^\circ\end{align*}$ .
::如果其措施的总和为180,则两个角度是补充性的。

播放段落

Two angles that together form a straight angle will always be supplementary.
::构成直角的两个角度将永远是补充的。

---

播放段落

Finding an Unknown Angle
::查找未知的角

播放段落

$\begin{align*}x\end{align*}$  and  $\begin{align*}y\end{align*}$  are complementary angles with a measure of $\begin{align*}y=20^\circ\end{align*}$ . What is the measure of  $\begin{align*}x\end{align*}$ ?
::x 和 y 是测量 y=20 的互补角度。x 的度量是多少?

播放段落

The measure of  $\begin{align*}x\end{align*}$  is .  
::x 的度量为 。

---

播放段落

Adjacent Angles and Vertical Angles
::相邻角和垂直角

播放段落

When two lines intersect, a variety of angles are formed, as shown below.
::当两条线相交时,形成各种角度,如下文所示。

播放段落

$\begin{align*}\angle AEC\end{align*}$   and   $\begin{align*}\angle AED\end{align*}$   are adjacent angles   because they are next to each other and share a ray. They are also supplementary angles,   because together they form a straight angle.   $\begin{align*}\angle AEC\end{align*}$   and   $\begin{align*}\angle DEB\end{align*}$   are called . Vertical angles   will always have the same measure .
::QAEC 和 QAAED 是相邻角度, 因为它们彼此相邻并共享一个射线。 它们也是补充角度, 因为它们共同形成一个直角 。 QAEC 和 QAEDB 被称为 。 垂直角度将始终具有相同的量度 。

播放段落

Consider this example problem:
::考虑一下这个例子问题:

播放段落

Let  $\begin{align*}m \angle{AEC}=x^\circ\end{align*}$ . Show that  $\begin{align*}m \angle{DEB}\end{align*}$  must also equal  $\begin{align*}x^\circ\end{align*}$ .
::让 mAEC=x。 显示 mDEB 也必须等于 x。

播放段落

This shows that vertical angles will always have the same measure.
::这表明垂直角度将总是具有相同的量度。

---

播放段落

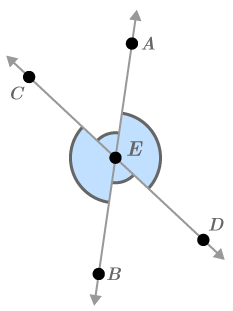
Identifying Angles
::识别角度

播放段落

Explain why you must use three letters to identify any of the angles in the diagram below.
::解释为什么您必须使用三个字母来识别下图中的任何角度。

播放段落

All angles in this diagram have a vertex of  $\begin{align*}E\end{align*}$ . Therefore $\begin{align*}\angle{E}\end{align*}$ is ambiguous because it could refer to many different angles. Use three letters with  $\begin{align*}E\end{align*}$ as the middle letter to be clear about which angle you are identifying $\begin{align*}\angle{AEC}\end{align*}$ , $\begin{align*}\angle{AED}\end{align*}$ , $\begin{align*}\angle{DEB}\end{align*}$ , $\begin{align*}\angle{BEC}\end{align*}$ .       
::此图表中的所有角度都有 E 的顶点 。 因此 E 是模糊的, 因为它可以指许多不同的角度 。 使用三个字母以 E 作为中间字母, 以清楚您正在识别哪个角度 : @ ACE, QAED, QDEB, QBEC 。

---

播放段落

Angles - Examples
::角度 - 示例

播放段落

Example 1
::例1

播放段落

Angles are formed by intersecting lines or rays. If you take any two lines or rays, will you form at least one angle?
::角度由交叉线或射线组成。如果使用任何两条线或射线,您将至少组成一个角度吗?

播放段落

As long as the lines or rays intersect , at least one angle will be formed. If the lines (or rays) are parallel  and therefore don't intersect, then no angles will be formed.
::只要线条或射线交叉,至少将形成一个角度。如果线条(或射线)是平行的,因此不交叉,则不会形成任何角度。

  播放段落

Example 2
::例2

播放段落

Estimate the measure of angle  $\begin{align*}\angle{DFE}\end{align*}$ . Use a protractor to confirm your answer. 
::估计角的度量 DFE。使用减号来确认您的答复 。

播放段落

Remember that exactly half of a right angle is  $\begin{align*}45^\circ\!.\end{align*}$  This angle looks to be more than half of a right angle. You might guess that it is approximately  $\begin{align*}55^\circ\!.\end{align*}$  Using a protractor , you can see that it is about  $\begin{align*}60^\circ\!.\end{align*}$
::记住, 右角的准确一半是 45\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\可以\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

Example 3
::例3

播放段落

What are two lines that form a right angle called?
::构成正确角度的两条线叫什么来着?

播放段落

Perpendicular lines .
::直肠直线

---

播放段落

CK-12 PLIX Interactive: Lines
::CK-12 PLIX 互动:线条

Summary

播放段落 A line segment is a portion of a line with two endpoints. ::直线段是有两端点的直线的一部分。 播放段落 A ray is a portion of a line with one endpoint.  ::A射线是一条线的一部分,端点只有一个。 播放段落 An angle is formed when two rays meet. ::两射线相遇时形成角。 播放段落 A zero angle has 0°. ::零角为0度。 播放段落 An acute angle has less than 90°. ::急性角小于90度。 播放段落 A right angle has exactly 90°. ::右角有90度 播放段落 An obtuse angle is between 90° and 180°. ::斜角在90度至180度之间。 播放段落 A straight angle has exactly 180°. ::直角有180度 播放段落 Complementary angles add up to 90°. ::补充角度加起来可达90度。 播放段落 Supplementary angles add up to 180°. ::补充角度加起来等于180°。

---

播放段落

Review
::审查审查审查审查

播放段落

1. What's the difference between a line segment, a line, and a ray?
::1. 线条、线条和射线之间有什么区别?

播放段落

2. Draw an example of a right angle.
::2. 绘制一个正确角度的例子。

播放段落

3. Draw an example of an obtuse angle.
::3. 举一个隐蔽角度的例子。

播放段落

4. Draw an example of an acute angle.
::4. 绘制一个急性角的例子。

播放段落

5. Why are two angles that make a straight angle always supplementary?
::5. 为什么两个角度使一个直角总是相辅相成的呢?

播放段落

6. If   $\begin{align*}m\angle ABC=(2x+4)^\circ\end{align*}$ ,   $\begin{align*}m\angle DEF=(3x-5)^\circ\end{align*}$ , and   $\begin{align*}\angle ABC\end{align*}$   and   $\begin{align*}\angle DEF\end{align*}$   are complementary, what are the measures of the angles?
::6. 如果 mABC=( 2x+4) , mDEF=( 3x- 5) , 和 ABC 和 DEF 是互补的,那么如何测量角度?

播放段落

7. If   $\begin{align*}m\angle ABC=(2x+4)^\circ\end{align*}$ ,   $\begin{align*}m\angle DEF=(3x-5)^\circ\end{align*}$ , and   $\begin{align*}\angle ABC\end{align*}$   and   $\begin{align*}\angle DEF\end{align*}$   are supplementary, what are the measures of the angles?
::7. 如果 mABC=( 2x+4) , mDEF=( 3x- 5) , 和 ABC 和 DEF 是补充性的,那么角度的量度是多少?

播放段落

Use the diagram below for #8-#12.
::使用下图显示 # 8 - # 12 。

播放段落

8. Identify an example of vertical angles.
::8. 找出垂直角度的例子。

播放段落

9. Identify an example of a straight angle.
::9. 确定一个直角的例子。

播放段落

10. Identify an example of supplementary angles.
::10. 找出一个补充角度的例子。

播放段落

11. If   $\begin{align*}m\angle ABC=70^\circ\end{align*}$ , find   $\begin{align*}m\angle ABF\end{align*}$ .
::11. 如果ABC=70,请找到MABF。

播放段落

12. If   $\begin{align*}m\angle ABC=70^\circ\end{align*}$ , find   $\begin{align*}m\angle FBG\end{align*}$ .
::12. 如果MABC=70,请找到MFBG。

播放段落

13. What do you remember about perpendicular lines?
::13. 你对垂直直线还记得什么?

播放段落

Use the angle   in the image  for #14-#15. 
::使用图像中的 14 - # 15 角度 。

播放段落

14. Identify the angle and classify it based on its size.
::14. 查明角,并根据角的大小进行分类。

播放段落

15. Estimate the measure of the angle. Use a   protractor to confirm your answer.
::15. 估计角度的度量,使用减号确认你的答复。

播放段落

16. Draw a diagram in which two angles are supplementary to the same angle. What must be true about the original two angles? Explain.
::16. 绘制一个图表,其中两个角度是同一角度的补充,原始两个角度必须具备什么真实性?解释。

播放段落

17. We use the term  complementary  to describe angles that sum to ___ and   supplementary   to describe angles that sum to ___.  What about angles that sum to  $\begin{align*}360^\circ\end{align*}$ ? Invent a name for such angles and justify your choice. 
::17. 我们用补充一词来描述总和到...的角,并用补充词来描述总和到...的角。 总计到360的角如何? 为这些角发明一个名称,并证明你选择的理由。

播放段落

18. Draw two vertical angles. How much must each ray of one of the vertical angles be rotated in order to match up with the other vertical angle? Explain.
::18. 绘制两个垂直角度:一个垂直角度的每个射线必须旋转多少才能与其他垂直角度相匹配?解释。

播放段落

19. Draw two angles of the same measure that are not vertical. Draw two angles that are supplementary but not adjacent. Draw two angles that are adjacent and have the same measure.
::19. 绘制不垂直的同一度量的两个角度; 绘制两个补充但不相邻的角; 绘制两个相邻且具有相同度量的角。

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。