四边形 - 定义、类型、属性、互动和实例
Section outline
-
What is a Quadrilateral?
::什么是四方?The prefix "quad-" means "four", and "lateral" is derived from the Latin word for "side". So a quadrilateral is a four-sided polygon . Since it is a polygon, you know that it is a two-dimensional figure made up of straight sides. A quadrilateral also has four angles formed by its four sides.
::“ 夸德” 前缀是指“ 四” , “ 单方面” 则来自拉丁语中的“ 侧边” 。 因此四边是四面多边形。 由于它是多边形, 您知道它是由直面组成的二维数字。 四边也有四个角度由四面组成 。, , and are the sides and , , and are the vertices of the quadrilaterals.
::AB、BC、CD和DA是两边的,A、B、C和D是四边的顶点。Line segments and joining two non-consecutive vertices are called diagonals .
::线段AC和BD连接两个非连续的脊椎,称为对角。Two sides like and having a common endpoint are called adjacent sides.
::诸如AB和AD等具有共同终点的两边被称为相邻的两边。
Types of Quadrilaterals
::四方类型Certain quadrilaterals have special features. Below we review their definitions and properties
::某些四边形具有特殊的特点。 下面我们审查它们的定义和特性。Kite and its Properties
::Kite 及其属性A kite is a convex quadrilateral with two pairs of adjacent congruent , or equal, sides such that not all sides are congruent.
::风筝是一个共和的四边形,有两对相邻的相近相近或相等的两面,因此并非所有两边都是相近的。The angles between the congruent sides are called vertex angles . The other angles are called non-vertex angles .
::相近面之间的角度被称为顶端角度。其他角度则被称为非顶端角度。The Properties of a :
::a 的属性:1. Two pairs of adjacent sides are congruent, i.e., and .
::1. 两对相邻的两边是相同的,即AB=AD和BC=CD。2. Non- vertex angles are congruent, i.e., .
::2. 非垂直角度是相同的,即:ABC-ADC。3. Diagonals intersect each other at right angles, i.e., .
::3. 对角在右角相互交织,即“AOBBOCCODDOA=90”。4. The longer diagonal of a kite bisects the shorter one, i.e., . ("Bisect" means the longer line cuts the shorter one into two equal parts.)
::4. 风筝的对角线越长,其对角线就越短,即BO=OD。 (“Bicome”意指长线将短线一切成两等。 )5. The diagonal through the vertex angles is the angle bisector for both angles, i.e., and .
::5. 通过顶端角的对角线是两个角度,即BACDAC和BCADCA的角线。6. One of the diagonals bisects the kite, i.e., divides it into two , i.e., .
::6. 其中一个对角线将风筝分成两部分,即分为两部分,即ZABCADC。
Trapezoid and its Properties
::草类及其属性A trapezoid is a quadrilateral with exactly one pair of parallel sides. Note: Some texts leave out the word "exactly," which means quadrilaterals with two pairs of parallel sides are sometimes considered . In this course, assume trapezoids have exactly one pair of parallel sides.
::陷阱类动物是一个四边形, 具有一对齐的平行面。 注意: 有些文本忽略了“ 精确的” 一词, 这意味着有两对平行面的四边形有时会被考虑。 在此过程中, 假设陷阱类动物有一对齐的平行面 。The Properties of a Trapezoid :
::轨迹的属性 :1. One pair of opposite sides are parallel, i.e., . (|| is the symbol for parallel lines.)
::1. 一对对对对是平行的,即ABCD。 (是平行线的符号。 )2. The two pairs of adjacent angles along the sides are supplementary, i.e., and .
::2. 沿两侧的两对相邻角是补充性的,即:ABC+BCD=180和QCDAQDAB=180。
Isosceles Trapezoid and its Properties
::Isosceles 轨迹及其属性An isosceles trapezoid is a trapezoid with the non-parallel sides congruent. An additional property of isosceles trapezoids is base angles are congruent.
::等离子细胞类是非平行两面相似的类固膜类固膜。另外,等离子细胞类固膜的特性是基角是同质的。The Properties of an Isosceles Trapezoid :
::Isosceles 轨迹的属性 :1. One pair of opposite sides are parallel, i.e., .
::1. 一对对对对是平行的,即ABCD。2. Two pairs of adjacent angles are supplementary, i.e., and .
::2. 两对相邻角度是补充的,即:ABCBCD=180和CDADAB=180。3. Base angles are congruent, i.e., and .
::3. 基角度是相同的,即:ABC-DAB和BCD-CDA。4. The diagonals are congruent, i.e., .
::4. 对角线是相同的,即AC=BD。
Parallelogram and its Properties
::平行图及其属性A parallelogram is a quadrilateral with two pairs of parallel sides.
::平行图是四边形,两对平行面。The Properties of a :
::a 的属性:1. Opposite sides are parallel, i.e., and .
::1. 对面两面是平行的,即ABCD和BCDA。2. Opposite sides are congruent, i.e., and .
::2. 对面两边是相同的,即AB=CD和BC=DA。3. Opposite angles are congruent, i.e., and .
::3. 对面角度是相同的,即:ABCCDA和DABBCD。4. Adjacent angles are supplementary, i.e., , , and .
::4. 近邻角度是补充性的,即:ABCBCD=180,BCDCDA=180,CDDAB=180和DABABC=180。5. Diagonals bisect each other, i.e., and .
::5. 对角线相互交织,即BO=OD和AO=OC。6. Each diagonal bisects the parallelogram, i.e., divides it into two congruent triangles and .
::6. 每一对角线的两面将平行图分解,即将其分为两个相似的三角形:ZaABCADC和QBCDBAD。
Rectangle and its Properties
::矩形及其属性A rectangle is a quadrilateral with four right angles . All are parallelograms.
::矩形是一个四边形,有四个右角度。全部是平行图。The Properties of a Rectangle :
::矩形的属性 :1. Opposite sides are parallel, i.e., and .
::1. 对面两面是平行的,即ABCD和BCDA。2. Opposite sides are congruent, i.e., and .
::2. 对面两边是相同的,即AB=CD和BC=DA。3. All four of the angles are congruent and measure , i.e., .
::3. 所有四个角度都是相近的,测量90°C,即ABCBCDCDDAB=90°C。4. Diagonals are congruent, i.e., .
::4. 对角是相同的,即AC=BD。5. Diagonals bisect each other, i.e., and .
::5. 对角线相互交织,即BO=OD和AO=OC。
Rhombus and its Properties
::Rhombus 及其属性A rhombus is a quadrilateral with four congruent sides . All rhombuses (or rhombi) are parallelograms.
::圆柱形是四面形的四边形,四面形均匀,所有复方形(或rhombi)都是平行图。The Properties of a Rhombus :
::Rhombus 的属性 :1. Opposite sides are parallel, i.e., and .
::1. 对面两面是平行的,即ABCD和BCDA。2. All four sides are congruent, i.e., .
::2. 所有四个方面都是一致的,即AB=BC=CD=DA。3. Opposite angles are congruent, i.e., and .
::3. 对面角度是相同的,即:ABCCDA和DABBCD。4. Diagonals are the interior angle bisectors, i.e., , , and .
::4. 对角是内角的分区,即:BACDAC、ZBDCBDA、DBCDBA和ZBCDCA。5. Diagonals intersect each other at right angles, i.e., .
::5. 对角在右角相互交织,即“AOBBOCCODDOA=90”。
Square and its Properties
::平方及其属性A square is a quadrilateral with four right angles and four congruent sides . All squares are rectangles and rhombuses.
::方形是一个四边形,有四个右角和四个相近的边。所有方形都是矩形和角形。The Properties of a Square :
::广场的属性 :1. All four sides are congruent, i.e., .
::1. 所有四个方面都是一致的,即AB=BC=CD=DA。2. All the four angles are congruent and measures , i.e., .
::2. 所有四个角度都是一致的,衡量尺度为90,即:aABC+BCD+CDQAQDAB=90。3. Diagonals are congruent, i.e., .
::3. 对角是相同的,即AC=BD。4. Diagonals bisect each other at right angles, i.e., .
::4. 对角在右角度,即“AOBBOC”和“CODDOA=90”上相互交织。
If All the angles of a quadrilateral are congruent and make right angles , what type of quadrilateral is this?
::如果四边形的所有角度都吻合 并形成正确的角度 那么这是哪种四边形?All the angles of a
::一个角度的所有角度都是相近的, 并创造出正确的角度 。
Hierarchy of Quadrilaterals
::四方等级制度Notice that the properties of quadrilaterals overlap . A square is not only a square, but also a rhombus, a rectangle, a parallelogram, and a quadrilateral.
::注意四边形的属性重叠。 方形不仅是一个正方形, 而且还是一个正方形、 矩形、 平行图和四边形 。The following diagram shows the hierarchy of quadrilaterals.
::下图显示了四边形的等级。
CK-12 Interactive PLIX: Parallelogram Classification
::CK-12 交互式PLIX:平行线形分类CK-12 Interactive: Parallelogram Classification
::CK-12 互动:平行线形分类
Exploring Quadrilaterals
::探索四方Click the small blue arrow next to the image below and observe the different quadrilaterals. Explore the angles and lengths by dragging any of the vertices of the quadrilateral.
::单击下方图像旁边的小蓝箭头,观察不同的四边形。通过拖曳四边形的任何顶点来探索角度和长度。Rhombus
::滚轮
Solving for Unknown Values of a Quadrilateral
::解决四边框未知值Solve for (picture not drawn to scale).
::x 的溶解( 图像不绘制为缩放) 。This quadrilateral is marked as having four congruent sides , so it is a rhombus. Rhombuses have the same properties as parallelograms. One property of parallelograms is that opposite angles are congruent . This means that the marked angles in this rhombus must be congruent.
::此四边形标记为四个相容面, 所以它是一个正方形。 伦布斯与平行图具有相同的属性。 平行图的一个属性是相反角度是相容的。 这意味着此正方形的标记角度必须是相容的 。
::x+7=2xx=7
Quadrilaterals - Examples
::四方 - 示例Example 1
::例1All squares are rectangles, but not all rectangles are squares. How is this possible?
::所有方形都是矩形,但并非所有矩形都是方形。这怎么可能?Rectangles are defined as quadrilaterals with four right angles. Squares are defined as quadrilaterals with four right angles and four congruent sides. Because all squares have four right angles and satisfy the definition for rectangles, they can all also be called rectangles. On the other hand, not all rectangles have four congruent sides, so not all rectangles can also be called squares.
::矩形被定义为四个右角度的四边形。 方形被定义为四边形, 四个右角度和四个正方形。 由于所有方形都有四个右角度, 并且符合矩形的定义, 它们也可以被称为矩形。 另一方面, 并非所有矩形都有四个正方形, 所以并非所有矩形都可以被称为正方形 。Example 2
::例2Draw a square. Draw in the diagonals of the square. Make at least one conjecture about the diagonals of the square.
::绘制一个正方形。在正方形的对角线中绘制。至少对正方形的对角线做一个猜想。To make a conjecture means to make an educated guess. There are a few conjectures you might make about the diagonals of a square. In other lessons, you will learn how these conjectures may be proven true.
::假想可以做一个明智的猜测。 对于一个广场的对角, 你可能会做几个猜想。 在其他的教训中, 你会学到这些猜想是如何被证实的。Here are some possible conjectures:
::以下是一些可能的推测:1. diagonals of a square are congruent
::1. 方形的对角线是一致的2. diagonals of a square are perpendicular
::2. 方形的对角是垂直的3. diagonals of a square bisect each other (cut each other in half)
::3. 平方对角对角对角对角(将对角对角对角对角对角对角对角对角对角对角对角对角对角对角对角对角的对角对角对角对角对角对角对角4. diagonals of a square bisect the angles (cut the angles in half)
::4. 方形两角对角的对角(将90角切成两半)Example 3
::例3A quadrilateral has four congruent sides. What type of quadrilateral must it be? What type of quadrilateral could it be?
::一个四边形有四个相似的面。 它必须是什么类型的四边形? 它能是什么类型的四边形?It must be a rhombus and therefore also a parallelogram.
::它必须是一个暴风雨,因此也是一个平行图象。Example 4
::例4Solve for (picture not drawn to scale).
::x 的溶解( 图像不绘制为缩放) 。This is a parallelogram so opposite sides are congruent .
::这是一个平行的图像,所以对立的两面是相同的。
::3x+1=5x-122x=13x=6.5
CK-12 PLIX: Quadrilateral Classification
::CK-12 PLIX: 四方分类Summary -
A
kite
is a convex quadrilateral with two pairs of adjacent congruent sides such that not all sides are congruent.
::风筝是一个共和的四边形,有两对相邻的相近相近面,因此并非所有两边都是一致的。 -
A
trapezoid
is a quadrilateral with exactly one pair of parallel sides.
::甲状腺类是一种四边形, 有着一对齐的平行面。 -
An
isosceles trapezoid
is a trapezoid with the non-parallel sides congruent and the base angles are congruent.
::等离子细胞类动物是非平行面的锥形动物,基角是相同的。 -
A
parallelogram
is a quadrilateral with two pairs of parallel sides.
::平行图是四边形,两对平行面。 -
A
rectangle
is a quadrilateral with four right angles.
::矩形是四个右角度的四边形。 -
A
rhombus
is a quadrilateral with four congruent sides
::暴风车是四边形,四面相容 -
A
square
is a quadrilateral with four right angles and four congruent sides.
::方形是四边形,有四个右角度和四个相容的方形。
Quadrilaterals - Review Questions
::四方 - 审查问题Decide whether each statement is always, sometimes, or never true. Explain your answer.
::决定每个声明是否总是、有时是、有时是、或永远不是真实的。 请解释您的答复 。1. A square is a rectangle.
::1. 方形是一个矩形。2. A rhombus is a square.
::2. 暴风车是一个广场。3. An isosceles trapezoid is a trapezoid.
::3. 等离子体类动物是一种类动物。4. A parallelogram is a quadrilateral.
::4. 平行图是四边形。5. A square is a parallelogram.
::5. 方形是平行图。6. A trapezoid is a parallelogram.
::6. 形图是平行图。Decide what type of quadrilateral it must be and what type of quadrilateral it could be based on the description.
::决定它必须是什么类型的四边形以及它可以根据描述成为什么类型的四边形。7. A quadrilateral has 4 congruent angles.
::7. 四边形有4个相同角度。8. A quadrilateral has 2 pairs of congruent sides.
::8. 四方有两对一致的两面。9. Draw a kite. Draw in its diagonals. Make at least one conjecture about the diagonals of kites.
::9. 绘制风筝,在其对角线中绘制,至少对风筝的对角线作一个猜测。10. Draw a rectangle. Draw in its diagonals. Make at least one conjecture about the diagonals of rectangles.
::10. 绘制矩形,在对角线中绘制,至少对矩形的对角线作一个猜想。11. Draw a rhombus. Draw in its diagonals. Make at least one conjecture about the diagonals of rhombuses.
::11. 绘制圆柱,在其对角图中绘制,至少对伦布斯对角图作一个猜想。12. Draw a kite. Make a conjecture about the opposite angles of kites.
::12. 绘制风筝,对风筝的相反角度进行猜测。Use the markings on the shapes below to identify the shape. Then, solve for . Note: pictures are not drawn to scale.
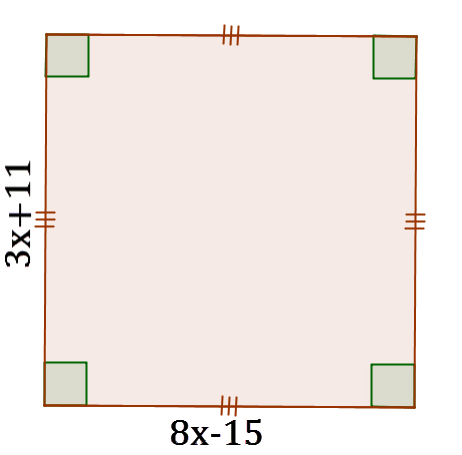
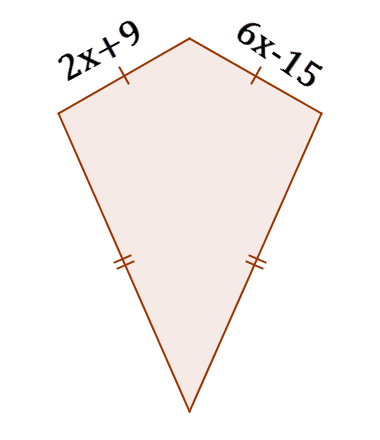
::使用下方形状上的标记来识别形状。 然后, 解决 x 。 注意: 图片不会被绘制为缩放 。13.
14.
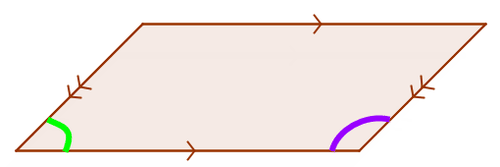
15. Make a conjecture about the adjacent angles of a parallelogram (such as the ones marked in the picture below). How must they be related?
::15. 猜测平行图的相邻角度(如下图中标注的角),它们之间如何关联?16. If a quadrilateral is a rhombus, does it have all the properties of a parallelogram? Explain.
::16. 如果四边形是圆柱形,是否具有平行图的所有特性?17. Sketch several different parallelograms. A parallelogram has many properties beyond its definition. Here are some possible properties of a parallelogram. Through experimentation with a variety of parallelograms, decide which are true or false, and explain why. Afterwards, write down a list of properties that are very likely to be true.
::17. 绘制若干不同的平行图。平行图有许多超出其定义的属性。这里是平行图的一些可能的属性。通过对各种平行图的实验,决定哪些是真实的还是虚假的,并解释原因。随后,写下非常有可能是真实的属性列表。-
Diagonals are the same length.
::对角线长度相同。 -
Opposite angles are the same measure.
::对角是相同的度量。 -
Consecutive angles are the same measure.
::连续角度是相同的量度。 -
Consecutive sides are the same length.
::后继方的长度相同。 -
Diagonals bisect each other.
::对角对立体相互交织 -
Diagonals bisect the vertex angles at their endpoints.
::对角对角将顶端角在端点上双切。 -
Opposite sides are congruent.
::对面两边是相同的。 -
Diagonals are perpendicular.
::对角是垂直的。 -
All the angles are right.
::所有的角度都是正确的。
18. Perform similar experiments with sketches of rectangles, rhombuses, squares, trapezoids, and isosceles trapezoids. Write down candidates for the properties of these figures.
::18. 以矩形、阵形、方形、形、形和等骨类类类素的草图进行类似的实验,为这些数字的特性写出候选人。Review (Answers)
::审查(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
A
kite
is a convex quadrilateral with two pairs of adjacent congruent sides such that not all sides are congruent.