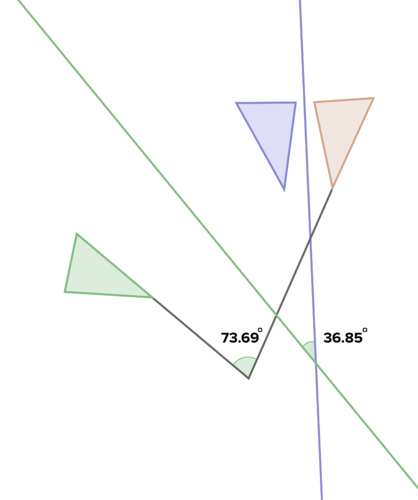节: 轮调 | 2.7 轮调-interactive

章节大纲

Rotation
::轮调

A rotation is one example of a rigid transformation .
::A 旋转是僵硬变换的一个例子。

Rotation is a geometric transformation that involves rotating a figure a certain number of degrees about a fixed point .
::旋转是一种几何变换,它涉及对固定点旋转一个数字若干度。

A positive rotation is counterclockwise and a negative rotation is clockwise.
::正旋转是逆时针,负旋转是顺时针。

Precisely speaking: A rotation of $\begin{aligned} t^{\circ} \end{aligned}$ about a given point $\begin{aligned} O \end{aligned}$ takes each point on a shape $\begin{aligned} P \end{aligned}$ and moves it to $\begin{aligned} P^{'} \end{aligned}$ such that $\begin{aligned} P^{'} \end{aligned}$ is on the circle with center $\begin{aligned} O \end{aligned}$ and radius $\begin{aligned} \bar{O P} \end{aligned}$ and $\begin{aligned} ∠ P O P^{'} = t^{\circ} . \end{aligned}$
::确切地说, 大约一个给定点 O 的旋转在形状 P 上取每点, 并移动到 P , 这样P 在圆圈上, 中间 O 和半径 OP 和 POP 。

Informally: To rotate a shape, move each point on the shape the given number of degrees around a circle centered on the point of rotation. Make sure each new point is the same distance from the point of rotation as the corresponding original point.
::非正式旋转 : 要旋转形状, 请在旋转点的圆周围移动给定的度数的形状上的每个点。请确定每个新点与旋转点的距离与相应的原始点相同。

Rotation about a point
::某个点的旋转

Below, the has been rotated $\begin{aligned} 90^{\circ} \end{aligned}$ counterclockwise about point $\begin{aligned} O \end{aligned}$ to create a new parallelogram (the image).
::下方, 已经旋转 90 / o o 点左右, 以创建新的平行图( 图像) 。

Notice point $\begin{aligned} D \end{aligned}$ rotates the specified 90 degrees around a circle centered on point $\begin{aligned} O, \end{aligned}$ so that $\begin{aligned} D^{'} \end{aligned}$ is the same distance from $\begin{aligned} O \end{aligned}$ as $\begin{aligned} D . \end{aligned}$ This process is the same for all four points in the original parallelogram.
::注意点 D 在以 O 点为中心的圆圆周围旋转指定的90度, 使 D 与 O 的距离与 D 相同。这个过程对原始平行图中的所有四个点都是一样的。

The location of point $\begin{aligned} O \end{aligned}$ is important!
::O点的位置很重要!

The parallelogram below was also rotated $\begin{aligned} 90^{\circ} \end{aligned}$ counterclockwise about point $\begin{aligned} O \end{aligned}$ , but point $\begin{aligned} O \end{aligned}$ is in a different location.
::下面的平行图在O点左右也旋转了90°Z,但O点在另一个地点。

There is a circle with center $\begin{aligned} O \end{aligned}$ that passes through each pair of corresponding points.
::有一个圆形,以O为中心,通过每一对相应的点。

Below, you can see th e angle between each point and its image is the same, centered on point $\begin{aligned} O . \end{aligned}$

::在下面,你可以看到每个点之间的角, 其图像是相同的, 以O点为中心。

Point $\begin{aligned} C \end{aligned}$ is rotated 90 degrees around $\begin{aligned} O \end{aligned}$ to be $\begin{aligned} C^{'}, \end{aligned}$ point $\begin{aligned} D \end{aligned}$ is rotated to be $\begin{aligned} D^{'}, \end{aligned}$ and so on.
::C点在O周围旋转90度,C点周围旋转90度,D点旋转D点,等等。

When describing a rotation, it is important to consider three pieces of information.
::在描述轮值时,必须考虑三点信息。

The center of rotation (point $\begin{aligned} O \end{aligned}$ in the figure above). This is the fixed point about which each point turns (the center of each circle passing through corresponding points).
::旋转中心( 上图中的点 O) 。这是每个点旋转的固定点( 每个圆圈的中心穿过相应的点) 。

T he direction of rotation . You can rotate clockwise or counterclockwise.
::旋转方向。您可以顺时针或逆时针旋转。

The degree of rotation . This tells you how much you are turning.
1. If the degrees are positive , the rotation is performed counterclockwise .
  ::如果度为正,则逆时针进行旋转。
2. If the degree measure is negative , the rotation is clockwise .
  ::如果度量为负,则旋转顺时针。
3. Remember that a full circle is $\begin{aligned} 360^{\circ} . \end{aligned}$
  ::记住圆圈是360
::旋转度。这表示您正在旋转多少。如果旋转度为正, 则逆时针进行旋转。如果测量度为负, 则顺时针进行旋转。记住一个整圆是360\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Rotation
::轮调

Select a shape with the dropdown, and then c lick or tap on the blue arrow to e xplore the rotation of the selected shape about the center of rotation $\begin{aligned} O \end{aligned}$ .
::选择一个显示下调的形状, 然后单击或点击蓝箭头, 以探索所选形状在旋转 O 中心周围的旋转。

Observe the angle of rotation, the direction of rotation and how the point being rotated moves along a circle centered at $\begin{aligned} O \end{aligned}$ .
::观察旋转的角度、旋转的方向和旋转点如何沿着以 O 为中心的一个圆圈移动。

Triangle
::三角三角形

Rotations in the coordinate plane
::坐标平面的旋转

Although a figure can be rotated any number of degrees, the rotation will often be a common angle such as $\begin{aligned} 90^{\circ}, 180^{\circ}, \end{aligned}$ or $\begin{aligned} 270^{\circ} . \end{aligned}$
::虽然一个数字可以旋转任何几度,但旋转往往是一个共同角度,如90,180,或270。

Keep in mind that if the number of degrees are positive, the figure will rotate counter-clockwise and if the number of degrees are negative, the figure will rotate clockwise. While most rotations will be centered at the origin , the figure can rotate around any given point, indicated in the problem.
::请注意, 如果度数为正数, 数字会反时针旋转, 如果度数为负数, 数字会顺时针旋转。虽然大多数旋转将以原点为中心, 但数字会围绕任何特定点旋转, 问题中已经指出。

Rotation of 90 degrees on coordinate axes.
::在坐标轴上旋转90度

Centered at origin.
::原居中心。

$\begin{aligned} (x, y) \to (- y, x) \end{aligned}$
:x,y)(-y,x)

Rotation of 180 degrees on coordinate axes.
::在坐标轴上旋转180度

Centered at origin.
::原居中心。

$\begin{aligned} (x, y) \to (- x, - y) \end{aligned}$
:x,y)(-x,-y)

Rotation of 270 degrees on coordinate axes.
::在坐标轴上旋转270度

Centered at origin.
::原居中心。

$\begin{aligned} (x, y) \to (y, - x) \end{aligned}$
:x,y)(y,-x)

CK-12 PLIX: Reflecting Figures
::CK-12 PLIX: 反映数字

Identifying and Describing Rotations
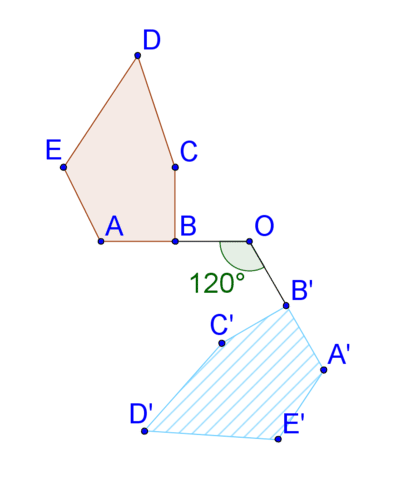
::识别和说明

1. Describe the rotation below.
::1. 以下说明轮调情况。

This is a $\begin{aligned} 135^{\circ} \end{aligned}$ counterclockwise rotation about point $\begin{aligned} O \end{aligned}$ .
::这是在 O 点左右的 135 逆时针旋转。

You could also say this is a $\begin{aligned} 225^{\circ} \end{aligned}$ ( $\begin{aligned} 360^{\circ} - 135^{\circ} \end{aligned}$ ) clockwise rotation about point $\begin{aligned} O \end{aligned}$ . Once the rotation has taken place, there is no way to know the direction of rotation.
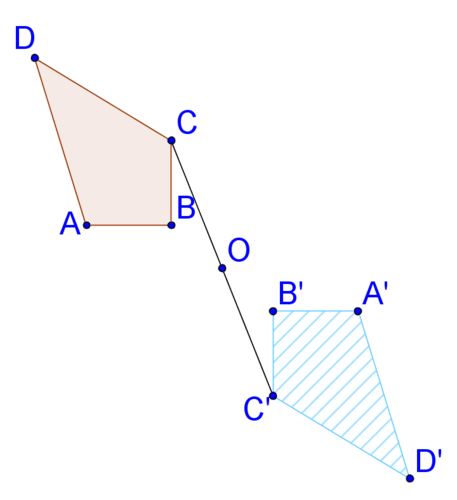
::您也可以说这是O点的顺时针旋转 225(360135) 。一旦旋转完成, 就无法知道旋转的方向。

2. Is the following transformation a rotation?
::2. 以下转型是轮流的吗?

No, while $\begin{aligned} ∠ D O D^{'} \end{aligned}$ is $\begin{aligned} 180^{\circ} \end{aligned}$ , the angles connecting other pairs of points and point $\begin{aligned} O \end{aligned}$ are not $\begin{aligned} 180^{\circ} \end{aligned}$ .
::不,虽然“DOD”是180,但连接其他两点和O点的角度不是180。

This transformation is actually a reflection across a line through point $\begin{aligned} O \end{aligned}$ , perpendicular to $\begin{aligned} \bar{D D^{'}} . \end{aligned}$
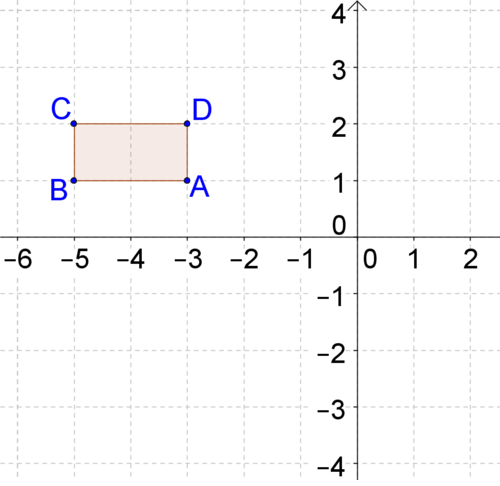
::这种转变实际上是穿过O点的直线反射, 直通到DD'''。

3. Rectangle $\begin{aligned} A B C D \end{aligned}$ is rotated $\begin{aligned} 90^{\circ} \end{aligned}$ counterclockwise about the origin. Draw the image of this rotation. How are the points of the original rectangle connected to the points of the image?
::3. 矩形 ABCD 的源值旋转 90 / obsyclock 。绘制此旋转的图像。原始矩形的点与图像点的连接如何 ?

Pick one point, such as point $\begin{aligned} A \end{aligned}$ , and draw a line segment connecting it to the origin. Because perpendicular lines form $\begin{aligned} 90^{\circ} \end{aligned}$ angles, to rotate $\begin{aligned} 90^{\circ}, \end{aligned}$ find a line perpendicular to the line segment connecting $\begin{aligned} A \end{aligned}$ to the origin. Remember that perpendicular lines have opposite reciprocal slopes. $\begin{aligned} A^{'} \end{aligned}$ will be on the perpendicular line, the same distance from the origin as $\begin{aligned} A \end{aligned}$ was.
::选择一个点, 如 A 点, 并绘制一条连接它到源的线段。因为垂直的线条组成 90 angles, 要旋转 90 , 找到一条直通连接 A 和源的线段的线条。记住 , 垂直的线条具有对等的斜坡。 A ` 将位于垂直的线条上, 与 A 的线条距离相同。

Once you have $\begin{aligned} A^{'} \end{aligned}$ , you can build the rectangle around it. $\begin{aligned} A \end{aligned}$ was at point (-3, 1) and $\begin{aligned} A^{'} \end{aligned}$ is at point (-1, -3).
::一旦有AA, 你可以在它周围建立矩形。 A在点( 3, 1) , A在点( 1, 3) 。 A在点( 1, 3) 。 A在点( 1, 3) 。

In general, a $\begin{aligned} 90^{\circ} \end{aligned}$ counterclockwise rotation about the origin takes $\begin{aligned} (x, y) \end{aligned}$ and maps it to $\begin{aligned} (- y, x) . \end{aligned}$
::一般而言, A90- o_ o o o o o o o a o a o o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a o a co co co co a co co a co a co co a co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co ro ro ro co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co ro co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co co

INTERACTIVE

Rotations

In the interactive below, move the red points to manipulate the figure. Click on the buttons to rotate the figure.
::在下面互动的交互中,移动红色点来操纵图形。单击按钮来旋转图形。

Examples
::实例实例实例实例

Example 1
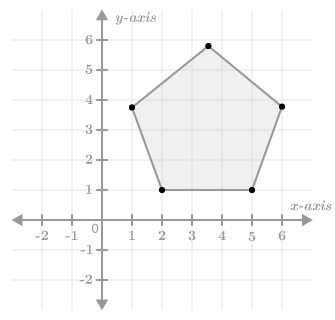
::例1

You want your friend to rotate the pentagon $\begin{aligned} 90^{\circ} \end{aligned}$ . What are the two other pieces of information you need to tell your friend to ensure that she rotates the pentagon the way you are imagining?
::您希望您的朋友旋转五角形 90 。您需要另外两个信息来告诉您的朋友, 以确保她按照您想象的那样旋转五角形 ?

To make sure your friend correctly rotates the pentagon $\begin{aligned} 90^{\circ} \end{aligned}$ , you need to also tell her the center of rotation and the direction of rotation.
::为了确保你的朋友正确旋转五角形90, 您也需要告诉她旋转的中心和旋转的方向。

Example 2
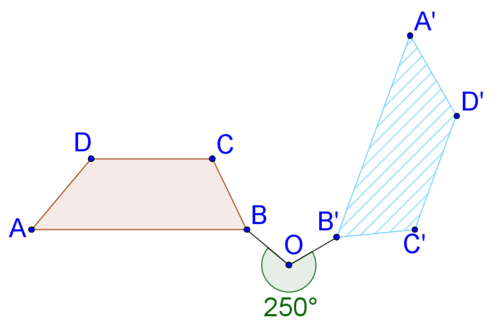
::例2

Describe the rotation below.
::以下说明轮调情况。

This is a $\begin{aligned} 135^{\circ} \end{aligned}$ clockwise rotation about point $\begin{aligned} B \end{aligned}$ .
::这是在 B 点的 135 时钟方向旋转。

You could also say this is a $\begin{aligned} 225^{\circ} \end{aligned}$ ( $\begin{aligned} 360^{\circ} - 135^{\circ} \end{aligned}$ ) counterclockwise rotation about point $\begin{aligned} B \end{aligned}$ .
::您也可以说这是B点的逆时针旋转 225(360135) 。

Example 3
::例3

Rotate the rectangle $\begin{aligned} 180^{\circ} \end{aligned}$ counterclockwise about the origin. How do the points of the original rectangle compare to their corresponding points on the image? How would your answer be different if instead you rotated $\begin{aligned} 180^{\circ} \end{aligned}$ clockwise about the origin?
::旋转矩形 180 / objectown knickwhy 有关来源的矩形。原始矩形的点如何与图像上对应的点比较? 如果您旋转了 180 / ocknown 来源, 您的答案会有什么不同 ?

There would be no difference. A rotation $\begin{aligned} 180^{\circ} \end{aligned}$ clockwise is the same as a rotation $\begin{aligned} 180^{\circ} \end{aligned}$ counterclockwise .
::不变。旋转 180 和旋转 180 相同。

You can see there is a straight line (180 degrees) passing through the origin and connecting each pair of corresponding points. The result is that the signs of each term in the ordered pairs changes: $\begin{aligned} (x, y) \to (- x, - y) . \end{aligned}$
::您可以看到一条直线( 180度) 穿过源头并连接对应的一对点。结果, 定购一对中每个词的符号会改变 x, y)% (- x, y)% (- x, y) 。

Summary

Rotation is a geometric transformation that involves rotating a figure a certain number of degrees about a fixed point.
::旋转是一种几何变换,它涉及对固定点旋转一个数字若干度。

A positive rotation is counterclockwise , and a negative rotation is clockwise .
::正旋转是逆时针,负旋转是顺时针。

When describing a rotation, consider the center of rotation, direction of rotation, and degree of rotation.
::当描述旋转时,请考虑旋转中心、旋转方向和旋转程度。

Review
::审查审查审查审查

Describe each of the following rotations in TWO ways.
::以两种方式说明下列各轮作。

lesson content

4. What does a $\begin{aligned} 360^{\circ} \end{aligned}$ rotation look like?
::4. 360的旋转长什么样?

5. Rotate the rectangle below $\begin{aligned} 90^{\circ} \end{aligned}$ clockwise about the origin.
::5. 将源代码的矩形旋转到90°Z以下。

lesson content

6. Use the previous example to help you describe what happens to a point $\begin{aligned} (x, y) \end{aligned}$ that is rotated $\begin{aligned} 90^{\circ} \end{aligned}$ clockwise about the origin.
::6. 使用上一个示例来帮助您描述一个点(x,y)发生的情况,该点在源代码上旋转了90/时。

7. (3, 2) is rotated $\begin{aligned} 90^{\circ} \end{aligned}$ clockwise about the origin. Where does it end up?
::7. (3, 2) 原产地的旋转时间为90时,最后会到哪里去?

8. (3, 2) is rotated $\begin{aligned} 180^{\circ} \end{aligned}$ clockwise about the origin. Where does it end up? Hint: Use Guided Practice #2 for help.
::8. (3, 2) 原产地按180时每小时旋转,结果在哪里? 提示: 使用指导练习 2 来帮助。

9. (3, 2) is rotated $\begin{aligned} 90^{\circ} \end{aligned}$ counterclockwise about the origin. Where does it end up? Hint: Use Example C.
::9. (3, 2) 原产地的旋转时速为90千瓦,最后会到哪里? 提示:使用例C。

10. What do circles have to do with rotations?
::10. 圆圈与轮换有什么关系?

11. $\begin{aligned} Δ A B C \end{aligned}$ is rotated $\begin{aligned} 130^{\circ} \end{aligned}$ clockwise about point $\begin{aligned} O \end{aligned}$ to create $\begin{aligned} Δ A^{'} B^{'} C^{'} \end{aligned}$ . Describe two connections between the points $\begin{aligned} B, O \end{aligned}$ , and $\begin{aligned} B^{'} \end{aligned}$ .
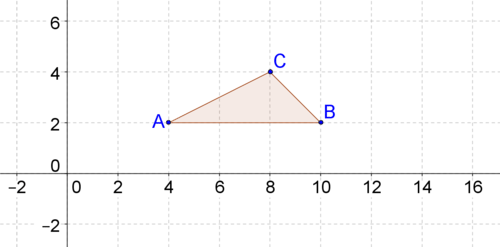
::11. QABC 旋转时速为 130, 时速为 O 点左右, 以创建 QABC。描述 BO 点和 BA 点之间的两个连接。

For 12-15, consider $\begin{aligned} Δ A B C \end{aligned}$ below.
::关于12-15,请考虑以下的“ABC”。

lesson content

12. Rotate $\begin{aligned} Δ A B C 90^{\circ} \end{aligned}$ counterclockwise about point $\begin{aligned} B \end{aligned}$ .
::12. 向B点旋转时速为ZABC 90。

13. Rotate $\begin{aligned} Δ A B C 90^{\circ} \end{aligned}$ counterclockwise about point $\begin{aligned} A \end{aligned}$ .
::13. 在A点左右时速旋转 ABC 90。

14. Rotate $\begin{aligned} Δ A B C 90^{\circ} \end{aligned}$ counterclockwise about point $\begin{aligned} C \end{aligned}$ .
::14. 逆时针旋转C点的QABC 90。

15. Could you have used the rule that a $\begin{aligned} 90^{\circ} \end{aligned}$ counterclockwise rotation takes $\begin{aligned} (x, y) \end{aligned}$ to $\begin{aligned} (- y, x) \end{aligned}$ to perform the previous three rotations? Explain.
::15. 您是否可使用90/克时针旋转(x,y)至(y,x)的规则来进行前三次旋转?解释。

16. The diagram below shows a rotation of the brown triangle to the green triangle. It shows a sequence of reflections that also maps the brown triangle to the green triangle. Explore the diagram further and explain the relationship between rotations and reflections shown there.
::16. 下图显示棕色三角向绿色三角的旋转,显示一系列映射,还绘制褐色三角向绿色三角的映射图,进一步探讨图表,并解释图中显示的旋转和反射之间的关系。

lesson content

17. What rotations map every polygon to itself? Explain. What rotations maps a line to a parallel line? Explain. What rotations map a line to itself? Explain.
::17. 什么旋转将每个多边形都映射到它本身?解释。什么旋转将线条映射到平行线条上?解释。什么旋转将线条映射到它自己身上?解释。

18. A given polygon A maps to polygon B by rotation. Is it possible to map A to B by translation? Why or why not? Is it possible to map A to B by a single reflection? Why or why not?
::18. 以旋转方式将给定多边形A地图绘制为多边形B的地图;能否用翻译方式绘制A至B?为什么不行?能否用单一的反射方式绘制A至B?为什么不行?为什么不行?能否用单一的反射方式绘制A至B的地图?为什么不行?

19. Describe and compare the translations, reflections, and rotations that map lines to themselves. Describe and compare the translations, reflections, and rotations that map angles to themselves. Describe and compare the translations, reflections, and rotations that map any polygon to itself.
::19. 描述和比较映射线的翻译、反射和旋转;描述和比较映射角度的翻译、反射和旋转;描述和比较映射任何多边形本身的翻译、反射和旋转。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Rotation ::轮调

Rotation about a point ::某个点的旋转

Rotation ::轮调

Rotations in the coordinate plane ::坐标平面的旋转

Rotation of 90 degrees on coordinate axes. ::在坐标轴上旋转90度

Rotation of 180 degrees on coordinate axes. ::在坐标轴上旋转180度

Rotation of 270 degrees on coordinate axes. ::在坐标轴上旋转270度

CK-12 PLIX: Reflecting Figures ::CK-12 PLIX: 反映数字

Identifying and Describing Rotations ::识别和说明

Examples ::实例实例实例实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::审查审查审查审查

Review (Answers) ::审查(答复)

Rotation
::轮调

Rotation about a point
::某个点的旋转

Rotation
::轮调

Rotations in the coordinate plane
::坐标平面的旋转

Rotation of 90 degrees on coordinate axes.
::在坐标轴上旋转90度

Rotation of 180 degrees on coordinate axes.
::在坐标轴上旋转180度

Rotation of 270 degrees on coordinate axes.
::在坐标轴上旋转270度

CK-12 PLIX: Reflecting Figures
::CK-12 PLIX: 反映数字

Identifying and Describing Rotations
::识别和说明

Examples
::实例实例实例实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Review
::审查审查审查审查

Review (Answers)
::审查(答复)