复合变形

播放段落

A composite transformation (or composition of transformations) is two or more transformations performed one after the other. The following is an example of a translation followed by a reflection . The original triangle is the grey triangle and the image is the blue triangle. The purple triangle shows the intermediate step after the translation has taken place.
::复合变换(或变换的构成)是两个或两个以上的变换,一个又一个。下面是翻译后反射的例子。原来的三角是灰三角,图像是蓝色三角。紫三角是翻译之后的中间步骤。

播放段落

There is no single transformation that could have replaced the composite transformation above.
::没有任何单一的转变可以取代上述综合转型。

播放段落

follow the order of operations.
::行动顺序。

播放段落
• Just as 2 + (3  $\begin{array}{r}\times \end{array}$  4) is not the same as (2 + 3)  $\begin{array}{r}\times \end{array}$  4, composite transformations must be performed in a specific order to ensure the correct result.
  ::仅仅因为2+(3×4)与(2+3×4)x4不相同,就必须具体进行复合变换,以确保正确的结果。
播放段落
• The two Compare the two methods below to see the difference.
  ::两者比较以下两种方法,以了解差异。

播放段落
1. Transform the rectangle by first rotating the rectangle $\begin{array}{r}{90}^{\text{o}}\end{array}$ counterclockwise about the origin and then translating it along vector $\begin{array}{r}\stackrel{\to }{v}.\end{array}$
   ::将矩形转换为先旋转矩形 90 ocothercondpront why 来转换源,然后将其转换为矢量 v 。

播放段落
2. Perform the same  transformations  in the other order, first translating  along vector  $\begin{array}{r}\stackrel{\to }{v},\end{array}$  and then rotating  $\begin{array}{r}{90}^{\text{o}}\end{array}$  counterclockwise.
   ::在另一顺序中执行相同的变换, 先按照矢量 v 翻译, 然后按90 o 逆时针旋转 。

播放段落

Notice that t he final images are NOT in the same place.
::注意最后的图像不在同一个地方 。

播放段落
• Transformations are not commutative.
  ::转变不是通货。
播放段落
• The order that transformations are performed matters.
  ::转换为执行事项的顺序。

---

播放段落

Mapping Shapes
::绘图形状

播放段落

Describe a possible sequence of transformations that would carry $\begin{array}{r}\mathrm{\Delta }ABC\end{array}$ to $\begin{array}{r}\mathrm{\Delta }DEF\end{array}$ .
::描述可能将 ABC 传送到 DEF 的变换序列 。

播放段落

Option 1 : A  $\begin{array}{r}{180}^{\circ }\end{array}$ rotation about a point directly in between points $\begin{array}{r}C\end{array}$ and  $\begin{array}{r}D.\end{array}$
::备选案文1:在C点和D点之间直接对一个点进行180的旋转。

播放段落

Option 2: A  reflection across $\begin{array}{r}AC\end{array}$ followed by reflection across a vertical line .
::备选办法2:在丙烷之间进行反射,然后在垂直线上进行反射。

播放段落

Option 3: Another possibility is that $\begin{array}{r}\mathrm{\Delta }ABC\end{array}$ was rotated $\begin{array}{r}{180}^{\circ }\end{array}$ about point $\begin{array}{r}C\end{array}$ and then translated to $\begin{array}{r}\mathrm{\Delta }DEF.\end{array}$
::备选案文3:另一种可能性是,在C点附近旋转了ABC180,然后翻译为ZDEF。

播放段落

These are only three possible descriptions of the transformation. Can you think of another?
::这些只是三个可能的变换描述。你能想到另一个吗?

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

A reflection followed by a translation where the line of reflection is parallel to the direction of translation is called a glide reflection or a walk. Why do you think this is?
::反射,然后是翻译,反射线与翻译方向平行,反射被称为滑翔反射或步行。你认为这是为什么?

播放段落

It is called a glide reflection or a walk because it's as if the shape was reflected and then glided over to a new location. When done repeatedly, the shapes look like footsteps walking.
::它被称为滑翔反射或散步, 因为它仿佛形状被反射, 然后滑行到一个新的位置。如果反复进行, 形状看起来像脚步行走。

播放段落

Example 2
::例2

播放段落

Transform the triangle by first reflecting across $\begin{array}{r}\overline{AC}\end{array}$ and then across the line perpendicular to $\begin{array}{r}\overline{AC}\end{array}$ through $\begin{array}{r}C\end{array}$ . What one transformation could you have performed to get the same result?
::将三角形转换为首先反射到AC,然后跨过直线直通AC至C。你能够做出什么改变才能获得相同结果?

播放段落

A $\begin{array}{r}{180}^{\circ }\end{array}$ rotation about point $\begin{array}{r}C\end{array}$ would have produced the same result.
::180C点的旋转会产生同样的结果。

Summary

播放段落 A composite transformation is two or more transformations performed one after the other. ::复合变换是两个或两个以上的变换,一个又一个地变换。 播放段落 Composite transformations follow order of operations, meaning the order in which transformations are performed matters. ::复合变换遵循操作顺序,即变换的顺序。 播放段落 Mapping shapes involves describing a sequence of transformations that would carry one shape to another. ::绘图形状涉及描述一个变异序列,这些变异将携带一个形状到另一个形状。 播放段落 Multiple sequences of transformations can result in the same final image. ::多重变换序列可能导致相同的最终图像。

---

播放段落

1. What is a composite transformation?
::1. 什么是综合转变?

播放段落

2. When doing a composite transformation, does the order in which you perform the transformations matter?
::2. 在进行复合变换时,进行变换的顺序是否重要?

播放段落

3. Describe a possible sequence of transformations that would carry   $\begin{array}{r}\mathrm{\Delta }ABC\end{array}$  to   $\begin{array}{r}\mathrm{\Delta }DEF\end{array}$ .
::3. 描述可能将ABC运至ZDEF的变异序列。

播放段落

4. Describe another possible sequence of transformations that would carry   $\begin{array}{r}\mathrm{\Delta }ABC\end{array}$  to   $\begin{array}{r}\mathrm{\Delta }DEF\end{array}$ .
::4. 描述另一个可能将ABC传送到ZDEF的变异序列。

播放段落

5. Describe a possible sequence of transformations that would carry   $\begin{array}{r}\mathrm{\Delta }GHI\end{array}$  to   $\begin{array}{r}\mathrm{\Delta }JKL\end{array}$ .
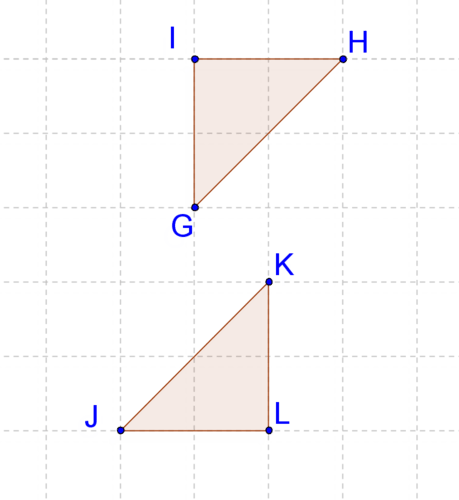
::5. 描述可能将GHI运至ZQKL的变异序列。

播放段落

6. Describe another possible sequence of transformations that would carry   $\begin{array}{r}\mathrm{\Delta }GHI\end{array}$  to   $\begin{array}{r}\mathrm{\Delta }JKL\end{array}$ .
::6. 描述可能将GHI运至ZQKL的另一种变异序列。

播放段落

7. Describe a possible sequence of transformations that would carry   $\begin{array}{r}\mathrm{\Delta }MNO\end{array}$  to   $\begin{array}{r}\mathrm{\Delta }PQR\end{array}$ .
::7. 描述一个可能将QQR-MNO 传送到QR 的可能变换序列。

播放段落

8. Describe another possible sequence of transformations that would carry   $\begin{array}{r}\mathrm{\Delta }MNO\end{array}$  to   $\begin{array}{r}\mathrm{\Delta }PQR\end{array}$ .
::8. 描述另一组可能进行的转换序列,这些转换将把QQR和MNO移到QR。

播放段落

9. Construct a polygon on graph paper or with   interactive geometry software .
::9. 在图形纸上或用交互式几何软件构建多边形。

播放段落

10. Reflect the polygon twice across parallel lines. What one transformation could you have performed to get the same result?
::10. 多边形在平行线上反射两次。您能用什么转换来取得相同结果?

播放段落

11. Reflect the polygon twice across another set of parallel lines. What one transformation could you have performed to get the same result?
::11. 将多边形两次反射到另一组平行线上。您能够完成何种变换来取得相同结果?

播放段落

12. Make a conjecture by completing the sentence. Two reflections across parallel lines is the same as a ______________.
::12. 通过完成句子作出推测:两个平行的反省与一个反省相同。

播放段落

13. Reflect the polygon twice across intersecting lines (not necessarily perpendicular). What one transformation could you have performed to get the same result?
::13. 将多边形两次反射为横跨交叉线(不一定是垂直的),为了获得相同结果,你能够做出什么改变?

播放段落

14. Make a conjecture by completing the sentence. Two reflections across intersecting lines is the same as a ______________.
::14. 通过完成句子作出推测:横跨交叉线的两种反射与______相同。

播放段落

15. Given any translation, is it possible to accomplish the same result through a series of reflections? If so, describe them in detail. Use  interactive geometry software   to experiment.
::15. 鉴于任何译文,能否通过一系列反思实现同样的结果?如果可以,请详细描述这些结果。使用交互式几何软件进行实验。

播放段落

16. Given any rotation, is it possible to accomplish the same result through a series of reflections? If so, describe them in detail. Use  interactive geometry software  to experiment.
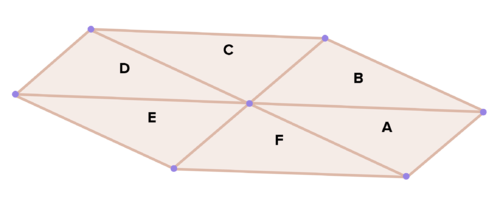
::16. 鉴于任何轮换,能否通过一系列反思实现同样的结果?如果可以,请详细描述这些结果。使用互动几何软件进行实验。

播放段落

17. Describe sequences of transformations that map the triangles in the diagram below to each other.
::17. 描述将图中三角形映射在下图中的转换顺序。

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。