Congruent三角应用

播放段落

Two triangles are congruent if and only if their corresponding sides and are congruent.
::两个三角形是相同的,如果而且只有对应的两边是相同的,并且是一致的。

播放段落

Here are  the criteria that can be used to show triangle congruence :
::以下是用来显示三角一致的标准 :

播放段落
• AAS (Angle-Angle-Side) : If two triangles have two pairs of congruent angles , and a non-common (not shared) side in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent.
  ::AAS( 角- 角- 斜角) : 如果两个三角有两对相近角度, 而一个三角内一个非常见( 不共享) 的侧面与另一个三角内对应的侧面相匹配, 那么三角形是相匹配的 。
播放段落
• ASA (Angle-Side-Angle): If two triangles have two pairs of congruent angles and the common side of the angles (the side between the congruent angles) in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent.
  ::ASA( Agle- Side- Agle) : 如果两个三角形有两对相近角度, 一个三角形中角的普通侧面( 相近角度之间的侧面) 与另一个三角形的对应侧面相匹配, 那么三角形是相近的 。
播放段落
• (Side-Angle-Side): If two triangles have two pairs of congruent sides and the included angle (the angle between the congruent sides) in one triangle is congruent to the included angle in the other triangle, then the triangles are congruent.
  ::如果两个三角形有两对一致的两边,而一个三角形中包含的角(相同两边之间的角)与另一个三角形中包含的角一致,则三角形是相同的。
播放段落
• (Side-Side-Side): If two triangles have three pairs of congruent sides, then the triangles are congruent.
  ::如果两个三角形有三对一致的两边,那么三角形是相同的。
播放段落
• Right triangles only:   (Hypotenuse-Leg): If two right triangles have one pair of legs congruent and hypotenuses congruent, then the triangles are congruent.
  ::仅右三角形Hypotenuse-Leg):如果两个右三角形有一对双腿相容和一对下角相容,则三角形是相容的。

播放段落

If two triangles don't satisfy at least one of the criteria above, you cannot be confident that they are congruent.
::如果两个三角形不能至少满足上述标准之一, 你就不能相信它们是一致的。

---

播放段落

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

---

播放段落

Recognizing Perpendicular Bisectors
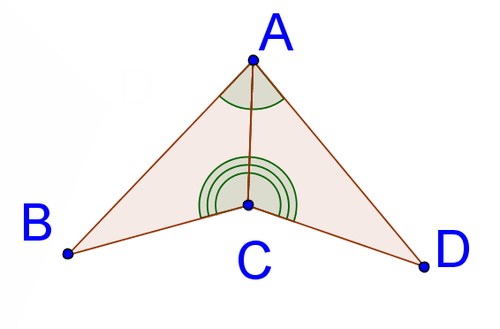
::承认垂直两侧部门

播放段落

In the triangle below,  $\begin{align*}\overline{BC}\end{align*}$ is the perpendicular bisector of $\begin{align*}\overline{AD}.\end{align*}$   Therefore   $\begin{align*}\overline{AC}\cong \overline{CD}\end{align*}$ . Also, $\begin{align*}m\angle ACB=90^\circ\end{align*}$ and $\begin{align*}m\angle DCB=90^\circ,\end{align*}$  so $\begin{align*}\angle ACB \cong \angle DCB\end{align*}$ . You also know that $\begin{align*}\overline{BC}\end{align*}$ is a side of both triangles, and is clearly congruent to itself (this is called the reflexive property).
::在下面的三角形中, BC 是AD 的直角两侧。 因此, AC = CD 。 另外, m ACB = 90\\ 和 m DCB= 90\ 。 所以 ACB = DCB = 90\ 。 您也知道 BC 是两个三角形的一面, 而且与自己明显一致( 这被称为反射属性 ) 。

播放段落

The triangles are congruent by SAS. Note that even though these are right triangles, you would not use HL to show triangle congruence in this case since you are not given that the hypotenuses are congruent.
::SAS 的三角形是相似的。 请注意, 即使这些三角形是正确的三角形, 您也不会使用 HL 来显示三角形在此情况下的一致性, 因为您没有被赋予下限值是相同的 。

---

播放段落

Measuring Angles
::测量角度

播放段落

Using the information from the previous problem, if $\begin{align*}m\angle A=50^\circ\!,\end{align*}$  what is $\begin{align*}m\angle D?\end{align*}$
::使用上一个问题的信息,如果mA=50,什么是mD?

播放段落

$\begin{align*}m\angle D=50^\circ\end{align*}$
::mD=50

播放段落

Since the triangles are congruent, all of their corresponding angles and sides must be congruent. $\begin{align*}\angle A\end{align*}$ and $\begin{align*}\angle D\end{align*}$ are corresponding angles, so $\begin{align*}\angle A \cong \angle D.\end{align*}$
::由于三角形是相同的, 所有相应的角度和侧面必须是相同的。 @ @A和QD是相应的角度, 所以 @AQD 。 @AQD

---

播放段落

Congruent Triangles
::共成三角形

播放段落

Does one diagonal of a rectangle divide the rectangle into congruent triangles?
::矩形的对角将矩形分割成相容三角形吗?

播放段落
• Recall that a rectangle is a quadrilateral with four right angles.
  ::回顾矩形是四边形,有四个右角度。
播放段落
• The opposite sides of a rectangle are congruent.
  ::矩形对面的两面是相似的。

播放段落

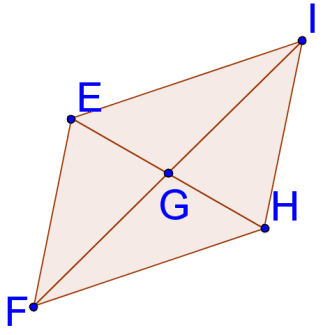
There is more than enough information to show that $\begin{align*}\triangle EFG \cong \triangle GHE.\end{align*}$ .
::足够多的信息显示这“EFGGHE”。

播放段落
• Method #1: The triangles have three pairs of congruent sides, so they are congruent by SSS .
  ::方法1:三角形有三对一致的两面,因此它们与SSS是相同的。
播放段落
• Method #2: The triangles have two pairs of congruent sides and congruent included angles , so they are congruent by SAS .
  ::方法#2:三角形有两对相容的两边和相近的包括角度,因此它们与SAS一致。
播放段落
• Method #3: The triangles are right triangles with congruent hypotenuses and a pair of congruent legs, so they are congruent by HL .
  ::方法# 3:三角形是右三角形, 与相近的下限和一双相近的腿, 所以它们与 HL 相匹配 。

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

Max constructs a triangle using an online tool. He tells Alicia that his triangle has a $\begin{align*}42^\circ\end{align*}$  angle, a side of length 12 and a side of length 8. With only this information, will Alicia be able to construct a triangle that must be congruent to Max's triangle?
::Max 使用在线工具构建三角形 。 他告诉 Alicia 他的三角形有42角, 12长的一面和8长的一面 。 只有这一信息 Alicia 才能构建一个三角形, 必须与 Max 的三角形相匹配吗 ?

播放段落

If Max also told Alicia that the angle was in between the two sides, then she would be able to construct a triangle that must be congruent due to SAS. If the angle is not between the two sides, she cannot be confident that her triangle is congruent because SSA is not a criterion for triangle congruence. Because Max did not state where the angle was in relation to the sides, Alicia cannot create a triangle that must be congruent to Max's triangle. 
::如果Max还告诉Alicia说角度在两边,那么她就可以建造一个由于SAS而必须一致的三角形。如果角度不是在两边,她就不能确信三角形是一致的,因为SSA不是三角一致的标准。由于Max没有说明角度与两边的关系,Alicia不能建立一个必须与Max的三角形一致的三角形。

播放段落

Example 2
::例2

播放段落

Are the following triangles congruent? Explain.
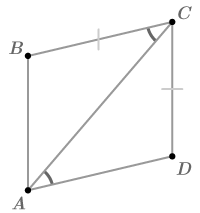
::以下三角形是否一致?解释。

播放段落

Notice that besides the one pair of congruent sides and the one pair of congruent angles, $\begin{align*}\overline{AC}\cong \overline{CA}.\end{align*}$
::注意除了一对一致的两面 和一对一致的角外,ACCA。

播放段落

$\begin{align*}\triangle ACB \cong \triangle CAD \end{align*}$ by SAS . 
::由SAS的ACBCAD。

播放段落

Example 3
::例3

播放段落

Are the following triangles congruent? Explain.
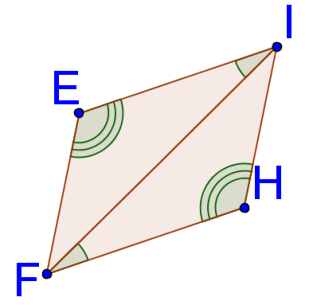
::以下三角形是否一致?解释。

播放段落

The congruent sides are not corresponding in the same way that the congruent angles are corresponding. The given information for $\begin{align*}\triangle ACB\end{align*}$ is SAS while the given information for $\begin{align*}\triangle CAD\end{align*}$ is SSA. The triangles are not necessarily congruent.
::相容的两面不和对齐的角度相同。 QACB 的给定信息为 SAS , 而给定的信息为 SSA 。 三角不一定一致 。

播放段落

Example 4
::例4

播放段落

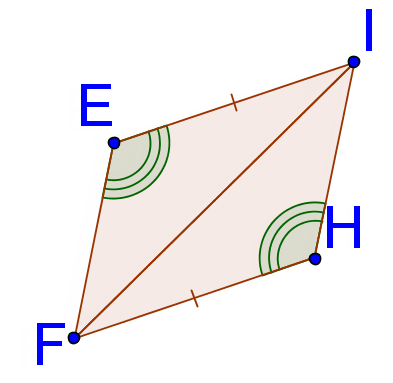
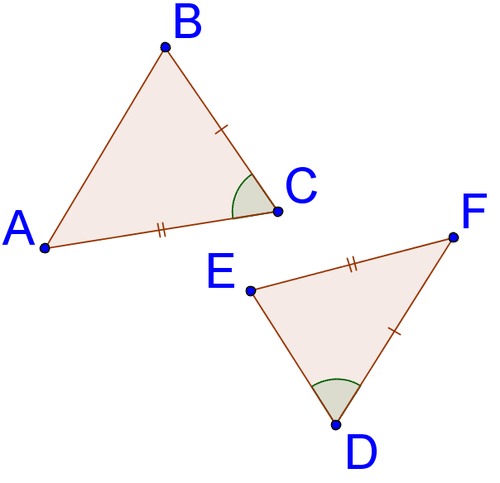
$\begin{align*}G\end{align*}$ is the midpoint of $\begin{align*}\overline{EH}\end{align*}$ . Are the following triangles congruent? Explain.
::G 是 EH 的中点。 以下三角形是否相似? 解释 。

播放段落

Because $\begin{align*}G\end{align*}$ is the midpoint of $\begin{align*}\overline{EH}\end{align*}$ , $\begin{align*}\overline{EG}\cong \overline{GH}\end{align*}$ . You also know that $\begin{align*}\angle EGF \cong \angle HGI\end{align*}$ because they are . $\begin{align*}\triangle EGF \cong \triangle HGI\end{align*}$ by ASA . 
::因为G是EH的中点 你也知道EGOHGI 因为他们是ASA的EGOHGI

Remember this!

播放段落 HL (Hypotenuse-Leg) (For right triangles only): If two right triangles have one pair of legs congruent and hypotenuses congruent, then the triangles are congruent. ::HL (Hypotenuse-Leg) (仅指右三角形): 如果两个右三角形的双腿相近, 下角相匹配, 那么三角形是相匹配的 。 播放段落 Side-side-side (SSS) criterion states that if two triangles have three pairs of congruent sides, then the triangles are congruent. ::侧边标准(SSS)规定,如果两个三角形有三对相近的两边,三角形是相近的。 播放段落 Side-Angle-Side (SAS) criterion states that if two triangles have two pairs of congruent sides and the included angle in one triangle is congruent to the included angle in the other triangle, then the triangles are congruent. ::侧角-侧角-侧角(SAS)标准规定,如果两个三角形有两对相容的两对角,而一个三角形中包括角的角与另一个三角形中包含角的角一致,则三角形是相容的。 播放段落 Angle-Side-Angle (ASA) criterion states that if two triangles have two pairs of congruent angles and the common side of the angles in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent. ::角度- 角度- 角度( ASA) 标准指出, 如果两个三角具有两对相容角度, 一个三角的角的正向侧与另一个三角的对角相匹配, 那么三角是相容的 。 播放段落 A ngle-Angle-Side (AAS) criterion states that if two triangles have two pairs of congruent angles and the opposite side of the angles in one triangle is congruent to the corresponding side in the other triangle, then the triangles are congruent. ::角度- 角度- 角度- 角度( AAS) 标准表示, 如果两个三角有两对相近角度, 而一个三角中角的对面与另一个三角中对应的侧面相匹配, 那么三角是相近的 。

---

播放段落

Review
::审查审查审查审查

播放段落

1. List the five criteria for triangle congruence and draw a picture that demonstrates each.
::1. 列出三角一致的五项标准,并绘制显示每一方的图画。

播放段落

2. Given two triangles, do you always need at least three pieces of information about each triangle in order to be able to state that the triangles are congruent?
::2. 对于两个三角形,你是否总是需要至少三个三角形的信息,才能说明三角形是相同的?

播放段落

For each pair of triangles, tell whether the given information is enough to show that the triangles are congruent. If the triangles are congruent, state the criterion that you used to determine the congruence and write a congruency statement.
::对于每对三角形,请说明给定的信息是否足以显示三角形是相同的。如果三角形是相同的,请说明您用来确定一致性的标准,并写出一致的语句。

播放段落

Note that the images are not necessarily drawn to scale.
::请注意,图像不一定被绘制成比例。

3.

4.

5.

6.

7.

8.

播放段落

For 9-11, state whether the given information about a hidden triangle would be enough for you to construct a triangle that must be congruent to the hidden triangle. Explain your answer.
::对于 9- 11, 声明给定的关于隐藏三角形的信息是否足够您构建一个必须与隐藏三角形一致的三角形。 请解释您的答复 。

播放段落

9. $\begin{align*}\triangle ABC\end{align*}$ with $\begin{align*}m\angle A=72^\circ\end{align*}$ , $\begin{align*}AB=6 \ \text{cm}\end{align*}$ , $\begin{align*}BC=8 \ \text{cm}.\end{align*}$
::9. ABC, mA=72,AB=6厘米,BC=8厘米。

播放段落

10. $\begin{align*}\triangle ABC\end{align*}$ with $\begin{align*}m\angle A=90^\circ\end{align*}$ , $\begin{align*}AB=4 \ \text{cm}\end{align*}$ , $\begin{align*}BC=5 \ \text{cm}.\end{align*}$
::10. ABC, mA=90,AB=4厘米,BC=5厘米。

播放段落

11. $\begin{align*}\triangle ABC\end{align*}$ with $\begin{align*}m\angle A=72^\circ\end{align*}$ , $\begin{align*}AB=6 \ \text{cm}\end{align*}$ , $\begin{align*}AC=8 \ \text{cm}.\end{align*}$
::11. ABC, mA=72,AB=6厘米,AC=8厘米。

播放段落

12. Recall that a square is a quadrilateral with four right angles and four congruent sides. Show and explain why a diagonal of a square divides the square into two congruent triangles.
::12. 回顾一个广场是四边形,有四个右角度和四个正方形,显示并解释一个广场的对角将广场分为两个正方形三角。

播放段落

13. Show and explain using a different criterion for triangle congruence why a diagonal of a square divides the square into two congruent triangles.
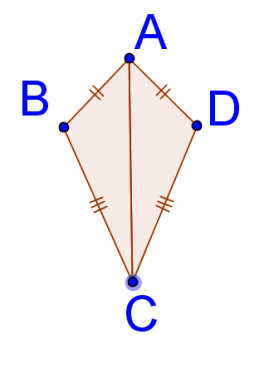
::13. 使用不同的三角一致标准显示和解释为什么一个正方形的对角将方形分为两个正方形的对角三角。

播放段落

14. Recall that a kite is a quadrilateral with two pairs of adjacent, congruent sides. Will one of the diagonals of a kite divide the kite into two congruent triangles? Show and explain your answer.
::14. 回顾风筝是四边形,有两对相邻、相近的对立面,风筝的对立面之一能否将风筝分为两个对立三角形?显示并解释你的答复。

播放段落

15. In the picture below, $\begin{align*}G\end{align*}$ is the midpoint of both $\begin{align*}\overline{EH}\end{align*}$ and $\begin{align*}\overline{FI}\end{align*}$ . Explain why $\begin{align*}\overline{FH}\cong \overline{IE}\end{align*}$ and $\begin{align*}\overline{FE}\cong \overline{HI}\end{align*}$ .
::15. 如下图所示,G是EH和FI的中点,请解释为什么FAI和FEH HI。

播放段落

16. Explain why AAA is not a criterion for triangle congruence.
::16. 解释为什么AAA不是三角一致的标准。

播放段落

Review (Answers) 
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。