节: 圆形的切线线 | 8.7 到圆形的切线-interactive

章节大纲

When a line intersects a circle in exactly one point the line is said to be tangent to the circle or a tangent of the circle. This point is called the point of tangency .
::当一线在一点内将一圆相交时,该线据说与圆相切,或圆的正切。此点被称为相切点。

INTERACTIVE

Tangent Lines to Circles

Move the red point to change the size of the red circle. Move the blue point to see different possible positions of the blue circle. Both the red and blue circles share the gray tangent.
::移动红色点以改变红圆的大小。移动蓝色点以看到蓝色圆的不同位置。红圆和蓝色圆都使用灰色正切线。

You will prove that if a tangent line intersects a circle at point $\begin{aligned} P \end{aligned}$ , then the tangent line is perpendicular to the radius drawn to point $\begin{aligned} P \end{aligned}$ .
::您将证明,如果正切线在 P点交叉圆,则正切线与P点的半径垂直。

From any point outside a circle, you can draw two lines tangent to the circle. You will learn how to construct these lines in problems later. Below, from point $\begin{aligned} C \end{aligned}$ both lines $\begin{aligned} l \end{aligned}$ and $\begin{aligned} m \end{aligned}$ are tangent to circle $\begin{aligned} A \end{aligned}$ .
::从圆外的任何一点, 您可以在圆上绘制两行切线。您以后会学习如何在问题中构造这些线条。下面, 从 C 点 l 线和 m 线都切线到 A 圈。

Diagram shows tangent lines l and m touching circle at points P and A, respectively.

In the second problem, y ou will show that in this situation, $\begin{aligned} \bar{P C} ≅ \bar{C Q} \end{aligned}$ . In the third problem, you will show that $\begin{aligned} ∠ P A Q \end{aligned}$ and $\begin{aligned} ∠ P C Q \end{aligned}$ are supplementary.
::在第二个问题中,你将显示,在这种情况下,PC QQ。在第三个问题中,你将显示,QPAQ和QPCQ是补充性的。

Let's look at a few example problems.
::让我们看看几个例子问题。

1. Line $\begin{aligned} l \end{aligned}$ is tangent to circle $\begin{aligned} A \end{aligned}$ at point $\begin{aligned} P \end{aligned}$ . Prove that line $\begin{aligned} l \end{aligned}$ is perpendicular to $\begin{aligned} \bar{A P} \end{aligned}$ .
::1. 线与P点圆A的线相切。证明这条线与AP的垂直。

This proof relies on the fact that the shortest distance from a point to a line is along the segment perpendicular to the line.
::这一证据所依据的事实是,从一个点到一条线的最短距离与直线垂直的段段相邻。

Consider a point $\begin{aligned} Q \end{aligned}$ on line $\begin{aligned} l \end{aligned}$ but not on circle $\begin{aligned} A \end{aligned}$ . $\begin{aligned} A Q > A P \end{aligned}$ , because $\begin{aligned} Q \end{aligned}$ is outside circle $\begin{aligned} A \end{aligned}$ . This means that the shortest distance from line $\begin{aligned} l \end{aligned}$ to point $\begin{aligned} A \end{aligned}$ is from point $\begin{aligned} P \end{aligned}$ to point $\begin{aligned} A \end{aligned}$ . Therefore, $\begin{aligned} \bar{A P} \end{aligned}$ must be perpendicular to line $\begin{aligned} l \end{aligned}$ .
::考虑一线的Q点,但不考虑A.A.A.A.AP圆的Q点,因为Q是圆A。这意味着从一线到A点的最短距离是从P点到A点。因此,AP'必须与一线垂直。

2. From point $\begin{aligned} C \end{aligned}$ , both lines $\begin{aligned} l \end{aligned}$ and $\begin{aligned} m \end{aligned}$ are tangent to circle $\begin{aligned} A \end{aligned}$ . Show that $\begin{aligned} \bar{P C} ≅ \bar{Q C} \end{aligned}$ . What does this mean in general?
::2. 从C点看,I线和m线都与A圈相切,显示PC {C}。这一般意味着什么?

Draw a segment connecting $\begin{aligned} A \end{aligned}$ and $\begin{aligned} C \end{aligned}$ . Note that $\begin{aligned} ∠ A Q C \end{aligned}$ is also a right angle .
::绘制连接 A 和 C 的段。请注意 AQC 也是一个右角度。

$\begin{aligned} \bar{A C} ≅ \bar{A C} \end{aligned}$ by the reflexive property and $\begin{aligned} \bar{P A} ≅ \bar{Q A} \end{aligned}$ because they are both radii of the circle. This means that $\begin{aligned} △ A P C ≅ △ A Q C \end{aligned}$ by $\begin{aligned} H L ≅ \end{aligned}$ . $\begin{aligned} \bar{P C} ≅ \bar{Q C} \end{aligned}$ because the segments are corresponding parts of congruent triangles.
::CC AC 由反射属性和 PA A 组成,因为它们都是圆形的半径。这意味着 HL 的 APC QC 。 PC PC QC , 因为各部分是相近三角形的对应部分。

$\begin{aligned} \bar{P C} \end{aligned}$ and $\begin{aligned} \bar{Q C} \end{aligned}$ are known as tangent segments. In general, two tangent segments to a circle from the same point outside the circle will always be congruent.
::PC 和 QC 被称为正切区段。一般来说, 两个相切区段到圆圈, 从圆圈外的同一点到圆圈, 总是一致的。

3. From point $\begin{aligned} C \end{aligned}$ , both lines $\begin{aligned} l \end{aligned}$ and $\begin{aligned} m \end{aligned}$ are tangent to circle $\begin{aligned} A \end{aligned}$ . Show that $\begin{aligned} ∠ P A Q \end{aligned}$ and $\begin{aligned} ∠ P C Q \end{aligned}$ are supplementary. What does this mean in general?
::3. 从C点看,一行和米线与圆A相切。显示“PAQ”和“PCQ”是补充性的。

$\begin{aligned} ∠ A Q C \end{aligned}$ is a right angle because line $\begin{aligned} m \end{aligned}$ is tangent to circle $\begin{aligned} A \end{aligned}$ at point $\begin{aligned} Q \end{aligned}$ . The sum of the measures of the interior angles of a quadrilateral is $\begin{aligned} 360^{\circ} \end{aligned}$ . This means that
::+QQC 是一个右角度, 因为线M 与 Q 点的圆 A 相切。四边形内角的测量总和是 360 。这意味着

$\begin{aligned} m ∠ P A Q \end{aligned}$ $\begin{aligned} + \end{aligned}$ $\begin{aligned} m ∠ A Q C \end{aligned}$ $\begin{aligned} + \end{aligned}$ $\begin{aligned} m ∠ P C Q \end{aligned}$ $\begin{aligned} + \end{aligned}$ $\begin{aligned} m ∠ C P A \end{aligned}$ $\begin{aligned} = 360^{\circ} . \end{aligned}$
::mPAmAQC+mPCmCPA=360。

$\begin{aligned} m ∠ P A Q + m ∠ P C Q = 360^{\circ} - 90^{\circ} - 90^{\circ} = 180^{\circ} \end{aligned}$ .
::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

Therefore, $\begin{aligned} ∠ P A Q \end{aligned}$ and $\begin{aligned} ∠ P C Q \end{aligned}$ are supplementary.
::因此,“PAQ”和“PCQ”是补充性的。

In general, the angle between two lines tangent to a circle from the same point will be supplementary to the central angle created by the two tangent lines.
::一般而言,两条正切线与同一点的圆之间的角,是对两条正切线所创造的中心角的补充。

Construct Tangents through an External Point
::通过外部点构造定点

Use your compass and straightedge (or another construction device) to construct a circle and a point not on the circle. Label the center of the circle $\begin{aligned} A \end{aligned}$ and the point not on the circle $\begin{aligned} C \end{aligned}$ . Draw the line $\begin{aligned} A C \end{aligned}$ .
::使用您的指南针和直方( 或其他构造设备) 来构造圆, 而不是圆上的一个点。标签是圆 A 的中心, 而不是圆 C 的中心。绘制线性AC 。

Construct the perpendicular bisector of $\begin{aligned} A C \end{aligned}$ in order to find its midpoint , $\begin{aligned} M \end{aligned}$ .
::构造 AC 的垂直对角, 以便找到中点 M 。

Then construct a circle centered at point $\begin{aligned} M \end{aligned}$ that passes through point $\begin{aligned} C \end{aligned}$ . The circle should also pass through point $\begin{aligned} A \end{aligned}$ .
::然后在M点建造一个圆圈,穿过C点。圆圈也应该穿过A点。

Find the points of intersection and connect them with point $\begin{aligned} C \end{aligned}$ .
::找到交叉点并将其与C点连接起来。

Note that $\begin{aligned} A C \end{aligned}$ is a diameter of circle $\begin{aligned} M \end{aligned}$ , so it divides circle $\begin{aligned} M \end{aligned}$ into two semicircles. $\begin{aligned} ∠ A P C \end{aligned}$ and $\begin{aligned} ∠ A Q C \end{aligned}$ are inscribed angles of these semicircles, so they must be right angles. $\begin{aligned} P C \end{aligned}$ meets radius $\begin{aligned} A P \end{aligned}$ at a right angle, so $\begin{aligned} P C \end{aligned}$ is tangent to circle $\begin{aligned} A \end{aligned}$ . Similarly, $\begin{aligned} Q C \end{aligned}$ meets radius $\begin{aligned} A Q \end{aligned}$ at a right angle, so $\begin{aligned} Q C \end{aligned}$ is tangent to circle $\begin{aligned} A \end{aligned}$ .
::请注意, AC 是圆 M 的直径, 所以它将圆 M 分成两个半圆形。 QAPC 和 QAQC 是这些半圆形的刻度角, 所以它们必须是右角。 PC 在右角与半圆 AP 相匹配, 所以 PC 与圆 A 相切。同样, QC 在右角与半圆 AQ 相匹配, 所以 QC 与圆 A 相切。

Examples
::实例实例实例实例

Example 1
::例1

$\begin{aligned} \overset{\leftrightarrow}{D C} \end{aligned}$ and $\begin{aligned} \overset{\leftrightarrow}{C E} \end{aligned}$ are tangent to circle $\begin{aligned} A \end{aligned}$ at points $\begin{aligned} D \end{aligned}$ and $\begin{aligned} E \end{aligned}$ respectively. What type of quadrilateral is $\begin{aligned} A D C E \end{aligned}$ ? Can you find $\begin{aligned} m ∠ D C E \end{aligned}$ ?
::DC 和 CE 分别与 D 点和 E 点的 A 圆相切。 ADCE 是哪一种四边形? 您能找到 mDCE 吗 ?

$\begin{aligned} \bar{D A} \end{aligned}$ and $\begin{aligned} \bar{E A} \end{aligned}$ are both radii of the circle, so they are congruent. $\begin{aligned} \bar{D C} \end{aligned}$ and $\begin{aligned} \bar{E C} \end{aligned}$ are both tangent segments to the circle from the same point $\begin{aligned} (C) \end{aligned}$ , so they are congruent. The quadrilateral has two pairs of adjacent congruent segments so it is a .
::DA 和 EA 均为圆形的半边形, 因此它们是一致的。 DC 和 EC 是从同一个点( C) 到圆形的正切部分, 所以它们都是正切的。四边形有两对相邻的相近相近部分, 所以它是一个。

$\begin{aligned} m \hat{D E} \end{aligned}$ $\begin{aligned} = 360^{\circ} - 238^{\circ} = 122^{\circ} \end{aligned}$ . The means $\begin{aligned} m ∠ D A E \end{aligned}$ $\begin{aligned} = 122^{\circ} \end{aligned}$ . Because $\begin{aligned} \overset{\leftrightarrow}{D C} \end{aligned}$ and $\begin{aligned} \overset{\leftrightarrow}{C E} \end{aligned}$ are tangent to circle $\begin{aligned} A \end{aligned}$ , you know that $\begin{aligned} ∠ D A E \end{aligned}$ and $\begin{aligned} ∠ D C E \end{aligned}$ are supplementary . $\begin{aligned} m ∠ D C E = 180^{\circ} - 122^{\circ} = 58^{\circ} \end{aligned}$ .
::mDE360238122。这意味着 mDAE=122。因为 DC和CE与A圈相切,你知道 DAE和ZDCE是补充的。 mDCE=18012258。

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

Summary

A tangent line is a line that intersects a circle in exactly one point.
::相切线是将圆交错于一点的直线。

A tangent line intersects a circle at point P, then the tangent line is perpendicular to the radius drawn to point P.
::相切线在 P 点交叉圆,则正切线与P 点的半径垂直。

Review
::审查审查审查审查

1. What is a tangent line to a circle?
::1. 圆形的正切线是什么?

For all pictures below, assume that lines that appear tangent are tangent. For questions #2 through #7 round your answers to the nearest hundredths place where needed.
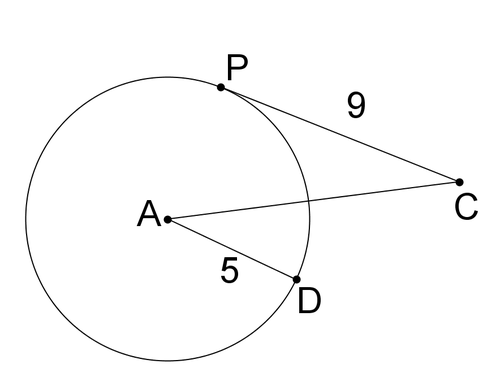
::对于下面的所有图片, 假设显示相切的线是正切的。对于问题2到7, 您在需要的地方将答案绕到最近的一百个地方。

Use the image below for #2-#3.
::使用下面的图像显示 # 2 # 3 。

2. Draw in $\begin{aligned} \bar{A P} \end{aligned}$ and find its length.
::2. 在AP中绘制并找到其长度。

3. Find $\begin{aligned} \bar{A C} \end{aligned}$
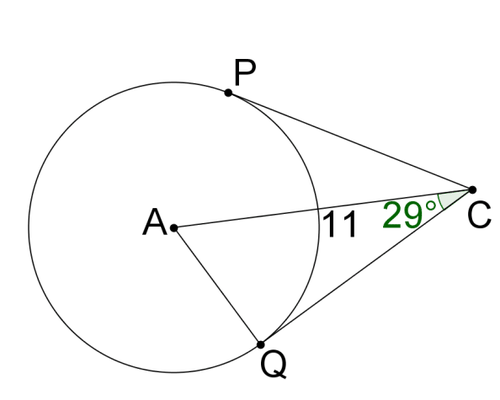
::3. 寻找AC

Use the image below for #4-#7.
::使用下面的图象显示 # 4 - # 7 。

4. Find $\begin{aligned} m ∠ C A Q \end{aligned}$
::4. 寻找 mCAQ

5. Find $\begin{aligned} \bar{A Q} \end{aligned}$
::5. 寻找AQ

6. Find $\begin{aligned} \bar{Q C} \end{aligned}$
::6. 找到QC

7. Find $\begin{aligned} \bar{P C} \end{aligned}$
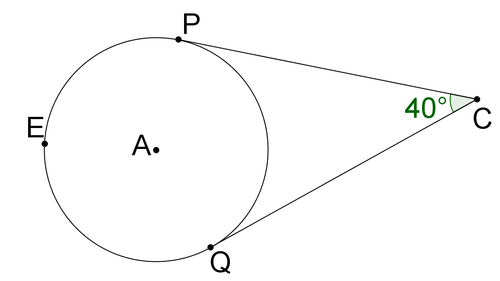
::7. 寻找PC

Use the image below for #8-#9.
::使用下面的图像显示 # 8- # 9 。

8. Find $\begin{aligned} m \hat{P Q} \end{aligned}$
::8. 寻找 mP

9. Find $\begin{aligned} m \hat{P E Q} \end{aligned}$
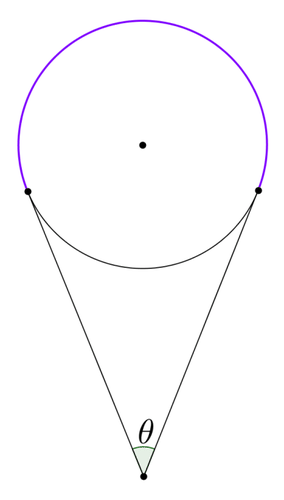
::9. 寻找 mPE

Use the image below for #10-#11. Also note that 62% of the circle is purple.
::使用下面的图像为 # 10 - # 11 。请注意, 62% 的圆是紫色。

10. Find the measure of the purple arc.
::10. 找出紫弧的量度。

11. Find the measure of angle $\begin{aligned} θ \end{aligned}$ .
::11. 寻找角度的度量。

Use the image below for #12-#13.
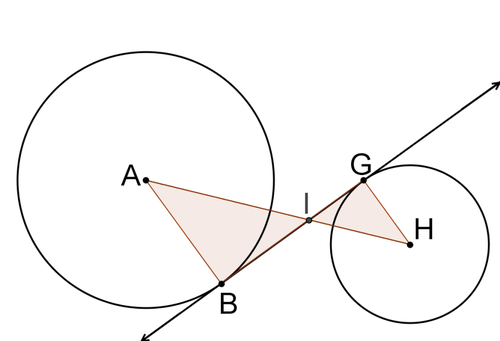
::使用下面的图像为 # 12- # 13 服务。

12. Make a conjecture about how $\begin{aligned} △ A B I \end{aligned}$ and $\begin{aligned} △ H G I \end{aligned}$ are related.
::12. 猜测一下“ABI”和“HGI”之间的关系。

13. Prove your conjecture from #12.
::13. 证明你12号的猜想。

14. Use construction tools of your choice to construct a circle and a point not on the circle. Then, construct two lines tangent to the circle that pass through the point. Hint: Look at the Guided Practice questions for the steps for this construction.
::14. 使用你选择的建筑工具来建造圆圈,而不是圆圈上的圆点,然后在穿过圆圈的圆圈上建造两条正切线。

15. Justify why your construction from #14 created tangent lines.
::15. 说明为什么你从14号建筑中产生了相切的线条。

16. How many tangents can be drawn to a circle containing a point outside the circle? Explain. What if the tangent(s) contained a point inside the circle? What if the tangent(s) contained a point on the circle?
::16. 圆外含有点的圆圈可画出多少正切点?解释:如果正切点含有圆内的一个点,如何?如果圆上的正切点含有圆上的一个点,怎么办?

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Construct Tangents through an External Point ::通过外部点构造定点

Examples ::实例实例实例实例

Example 1 ::例1

CK-12 PLIX Interactive ::CK-12 PLIX 交互式互动

Review ::审查审查审查审查