圆柱体

播放段落

Below is a rectangular prism and a cylinder . Note that the height of each solid is the same.
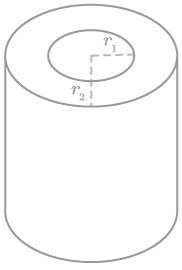
::下面是一个矩形棱柱和一个圆柱体。请注意,每块固体的高度是一样的。

播放段落

In each case, the area of the base is $\begin{array}{r}\pi r^2\end{array}$ . In fact, the area of any cross section taken parallel to the base is $\begin{array}{r}\pi r^2\end{array}$ . Because these solids have the same height and the same cross sectional areas at every level, the solids have the same volume due to Cavalieri's principle.
::在每种情况下,基座的面积为°r2。 事实上,与基座平行的任何跨区面积为°r2。 由于这些固体的高度与每层的高度相同,跨区面积相同,由于卡瓦列里尼的原则,这些固体的体积相同。

播放段落

The of the prism is:
::棱镜的特征是:

播放段落

$\begin{array}{r}{V}_{\text{prism}}=A_{\text{base}}\cdot h=\pi r^{2}h\end{array}$
::Vprism = Abasehr2h = Abasehr2h

播放段落

Therefore, the volume of the cylinder is:
::因此,气瓶的体积是:

播放段落

$\begin{array}{r}{V}_{\text{cylinder}}=\pi r^{2}h\end{array}$
::Vcylinderr2h

播放段落

This should make sense because a cylinder is essentially a circular prism. The area of its base is $\begin{array}{r}\pi r^2\end{array}$ and its height is $\begin{array}{r}h\end{array}$ , so its volume is $\begin{array}{r}\pi r^{2}h\end{array}$ .
::这应该有道理,因为圆柱体基本上是圆棱镜。其基底面积为°r2,高度为h,其体积为°r2h。

播放段落

Let's take a look at a problem about how volume is related to radius and height.
::让我们来研究一下 体积与半径和高度 有何关联的问题。

播放段落

The two cylinders below have the same radius and the same height. Do they have the same volume?
::下面的两个气瓶的半径相同,高度相同。它们的体积相同吗?

播放段落

Yes, due to Cavalieri's principle. Even though these two cylinders are different, because they have the same height and base (and because every parallel cross section is congruent to the base), their volumes will be the same. The “slanted” cylinder is called an oblique cylinder.
::是的,由于卡瓦列里尼的原则。 尽管这两个圆筒是不同的,因为它们的高度和基底相同(而且因为每个平行的交叉区段都与基底一致 ) , 它们的体积也是一样的。 “倾斜”圆筒被称为斜体圆筒。

---

播放段落

Cylinder
::圆柱体

播放段落

Click the small blue arrow next to the image below and then drag the orange dots to reshape the cylinders. Note in an oblique cylinder, the bases are parallel to each other, but the sides make an angle that is not $\begin{array}{r}{90}^{\circ }\end{array}$ . If they are at $\begin{array}{r}{90}^{\circ }\end{array}$ to the bases, it is called a right cylinder.
::单击下方图像旁边的小蓝箭头, 然后拖动橙色点重塑圆柱体。 在斜体圆柱体中注意, 基座是平行的, 但两边的角不是 90\\\\。 如果在 90\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

---

播放段落

Finding Volume
::查找量

播放段落

1. Find the volume of the cylinders given below .
::1. 查找下列圆柱体的体积。

播放段落

The volume of each cylinder is $\begin{array}{r}{V}_{\text{cylinder}}=\pi r^{2}h=\pi (2{)}^2(4)=16\pi {\text{in}}^3\end{array}$ .
::每个圆柱体的体积为Vcylinderr2h(2)2(4)=16英寸。

播放段落

2. One cup of water has a volume of approximately $\begin{array}{r}14.44{\text{in}}^3\end{array}$ . How many cups of water will the cylinders in the first problem hold?
::2. 一杯水的体积大约为14.44英寸。 第一个问题中的气瓶将有多少杯水?

播放段落

The volume of each cylinder is $\begin{array}{r}16\pi {\text{in}}^3\approx 50.2655{\text{in}}^3\end{array}$ . Since each cup of water has a volume of $\begin{array}{r}14.44{\text{in}}^3\end{array}$ , each cylinder will hold $\begin{array}{r}\frac{50.2655}{14.44}\approx 3.5\end{array}$ cups of water.
::由于每杯水的体积为14.44英寸,每瓶水的体积为15.5514.44英寸3.5英寸。

---

播放段落

Examples
::实例实例实例实例

播放段落

Example 1
::例1

播放段落

Cavalieri's principle states that if two solids lying between parallel planes have equal heights and all cross sections at equal distances from their bases have equal areas, then the solids have equal volumes. Why does this make sense?
::卡瓦列里尼的原则指出,如果平行平面之间的两块固体的高度相等,而且所有交叉段与基地的距离相等,其面积相等,那么固体的体积相等。 为什么这有意义?

播放段落

One way to understand Cavalieri's principle is to imagine a stack of books. Each stack of books below is made up of 15 books. The volume of each stack is the same because the books in each stack are the same. Each stack of books has the same height, and the areas are the same at each cross section that is parallel to the base. Even though the second stack of books is slanted, the volumes are the same.

::理解卡瓦列里尼原则的一种方法就是想象一叠书。 下面的每叠书由15本书组成。 每堆书的体积相同, 因为每堆书都是相同的。 每堆书的体积相同, 每一堆书的体积也相同, 每个交叉段的面积相同, 与底部平行。 尽管第二堆书被倾斜, 但书的体积相同 。

播放段落

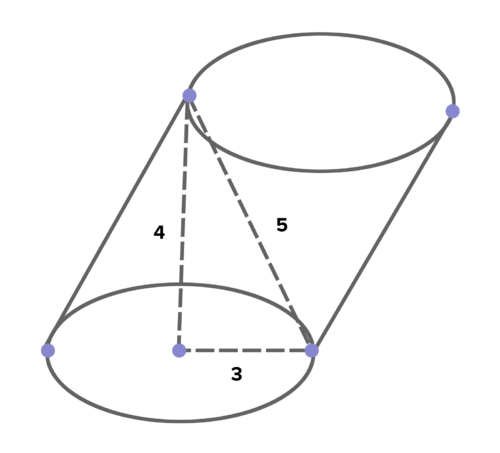
Are the volumes of the two cylinders below the same?
::两个气瓶的容量是否低于相同的水平?

播放段落

No. The height of the oblique cylinder will be less than its slant height of 4 inches. Because the overall height of the two cylinders is not the same, the volumes will be different. Remember that when calculating the volume, the height you use must be perpendicular to the base.
::否。 斜体圆柱体的高度将小于其倾斜高度4英寸。 由于两个圆柱体的总高度不同, 体积会不同。 记住, 当计算体积时, 您使用的高度必须与基底垂直。

播放段落

Example 3
::例3

播放段落

A cylinder is removed from the center of a larger cylinder as shown below.
::如下文所示,一个气瓶从一个较大的气瓶的中心移走。

播放段落

The radius of the cylinder that was removed is 3 inches. The radius of the large cylinder is 6 inches. The height of the solid is 12 inches. What is the volume of the solid that remains?
::移除的圆柱体半径为 3 英寸。 大圆柱体半径为 6 英寸。 固体的高度为 12 英寸。 剩余固体的体积是多少?

播放段落

The volume of the original large cylinder is $\begin{array}{r}\pi r_1^{2}h=\pi (6{)}^2(12)=432\pi {\text{in}}^3\end{array}$ .
::原大气瓶的体积为12h(6)2(12)=432英寸3。

播放段落

The volume of the cylinder that was removed is $\begin{array}{r}\pi r_2^{2}h=\pi (3{)}^2(12)=108\pi {\text{in}}^3\end{array}$ .
::去除的圆柱体体积为+22h(3)2(12)=108英寸3。

播放段落

The volume of the remaining solid is $\begin{array}{r}432\pi -108\pi =324\pi {\text{in}}^3\end{array}$ .
::剩余固体的体积为3,4321083243。

播放段落

Example 4
::例4

播放段落

How many cups of water will the solid from Example #3 hold?
::从例3中取出的固体能支撑多少杯水?

播放段落

Recall that a cup of water has a volume of approximately $\begin{array}{r}14.44{\text{in}}^3\end{array}$ . The volume of the solid from Example 3 is $\begin{array}{r}324\pi \approx 1017.876{\text{in}}^3\end{array}$ . It will hold $\begin{array}{r}\frac{1017.876}{14.44}\approx 70.5\end{array}$ cups of water. One gallon of water is 16 cups, so this solid will hold approximately $\begin{array}{r}\frac{70.5}{16}=4.4\end{array}$ gallons of water.
::回顾每杯水的体积大约为14.44英寸,3 例3的固体体积为3241017.876英寸,将持有1017.87614.4470.5杯水,一加仑水为16个,因此,每加仑水的体积大约为70.516=4.4加仑水。

播放段落

CK-12 PLIX Interactive
::CK-12 PLIX 交互式互动

Summary

播放段落 A cylinder is a solid with congruent circular bases that are in parallel planes. The space between the circles is enclosed. A cylinder has a radius, a height, and can also be oblique (slanted). ::一个圆柱体是一个固态的圆形圆形基体,在平行平面上是相同的圆形基体。圆圈之间的空间是封闭的。圆圆柱体有一个半径,一个高度,也可以是斜斜的(斜斜的)。 播放段落 The volume of a prism is $\begin{array}{r}V=\text{area of the base}\times \text{height}\end{array}$   ::棱晶的体积是基x58的V=区域 播放段落 The volume of a cylinder is $\begin{array}{r}V=A\times h=\pi r^{2}h\end{array}$   ::气瓶的体积为 V=Axhr2h

---

播放段落

1. Explain Cavalieri's principle in your own words.
::1. 用你自己的话解释卡瓦列里的原则。

播放段落

2. What is the volume of a slanted cylinder?
::2. 倾斜圆柱体的体积是多少?

播放段落

3. Explain how the volume of a cylinder relates to the volume of a prism.
::3. 解释圆柱体的体积与棱晶体积的关系。

播放段落

Find the volume of each cylinder with the given dimensions. Keep your answers in terms of  $\begin{array}{r}\pi .\end{array}$
::以给定尺寸查找每个圆柱体的体积。 请保留您的回答 。

4.

5.

播放段落

6. A cylinder with a base diameter of 15 inches and a height of 12 inches.
::6. 基直径为15英寸、高度为12英寸的圆筒。

播放段落

7. A cylinder with a base diameter of 8 centimeters and a height of 2 centimeters.
::7. 基直径为8厘米、高度为2厘米的圆筒。

播放段落

8. Find the radius of the base of a cylinder with a volume of $\begin{array}{r}150\pi {\text{in}}^3\end{array}$ and a height of 6 inches.
::8. 找出气瓶底部半径150°in3,高度6英寸。

播放段落

9. Find the radius of the base of a cylinder with a volume of $\begin{array}{r}432\pi {\text{in}}^3\end{array}$ if the height of the cylinder is twice the length of the radius.
::9. 如果圆柱体的高度是圆柱体半径的两倍,则找出圆柱体的底部半径,其体积为432in3。

播放段落

10. Find the height of a cylinder with a base area of $\begin{array}{r}25\pi {\text{in}}^2\end{array}$ if the volume of the cylinder is $\begin{array}{r}300\pi {\text{in}}^3\end{array}$ .
::10. 如果圆柱体体积为300英寸3,则查找基面积为25°x英寸2的圆柱体的高度。

播放段落

11. The label on a can of juice is missing. You want to know how many cups are in the can of juice. You measure the diameter of the base of the can and find that it is 5 inches. You measure the height of the can and find that it is 8 inches. If $\begin{array}{r}14.44{\text{in}}^3\end{array}$ is about 1 cup of liquid, how many cups of juice are in the can? Use 3.14 for $\begin{array}{r}\pi \end{array}$  and round your answer to the nearest hundredths place.
::11. 果汁罐的标签缺失。您想知道果汁罐中有多少杯子; 您测量罐子底部的直径, 并发现罐子的直径是5英寸; 您测量罐子的高度, 并发现罐子的高度是8英寸; 如果14. 44英寸3是大约1杯液体, 罐子里有多少杯子? 使用3. 14 , 然后将答案绕到最近的一百个地方 。

播放段落

12. A cylinder has been removed from the center of another cylinder. The volume of the remaining solid is $\begin{array}{r}240\pi {\text{in}}^3\end{array}$ . If the height of the solid is 3 inches and the radius of the cylinder that was removed is 8 inches, what is the radius of the larger cylinder?
::12. 一个圆柱体已从另一个圆柱体的中心移走,其余固体的体积为240英寸,如果固体的高度是3英寸,被移走的圆柱体半径是8英寸,大圆柱体的半径是多少?

播放段落

13. Imagine that the solid from the previous question is a ring-like water tank (i.e. a cylindrical tank with the center cylinder removed). How many cups of water can fit in this ring-like tank? Note that one cup of liquid has a volume of approximately  $\begin{array}{r}14.44{\text{in}}^3.\end{array}$ Use 3.14 for $\begin{array}{r}\pi \end{array}$  and round your answer to the nearest hundredths place.
::13. 想象一下,上一个问题的固体是一个环状水箱(即一个圆柱体罐,取下圆柱体圆柱体圆柱体),有多少杯水可以装在这个环形水箱里?请注意,一杯液体的体积约为14.44英寸3. 使用3.14, 并绕过你回答最近的一百个地方。

播放段落

For questions 14 and 15 note that 1 cubic centimeter ( $\begin{array}{r}{\text{cm}}^3\end{array}$ or cc) will hold 1 milliliter (mL) of liquid. Approximately how much liquid will each cylinder hold in liters? Use 3.14 for  $\begin{array}{r}\pi \end{array}$ and round your answer to the nearest thousandths place.
::问题14 和 15 请注意 1 立方厘米( 立方厘米或cc) 将持有 1 毫升 液体 。 每个气瓶 的 立方升 大约 多少 液体 ? 使用 3. 14 表示 ° , 并环绕您 的 答案到 最近的千 点 。

14.

15.

播放段落

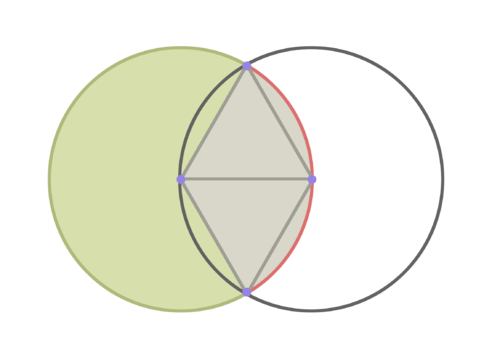
16. Consider the following construction. The two circles shown share a radius of length 1 cm. Describe the triangles shown and find their area. Describe the sectors shown and find their area. Use these values to help you determine the total area of the overlapping circles. Use 3.14 for  $\begin{array}{r}\pi \end{array}$  in each calculation and round your answers to the nearest thousandths place.
::16. 考虑以下构造:显示的两个圆圈的半径长度为1厘米。描述显示的三角形并找到其区域;描述显示的区段并找到其区域;使用这些数值帮助您确定重叠圆圈的总面积;在每次计算中使用3.14, 并围绕您对最接近千位的回答来计算 。

播放段落

17. Imagine constructing a figure composed of two overlapping cylinders with a base as visualized above. Make a sketch. Find its volume and surface area.
::17. 想象一个由两个重叠的圆筒组成的数字,其基数如上图所示,绘制一个草图,找出其体积和表面面积。

播放段落

18. Use the metaphor of a stack of coins to explain the formula for the volume of a right cylinder versus that of an oblique cylinder.
::18. 用一堆硬币的比喻来解释右圆柱体体积的公式与斜圆柱体的公式。

播放段落

19. What is the centroid of a triangle? How does it relate to triangles in the real world? Given the coordinates of three vertices of a triangle, how can we find its center of mass? Create a triangle in the coordinate plane and find its center of mass.
::19. 三角形的中间体是什么?它与真实世界中的三角形有什么关系?根据三角形的三个顶端的坐标,我们如何找到它的物体中心?在坐标平面上建立一个三角形,并找到它的重量中心。

播放段落

20. The centroid of a parallelogram is the intersection of its diagonals and also its center of mass. Below is an oblique cylinder. Sketch a top view of a single "disc" or "coin" taken from the cylinder.  What is the center of mass of each disc? Now sketch a side view of the cylinder, so that the bases only appear as segments. What shape is this? Where is its center of mass? Does this center of mass apply to the cylinder? Why or why not?
::20. 平行图的圆柱体是其对角体及其质量中心的交叉点。下面是一个斜体圆柱体。 从圆柱体中绘制一个单“disc”或“coin”的顶部视图。 每个圆盘的重量中心是什么? 现在绘制一个圆柱体的侧面视图, 使基座只显示为区块。 这是什么形状? 其质量中心在哪里? 这个质量中心是否适用于圆柱体? 为什么不行?

播放段落

Review (Answers)
::审查(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。