节: 指点分隔线线线段 | 10.6 分区线线段的点-interactive

章节大纲

Suppose you have a line segment $\begin{aligned} \bar{A B} \end{aligned}$ . A point $\begin{aligned} P \end{aligned}$ divides this line segment into two parts such that $\begin{aligned} A P \end{aligned}$ $\begin{aligned} = m k \end{aligned}$ and $\begin{aligned} P B \end{aligned}$ $\begin{aligned} = n k \end{aligned}$ . You can say that point $\begin{aligned} P \end{aligned}$ partitions segment $\begin{aligned} A B \end{aligned}$ in a $\begin{aligned} m : n \end{aligned}$ ratio . (Note that $\begin{aligned} \frac{m k}{n k} = \frac{m}{n} \end{aligned}$ , a ratio of $\begin{aligned} m : n \end{aligned}$ .)
::假设您有一个直线段 AB 。点 P 将该直线段分为两部分, 以便AP=mk 和 PB=nk 。您可以用 m:n 比例表示点 P 分区段 AB 。 (注意 mknk=mn, 比例 m:n 。 )

A natural question to ask is, what are the coordinates of point $\begin{aligned} P \end{aligned}$ ? It turns out that with the help of similar triangles and algebra, you can come up with a formula that will give you the coordinates of point $\begin{aligned} P \end{aligned}$ based on the coordinates of $\begin{aligned} A \end{aligned}$ , the coordinates of $\begin{aligned} B \end{aligned}$ , and the ratio $\begin{aligned} m : n \end{aligned}$ . This formula is sometimes referred to as the section formula.
::要问的自然问题是,P点的坐标是什么?事实证明,在类似的三角形和代数的帮助下,你可以提出一个公式,根据A点的坐标、B点的坐标和 m:n 的比,给您提供P点的坐标。这个公式有时被称为区域公式。

Proving Triangle Similarity
::证明三角形相似性

For segment $\begin{aligned} \bar{A B} \end{aligned}$ below, draw two right triangles , one with hypotenuse $\begin{aligned} \bar{A P} \end{aligned}$ and one with hypotenuse $\begin{aligned} \bar{P B} \end{aligned}$ . Show that these triangles are similar .
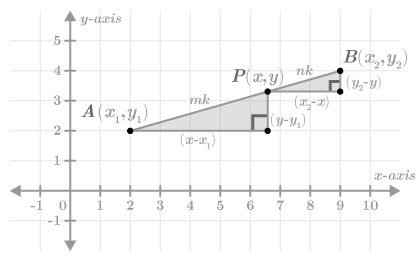
::对于下面的 AB 段, 请绘制两个右三角形, 一个是按下AP , 一个是按下PB 。显示这些三角形相似。

Start by drawing the right triangles . Below, the base and height of each triangle has been labeled in gray.
::开始绘制右三角形。下面, 每个三角形的底部和高度被标记为灰色。

Clearly these triangles have one pair of congruent angles (the right angles). What other information do you have about the triangles? You know that for each triangle, the ratio $\begin{aligned} \frac{height}{base} \end{aligned}$ is the slope of $\begin{aligned} \bar{A B} \end{aligned}$ . Because these two triangles are attached to the same line segment with the same slope, it means that $\begin{aligned} \frac{h_{1}}{b_{1}} = \frac{h_{2}}{b_{2}} \end{aligned}$ . This is equivalent to $\begin{aligned} \frac{b_{2}}{b_{1}} = \frac{h_{2}}{h_{1}} \end{aligned}$ . Two pairs of sides are in the same ratio.
::显然,这些三角具有一对相近角度(右角度) 。关于三角形, 您还有什么其他信息 ? 您知道, 对于每个三角形, 比率高度基准是 AB 的斜坡。因为这两个三角形与同一斜坡连接在同一条线段上, 这意味着 h1b1=h2b2, 这相当于 b2b1=h2h2h1。两对边是相同的比例。

Not only is there one pair of congruent angles , but there are also two pairs of corresponding sides with the same ratio. The triangles are similar by $\begin{aligned} S A S \sim \end{aligned}$ .
::不仅有一对一致的角度,而且有两对对应的两对对应的边,比例相同。三角形与SAS相似。

Finding Length and Height
::查找长度和高度

Find the lengths of the bases and heights of each triangle. Use the fact that the triangles are similar to set up and solve proportions for $\begin{aligned} x \end{aligned}$ and then for $\begin{aligned} y \end{aligned}$ in order to find the coordinates of point $\begin{aligned} P \end{aligned}$ .
::查找每个三角形的底部和高度的长度。使用三角形相似于为 x 和 y 设置和解析比例的事实来查找点 P 的坐标。

The bases and heights can be found in terms of $\begin{aligned} x_{1} \end{aligned}$ , $\begin{aligned} y_{1} \end{aligned}$ , $\begin{aligned} x \end{aligned}$ , $\begin{aligned} y \end{aligned}$ , $\begin{aligned} x_{2} \end{aligned}$ , $\begin{aligned} y_{2} \end{aligned}$ .
::以 x1 y1, x, y, x2, y2 y2 表示的基数和高度。

Because the triangles are similar, the ratios between pairs of corresponding sides are equal. In particular, you know:
::由于三角形相似,对应两边对对比是相等的。特别是,你知道:

$\begin{aligned} \frac{m k}{n k} = \frac{x - x_{1}}{x_{2} - x} \end{aligned}$
::mknk=x-x1x2-x

$\begin{aligned} \frac{m k}{n k} = \frac{y - y_{1}}{y_{2} - y} \end{aligned}$
::mknk=y-y1y2-yy

You can use algebra to solve the first equation for $\begin{aligned} x \end{aligned}$ and the second equation for $\begin{aligned} y \end{aligned}$ .
::您可以使用代数来解析 x 的第一个方程式和 y 的第二个方程式。

Point $\begin{aligned} P \end{aligned}$ is at:
::P点在:

$\begin{aligned} P = (\frac{m x_{2} + n x_{1}}{m + n}, \frac{m y_{2} + n y_{1}}{m + n}) \end{aligned}$
::P=(mx2+nx1m+n,my2+ny1m+n)

Finding the Coordinates of a Point
::查找点的坐标

Consider $\begin{aligned} \bar{A B} \end{aligned}$ with $\begin{aligned} A = (10, 2) \end{aligned}$ and $\begin{aligned} B = (4, 1) \end{aligned}$ . $\begin{aligned} P \end{aligned}$ partitions $\begin{aligned} \bar{A B} \end{aligned}$ in a ratio of 2:3. Find the coordinates of point $\begin{aligned} P \end{aligned}$ .
::以 A=( 10, 2) 和 B=( 4, 4, 1) 考虑AB 表示, P分区 AB 的比例为 2 : 3. 找到点 P 的坐标。

You can use the section formula with $\begin{aligned} (x_{1}, y_{1}) = (10, 2) \end{aligned}$ , $\begin{aligned} (x_{2}, y_{2}) = (4, 1) \end{aligned}$ , $\begin{aligned} m = 2 \end{aligned}$ , $\begin{aligned} n = 3 \end{aligned}$ .
::您可以使用(x1,y1)=(10,2),(x2,y2)=(4,4,1),(m=2),=3的区段公式。

$\begin{aligned} P = (\frac{m x_{2} + n x_{1}}{m + n}, \frac{m y_{2} + n y_{1}}{m + n}) & = (\frac{2 \cdot 4 + 3 \cdot 10}{2 + 3}, \frac{2 \cdot 1 + 3 \cdot 2}{2 + 3}) \\ = (7.6, 1.6) \end{aligned}$
::P=(mx2+nx1m+n,my2+ny1m+n)=(24+3102+3,21+3×22+3)=(7.6,1.6)

You can plot points $\begin{aligned} A \end{aligned}$ , $\begin{aligned} B \end{aligned}$ and $\begin{aligned} P \end{aligned}$ to see if this answer is realistic.
::你可以绘制A、B和P点,看这个答案是否现实。

This does look like $\begin{aligned} P \end{aligned}$ partitions the segment from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} B \end{aligned}$ in a ratio of 2:3. Note that the answer would be different if you were looking for the point that partitioned the segment from $\begin{aligned} B \end{aligned}$ to $\begin{aligned} A \end{aligned}$ . The order of the letters and "direction" of the segment matters.
::这看起来像P 分割区段从 A 到 B 的比例是 2 : 3. 请注意,如果您在寻找从 BtoA 分隔区段的点, 答案将会不同。字母的顺序和分区事项的“ 方向 ” 。

Examples
::实例实例实例实例

Example 1

::例1

The midpoint formula is a special case of the section formula where $\begin{aligned} m = n = 1. \end{aligned}$ Derive a formula that calculates the midpoint of the segment connecting $\begin{aligned} (x_{1}, y_{1}) \end{aligned}$ with $\begin{aligned} (x_{2}, y_{2}) . \end{aligned}$
::中点公式是部分公式的一个特例,其中 m=n=1. 生成一个公式,计算连接(x1,y1)和(x2,y2)的段段的中点。

For a midpoint, $\begin{aligned} m = n = 1. \end{aligned}$ The section formula becomes:
::对于中点, m=n=1. 区域公式为:

$\begin{aligned} (\frac{m x_{2} + n x_{1}}{m + n}, \frac{m y_{2} + n y_{1}}{m + n}) = (\frac{x_{2} + x_{1}}{2}, \frac{y_{2} + y_{1}}{2}) \end{aligned}$
:mx2+nx1m+n,my2+ny1m+n)=(x2+x12,y2+y12)

This is the .
::这是。。。

Example 2
::例2

A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the side opposite the vertex. All triangles have three and these three medians intersect in one point called the centroid , shown below. The centroid partitions each median in a 2:1 ratio.
::三角形的中位数是一条线段,该线段将三角形的顶点与顶点对面的侧端的中点连接起来。所有三角形都有三个中间点,而这三个中位点在一个点上交叉,称为中位点,即以下所示的中位点。中位点间段每个中位数为2:1。

Find the coordinates of the centroid, given the coordinates of the vertices of the triangle as shown.
::查找中心机器人的坐标, 并给定显示的三角形顶端的坐标。

One way to find the coordinates of the centroid is to use the section formula. You can focus on any of the three . Here, look at the median from point $\begin{aligned} A \end{aligned}$ . First, you will need to find the coordinates of the midpoint of $\begin{aligned} \bar{B C} \end{aligned}$ .
::找到中间体坐标的一个方法就是使用区域公式。您可以聚焦于三个公式中的任何一个。这里, 从 A 点看中位数。首先, 您需要找到 BC 中点的坐标。

$\begin{aligned} (\frac{x_{2} + x_{1}}{2}, \frac{y_{2} + y_{1}}{2}) = (\frac{5 + 6}{2}, \frac{5 + 1}{2}) = (5.5, 3) \end{aligned}$
:x2+x12,y2+y12)=(5+62,5+12)=(5.5,3)

Now, you want to find the point that partitions the segment from $\begin{aligned} (x_{1}, y_{1}) = (2, 6) \end{aligned}$ to $\begin{aligned} (x_{2}, y_{2}) = (5.5, 3) \end{aligned}$ in a 2:1 ratio $\begin{aligned} (m = 2, n = 1) \end{aligned}$ .
::现在, 您想要找到一个点, 将段段从 (x1, y1) = (2, 6) 到 (x2, y2) = (5. 5, 3) 的分隔点, 比例为 2:1 (m=2, n=1) 。

$\begin{aligned} (\frac{m x_{2} + n x_{1}}{m + n}, \frac{m y_{2} + n y_{1}}{m + n}) & = (\frac{2 \cdot 5.5 + 1 \cdot 2}{2 + 1}, \frac{2 \cdot 3 + 1 \cdot 6}{2 + 1}) \\ = (\frac{13}{3}, 4) \end{aligned}$
:mx2+nx1m+n,my2+ny1m+n) = (2.5.5+122+1,2}3+1) =(133 400)

Looking at the picture, these coordinates for the centroid are realistic.
::看着图片,这些座标的机器人是现实的。

Example 3
::例3

The midpoint of a line segment is the point exactly in the middle of the line segment. In what ratio does a midpoint partition a segment?
::线段的中点是线段中间的点。中点是线段中间的点。中点分区是哪个比例?

1:1, because the segments connecting the midpoint to each endpoint will be the same length.
::1:1,因为中点与每个终点的连接段长度相同。

Example 4
::例4

Consider $\begin{aligned} \bar{B A} \end{aligned}$ with $\begin{aligned} B = (4, 1) \end{aligned}$ and $\begin{aligned} A = (10, 2) \end{aligned}$ . $\begin{aligned} P \end{aligned}$ partitions the segment in a ratio of 2:3. Find the coordinates of point $\begin{aligned} P \end{aligned}$ . How and why is this answer different from the answer to example under Finding the Coordinates of a Point?
::以 BA 和 B= (4, 1) 和 A = (10, 2) 来考虑 BA 和 BA 和 BA 和 A = (10, 2) 。 P 分区的比例为 2 : 3. 找到点P 的坐标。这个答案与查找点坐标下的答案有何不同?

$\begin{aligned} (x_{1}, y_{1}) = (4, 1) \end{aligned}$ and $\begin{aligned} (x_{2}, y_{2}) = (10, 2) \end{aligned}$ . $\begin{aligned} m = 2 \end{aligned}$ and $\begin{aligned} n = 3 \end{aligned}$ .
:x1,y1)=(4,1)和(x2,y2)=(10,2),m=2和n=3。

$\begin{aligned} P = (\frac{m x_{2} + n x_{1}}{m + n}, \frac{m y_{2} + n y_{1}}{m + n}) & = (\frac{2 \cdot 10 + 3 \cdot 4}{2 + 3}, \frac{2 \cdot 2 + 3 \cdot 1}{2 + 3}) \\ = (6.4, 1.4) \end{aligned}$
::P= (mx2+nx1m+n,my2+ny1m+n) = (2}10+342+3;2×2+3×2+3×12+3) =(6.4,1.4)

This answer is different from the answer to the above example because in this case point $\begin{aligned} P \end{aligned}$ is partitioning the segment in a 2:3 ratio starting from point $\begin{aligned} B . \end{aligned}$ In the above example, you were starting from point $\begin{aligned} A . \end{aligned}$
::这个答案与上述例子的答案不同,因为在这种情况下,P点从B点开始,正以2:3的比例分割段段段段。在上述例子中,您是从A点开始的。

INTERACTIVE

Midpoint Formula

Move the red points to find different midpoints on the graph.
::移动红点以在图形中找到不同的中点。

CK-12 PLIX: Midpoints and Segment Bisectors
::CK-12 PLIX:中点和分段

Summary

A line segment is a finite "part" of a line . Line segments have two endpoints.
::线条段是线条中有限的“部分”。线条段有两个端点。

Two figures are similar if they have the same shape, but not necessarily the same size.
::两个数字相似,如果形状相同,但不一定大小相同。

The midpoint formula $\begin{aligned} = (\frac{x_{2} + x_{1}}{2}, \frac{y_{2} + y_{1}}{2}) \end{aligned}$
::中点公式 = (x2+x12,y2+y12)

A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the side opposite the vertex.
::三角形的中位数是指将三角形的顶点与顶点对面侧的中点连接在一起的线段。

Review
::审查审查审查审查

Find the midpoint of each of the following segments defined by the given endpoints.
::查找由给定端点定义的以下各段的中点。

1. $\begin{aligned} (2, 6) \end{aligned}$ and $\begin{aligned} (- 4, 8) \end{aligned}$
::1. (2,6)和(-4,8)

2. $\begin{aligned} (1, 9) \end{aligned}$ and $\begin{aligned} (- 2, 5) \end{aligned}$
::2.(1,9)和(-2,5)

3. $\begin{aligned} (11, 24) \end{aligned}$ and $\begin{aligned} (8, 12) \end{aligned}$
::3. (11,24)和(8,12)

4. $\begin{aligned} (1, 3) \end{aligned}$ is the midpoint of $\begin{aligned} \bar{A B} \end{aligned}$ with $\begin{aligned} A = (- 2, 1) \end{aligned}$ . Find the coordinates of $\begin{aligned} B \end{aligned}$ .
::4. (1,3) 是A=(-2,1)的AB ' 中点。

5. $\begin{aligned} (2, 4) \end{aligned}$ is the midpoint of $\begin{aligned} \bar{C D} \end{aligned}$ with $\begin{aligned} C = (- 5, 9) \end{aligned}$ . Find the coordinates of $\begin{aligned} D \end{aligned}$ .
::5. (2,4)是CD'm与C=(-5,9)的中点。

6. $\begin{aligned} (4, 23) \end{aligned}$ is the midpoint of $\begin{aligned} \bar{E F} \end{aligned}$ with $\begin{aligned} E = (7, 11) \end{aligned}$ . Find the coordinates of $\begin{aligned} F \end{aligned}$ .
::6. (4,23)是E=(7,11)的EF的中点,找到F的坐标。

Consider $\begin{aligned} A = (- 9, 4) \end{aligned}$ and $\begin{aligned} B = (11, 17) \end{aligned}$ .
::考虑A=(-9,4)和B=(11,17)。

7. Point $\begin{aligned} P_{1} \end{aligned}$ partitions the segment from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} B \end{aligned}$ in a 3:5 ratio. Find the coordinates of point $\begin{aligned} P_{1} \end{aligned}$ .
::7. 点P1按3:5的比例将段段从A到B分割。查找点P1的坐标。

8. Point $\begin{aligned} P_{2} \end{aligned}$ partitions the segment from $\begin{aligned} B \end{aligned}$ to $\begin{aligned} A \end{aligned}$ in a 3:5 ratio. Find the coordinates of point $\begin{aligned} P_{2} \end{aligned}$ .
::8. 点P2分割区段从B到A的比例为3:5。查找点P2的坐标。

9. Why are the answers to 7 and 8 different?
::9. 为什么对7和8的答案不同?

10. Find the length of $\begin{aligned} A P_{1} \end{aligned}$ and $\begin{aligned} P_{2} B \end{aligned}$ . Why should these lengths be the same?
::10. 找出AP1和P2B的长度。为什么这些长度应该相同?

Consider $\begin{aligned} A = (- 6, - 1) \end{aligned}$ and $\begin{aligned} B = (4, 8) \end{aligned}$ . Use this to answer questions 11 & 12.
::考虑A=(-6)-1和B=(4,8),用这个回答问题11和12。

11. Point $\begin{aligned} P_{3} \end{aligned}$ partitions the segment from $\begin{aligned} A \end{aligned}$ to $\begin{aligned} B \end{aligned}$ in a 1:2 ratio. Find the coordinates of point $\begin{aligned} P_{3} \end{aligned}$ .
::11. P3点将段段从A到B按1:2的比例分隔。找出P3点的坐标。

12. Point $\begin{aligned} P_{4} \end{aligned}$ partitions the segment from $\begin{aligned} B \end{aligned}$ to $\begin{aligned} A \end{aligned}$ in a 4:5 ratio. Find the coordinates of point $\begin{aligned} P_{4} \end{aligned}$ .
::12. P4点将分段从B到A按4:5的比例分隔。找出P4点的坐标。

13. Point $\begin{aligned} P = (1, 2) \end{aligned}$ partitions the segment from $\begin{aligned} E = (9, 6) \end{aligned}$ to $\begin{aligned} F \end{aligned}$ in a 2:5 ratio. Find the coordinates of point $\begin{aligned} F \end{aligned}$ .
::13. Ppo点=(1,2)将E=(9,6)至F的段段分割成2:5的比例。查找F点的坐标。

14. Point $\begin{aligned} P = (- 6, - 4) \end{aligned}$ partitions the segment from $\begin{aligned} G = (- 4, 6) \end{aligned}$ to $\begin{aligned} H \end{aligned}$ in a 5:3 ratio. Find the coordinates of point $\begin{aligned} H \end{aligned}$ .
::14. P点=(-6)-(4)分区,从G=(-4)6到H段,比例为5:3。找出H点的坐标。

15. Point $\begin{aligned} P = (6, 8) \end{aligned}$ partitions the segment from $\begin{aligned} I = (- 2, 1) \end{aligned}$ to $\begin{aligned} J \end{aligned}$ in a 6:7 ratio. Find the coordinates of point $\begin{aligned} J \end{aligned}$ .
::15. P点=(6,8) 比例为 6: 7, 从 I = (-2,1) 到 J 段的分区。查找 J点的坐标。

16. A triangle is defined by the points $\begin{aligned} (5, 6) \end{aligned}$ , $\begin{aligned} (9, 17) \end{aligned}$ , and $\begin{aligned} (- 2, 1) \end{aligned}$ . Find the coordinates of the centroid of the triangle.
::16. 三角形由点(5,6,6,9,17)和点(-2,2)界定。

17. Prove that the midpoint, M, of the hypotenuse of a right triangle is equidistant from the three vertices.
::17. 证明右三角形下方的中点M与三个顶点的距离相等。

18. Square ABCD has an area of 800. E is the midpoint of AC and F is the midpoint of AB. What is the area of the trapezoid BCEF? Justify your answer.
::18. ABCD广场面积为800。 E是AC的中点,F是AB的中点。 CBEF 陷阱区域是哪里?请说明答案。

19. Using the following diagram, can you determine if the midpoint of AB falls on the edge of one of the rectangles? Justify your answer. Does the point C fall on the line that passes through AB? Justify your answer.
::19. 使用下图,您能否确定 AB 中点是否落在矩形之一的边缘? 请说明答案。 C 点是否落在通过 AB 的线上? 请说明答案。

20. In the diagram below, you are given that X is on the point AD and divides AD in a ratio of 2:1. Y is on the line BF which divides BF in a ratio of 2:1. Finally Z is on the line CE which divides CE in a ratio of 2:1. Find the coordinates of X, Y, and Z. What conclusions can you draw? Explain.
::20. 在下图中,您被告知,X在点AD上,将AD除以2:1。Y在线BF上,BF在比例2:1。最后,Z在线CE上,CE在比例2:1。找到X、Y和Z的坐标。你能得出什么结论?解释。

Review (Answers)
::审查(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Proving Triangle Similarity ::证明三角形相似性

Finding Length and Height ::查找长度和高度

Finding the Coordinates of a Point ::查找点的坐标

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

CK-12 PLIX: Midpoints and Segment Bisectors ::CK-12 PLIX:中点和分段

Review ::审查审查审查审查

Review (Answers) ::审查(答复)