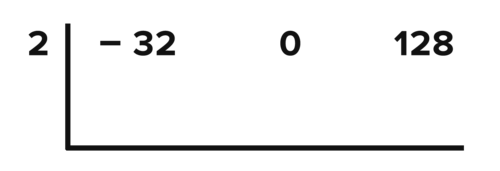Section: 合成司 | 1.5 合成司-interactive

Section outline

Learning Objectives
::学习目标

Understand the relationship between synthetic division and long division of polynomials.
::了解合成分裂与长期多民族分裂之间的关系。

Know and apply the Remainder Theorem
::了解并应用残余定理

Divide using synthetic division.
::使用合成分除法进行除法。

Introduction: Average Velocity
::导言:平均速率

The height of skydivers above can be modeled using a polynomial.
::上面的天空潜水器的高度可以用一个多面形模型来模拟。

One of the challenges mathematicians face is finding instantaneous rates like instantaneous velocity. Instantaneous velocity is the velocity of an object at a specific moment in time. Many of the devices used to determine instantaneous velocity use estimates based on average velocity. Average velocity describes the distance traveled by an object over a period of time and can be calculated, in this case, using the following formula :
::数学家面临的挑战之一是找到像瞬时速度这样的瞬时速率。瞬时速度是特定时间一个物体的速度。许多用于根据平均速度确定瞬时速度使用估计值的设备。平均速度描述一个物体在一段时期内所穿行的距离,在此情况下,可以使用以下公式计算:

$\begin{align*}\text{average velocity} = \frac{\text{distance}}{\text{time}}=~\frac{\text{ending position} - \text{starting height}}{\text{ending time} - \text{starting time}}\end{align*}$
::平均速度=远距离时间=结束位置 - 开始高度时间 - 开始时间

Example
::示例示例示例示例

A skydiver jumps from a plane 10,000 feet above ground level. The height of the skydiver above the ground, in feet, can be modeled using the polynomial $\begin{align*}-32t^2 + 10,000\end{align*}$ in the absence of friction. Use the interactive below to calculate the average velocity over various intervals and to make observations about the relationship between average velocity and instantaneous velocity.
::从地面上10 000英尺的平面上跳出一个天空潜水器。地面上天空潜水器的高度,在没有摩擦的情况下,可以用多边-32t2+10 000来模拟。使用下面的交互作用来计算不同间隔的平均速度,并对平均速度和瞬时速度之间的关系进行观察。

Discussion Questions :
::讨论问题:

Why are these velocities different, and what does it tell you?
::为什么这些速度不同? 它告诉你什么?

Use the interactive to estimate the instantaneous velocity at 5 seconds. Explain what methods you used to get your answer.
::使用交互程序来估计 5 秒的瞬时速度。请解释您使用什么方法来获得答案。

Suppose you wanted to find the average velocity from 2 to $\begin{align*}x\end{align*}$ seconds, how could you go about doing this?
::假设你想找到2到x秒的平均速度你怎么能这么做呢?

Activity 1: Understanding Synthetic Division
::活动1:理解合成司

Example
::示例示例示例示例

Use synthetic division to solve $\begin{align*}(x^4 + 4x^2 + 5x - 5) \div (x - 3)\end{align*}$
::使用合成分解解( x4+4x2+5x-5) (x-3)

When a polynomial is divided by a first degree polynomial with a leading coefficient of 1, there are patterns t o take advantage of. Examine the example below and state any patterns that you observe.
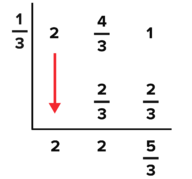
::当多面体除以一级多面体, 且主要系数为 1 时, 有利用模式。请看看下面的示例, 并描述您所观察到的任何模式。

Synthetic division is an algorithm that takes advantage of these patterns. Use the interactive below to explore how it works.
::合成分裂是一种利用这些模式的算法。使用下面的互动来探索它是如何运作的。

The image below displays the steps of each process. Use your knowledge of both methods and the interactive below to explore the connections between them.
::下面的图像显示每个过程的步骤。使用您对方法的了解和下面的互动来探索它们之间的联系。

Long Division VS Synthetic Division
::VS 长长司 VS 合成司

Activity 2: Average Velocity Continued
::活动2:平均速度持续

Now that you know how to use synthetic division, it's time to find the average velocity from 2 to $\begin{align*}x\end{align*}$ seconds from the introduction. A ssume that $\begin{align*}x\end{align*}$ is a value greater than 2. Recall that a skydiver jumps from a plane 10,000 feet above ground level. The height of the skydiver above the ground, in feet, can be modeled using the polynomial $\begin{align*}-32t^2 + 10,000\end{align*}$ in the absence of friction.
::现在你知道如何使用合成分解, 现在是时候从引言处找到2到x秒的平均速度了。假设x是一个大于2的值。提醒大家注意, 平面上从1万英尺高的平面上跳下天空潜水器。在没有摩擦的情况下, 地面上天空潜水器的高度, 以脚为单位, 可以用多位数 - 32t2+10 000 模型模拟。

To find the average velocity at $\begin{align*}x\end{align*}$ seconds, find the distance traveled and the time. To find the time, s ubtract the starting time from the ending time. In this case, the ending time is $\begin{align*}x,\end{align*}$ and the starting time is 2, so the overall time will be $\begin{align*}x - 2.\end{align*}$ To find the distance, subtract the starting height from the ending height. The ending height is $\begin{align*}(-32(x)^2 + 10,000)\end{align*}$ and the starting height is $\begin{align*}(-32(2)^2 + 10,000).\end{align*}$
::要在 x 秒找到平均速度, 请找到行走的距离和时间。要找到时间, 请从结束时间中减去开始时间。在这种情况下, 结束时间为 x, 开始时间为 2, 所以总时间为 x-2 。要找到距离, 请从结束高度中减去起步高度。结束高度为 (-32( x) 2+ 10,000) , 起始高度为 (-32 (2)+ 10,000) 。

$\begin{align*}&(-32(x)^2 + 10,000) - (-32(2)^2 + 10,000) \\ &-32x^2 + 10,000 + 32(2)^2 - 10,000 \\ &-32x^2 + 32(2)^2 \\ &-32x^2 + 32(4) \\ &-32x^2 + 128\end{align*}$
:-32(x)2+10 000)-(-32(2)2+10 000)-32x2+10 000)-32x2+10 000+32(2)2-10 000-32x2+32(2)2-32x2+322+32(4)-32x2+128)

Now that you know the distance traveled toward the ground is $\begin{align*}-32x^2 + 128\end{align*}$ feet, and the time over that distance is $\begin{align*}x-2\end{align*}$ seconds, you can divide the distance by the time to find the velocity.
::现在你知道通往地面的距离是 - 32x2+128英尺, 而距离的长度是 x-2 秒, 您可以在时间上分隔距离以找到速度。

$\begin{align*}\frac{-32x^2 + 128}{x-2}\end{align*}$
::- 32x2+128x-2

Since the divisor is a first-degree polynomial with a leading coefficient of 1, you can use synthetic division. Write the opposite of the constant of the divisor in the divisor position. T he coefficients of the dividend should be written in the dividend position. Remember that the dividend $\begin{align*}-32x^2 + 128\end{align*}$ is missing an $\begin{align*}x\text{-}\end{align*}$ term so it must be included it as $\begin{align*}0x.\end{align*}$
::divisor 是一度多面性, 以1为主要系数, 您可以使用合成分法。与 divisor 位置上的 divisor 常数相反的写。股息的系数应该写在股息位置上。记住, 股息 - 32x2+128 缺少一个 x 期, 所以它必须包含为 0x 。

P erform the synthetic division algorithm as follows:
::执行下列合成分区算法:

Answer: The average velocity of the skydiver over the interval 2 to $\begin{align*}x\end{align*}$ seconds is modeled by the polynomial $\begin{align*}-32x - 64.\end{align*}$ Additionally, since the remainder is zero, you know that $\begin{align*}x - 2\end{align*}$ is a factor of $\begin{align*}-32x^2 + 128.\end{align*}$
::回答:2至x秒间距的天空潜水器平均速度由多角度-32x-64模拟。此外,由于其余部分为零,你知道 x-2 是- 32x2+128的系数。

Activity 3: The Remainder Theorem
::活动3:残余定理

Recall from that you can rewrite the quotient as the product of the divisor and the dividend plus the remainder.
::回想一下,你可以改写商数,将商数改写为分数和股息加上剩余部分的产物。

See how $\begin{align*}(x^2 + 3x + 6) \div (x+1) = x + 2 + \tfrac{4}{x + 1}\end{align*}$ in the example above. S ubstituting -1 into the polynomial function $\begin{align*}f(x) = x^2 + 3x + 6\end{align*}$ will produce the following:
::参见上述示例中的 (x2+3x+6) (x+1) =x+2+4x+1 。将 -1 替换为多边函数 f(x) =x2+3x+6 将产生以下结果 :

$\begin{align*}f(-1) &= (-1)^2 + 3(-1) + 6 \\ &= 1 - 3 + 6 \\ &= 4\end{align*}$
::f(-1)=(-1)2+3(-1)+6=1-3+6=4

Is it a coincidence that the remainder of $\begin{align*}(x^2 + 3x + 6) \div (x+1)\end{align*}$ is equal to $\begin{align*}f(-1)\end{align*}$ ? Use the interactive below to explore this relationship.
:x2+3x+6) {(x+1) 的剩余部分等于 f(-1) 是巧合吗? 使用下面的交互方式来探索这种关系。

This relationship is called the remainder theorem.
::这种关系被称为其余的定理。

Remainder Theorem
::保留定理

If a polynomial of degree $\begin{align*}n > 0\end{align*}$ is divided by $\begin{align*}x - c,\end{align*}$ then the remainder $\begin{align*}R\end{align*}$ is a constant equal to the value of the polynomial when $\begin{align*}c\end{align*}$ is substituted for $\begin{align*}x.\end{align*}$ That is $\begin{align*}f(c) = R.\end{align*}$

T his relationship can be used to quickly find outputs to polynomial functions.
::这种关系可用于迅速找到多功能的输出。

Example
::示例示例示例示例

Use synthetic division to find the $\begin{align*}f(4)\end{align*}$ if $\begin{align*}f(x) = 3x^3 - x^2 - 6x - 27.\end{align*}$
::如果f(x)=3x3-x2-6x-27,则使用合成项来查找 f(4) f(x)=3x3-x2-6x-27。

As polynomials get more complex, synthetic division will become a time saver.
::合成分裂会成为节省时间的工具。

Extension: Expanding Synthetic Division
::扩展:扩大合成科

You can extend the use of synthetic division from divisors of the form $\begin{align*}x - c,\end{align*}$ to divisors of the form $\begin{align*}ax - c\end{align*}$ by dividing every term in both the divisor and dividend by $\begin{align*}a.\end{align*}$ This division will result in an equivalent division problem of the form $\begin{align*}x - c.\end{align*}$ This idea is similar to dividing decimals. To divide 7.32 by 1.2, move the decimal one place in both the divisor and the dividend to produce an equivalent division problem with no decimal in the divisor.
::您可以将合成分数从表x-c的分数扩大到表A-c的分数,将表A-c的分数除以a。这一分数将造成表x-c的相等分数问题。这个想法与小数分数相似。将7.32除以1.2,将小数位数移到分数和股分中的一个位数,从而产生相等的分数问题,小数点数没有小数点。

$\begin{align*}\frac{7.32\times10}{1.2\times10}=\frac{73.2}{12}\end{align*}$ Example
::7.32x101.2x10=73.212

Divide $\begin{align*}(6x^2 +4x+3) \div (3x-1)\end{align*}$
::除法( 6x2+4x+3) ( 3x- 1)

To get $\begin{align*}3x-1\end{align*}$ in the form $\begin{align*}x - c,\end{align*}$ divide $\begin{align*}3x-1\end{align*}$ by 3. Any change made to the divisor must also be made to the dividend to keep the division equivalent. Therefore , you must divide both the numerator and denominator by 3.
::要获得表x-c中的 3x-1, 将 3x-1 除以 3. 对分数的任何更改也必须对分数进行, 才能保持等数。因此, 您必须将分子和分母除以 3 。

$\begin{align*}\frac{(6x^2 +4x+3)\div3}{(3x-1)\div3}&=\frac{(6\div3)x^2 + (4\div3)x + (3\div3)}{(3\div3)x - (1\div3)}\\\\ &=\frac{2x^2 + \frac{4}{3}x + 1}{1x - \frac{1}{3}}\\\\ &= \left( 2x^2 + \frac{4}{3}x + 1 \right) \div \left( 1x - \frac{1}{3} \right)\end{align*}$
:6x2+4x+3)3(3x-1)3=(63)x2+(43)x+(33)xx(33)x-(13)x-(13)=2x2+43x+11x-13=(2x2+43x+1)(1x-13)

The expression $\begin{align*}\left( 2x^2 + \frac{4}{3}x + 1 \right) \div \left( x - \frac{1}{3} \right)\end{align*}$ will result in the same answer as the expression $\begin{align*}(6x^2 +4x+3) \div (3x-1)\end{align*}$ because they are equivalent. U se synthetic division to divide the equivalent expression since $\begin{align*}x - \frac{1}{3}\end{align*}$ is of the form $\begin{align*}x-c\end{align*}$ with $\begin{align*}c=\frac{1}{3}.\end{align*}$ The synthetic division will play out as follows:
::表达式 (2x2+43x+1) (x- 13) 将产生与表达式( 6x2+4x+3) ( 3x- 1) 相同的答案, 因为它们是等效的。使用合成分隔法来分隔等效表达式, 因为 x- 13 是以 c=13 的 x- c 形式。合成分割法将发挥以下作用 :

Answer: $\begin{align*}x+2+\frac{\frac{5}{3}}{x-\frac{1}{3}}\end{align*}$
::答复:x+2+53x-13

Use long division to verify your answer. Since you are dividing by a different denominator, you will get a different remainder. Are they equivalent? Prove your answer.
::使用长的分区来校验您的回答。由于您被不同的分母分隔, 您将得到不同的剩余部分。它们是否相等 ? 证明您的回答。

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要

You can divide two polynomials using synthetic division if the divisor is a first-degree polynomial with a leading coefficient of 1.
::您可以使用合成分裂法来分割两个多面体,如果断层是一级多面体,主要系数为1。

When setting up a synthetic division problem with a dividend that is missing a term, add a zero in the place of the missing term.
::当用缺少一个术语的红利来建立合成分裂问题时,在缺失术语的位置上加上零。

When setting up a synthetic division problem remember to use the opposite of the $\begin{align*}c\end{align*}$ term in the divisor, $\begin{align*}x−c.\end{align*}$

::当设置合成分解问题时, 记得使用与 disvisor, x- c 中的 c 词相反的词。

The Remainder Theorem says that if a polynomial of degree $\begin{align*}n\end{align*}$ is divided by $\begin{align*}x - c,\end{align*}$ then the remainder $\begin{align*}R\end{align*}$ is a constant equal to the value of the polynomial when $\begin{align*}c\end{align*}$ is substituted for $\begin{align*}x.\end{align*}$ That is $\begin{align*}f(c) = R.\end{align*}$
::遗迹论者表示,如果一多元度 n 除以 x - c, 那么其余的 R 是常数, 当 c 取代 x 时, 则等于该多数值。这是 f( c) = R 。

Section outline

Introduction: Average Velocity ::导言:平均速率

Activity 1: Understanding Synthetic Division ::活动1:理解合成司

Activity 2: Average Velocity Continued ::活动2:平均速度持续

Activity 3: The Remainder Theorem ::活动3:残余定理

Remainder Theorem ::保留定理

Extension: Expanding Synthetic Division ::扩展:扩大合成科

Wrap-Up: Review Questions ::总结:审查问题

Summary ::摘要

Introduction: Average Velocity
::导言:平均速率

Activity 1: Understanding Synthetic Division
::活动1:理解合成司

Activity 2: Average Velocity Continued
::活动2:平均速度持续

Activity 3: The Remainder Theorem
::活动3:残余定理

Remainder Theorem
::保留定理

Extension: Expanding Synthetic Division
::扩展:扩大合成科

Wrap-Up: Review Questions
::总结:审查问题

Summary
::摘要