节: 复数数 | 3.8 复杂数字-interactive

章节大纲

Lesson Objectives
::经验教训目标

Understand the characteristics and structure of complex numbers and plot them on the plane.
::了解复杂数字的特性和结构,在飞机上绘制。

State the complex number given a point on the complex plane .
::在复杂的平面上说明一个点的复杂数字。

by completing the square.
::通过完成广场。

Understand how complex roots of a quadratic are represented on the complex plane.
::了解复杂的平面上如何代表复杂的二次方根

Understand how rotating $\begin{align*}i\end{align*}$ about the complex plane is related to the powers of $\begin{align*}i.\end{align*}$
::了解如何旋转我关于复杂的平面与我的权力有关。

Simplify $\begin{align*}i\end{align*}$ to a given power.
::将 i 简化为给定权力。

Add , subtract, and multiply complex numbers.
::添加、减、乘复数。

Simplify expressions with complex numbers, and s olve problems involving complex conjugates.
::简化有复杂数字的表达方式,解决涉及复杂共产体的问题。

Introduction: Math Duels
::一. 导言:数学

T he quadratic formula used to solve any quadratic equation can be derived by completing the square. The next logical step is to develop a formula for solving cubic equations. Italian mathematician and professor at Bologna, Scipione del Ferro, developed a formula for cubic equations of the form $\begin{align*}𝑥^3=𝑎𝑥+𝑏x\end{align*}$ where $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are positive rational numbers. He shared his formula with his student Antonio Maria Fior, who kept the formula a secret. In 16th-century Italy, mathematicians challenged each other to mathematical duels. These duels were meant to garner acclaim and stake a claim to high ranking professional positions. A duel consisted of each mathematician giving the other a series of questions with the winner of the duel being decided based on accuracy and efficiency. Fior, who now believed himself to have the secret weapon to beating any mathematician, challenged mathematician Niccolo Tartaglia to a math duel. In the duel, Tartaglia was able to figure out the formula, and Fior lost.
::用于解决任何二次方程的二次公式可以通过完成方形来得出。下一个逻辑步骤是开发一个解决立方方方程的公式。意大利数学家和博洛尼亚教授、塞皮奥内德尔费罗(Scipione del Ferro)开发了一个公式方程式的立方方程x3=ax+bx, 其中a和b为正理性数字。他与学生Antonio Maria Fior分享了他的公式, 后者保留了公式的秘密。在16世纪的意大利, 数学家互相挑战数学决斗。这些决斗意在获得声名, 并争取获得高级专业职位。每个数学家在根据准确性和效率决定决决决决决决决决决决决决决决决决决决决决决胜者之间一系列问题。 Fior, 他现在相信自己拥有打数学家的秘密武器, 挑战数学家 Niccolo Tartagilia 向数学决斗。在决斗中, Tartagilia 能够提出公式, 以及 Fior 输输。

T he existing formula at the time of the duel did work in solving cubic equations, however, when the coefficients took on certain values, the formula would produce radicals with negative radicands. At this point in history, mathematicians assumed that any equations involving were unsolvable. Del Ferro's formula allowed mathematicians to solve these previously unsolvable equations. After this duel, Italian mathematicians embraced imaginary numbers as doing so provided them an advantage against other mathematicians in duels.
::决斗时的公式确实解决了立方方程式的问题,然而,当系数以某些数值计算时,公式会产生负弧度的基数。在历史的这一时刻,数学家认为任何涉及的公式都是无法解决的。德尔费罗的公式允许数学家解决这些以前无法解决的方程式。在这次决斗之后,意大利数学家将假想数字纳入其中,这样他们就能在决斗中与其他数学家相比获得优势。

To deal with a negative inside a radical, the letter $\begin{align*}i\end{align*}$ is used to represent $\begin{align*}\sqrt{-1}.\end{align*}$ The constant $\begin{align*}i\end{align*}$ marks the introduction to the imaginary numbers. An is a number that can be written as the product of a real number and the imaginary unit, $\begin{align*}i.\end{align*}$ Examples of imaginary numbers include $\begin{align*}3i, \:\tfrac{5}{6}i, \:17.2i, \:\pi i,\end{align*}$ and $\begin{align*}i\sqrt{2}.\end{align*}$ The imaginary numbers originated out of 16th-century Italian mathematics.
::为了处理激进分子内部的负数, i 字母用来代表 1. 常数i 标记虚构数字的引言。常数i 可以写成一个数字, 是真实数字和虚构单位的产物, 即虚构数字的例子包括 3, 56i, 17.2i, i 和 i2. 虚构数字来自十六世纪意大利数学。

Activity 1: Understanding Imaginary Numbers
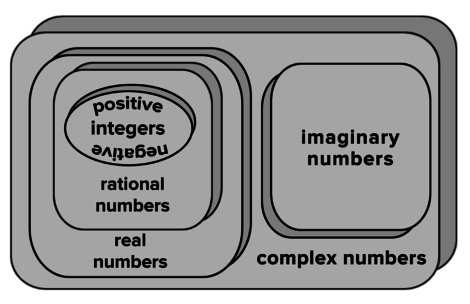
::活动1:了解想象数字

Imaginary numbers are a subset of complex numbers.
::想象数字是复杂数字的子集。

A complex number is a number that is the combination of a real number and an imaginary number. These numbers can be written in the form $\begin{align*}a + bi\end{align*}$ where $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are real numbers.
::复数是一个数字,它是一个实际数字和一个想象数字的组合。这些数字可以以a+B的形式写成,其中a和b为实际数字。

E xamples of complex numbers were introduced in the previous section, Rational and Irrational Roots, when a function had the x-intercepts $\begin{align*}150 ± 50i\sqrt{3}\end{align*}$ and $\begin{align*}-150 ± 50i\sqrt{3}.\end{align*}$ A complex number is a number that exists outside of the dimensions being used . The complex number $\begin{align*}3 - 4i\end{align*}$ has a real component of $\begin{align*}3\end{align*}$ and an imaginary component of $\begin{align*}\text{-}4.\end{align*}$ This can be represented on a complex plane, much like the point $\begin{align*}(3,\:\text{-}4)\end{align*}$ can be represented. The point for the number $\begin{align*}3 - 4i\end{align*}$ would line up with $\begin{align*}3\end{align*}$ on the real axis and -4 on the imaginary axis.
::在前一节“合理和不合理根”中引入了复杂数字的例子,当函数的 X 截取值为 150 50i3 和- 150 50i3. 时,复杂的数字是一个在所用维度以外存在的数字,3-4i 复合数的真构件为 3, 虚构成份为 - 4, 这可以在复杂的平面上表示, 与点( 3, 4) 大致相似。 3-4i 的点在实际轴上为 3, 虚构轴上为 4。

Use the interactive below to examine how the complex plane connects to the cartesian coordinate plane.
::使用下面的交互式平面来检查复杂的平面是如何连接到卡尔提斯坐标平面的

Example
::示例示例示例示例

Find the zeros of the function $\begin{align*}f(x) = x^2 - 4x + 5.\end{align*}$
::查找函数 f(x) =x2 - 4x+5 的零。

T he expression $\begin{align*}x^2 - 4x + 5\end{align*}$ cannot be factored; however, completing the square or can be used to solve the equation $\begin{align*}0 = x^2 - 4x + 5.\end{align*}$ Completing the square is used below.
::表达式 x2 - 4x+5 无法计算; 但是, 完成正方形或可用于解析等式 0=x2 - 4x+5 。以下使用完成正方形。

1. Divide all terms by the a-coefficient.
::1. 将所有术语除以系数。

Since the a-coefficient is 1, dividing each term but 1 will have no effect on the equation. Therefore, this step can be skipped.
::由于系数是1, 将每个任期除以1, 但一个任期对等式没有影响。因此, 此步骤可以跳过。

2. Move the constant term to the opposite side of the equation than the variables.
::2. 将常数移到方程的对面,而不是变量。

$\begin{align*}0 &= x^2 - 4x + 5\\ -5 & \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:-5\\ -5 &= x^2 - 4x\end{align*}$
::0=x2 - 4x+5-5 - 5 - 5 - 5=5=x2 - 4x

3. Add $\begin{align*}\left( \tfrac{b}{2}\right)^2\end{align*}$ to both sides of the equation.
::3. 将(b2)2添加到等式的两侧。

The b-coefficient is -4, so add $\begin{align*}{\left(\frac{-4}{2}\right)}^{2} = (-2)^2 = 4\end{align*}$ to both sides of the equation.
::b-系数为 4, 因此在方程的两侧加上 (-42)2=(-2)2=4。

$\begin{align*}-5 + 4 = x^2 - 4x + 4\\ -1 = x^2 -4x + 4\end{align*}$
::-5+4=x2-4x+4-1=x2-4x+4

4. Complete the square by factoring the equation.
::4. 通过计算方程来完成方形。

$\begin{align*}-1 = (x - 2)^2\end{align*}$
::-1=(x-2)2

5. Take the square root of both sides and solve.
::5. 解决双方的平方根。

$\begin{align*}\sqrt{-1} &= \sqrt{{(x-2)}^{2}}\\ ±\sqrt{-1} &= x-2\\ +2 \:\:\:\:\:\:\:&\:\:\:\:\:\:\:+ 2 \\ \hline 2 ± \sqrt{-1} &= x \\ \\ 2 ± i &= x\end{align*}$
::*1(x-2)221=x-2+2+221=x2i=x

Answer : $\begin{align*}x = 2 + i\end{align*}$ and $\begin{align*}x = 2 - i\end{align*}$
::答复:x=2+i和x=2-i

Use the interactive below to explore what these roots would look like on a graph in the complex plane.
::利用下面的交互性来探索这些根在复杂平面的图表上会是什么样子。

Activity 2: Powers of the Imaginary Number i
::活动2:想象数字i的力量

One way to think of the imaginary number $\begin{align*}i\end{align*}$ is as a rotation along the plane formed by the real axis and imaginary axis. Starting at 1, multiplying by $\begin{align*}i\end{align*}$ will result in a 90° rotation. Multiplying by $\begin{align*}i\end{align*}$ again will result in another 90° rotation, giving $\begin{align*}i^2 =-1.\end{align*}$ You can also prove this algebraically:
::想象数字 i 的一种方式是沿由真实轴和想象轴组成的平面旋转。从 1 开始乘以 i 将产生90 度的旋转。乘以 i 将再产生 90 度的旋转, 给 i2\\\\ 1 。您也可以证明这个代数 :

$\begin{align*}i^2&=i \cdot i\\ &=\sqrt{-1} \cdot \sqrt{-1}\\ &=\sqrt{-1}^2\\ &=-1\end{align*}$
::i2=ii_i_111121

U se the fact that $\begin{align*}i^2=-1\end{align*}$ to simplify $\begin{align*}i\end{align*}$ to higher powers.
::使用 i2 @% 1 来简化 i 到更高的权限。

Example 1
::例1

Simplify $\begin{align*}i^6\end{align*}$
::简化 i6

R ewrite $\begin{align*}i^6\end{align*}$ as $\begin{align*}i^2\times i^2\times i^2 \end{align*}$
::将i6重写为 i2xi2xi2

Now replace each $\begin{align*}i^2\end{align*}$ with -1 and simplify $\begin{align*}(-1)(-1)(-1)=-1\end{align*}$
::现在将每个 i2 替换为-1, 并简化 (-1) (-1) (-1) (-1) @% 1

Answer: $\begin{align*}i^6 = -1\end{align*}$
::答复:i6%1

You could also look at $\begin{align*}i^6\end{align*}$ as $\begin{align*}(i^4)(i^2) \text{ or } (1)(-1) = -1.\end{align*}$
::您也可以将 i6 视为 (i4)(i2) 或(1)(- 1) @% 1 。

Example 2
::例2

Simplify $\begin{align*}i^7\end{align*}$
::简化 i7

The expression $\begin{align*}i^7\end{align*}$ can be rewritten as $\begin{align*} i^2\times i^2\times i^2\times i.\end{align*}$
::表达式 i7 可以重写为 i2xi2xi2xi。

Now replace each $\begin{align*}i^2\end{align*}$ with -1 and simplify $\begin{align*}(-1)(-1)(-1)i = -i\end{align*}$
::现在将每个 i2 替换为-1, 并简化 (-1) (-1) (-1) (-1) (i) i @ i

Answer: $\begin{align*}i^7=-i\end{align*}$
::答复:i7i

Use the interactive below to explore this further.
::利用以下互动方式进一步探讨这一问题。

Discussion Question : Write a conjecture about the value of $\begin{align*}i^n.\end{align*}$
::讨论问题:撰写关于参与价值的猜测。

Activity 3: Operations with Complex Numbers
::活动3:复杂数字业务

Although complex numbers are not real numbers, they can still be added and subtracted. Remember that $\begin{align*}i=\sqrt{-1}.\end{align*}$ The sum of $\begin{align*}8i \end{align*}$ and $\begin{align*}3i\end{align*}$ can be thought of as the sum of $\begin{align*}8\sqrt{-1}\end{align*}$ and $\begin{align*}3\sqrt{-1}.\end{align*}$    The sum $\begin{align*}8\sqrt{-1}\end{align*}$ and $\begin{align*}3\sqrt{-1}\end{align*}$ will equal $\begin{align*}11\sqrt{-1} \text{ or } 11i\end{align*}$ the same way that $\begin{align*}8\sqrt{2}\end{align*}$ and $\begin{align*}3\sqrt{2}\end{align*}$ can be added to get $\begin{align*}11\sqrt{2}.\end{align*}$

::虽然复杂数字不是实际数字,但仍可以增减。记住i1。 8i和3i之和可被视作81和31之和。 81和31之和将等于111或11i, 与82和32之和可被加到112之和相同。

Example
::示例示例示例示例

Simplify $\begin{align*}(5 + 3i) + (6 - 8i)\end{align*}$
::简化( 5+3i)+( 6- 8i)

U se the commutative property to combine and add like terms:
::使用通量财产合并并添加类似术语:

$\begin{align*}(5 + 3i) + (6 - 8i) &=(5+6)+(3i-8i) \\&=11-5i\end{align*}$
:5+3i)+(6-8i)=(5+6)+(3i-8i)=11-5i

Answer: $\begin{align*}11-5i\end{align*}$
::答复:11-5i

Sums and Differences of Complex Numbers
::复杂数字的总和和差异

When adding (or subtracting) two or more complex numbers, the fastest method is to combine the real components to obtain the sum of the real numbers, and then separately add (or subtract) the coefficients of the imaginary numbers to obtain the sum of the imaginary terms.
::当添加(或减去)两个或两个以上复杂数字时,最快的方法是合并实际组成部分,以获得实际数字的总和,然后单独添加(或减去)假想数字的系数,以获得假想条件的总和。

$\begin{align*}(a + bi) + (c + di) = [a + c] + [b + d]i\end{align*}$
:a+b)+(c+di)=[a+c]+[b+d]i

Example
::示例示例示例示例

Combine : $\begin{align*}(3 - 2i) - (2 - 4i)\end{align*}$
::组合3-2i)-(2-4i)

Begin by d istributing the negative. From there , use the commutative property and combine like terms.
::开始分配负值。从那里,使用通货财产, 并结合类似条件。

$\begin{align*}(3-2i)-(2-4i)&=(3 - 2i) + (-2 +4i)\\ &=(3 - 2) + (-2i + 4i) \\ &=1+2i\end{align*}$
:3-2i)-(2-4i)=(3-2)-2(i)+(-2)+(-2+4i)=(3-2)-2)+(-2)+(-2)+(-2)+(-2i+4i)=1+2i

Answer : $\begin{align*}1+2i\end{align*}$
::答复:1+2i

Example
::示例示例示例示例

Simplify: $\begin{align*}(7+2i)(3-i)\end{align*}$
::简化( 7+2i)( 3- i)

To multiply complex numbers, use FOIL .
::乘以复杂数字,使用FOIL。

$\begin{align*}(7+2i)(3-i) &= 21-7i+6i-2i^2 \\ &= 21-i-2i^2 \\ & =21-i-2({\color{red}-1}) \\ & =21-i\:{\color{red}+2} \\ & =23-i\end{align*}$
:7+2i)(3-一)=21-7i+6i-2i2=21-i-2i2=21-2i-2i2=21-2i-2i-2(-2-1)=21-i+2=23-i)

Answer: $\begin{align*}23-i\end{align*}$
::答复:23-i

Use the interactive below to practice operations with complex numbers.
::使用下面的交互操作来操作数字复杂的操作。

Discussion Question : Will adding two complex numbers always result in a complex number? Will multiplying two complex numbers always result in a complex number?
::讨论问题:增加两个复杂数字是否总是导致一个复杂数字?两个复杂数字的乘数是否总是导致一个复杂数字?

Activity 4: Complex Conjugates
::活动4:复杂的共同点

Example
::示例示例示例示例

Multiply $\begin{align*}(5−4i) \cdot (5+4i)\end{align*}$
::乘数( 5-4i) ( 5+4i)

This form should remind you of the difference of squares from earlier in this section. The only difference between the two binomials here is that one has a positive second term, and the other a negative second term. The outer and inner terms cancel out when you combine them. Here that is done using the FOIL method:
::此窗体应该提醒您注意本节先前的方形差异。这里两个二进制之间的唯一区别是, 一个是正的第二任期, 另一个是负的第二任期。当您合并时, 外部和内词会取消。在此使用 FIL 方法完成 :

$\begin{align*}(5−4i)⋅(5+4i)\end{align*}$
:5-4i)(5+4i)

F: $\begin{align*}5⋅5=25\end{align*}$
::女:5 5=25

O: $\begin{align*}5⋅4i=20i\end{align*}$
::O:54i=20i

I: $\begin{align*}5⋅-4i=-20i\end{align*}$
::一: 5420i

L: $\begin{align*}-4i⋅4i=-16i^2\end{align*}$
::L: - 4i4i16i2

$\begin{align*}&= 25+(20i−20i)−16i^2\\ &=25−16i^2\end{align*}$
::=25+(20i-20i)-16i2=25-16i2

At this point, you can see the difference of squares, because 25 is a perfect square, and so is $\begin{align*}16i^2.\end{align*}$    Since this is a complex number, something interesting happens. Remember that $\begin{align*}i^2=-1:\end{align*}$
::在这一点上,你可以看到方形的差别, 因为25是一个完美的方形, 16i2也是一样。由于这是一个复杂的数字, 有趣的事情会发生。记住 i2\\\ 1:

$\begin{align*}&=25−16i^2\\ &=25−16(-1)\\ &=41\end{align*}$
::=25-16i2=25-16(-1)=41

Answer : 41
::答复:41

The factors $\begin{align*}(5−4i)\end{align*}$ and $\begin{align*}(5+4i)\end{align*}$ are complex conjugates. Complex conjugates are binomial complex numbers that differ only in the sign of the imaginary term, such as $\begin{align*}(3+2i)\end{align*}$ and $\begin{align*}(3-2i).\end{align*}$ Any time you multiply two complex numbers that differ only in the sign on the imaginary term, you will end up with a single real number. T his property can be used to rationalize complex fractions.
::因素( 5-4i) 和( 5+4i) 是复杂的共产体。复杂的共产体是二进制的复杂数字, 仅在假想术语的符号上有所不同, 如( 3+2i) 和( 3-2i) 。每当您乘以两个复杂数字, 仅在假想术语的符号上有所不同, 你最终会有一个单一的真数。此属性可以用来使复杂分数合理化。

Example
::示例示例示例示例

Simplify $\begin{align*}\frac{3+2i}{4−3i}\end{align*}$
::简化 3+2i4- 3i

To simplify two divided complex numbers, you need to get the imaginary number out of the denominator. To do that, just multiply the numerator and denominator of the expression by the conjugate of its denominator, since a complex number and its conjugate will simplify to a single real number:
::要简化两个分隔的复杂数字, 您需要从分母中获取想象中的数字。要做到这一点, 只需将表达的数和分母乘以其分母的组合, 因为一个复杂数字及其组合将简化成一个单一的实际数字 :

$\begin{align*}\hphantom{= \_} \frac{3+2i}{4-3i} \cdot \frac{4+3i}{4+3i} & =\frac{(3+2i)(4+3i)}{16-9i^2}\\ \ \\ &= \frac{12+17i+6i^2}{16-9i^2}\\ \ \\ &= \frac{12+17i+6(-1)}{16-9(-1)}\\ \ \\ &= \frac{6+17i}{25}\\\end{align*}$
::3+2i4-3i4+3i4+3i4+3i=(3+2i)(4+3i)16-9i2=12+17i+6i2-16-9i2=12+17i+6(-1)16-9(-1)=6+17i25

Answer : $\begin{align*}\frac{6+17i}{25}\\\end{align*}$
::答复:6+17i25

Discussion Question : What is the conjugate of 8?
::讨论问题:什么是8的结合?

Wrap-Up: Review Questions
::总结:审查问题

Use the video below to review the topics discussed above
::利用下面的视频来审查上文讨论的专题

Extension: Imaginary Zeros
::扩展名: 想象零

Use the interactive below to connect imaginary zeros to the fundamental theorem of algebra.
::使用下面的交互作用将想象中的零与代数的基本理论连接起来。

Summary
::摘要

The letter $\begin{align*}i\end{align*}$ is used to represent the imaginary number $\begin{align*}\sqrt{-1}.\end{align*}$
::i 用于代表假想编号 #% 1 。

A complex number is in the form $\begin{align*}a+bi\end{align*}$ where $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ are real numbers.
::复数以 a+B 格式表示,其中a和b为实际数字。

Use the fact that $\begin{align*}i^2=-1\end{align*}$ to simplify $\begin{align*}i\end{align*}$ to different powers.
::使用 i2 @% 1 来将i 简化为不同的权力。

When adding and subtracting complex numbers combine the $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ and combine $\begin{align*}b\end{align*}$ and $\begin{align*}d:\end{align*}$ $\begin{align*}(a+bi)+(c+di)=[a+c]+[b+d]i\end{align*}$
::当加和减去复合数字时,将a和b合并,并合并b和da+bi)+(c+di)=[a+c]+[b+d]i

Complex conjugates are binomial numbers that differ only in the sign of the imaginary term, for example, $\begin{align*}(a+bi)\end{align*}$ and $\begin{align*}(a-bi)\end{align*}$ are complex conjugates.
::复杂的共同点是二元制数字,只有想象中的术语的符号不同,例如(a+bi)和(a-bi)是复杂的共同点。

When you multiply complex conjugates you will end up with a real number.
::当你乘以复杂的共产物时,你最终会有一个真实的数字。

章节大纲

Introduction: Math Duels ::一. 导言:数学

Activity 1: Understanding Imaginary Numbers ::活动1:了解想象数字

Activity 2: Powers of the Imaginary Number i ::活动2:想象数字i的力量

Activity 3: Operations with Complex Numbers ::活动3:复杂数字业务

Sums and Differences of Complex Numbers ::复杂数字的总和和差异

Activity 4: Complex Conjugates ::活动4:复杂的共同点

Wrap-Up: Review Questions ::总结:审查问题

Extension: Imaginary Zeros ::扩展名: 想象零

Summary ::摘要

Introduction: Math Duels
::一. 导言:数学

Activity 1: Understanding Imaginary Numbers
::活动1:了解想象数字

Activity 2: Powers of the Imaginary Number i
::活动2:想象数字i的力量

Activity 3: Operations with Complex Numbers
::活动3:复杂数字业务

Sums and Differences of Complex Numbers
::复杂数字的总和和差异

Activity 4: Complex Conjugates
::活动4:复杂的共同点

Wrap-Up: Review Questions
::总结:审查问题

Extension: Imaginary Zeros
::扩展名: 想象零

Summary
::摘要