Section outline

  • Lesson Objectives
    ::经验教训目标

    • Use the mean and to fit it to a normal distribution and to estimate population percentages.
      ::使用平均值,使其适应正常分布和估计人口百分比。
    • Use calculators, spreadsheets, and tables to estimate areas under the normal curve .
      ::使用计算器、电子表格和表格来估计正常曲线下的区域。

    Introduction: The World's Tallest Trees
    ::一. 导言:世界最高树

    lesson content
    An image of a redwood tree

    In the previous section, you saw how the could be used to describe the proportion of data that falls between z scores for normally distributed data. Use the example below to refresh your memory.
    ::在上一节中,您看到如何使用这些数据来描述通常分布的数据在z分之间的数据比例。使用下面的示例来更新您的记忆。

    Jeff is a scientist who plans to study the distribution of the heights of California redwood trees. Use the interactive below to take height measurements. The results will be displayed in a frequency histogram using intervals determined by the z scores of the data. Use the interactive below to take 5,000 measurements and answer the following questions.
    ::Jeff是一位科学家,他计划研究加利福尼亚红木树高高的分布。 使用下面的交互测量来测量高度。 其结果将以频率直方图显示, 使用由数据z分决定的间隔。 使用下面的交互测量来进行 5,000 度测量并回答下列问题 。

    INTERACTIVE
    The World's Tallest Trees
    minimize icon

    Use the interactive to take 5,000 normally distributed redwood tree height measurements. 
    ::使用互动方式进行正常分布的5 000次红木树高度测量。

    • Take additional measurements by clicking +100 or +1000.
      ::点击 +100 或 +1000 进行额外的测量 。
    • Use the first checkbox to show/hide the empirical rule proportions 68-95-99.7.
      ::使用第一个复选框显示/隐藏68-95-99.7比例的经验规则。
    • Use the second checkbox to show/hide the height intervals corresponding with the z-scores along the x-axis.
      ::使用第二个复选框来显示/隐藏与 X 轴沿线的 z 分数相应的高度间隔。
    Your device seems to be offline.
    Please check your internet connection and try again.
    +
    Do you want to reset the PLIX?
    Yes
    No

    Discussion Question: Approximately what percentage of Redwood tree height falls between 0.5 standard deviations below the mean and 0.5 standard deviations above the mean?
    ::讨论问题:红木树高在0.5标准偏差低于平均值和0.5标准偏差高于平均值之间的百分比约为多少?

    Activity 1: The Standard Normal Distribution Table
    ::活动1:标准正常分配表

    The area under the curve approximates the proportion of data that will fall within a range of z scores. Using the following normal distribution function, we can calculate the at any given interval . The entire area is 1 because the frequency distribution represents 100% of the data value (the whole set). The area under the curve will represent the proportion of the entire area as well as the proportion of the dataset.
    ::曲线下的区域接近属于z分范围内的数据比例。使用以下的正常分布函数,我们可以在任何给定的间隔内计算数据。整个区域为1,因为频率分布为数据值的100%(整个数据集)。曲线下的区域将代表整个区域的比例以及数据集的比例。

    INTERACTIVE
    The Standard Normal Distribution
    minimize icon
    • Adjust the two sliders on the x-axis to select an interval and find the area under the standard normal distribution curve. 
      ::调整 X 轴上的两个幻灯片以选择间隔,并在标准正常分布曲线下找到区域。
    • The area is rounded to 4 decimal places.
      ::区域四舍五入至小数点后四位数。
    Your device seems to be offline.
    Please check your internet connection and try again.
    +
    Do you want to reset the PLIX?
    Yes
    No

    The area values in the interactive above come from the normal distribution function below.
    ::上方交互式区域值来自下面的正常分配函数。

    lesson content
    The Normal Distribution Function
    • 𝝁 is the mean
      ::~ 是平均值 ~
    • 𝜎 is the standard deviation
      ::XIII 是标准偏差
    • 𝜋 ≈ 3.1415…
    • e ≈ 2.7182...
      ::e 2.7182...

    To find the of this function, we would need to know some calculus. To get around the need for calculus, many statisticians use a table of values. . You can also access the table under related content.
    ::要找到此函数,我们需要知道一些微积分。要绕过微积分的需要,许多统计人员使用一个数值表。您也可以在相关内容下访问该表。

    The values in this table represent the area under the curve to the left of the given z score. For example, a z score of 1.15 will have a table value of 0.8749. Approximately 87.49% of the values in the population dataset should fall below a z score of 1.15. Keep in mind that each z score can be related to specific values in a dataset.
    ::本表中的数值代表给定z分左侧曲线下的区域。例如,z分为1.15,表值为0.8749,人口数据集中值的大约87.49%应低于z分为1.15。请注意,每个z分可能与数据集中的具体值有关。

    lesson content
    Normally distributed data with a z score at 1.15. The area below the z score is displayed.

    The z scores run both vertically and horizontally along the outside of the table. The possible ones place and tenths place values of the z score run along the left of the table vertically. The possible hundredths place values of the z score run along the top of the table horizontally. When you match up a column value to a row value, you will find the proportion of data falling to the left the z score with the given ones, tenths, and hundredths place values.
    ::z 的分数沿表外线垂直和水平运行。Z 分数的可能位置和十分位值沿表左侧垂直运行。Z 分数的可能位置和十分位值沿表顶部水平运行。当您将一列值与一行值匹配时,您会发现数据在左端的 z 分数与给定的位值、 十分、 100 位值的比例。

    Discussion Question: What is the approximate area under the normal distribution curve to the left of a z score of –6.05? What about to the left of  4.51?
    ::讨论问题:正常分布曲线下至z分-6.05分左侧的大致面积是多少? 4.51分左侧的大致面积是多少?

    Activity 2: Using the Standard Normal Distribution Table
    ::活动2:使用标准正常分配表

    Now that we understand the standard normal distribution table, we can use it to solve problems. The standard normal distribution below represents the heights of Redwood trees heights, discussed in the introduction.
    ::既然我们理解标准正常分布表, 我们可以用它解决问题。 下面的标准正常分布是红木树高的高度, 在导言中讨论过。

    Example
    ::示例示例示例示例

    The standard normal distribution is used to represent the distribution of Redwood trees heights. Use a standard normal distribution table to approximate the percentage of Redwood trees that have heights of greater than 2.37 standard deviations above the mean.
    ::标准正常分布用于表示红木树高的分布。使用标准正常分布表来估计红木树高高于平均值2.37标准偏差的百分比。

    Using the table, we can see that the proportion of area that falls to the left of 2.37 standard deviations above the mean is 0.9911. Values to the left of a z score represent Redwood trees that have a smaller height than a tree with a z score of 2.37. The problem here is that we need to know the proportion of Redwood trees that have a height greater than 2.37 standard deviations above the mean.
    ::使用该表,我们可以看到,落在高于平均值2.37标准偏差左边的面积比例是0.9911。 z分左边的值表示红木树的高度小于正正值2.37的树。这里的问题是,我们需要知道红木树的高度高于平均值2.37标准偏差的比例。

    lesson content
    Normally distributed data with a z score at 2.37. The area above the z score is displayed.

    Since we know that the area underneath the standard normal distribution is 1, we can subtract the proportion given by the table from 1 to find the area to the right of a z score.
    ::由于我们知道标准正常分布下的面积为1,我们可以将表给出的比例从1减去1,以找到该面积,再减为z分右。

    1 – 0.9911 = 0.0089

    Answer: 0.89% of Redwood trees have a height greater than 2.37 standard deviations above the mean.
    ::答复:0.89%的红木树的高度高于平均值2.37标准差。

    Since the standard normal distribution is symmetric, another way to find the value above a z score is to look up the opposite z score. When we look up –2.37 on the table, we see a proportion of 0.0089.
    ::由于标准正态分布是对称的,找到z分以上值的另一个方法是向相反的z分看。 当我们向上看-2.37时,我们看到的比例是0.0089。

    Example
    ::示例示例示例示例

    Use a standard normal distribution table to approximate the percentage of Redwood trees that have heights between the z scores of 0.5 and 1.5.
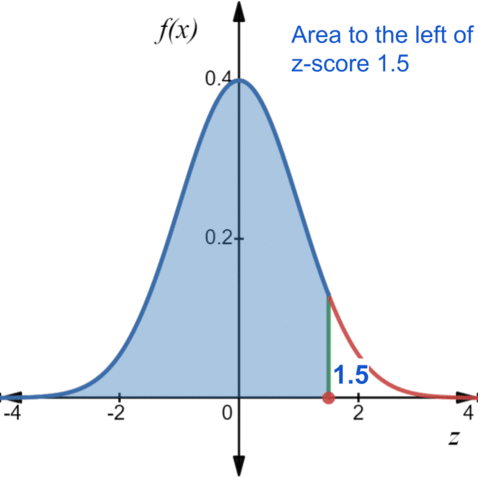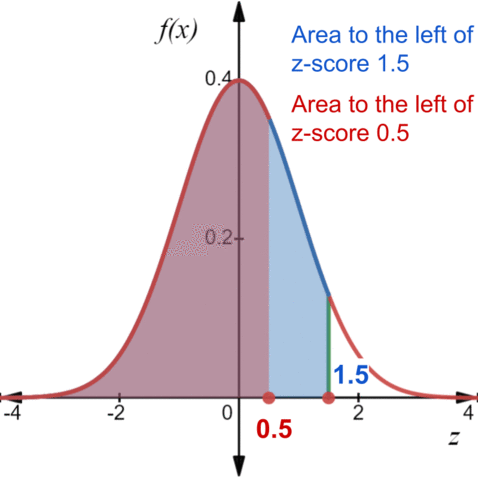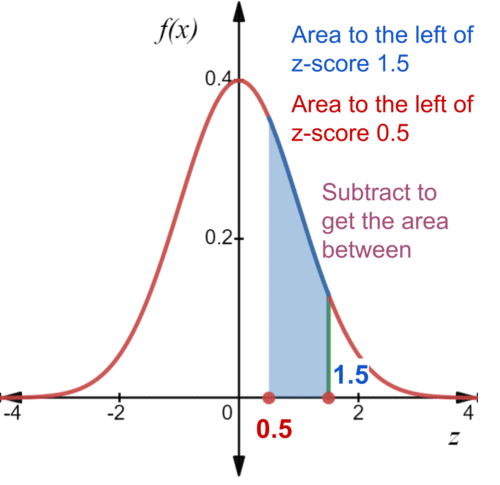
    ::使用标准正常分布表,以估计红木树在Z分数0.5至1.5之间高度的百分比。

    To find the proportion of area between two z scores, we need to take the z score farther to the right and cut off the excess area on the left. The area between two z scores can be found by subtracting the proportion to the left of the lesser z score from the proportion of area to the left of the greater z score.
    ::为了找到两个z分之间的区域比例,我们需要将z分向右,并切断左侧的多余区域。两个z分之间的区域可以通过从区域比例中减去较小z分对左的比例来找到。

    • The proportion of area to the left of a z score of 1.5 is 0.9332.
      ::面积在1.5兹分的左边的比例为0.9332。
    • The proportion of area to the left of a z score of 0.5 is 0.6915.
      ::面积在0.5兹分的左边的比例为0.6915。
    lesson content
    Subtract the area to the left of one z score from the area to the left of another to find the area between.

    0.9332 − 0.6915 = 0.2417

    Answer: 24.17% of Redwood trees should have a height between 0.5 standard deviations above the mean and 1.5 standard deviations above the mean.
    ::答复:24.17%的红木树的高度应高于平均值0.5个标准偏差,高于平均值1.5个标准偏差。

    Use the interactive below to practice finding proportions of the area in the standard normal distribution.
    ::使用以下互动方式在标准正常分布中找到区域比例。

    Activity 3: Intervals in the Standard Normal Distribution
    ::活动3:标准正常分配制的间隔

    The final step of mastering the standard normal distribution is to match a z score to a given percentage. We can do this by reversing the standard normal distribution table.
    ::掌握标准正态分布的最后一步是将z分与给定百分比匹配。 我们可以通过颠倒标准正态分布表来做到这一点 。

    Example
    ::示例示例示例示例

    Jeff wants to know what heights of Redwood trees should fall in the top five percent of heights. Use a standard normal distribution table to determine which z score will mark the expected top 5% of population data values.
    ::Jeff想知道红木树的高度应该跌到最高5%的高度。 使用标准正常分布表来确定哪个z分将标志着预期的人口数据值最高5%。

    Knowing that the combined area of the standard normal distribution is 1, the z score that marks the top 5% will also mark the bottom 95%. Thus if we look within the table for the closest proportion to 0.9500, the corresponding z score will be the one that we are looking for.
    ::由于知道标准正态分布的合并区域是 1, 标记最高5%的z分也代表底部95%。 因此,如果我们在表格中查看最接近0. 9500的比例,对应的z分将是我们正在寻找的。

    • The proportion of 0.9500 is closest to the z score of 1.64.
      ::0.9500的比例最接近1.64的z分。

    Answer: The z score 1.64 will mark the top 5% of data values. Any z score greater than or equal to 1.64 will fall in the top 5% of data values.
    ::回答:z分1.64将代表数据值的前5%。超过或等于1.64的z分将降为数据值的前5%。

    We could have also used the opposite z score to find this value as well. Since the distribution is symmetric and the table only tells us the proportion of data below the z score, we can begin by looking for the z score that is closest to the proportion 0.05.
    ::我们也可以用相反的z分来找到这个值。 由于分布是对称的,而表格只告诉我们z分以下的数据比例,我们可以首先寻找最接近0.05比例的z分。

    • The proportion 0.0500 is closest to the z score –1.64.
      ::比例为0.0500,最接近z分-1.64。

    The z score –1.64 marks the bottom 5% of data values, and conversely, the z score 1.64 will mark the top 5% of data values.
    ::z点 -1.64是数据值的底部5%,反之,z点1.64将是数据值的顶部5%。

    Discussion Question: Can you find the z scores that between which 35% of the data values will fall? What problems arise when attempting to figure this out?
    ::讨论问题:你能找到35%的数据值下降的z分数吗?在试图找出答案时会出现什么问题?

      Summary
    • The normal distribution function is
      N ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2

      ::正常的分布函数为 N( x) = 1-19632e- (x) 222- 132 。
    • Z score tables can be used to find the proportion of data falling to the left of a given z score.
      ::Z得分表可用于发现数据跌落到给定z得分左侧的比例。

    Wrap-Up: Review Questions
    ::总结:审查问题