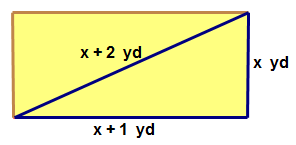节: 通过写作和解决单一可变等量来解决现实世界问题 | 1.12 通过写作和解决单一可变等量,解决现实世界问题

章节大纲

lesson content

Sheldon is watching his sister, Tracie, build triangles with red popsicle sticks. Tracie challenges him to tell her how many triangles she can build with 21 popsicle sticks. How can Sheldon use a table and an equation to figure this out?
::Sheldon正在看着他妹妹Tracie 用红冰棒棒建立三角形 Tracie要他告诉她她可以用21根冰棒棒建立多少三角形

In this concept, you will learn to solve real-world problems by writing and solving single- variable equations.
::在这个概念中,你将学会通过写作和解决单一可变方程式来解决现实世界的问题。

Solving Single Variable Equations
::解决单一变量

Writing an equation to model a real-world problem is often easier when you take the information given in the problem and express it in verbal form by using a few key words. This is very similar to translating verbal phrases into variable expressions. The difference is you will be translating a verbal sentence into an equation. Then, you can solve the equation using inverse operations .
::写一个方程式来模拟真实世界问题通常比较容易, 当您使用几个关键词来将问题中提供的信息以口头形式表达出来时。这与将口头短语转换为变量表达式非常相似。区别在于您会将一个口头句转换成一个方程式。然后, 您可以使用反向操作来解析方程式。

Let’s look at an example.
::让我们举个例子。

Monica purchased a pair of tennis shoes that had this sticker on the bottom of the shoe.
::莫妮卡买了一双网球鞋鞋底贴了贴纸

\begin{aligned} \begin{array}{rcl} $ 99.00 \\ $ 65.99 \end{array} \end{aligned}

Use a verbal model to write and solve an equation to determine the amount of money Monica saved by purchasing the shoes on sale.
::使用口头模型来写和解答一个方程式来决定Monica通过买鞋而节省的金额

First, write a verbal model to represent the problem.
::首先,写一个口头模型来代表问题。

Verbal Model: $\begin{aligned} Sales Price + Amount Saved = Original Price \end{aligned}$
::口头意见模式:销售价格+节省的金额=原件价格

Next, name the variable.
::下一位, 命名变量。

Let ‘ $\begin{aligned} s \end{aligned}$ ’ represent the amount saved.
::让我们 's ' 表示保存的金额。

Next, express the verbal model as an equation.
::接下来,用语言模型表达为方程式。

\begin{aligned} \begin{array}{rcl} \underset{65.99}{\underset{⏟}{Sale Price}} + \underset{s}{\underset{⏟}{Amount Saved}} & = & \underset{99.00}{\underset{⏟}{Original Price}} \\ 65.99 + s & = & 99.00 \end{array} \end{aligned}

::销售价格=65.99+Amount Saveds=原件价格=999.0065.99+s=99.00

Next, solve the equation you have written. Remember an equation is like a balance scale. To keep the scale balanced, what you do to one side of the equation you must also do to the other side. When solving an equation your goal is to isolate the variable on one side of the equation and the numerical terms on the other side. This is done by performing inverse operations.
::下一步, 解答您所写的方程式。记住一个方程式就像一个平衡比例尺。为了保持比例尺平衡, 您必须对方程式的一边做什么, 您也必须对另一方做什么。在解析方程式时, 您的目标是将方程式一边的变量和另一边的数字条件分离出来。这是通过执行反向操作完成的。

\begin{aligned} 65.99 + s = 99.00 \end{aligned}

::65.99+s=99.00

First, isolate the variable ‘ $\begin{aligned} s \end{aligned}$ ’ by subtracting 65.99 from both sides of the equation. Subtraction is the inverse of addition .
::首先,从方程的两侧减去65.99,将变量 ' s ' 分离出来。减法是反之。

\begin{aligned} 65.99 - 65.99 + s = 99.00 - 65.99 \end{aligned}

::65.99-65.99+s=99.00-65.99

Next, simplify each side.
::接下来,把每一边都简化一下

\begin{aligned} s = 33.01 \end{aligned}

::=33.01 s=33.01

The answer is $33.01.
::答案是33.01美元

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Sheldon’s red popsicle stick challenge.
::Sheldon的红冰棒球棒挑战引发了问题。

Sheldon needs to tell his sister how many triangles she can make with 21 popsicle sticks.
::Sheldon需要告诉他妹妹她能用21根冰棒棒做多少三角形

To figure out the number of triangles, Sheldon has to write an equation to represent the pattern .
::Sheldon要找出三角形的数目就必须写一个方程来代表图案

First, create a table of values.
::首先,创建一个数值表。

Number of Triangles "> $\begin{aligned} (n) \end{aligned}$	1	2	3	4	...	$\begin{aligned} n \end{aligned}$
Number of popsicle sticks $\begin{aligned} (p) \end{aligned}$	3	5	7	9			21

Next, write down the information in the table.
::接下来,写下表格中的信息。

For the first triangle $\begin{aligned} n = 1 \end{aligned}$ and $\begin{aligned} p = 3 \end{aligned}$ .
::第一个三角形 n=1 和 p=3 。

For the second triangle $\begin{aligned} n = 2 \end{aligned}$ and $\begin{aligned} p = 5 \end{aligned}$ .
::第二个三角形 n=2 和 p=5 。

For the third triangle $\begin{aligned} n = 3 \end{aligned}$ and $\begin{aligned} p = 7 \end{aligned}$ .
::第三个三角形 n=3 和 p=7 。

For the fourth triangle $\begin{aligned} n = 4 \end{aligned}$ and $\begin{aligned} p = 9 \end{aligned}$ .
::第四三角形 n=4 和 p=9 。

Next, model the information by writing a verbal model.
::其次,以写出一个口头模型作为资料的模型。

Verbal Model: Twice the number of triangles plus 1 equals 21.
::口头模式:三角形数的两倍加1等于21。

Next, write and solve a single- variable equation to model the problem.
::下一步,写并解决一个单一变量方程式来模拟问题。

\begin{aligned} 2 n + 1 = 21 \end{aligned}

::2n+1=21

Next, isolate the variable by subtracting one from both sides of the equation.
::下一步,从方程两侧减去一个变量,从而分离变量。

\begin{aligned} 2 n + 1 - 1 = 21 - 1 \end{aligned}

::2n+1-1=1=21-1

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

\begin{aligned} 2 n = 20 \end{aligned}

::2n=20

Then, divide both sides of the equation by 2 to solve for ‘ $\begin{aligned} n \end{aligned}$ ’.
::然后将方程式两边除以2,

\begin{aligned} \begin{array}{rcl} \frac{^{1} 2 n}{2} & = & \frac{20}{2} \\ n & = & 10 \end{array} \end{aligned}

::12n2=2020n=10

The answer is 10.
::答案是10个

Sheldon can tell his sister she can build 10 triangles with 21 popsicle sticks.
::Sheldon可以告诉他妹妹她可以建10个三角形加上21根冰棒棒

Example 2
::例2

Determine the number of cattle using a single-variable equation.
::使用单变量方程式确定牛的数量。

Six times the number of cattle less 87 is 999.
::牛数量是牛数量(87)的六倍,是牛数量(999)的六倍。

First, name the variable.
::首先, 命名变量。

Let ‘ $\begin{aligned} c \end{aligned}$ ’ represent the number of cattle.
::让 'c ' 代表牛的数量。

Next, express the statement as an equation.
::接下来,以方程式表示声明。

\begin{aligned} \begin{array}{rcl} \underset{6 c}{\underset{⏟}{Six times the number of cattle}} \underset{- 87}{\underset{⏟}{less 87}} \underset{= 999}{\underset{⏟}{is 999}} \\ 6 c - 87 = 999 \end{array} \end{aligned}

::牛数量是牛数量的六倍*6cless 878787is 9999996c-87=999

Next, isolate the variable by adding 87 to both sides of the equation. Addition is the inverse of subtraction.
::接下来,通过在方程的两侧增加87个变量来孤立变量。添加是逆减法。

\begin{aligned} 6 c - 87 + 87 = 999 + 87 \end{aligned}

::6c-87+87=999+87

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

\begin{aligned} 6 c = 1086 \end{aligned}

::6c=1086

Then, divide both sides of the equation by 6 to determine the value of ‘ $\begin{aligned} c \end{aligned}$ ’. Division is the inverse of multiplication .
::然后,将方程两侧除以 6 , 以确定 ' c ' 的价值。分法是乘法的逆数。

\begin{aligned} \begin{array}{rcl} \frac{^{1} 6 c}{6} & = & \frac{1086}{6} \\ c & = & 181 \end{array} \end{aligned}

::16c6=10866c=181

The answer is 181.
::答案是181个。

Example 3
::例3

A safety fence around a swimming pool has a rectangular gate entrance to the pool area.
::游泳池周围的安全栅栏有一个长方形门入口进入游泳池区域。

If the perimeter of the triangle outlined in dark blue is 12 yards, write and solve an equation to determine the lengths of the sides of the triangle.
::如果以暗蓝色绘制的三角形周边是12码,请写和解析一个方程,以确定三角形两侧的长度。

First, name the variable.
::首先, 命名变量。

Let ‘ $\begin{aligned} x \end{aligned}$ ’ represent the unknown length.
::让 'x ' 代表未知的长度。

Next, write an equation to represent the perimeter of the triangle. Remember the perimeter is the sum of the lengths of the three sides of the outlined blue triangle.
::接下来,写一个方程以表示三角形的周边。记住, 周边是蓝色三角形三侧的长度总和。

\begin{aligned} \begin{array}{rcl} x + (x + 1) + (x + 2) & = & 12 \\ x + x + 1 + x + 2 & = & 12 \end{array} \end{aligned}

::x+(x+1)+(x+2)=12x+x+1+x+2=12

Next, simplify the left side of the equation by collecting like terms .
::接下来,通过收集类似条件来简化方程式的左侧。

\begin{aligned} 3 x + 3 = 12 \end{aligned}

::3x+3=12 3x+3=12

Next, isolate the variable by subtracting three from both sides of the equation.
::接下来,从方程的两侧减去三,将变量分离出来。

\begin{aligned} 3 x + 3 - 3 = 12 - 3 \end{aligned}

::3x+3-3-3=12-3

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

\begin{aligned} 3 x = 9 \end{aligned}

::3x=9

Next, divide both sides of the equation by 3 to solve for ‘ $\begin{aligned} x \end{aligned}$ ’.
::接下来,将方程式两边除以3,

\begin{aligned} \begin{array}{rcl} \frac{^{1} 3 x}{3} & = & \frac{9}{3} \\ x & = & 3 \end{array} \end{aligned}

::13x3=93x=3

The answer is 3.
::答案是3

Then, substitute $\begin{aligned} x = 3 \end{aligned}$ into the length for each of the three sides of the triangle.
::然后,将三角形三边的长度分别替换为 x=3 。

\begin{aligned} \begin{array}{rcl} x + (x + 1) + (x + 2) & = & 12 \\ 3 + (3 + 1) + (3 + 2) & = & 12 \\ x & = & 3 y d \\ x + 1 & = & 4 y d \\ x + 2 & = & 5 y d \end{array} \end{aligned}

::x+(x+1)+(x+2)=123+(3+1)+(3+2)=12x=3 ydx+1=4 ydx+2=5 yd

Example 4
::例4

Jonas is working with his Uncle Tim as an apprentice electrician wiring a new house. For each job that Jonas works, he is paid a one-time service fee of $50.00 plus $25.00 an hour. When the house was completely wired, Uncle Tim paid Jonas $2250.00.
::Jonas和他叔叔Tim一起工作,作为学徒电工,为Jonas打通新房子,每次工作都向他支付一次性服务费50美元加25美元,每小时25美元。当房子完全电线接通时,Tim叔叔付给Jonas220.00美元。

Write and solve an equation to determine the number of hours Jonas worked wiring the house.
::写和解决一个方程式以确定Jonas在房子的电线上工作的时间

First, name the variable.
::首先, 命名变量。

Let ‘ $\begin{aligned} h \end{aligned}$ ’ be the number of hours Jonas worked.
::Jonas的工作时数。

Next, write a verbal model to represent the problem.
::接下来,写一个口头模型来代表问题。

Verbal Model: 25 times the number of hours worked plus the service fee is 2250.
::口头模式:25倍的工作小时数加服务费为2250。

Next, write a single-variable equation to represent the verbal model.
::接下来,写一个单变量方程式来代表语言模型。

\begin{aligned} \underset{25 h}{\underset{⏟}{25 times the number of hours worked}} \underset{+ 50}{\underset{⏟}{plus the service fee}} \underset{= 2250}{\underset{⏟}{is 2250}} \end{aligned}

::25小时 25小时服务费50 2250 2250

The single-variable equation is
::单变量方程式是

\begin{aligned} 25 h + 50 = 2250 \end{aligned}

::25小时+50=2250

Next, isolate the variable by subtracting 50 from both sides of the equation.
::接下来,从方程的两侧减去50,将变量分离出来。

\begin{aligned} 25 h + 50 - 50 = 2250 - 50 \end{aligned}

::25h+50-50=50-50=2250-50

Next, simplify both sides of the equation.
::接下来,简化方程式的两边

\begin{aligned} 25 h = 2200 \end{aligned}

::25小时=2200

Then, divide both sides of the equation by 25 to solve for ‘ $\begin{aligned} h \end{aligned}$ ’.
::然后将方程式两边除以25,

\begin{aligned} \begin{array}{rcl} \frac{^{1} 25 h}{25} & = & \frac{2200}{25} \\ h & = & 88 \end{array} \end{aligned}

::125h25=220025h=88

The answer is 88.
::答案是88岁

Review
::回顾

Write an equation for each situation and then solve for the variable. Each problem will have two answers.
::每个问题将有两个答案。

An unknown number and three is equal to twelve.
::一个未知的数字和三个等于12。

John had a pile of golf balls. He lost nine on the course. If he returned home with fourteen golf balls, how many did he start with?
::约翰有一堆高尔夫球他输了9个球如果他带着14个高尔夫球回家

Some number and six is equal to thirty.
::部分数和6等于30。

Jessie owes her brother some money. She earned nine dollars and paid off some of her debt. If she still owes him five dollars, how much did she owe him to begin with?
::Jessie欠她弟弟一些钱,她赚了9美元还清了部分债务,如果她还欠他5美元,她欠他多少钱?

A farmer has chickens. Six of them went missing during a snow storm. If there are twelve chickens left, how many did he begin with before the storm?
::农民养鸡,其中6只在暴风雪中失踪。如果还剩下12只鸡,那么在暴风雨之前,他从几只鸡开始?

Gasoline costs four dollars per gallon. Kerry put many gallons in his car over a long car trip. If he spent a total of $140.00 on gasoline, how many gallons did he need for the trip?
::汽油每加仑4美元。 Kerry在长途旅行中将许多加仑放在他的车里。如果他在汽油上花费了总共140美元,他需要多少加仑的汽油?

Twenty-seven times a number is 162. What is the number?
::数字27乘以162 号码是多少?

Marsha divided her cookies into groups of 12. IF she is able to make 6 groups, how many cookies did she start with?
::玛莎把她的饼干分成12组, 如果她能做6组,

The coach divided the students into five teams. There were fourteen students on each team. How many students did the coach begin with?
::教练把学生分成五组,每组有14名学生,教练开始时有多少学生?

A number plus nineteen is equal to forty.
::数加十九等于四十

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Solving Single Variable Equations ::解决单一变量

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Solving Single Variable Equations
::解决单一变量

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源