Section: 了解四边协定的速准措施 | 6.8 了解四边协定的速准措施

Section outline

Stephanie, a Math 12 student, is helping to raise money to participate in this year’s Math Olympiad in Dallas, Texas. Since Stephanie is very artistic in making jewelry, she has decided to make and sell necklaces to raise money. Several customers have asked her what shape she has used for the blue bead of a particularly geometric looking necklace. She knows what shape it is but is not sure of how to explain this shape to her customers.
::斯蒂芬妮(Matth 12 ) , 一位数学十二年级学生,正在帮助筹集资金参加今年在得克萨斯州达拉斯举行的数学奥林匹亚会。由于斯蒂芬妮在制作首饰方面非常有艺术性,她决定制作和出售项链以筹集资金。几位顾客问她用什么形状来制作一个特别几何项链子的蓝珠子。她知道是什么形状,但不知道如何向客户解释这一形状。

What can Stephanie tell her customers about this shape?
::Stephanie能告诉客户什么?

In this concept, you will learn to understand the angle measures of quadrilaterals.
::在这个概念中,你会学会理解四边形的角度量。

Quadrilaterals
::四方

A quadrilateral is a two-dimensional closed shape that has four straight sides.
::四边形是两维封闭的形状,有四个直面。

Three special quadrilaterals are a which is a quadrilateral with opposite sides parallel and congruent , a trapezoid which is a quadrilateral that has one pair of opposite sides parallel and a which is a quadrilateral that has two pairs of congruent adjacent sides.
::三个特殊的四边形是四边形,两边平行,一对相近,四边形,四边形,一对对对立,四边形,四边形,两对相邻,四边形。

Three special parallelograms are a rectangle which has every angle a right angle and opposite sides both congruent and parallel, a square which has every angle a right angle, opposite sides parallel and all sides congruent and a rhombus which has every side equal in length, opposite sides parallel, but not every angle is a right angle.
::三个特殊的平行图是一个矩形,每个角都有一个右角,对面的对角都具有相近和平行的对角,一个每个角都有一个右角,对面平行,所有两边都具有对齐,一个每边长度相等,对面平行,但并不是每个角都是对角的对角。

Remember a quadrilateral is a two-dimensional closed shape that has four straight sides and four angles.
::记住一个四边形是一个二维封闭的形状, 它有四个直面和四个角度。

The sum of the interior angles of a quadrilateral is 360° regardless of the type of quadrilateral. The following diagram will show various quadrilaterals and their interior angles.
::四边形的内部角总和为360°,而不论四边形的类型。下图将显示各种四边形及其内部角。

If you add the measure of the four interior angles of each quadrilateral shown above, the sum will equal 360°. Each of these quadrilaterals can be divided into two triangles. Remember the sum of the interior angles of a triangle equals 180°. If the closed figure contains two triangles then the sum of the interior angles equals $\begin{aligned} 2 (180^{\circ}) = 360^{\circ} \end{aligned}$ .
::如果您添加上面显示的每个四边形的四个内部角度的度量, 数值将等于360°。这些四边形中的每一个都可以分为两个三角形。记住一个三角形的内部角度和等于180°。如果封闭的图中包含两个三角形, 那么内角的和等于2( 180)=360。

Let’s apply these facts to an example.
::让我们把这些事实应用到一个例子上。

For the following quadrilateral, determine the measure of $\begin{aligned} ∠ M \end{aligned}$ .
::对于以下四边形,确定 M 的量度。

First, write an equation to represent the sum of the interior angles of quadrilateral $\begin{aligned} J K L M \end{aligned}$ .
::首先,写一个方程,以表示四边形JKLM的内部角度之和。

$\begin{aligned} ∠ J + ∠ K + ∠ L + ∠ M = 360^{\circ} \end{aligned}$

::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

Next, substitute into the equation, the given measures of angles $\begin{aligned} J, K \end{aligned}$ and $\begin{aligned} L \end{aligned}$ .
::其次,用方程式来替代角度的量度 J、K和L

$\begin{aligned} \begin{array}{rcl} ∠ J + ∠ K + ∠ L + ∠ M & = & 360^{\circ} \\ 77^{\circ} + 90^{\circ} + 128^{\circ} + ∠ M & = & 360^{\circ} \end{array} \end{aligned}$

::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} 77^{\circ} + 90^{\circ} + 128^{\circ} + ∠ M & = & 360^{\circ} \\ 295^{\circ} + ∠ M & = & 360^{\circ} \end{array} \end{aligned}$

::7790128M=360295M=360

Then, subtract $\begin{aligned} 295^{\circ} \end{aligned}$ from both sides of the equation to solve for the measure of $\begin{aligned} ∠ M \end{aligned}$ .
::然后从方程的两侧减去295 以解答 QM 的度量。

$\begin{aligned} \begin{array}{rcl} 295^{\circ} + ∠ M & = & 360^{\circ} \\ 295^{\circ} - 295^{\circ} + ∠ M & = & 360^{\circ} - 295^{\circ} \\ ∠ M & = & 65^{\circ} \end{array} \end{aligned}$

The answer is 65.

The measure of $\begin{aligned} ∠ M \end{aligned}$ is 65°.
::度量为65度。

This method can be used to calculate the measure of the missing angle of any quadrilateral when the measures of three of the angles are known.
::当已知三个角度的度量时,可以使用这种方法计算任何四边形缺失角的度量。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Stephanie and her necklaces. She needs to figure out what to tell her customers about the shape of the blue bead. What can she tell them?
::早些时候,你对Stephanie和她的项链有疑问她需要知道怎么告诉她的客户蓝珠的形状

First, draw the shape and include all important markings.
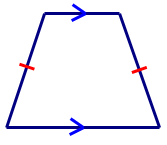
::首先,绘制形状,包括所有重要的标记。

Next, explain the markings on the sides of the shape.
::接下来,请解释形状两侧的标记。

The arrows on the top and bottom sides of the figure indicate that this pair of opposite sides are parallel. The tic mark on the other two sides indicate that these sides are congruent (equal in length).
::数字上方和下方的箭头显示,这对对对立面是平行的。另外两边的口号显示,两边是相同的(长度相等 ) 。

Then, name the shape.
::然后,命名形状。

The shape of the blue bead is an isosceles trapezoid .
::蓝色珠子的形状是一个等骨类类。

Example 2
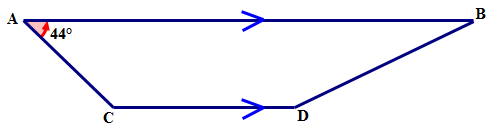
::例2

A quadrilateral $\begin{aligned} A B C D \end{aligned}$ having one pair of opposite sides parallel has angle measures such that $\begin{aligned} ∠ A = 44^{\circ} \end{aligned}$ . Find the measure of $\begin{aligned} ∠ C \end{aligned}$ in the following quadrilateral.
::A=44。在以下四边方中查找 C 的度量。

First, name the type of quadrilateral and write down what you know.
::首先,命名四边形的类型, 并写下你知道的。

A quadrilateral with one pair of opposite sides parallel is called a trapezoid. $\begin{aligned} ∠ A \end{aligned}$ and $\begin{aligned} ∠ C \end{aligned}$ are on the same side of leg $\begin{aligned} ∠ A C \end{aligned}$ and are supplementary.
::双向平行的四边形称为“陷阱状” 。 A 和 C 位于 AC 腿的同一侧, 具有补充性。

Next, write an equation to model what you know about the two angles.
::接下来,写一个方程来模拟你对这两个角度的了解。

$\begin{aligned} ∠ A + ∠ C = 180^{\circ} \end{aligned}$

::AC=180

Next, fill into the equation the measure of $\begin{aligned} ∠ A \end{aligned}$ .
::接下来,填入QA的度量方程式。

$\begin{aligned} \begin{array}{rcl} ∠ A + ∠ C = 180^{\circ} \\ 44^{\circ} + ∠ C = 180^{\circ} \end{array} \end{aligned}$

::C=180 44 C=180 C=180

Then, subtract 44° from both sides of the equation to solve for $\begin{aligned} ∠ C \end{aligned}$ .
::然后从方程的两侧减去44度,以解答 QC 。

$\begin{aligned} \begin{array}{rcl} 44^{\circ} + ∠ C & = & 180^{\circ} \\ 44^{\circ} - 44^{\circ} + ∠ C & = & 180^{\circ} - 44^{\circ} \\ ∠ C & = & 136^{\circ} \end{array} \end{aligned}$
The answer is 136.

The measure of $\begin{aligned} ∠ C \end{aligned}$ is 136°.
::°C的度量为136°。

Example 3
::例3

For the following quadrilateral, find the measure of the unknown angle.
::对于以下四边形,找到未知角的度量。

First, write an equation to model the sum of the interior angles of a quadrilateral.
::首先,写一个方程来模拟四边形内角的总和。

$\begin{aligned} ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 360^{\circ} \end{aligned}$

Next, fill into the equation the measures of any known angles.
::接下来,填入方程式中任何已知角度的度量。

$\begin{aligned} \begin{array}{rcl} ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 & = & 360^{\circ} \\ 105^{\circ} + 75^{\circ} + 60^{\circ} + ∠ 4 & = & 360^{\circ} \end{array} \end{aligned}$

Next, let $\begin{aligned} ∠ 4 = x \end{aligned}$
::下一步,让 @ 4=x

$\begin{aligned} \begin{array}{rcl} 105^{\circ} + 75^{\circ} + 60^{\circ} + ∠ 4 & = & 360^{\circ} \\ 105^{\circ} + 75^{\circ} + 60^{\circ} + x & = & 360^{\circ} \end{array} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}105 75 75 *60 *x=360 * {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} 105^{\circ} + 75^{\circ} + 60^{\circ} + x & = & 360^{\circ} \\ 240^{\circ} + x & = & 360^{\circ} \end{array} \end{aligned}$

::1057560x=360240x=360

Next, subtract 240° from both sides of the equation to solve for ‘ $\begin{aligned} x \end{aligned}$ ’.
::下一步,从方程的两侧减去240°,以解析 `x ' 。

$\begin{aligned} \begin{array}{rcl} 240^{\circ} + x & = & 360^{\circ} \\ 240^{\circ} - 240^{\circ} + x & = & 360^{\circ} - 240^{\circ} \\ x & = & 120^{\circ} \end{array} \end{aligned}$

The answer is 120.
::答案是120个

The measure of $\begin{aligned} ∠ 4 \end{aligned}$ is 120°.
::4°C的度量为120°。

Example 4
::例4

What is the measure of the fourth angle of a quadrilateral which has three angles that measure 110°, 80° and 95°?
::一个四边形的第四个角度有3个角度,测量度为110°、80°和95°,该角度的量度是多少?

First, write an equation to model the sum of the interior angles of the quadrilateral.
::首先,写一个方程来模拟四边形内角的总和。

$\begin{aligned} ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 360^{\circ} \end{aligned}$

Next, fill into the equation the measures of the three known angles.
::接下来,填入方程式中三个已知角度的量度。

$\begin{aligned} \begin{array}{rcl} ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 & = & 360^{\circ} \\ 110^{\circ} + 95^{\circ} + 80^{\circ} + ∠ 4 & = & 360^{\circ} \end{array} \end{aligned}$

Next, simplify the left side of the equation.
::接下来,简化方程的左侧。

$\begin{aligned} \begin{array}{rcl} 110^{\circ} + 95^{\circ} + 80^{\circ} + ∠ 4 & = & 360^{\circ} \\ 285^{\circ} + ∠ 4 & = & 360^{\circ} \end{array} \end{aligned}$

Then, subtract 285° from both sides of the equation to solve for the measure of $\begin{aligned} ∠ 4 \end{aligned}$ .

$\begin{aligned} \begin{array}{rcl} 285^{\circ} + ∠ 4 & = & 360^{\circ} \\ 285^{\circ} - 285^{\circ} + ∠ 4 & = & 360^{\circ} - 285^{\circ} \\ ∠ 4 & = & 75^{\circ} \end{array} \end{aligned}$

Example 5
::例5

What is the name of the quadrilateral that has all sides equal in length, opposite sides parallel and every angle a right angle?
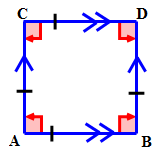
::四边形的四边形的名称是什么,四边形的长度相等,对立面平行,每个角度都有一个正确的角度?

First, draw the quadrilateral to represent the information given in the problem.
::首先,绘制四边形以代表问题中所提供的信息。

Then, name the quadrilateral.
::那就给四边形取个名字吧

This is a special parallelogram called a square .
::这是一个特殊的平行图,叫做方形。

Review
::回顾

Use what you have learned about quadrilaterals to figure out the missing angle measure of each quadrilateral based on three given angles.
::使用您所学到的关于四边形的知识来根据三个给定角度找出每个四边形缺失的角度量。

120°, 120°, 60°, ?

50°, 70°, 130°, ?

52°, 128°,52°, ?

47°, 55°, 120°, ?

80°, 80°, 100°, ?

105°, 105°, 85°, ?

97°, 97°, 35°, ?

120°, 120°, 40°, ?

88°, 90°, 60°, ?

25°, 85°, 85°, ?

90°, 90°, 90°, ?

140°, 150°, 45°, ?

80°, 80°, 120°, ?

75°, 95°, 110°, ?

80°, 50°, 95°, ?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Quadrilaterals ::四方

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Quadrilaterals
::四方

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)