报 认 反 反 反

播放段落

Kevin and his sister Kim went to visit their great aunt in the country. On the drive in, they enjoyed looking at the scenery. It was so different from their home in the city. As they turned down the drive leading up to the estate, Kim gasped at the lovely tree lined road.
::Kevin和他的妹妹Kim去拜访了他们在该国的姑姑。在开车时,他们喜欢看风景。这与他们在城里的家大不相同。当他们拒绝开往庄园的车时,Kim在可爱的树条路上被加了油。

播放段落

“Look at the symmetry! It’s a reflection!” Kim exclaimed. Kevin is not sure what this means, how can Kim explain it to him?
::“看看对称性!这是一个反射! ”Kim发言说。 Kevin不知道这意味着什么,Kim怎么能向他解释呢?

播放段落

In this concept, you will learn to recognize reflections.
::在这个概念中,你会学会认识思考。

播放段落

Reflections
::反思

播放段落

Congruent figures are created by using transformations . A transformation is a move in some way. One kind of transformation is called a reflection or a flip.
::Congruent 数字是用变换来生成的。 变换是某种方式的动作。 一种变换被称为反射或翻转。

播放段落

Look at the figures below. Each of the figures can be reflected over a line of reflection.
::看看下面的数字,每个数字都可以从一线反省反映出来。

播放段落

You can also find reflections on the coordinate plane .
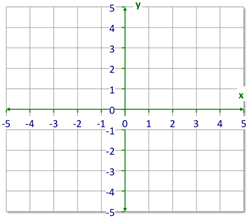
::您也可以在坐标平面上找到反射。

播放段落

To understand reflection transformations, a review of the coordinate plane is necessary. A reflection performed on the coordinate plane is provides a visual representation of the transformation. The coordinate plane is a representation of two-dimensional space . It has a horizontal axis, called the $\begin{align*}x\end{align*}$ -axis, and a vertical axis, called the $\begin{align*}y\end{align*}$ -axis.
::为了理解反射转换,有必要对坐标平面进行审查。在坐标平面上进行的反射可以直观地表示变形。坐标平面代表二维空间。它有一个横向轴,称为X轴,和一个垂直轴,称为Y轴。

播放段落

Geometric figures can be graphed and moved on the coordinate plane. Here is a picture of the coordinate plane.
::几何数字可以绘制图表并移动到坐标平面上。这是坐标平面的图片。

播放段落

Look at the image below.
::看看下面的图像。

播放段落

The image on the right is the pre-image or the triangle to which the transformation will be applied. This triangle has been reflected over the $\begin{align*}y\end{align*}$ -axis because the $\begin{align*}y\end{align*}$ -axis is acting like a mirror for the two triangles. This line that acts like the mirror when a reflection occurs is called the line of reflection . The triangle on the left is the image or the result of the triangle on the right being reflected over the $\begin{align*}y\end{align*}$ -axis.
::右侧的图像是图像预映像, 或要应用转换的三角形。 这个三角形已经反映在 Y 轴上, 因为 y 轴像两个三角形的镜像一样。 反射时的反射动作类似镜子的直线被称为反射线。 左边的三角形是图像或右侧三角形的结果, 反射到 y 轴上 。

播放段落

Imagine standing in front of a mirror and holding up your left hand. Where is your hand in the mirror’s reflection? A reflected figure works the same way: when you flip it over the line of reflection, all of its points are reversed.
::想象一下,站在镜子前,举起左手。 镜子反射中的你的手在哪里? 一个反射的图象也用同样的方式:当你把它翻过反射线时,它的所有点都倒转了。

播放段落

You can reflect an image over the $\begin{align*}x\end{align*}$ -axis or over the $\begin{align*}y\end{align*}$ -axis. These two lines of reflection will be used to perform reflections on the coordinate plane. The reflections performed on the coordinate plane can be described using coordinate notation .
::您可以在 X 轴或 Y 轴上反射图像。 这两条反射线将用于在坐标平面上进行反射。 在坐标平面上进行的反射可以通过协调符号描述。

播放段落

Let’s take a look at how to express a reflection using coordinate notation.
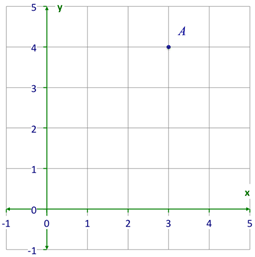
::让我们看看如何使用协调符号表达反思。

播放段落

The point A is plotted on the coordinate plane.
::A点是在坐标飞机上绘制的

播放段落

To write about point $\begin{align*}A\end{align*}$  being plotted, name it using an ordered pair to represent both its $\begin{align*}x\end{align*}$  and $\begin{align*}y\end{align*}$ -coordinates. An ordered pair is written in the form $\begin{align*}(x, y)\end{align*}$  where $\begin{align*}x\end{align*}$  is the $\begin{align*}x\end{align*}$ -coordinate and $\begin{align*}y\end{align*}$  is the $\begin{align*}y\end{align*}$ -coordinate of the plotted point.
::要写入正在绘制的 A 点, 请使用一对定购的对来表示它的 x 和 Y 坐标。 定购的对以 x 坐标为 x 坐标, y 坐标为 y 坐标的窗体( x, y) 写成。

播放段落

Therefore, Point $\begin{align*}A = (3, 4)\end{align*}$  has been represented using coordinate notation.
::因此,A点=(3 400)使用协调符号表示。

播放段落

When a figure is drawn on the coordinate plane, coordinate notation can be used to describe the figure drawn. If a triangle is drawn on a coordinate plane, then three sets of ordered pairs must be written to represent each vertex of the triangle.
::当在坐标平面上绘制数字时,可使用协调标记来描述所绘制的数字。如果在坐标平面上绘制三角形,则必须写出三组有顺序的配对,以代表三角形的每个顶点。

播放段落

Let’s look at an example.
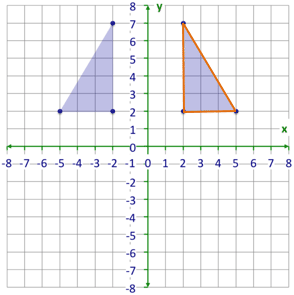
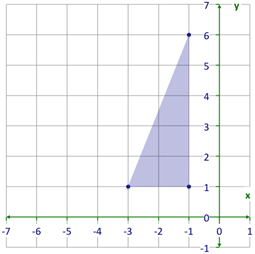
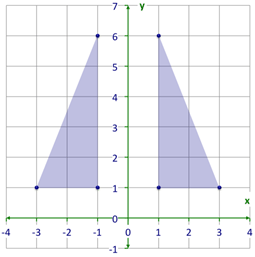
::让我们举个例子。

播放段落

This triangle has three vertices that can be named using coordinate notation as:
::此三角形有三个顶点, 可以使用坐标符号命名为 :

播放段落

(-1, 1), (-3, 1), and (-1, 6).
:-1,1,(3,1)和(1,6)

播放段落

If this triangle were reflected over the $\begin{align*}y\end{align*}$ -axis, what coordinate notation would be used to name its vertices?
::如果这个三角形在 Y 轴上反射, 将会使用什么坐标符号来命名它的顶部 ?

播放段落

The diagram below shows the preimage triangle on the left and the image triangle on the right.
::下图显示左边的预视三角形和右边的图像三角形。

播放段落

The image triangle (the one on the right side) has the following coordinates for vertices.
::图像三角形( 右侧的三角形) 具有以下顶点坐标 。

播放段落

(1, 1), (3, 1) and (1, 6)
:第1、1)、3、1和1、6)

播放段落

Let’s compare the coordinates of the two triangles side by side to see if there is a pattern.
::让我们比较两个三角形的坐标, 看看是否有模式。

播放段落

$$\begin{align*}\begin{array}{rcl} && \text{Triangle} - 1 \qquad \qquad \qquad \quad \quad \text{Triangle} - 2 \\ && \text{(left side - preimage)}\qquad \qquad \ \ \text{(right side - image)} \\ && (-1, 1) \qquad \qquad \qquad \qquad \qquad (1, 1) \\ && (-3, 1) \qquad \qquad \qquad \qquad \qquad (3, 1) \\ && (-1, 6) \qquad \qquad \qquad \qquad \qquad (1, 6) \\ \end{array}\end{align*}$$
::三角- 1 三角-2 左侧 - 预映射 (右侧 - 图像)(-1,1,1,1,1,1,1,3,1,3,1,1,6,6)

播放段落

You can see that the $\begin{align*}x\end{align*}$ -coordinates of the reflected triangle are opposite those of the first triangle.
::您可以看到,反射三角形的 X 坐标与第一个三角形的坐标相对。

播放段落

Remember, when figure is reflected over the $\begin{align*}y\end{align*}$  axis, the $\begin{align*}x\end{align*}$  coordinates are opposite in the reflection. When a figure is reflected over the $\begin{align*}x\end{align*}$  axis, the $\begin{align*}y\end{align*}$  coordinates are opposite in the reflection.
::记住,当图在 y 轴上方反射时, x 坐标在反射时是相反的。当图在 x 轴上方反射时,y 坐标在反射时是相反的。

播放段落

Now that you know the two rules for figuring out the coordinates of a figure reflected on the coordinate plane, so you can use those rules to figure out new reflections whether you have been given an image or not.
::现在你知道两个规则了 来找出坐标平面上反映的图的坐标, 这样你就可以用那些规则 来找出新的反省, 无论你是否获得了图像。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were given a problem about  Kim’s reflection.
::更早之前,

播放段落

Kim made the statement that she did because one side of the road is a perfect reflection of the other side. In other words, one side matches the other side. You could draw a line right down the center of the road separating the left side from the right side and the reflection would be perfect.
::金说她这样做是因为路的一面是另一面的完美反射。 换句话说, 一面与另一面相匹配。 你可以在路的中间画一条线,将左侧与右侧隔开,反射是完美的。

播放段落

Example 2
::例2

播放段落

What would be the new coordinates of a figure reflected over the $\begin{align*}x\end{align*}$ -axis?
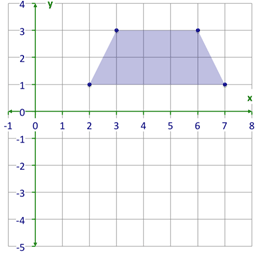
::X轴上反映的数字的新坐标是什么?

播放段落

First, look at this figure and write down the coordinates of this trapezoid .
::首先,看看这个图,写下这个形的坐标。

(2, 1)

(7, 1)

(3, 3)

(6, 3)

播放段落

Next, use the rule to figure out the new coordinates of the reflected trapezoid. This trapezoid is being reflected over the $\begin{align*}x\end{align*}$ -axis, so the $\begin{align*}y\end{align*}$ -coordinates will become the opposite while the $\begin{align*}x\end{align*}$ -coordinates remain the same.
::下一步, 使用此规则来找出反射 cuezoid 的新坐标 。 这个 cuezoid 正在被反射到 x 轴上, 所以 y 坐标会变成相反, 而 x 坐标则保持不变 。

播放段落

The new coordinates are:
::新的坐标是:

(2, -1)

(7, -1)

(3, -3)

(6, -3)

播放段落

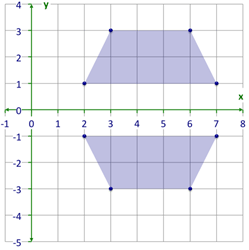
Then, graph the reflected trapezoid on the coordinate plane.
::然后绘制坐标平面上反射的形图

播放段落

This graph shows the reflection.
::此图显示反射 。

播放段落

The $\begin{align*}x\end{align*}$ -axis forms a line of reflection so that the trapezoid below the $\begin{align*}x\end{align*}$ -axis is the mirror image of the trapezoid above the $\begin{align*}x\end{align*}$ -axis.
::x 轴形成反射线,这样, x 轴下方的捕捉层是X 轴上方的捕捉层的镜像图像。

播放段落

Example 3
::例3

播放段落

Is this an example of a reflection?
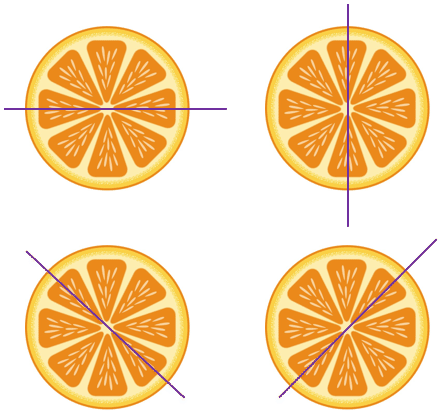
::这是反省的一个例子吗?

播放段落

First, determine if the figure can be divided into sides that are perfectly matched.
::首先,确定数字是否可以分为完全匹配的两面。

播放段落

Look at the orange slice. It looks like a line of symmetry can be drawn in four parts of the diagram to create mirror images.
::看看橙色的切片。 它看起来像一个对称线 可以绘制在图表的四部分 来创建镜像图像 。

播放段落

Next, draw the to see if this figure is an example of a reflection.
::接下来,请绘制下图,看看这个数字是否是一个反省的例子。

播放段落

The answer is yes.
::答案是肯定的。

播放段落

The figure can be divided so that one side perfectly matches the other.
::数字可以分开,以便一方与另一方完全吻合。

播放段落

Example 4
::例4

播放段落

Is this an example of a reflection?
::这是反省的一个例子吗?

播放段落

First, determine if the shape can be divided into sides that are perfectly matched.
::首先,确定形状是否可以分成 完全匹配的两边。

播放段落

It does not look like a line of symmetry can be drawn for this diagram to create mirror images.
::它看起来不像可以绘制此图表来创建镜像图像的对称线 。

播放段落

The answer is no.
::答案是否定的。

播放段落

Review
::回顾

播放段落

Define the following terms.
::界定以下术语。

播放段落

1. Reflection
::1. 反思

播放段落

2. Coordinate Plane
::2. 协调计划

播放段落

3. $\begin{align*}X\end{align*}$ -axis
::3. X轴

播放段落

4. $\begin{align*}Y\end{align*}$ -axis
::4. Y轴

播放段落

Write each set of coordinates for a reflection of each figure over the $\begin{align*}x\end{align*}$ -axis.
::写下每组坐标,以反映出 X 轴上的每一图。

5. (1, 3) (2, 5) (3, 2)

6. (2, 1) (5, 1) (2, 4)

7. (-1, 1) (-1, 3) (-4, 1)

8. (1, 2) (1, 5) (5, 2) (5, 5)

9. (1, 2) (6, 1) (6, 3) (2, 3)

10. (-1, 3) (-3, 1) (-5, 1) (-4, 6)

播放段落

Write a new series of coordinates for a figure reflected over the $\begin{align*}y\end{align*}$ -axis.
::为 Y 轴上反映的数字写出新的坐标序列 。

11. (1, 3) (2, 5) (3, 2)

12. (-1, 1) (-1, 3) (-4, 1)

13. (2, 1) (5, 1) (2, 4)

14. (1, 2) (1, 5) (5, 2) (5, 5)

15. (-1, 3) (-3, 1) (-5, 1) (-4, 6)

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。