节: 识别关系 | 6.18 承认关系

章节大纲

In the 1800s, the average house was $\begin{aligned} 20 \times 40 feet \end{aligned}$ . So the average area was 800 square feet. In order to create a model of a log cabin this size, you are going to use a scale factor of $\begin{aligned} \frac{1}{16} \end{aligned}$ . What will be the dimensions of the model?
::1800年代,平均房屋面积为20×40英尺。平均面积为800平方英尺。为了创建这样大小的木屋模型,您将使用116的尺度系数。模型的尺寸是什么?

In this concept, you will learn to recognize dilations.
::在这个概念中,你将学会识别膨胀。

Dilations
::关系

There are all kinds of transformations. You can flip or reflect a figure, translate or slide a figure and rotate a figure. You can also stretch or shrink a figure to create a new one. This is called a dilation . A dilation is a transformation created by a scale factor.
::各种变换都有。您可以翻转或反映一个图,翻译或幻灯片一个图,并旋转一个图。您也可以伸展或缩放一个图来创建一个新的图。这被称为“推算”。推算是指由比例因素造成的变换。

You can create a dilation that is smaller or larger than the original figure. Either way, a similar figure is created through a dilation.
::您可以创建一个小于或大于原始图象的比方。无论哪种方式,类似的图象都是通过一个比方创建的。

Let’s think about scale factors .
::让我们想想比额表因素。

The scale factor is the ratio that determines the proportional relationship between the sides of .
::比额表系数是确定......两侧之间比例关系的比率。

For the pairs of sides to be proportional to each other, they must have the same scale factor. In other words, similar figures have congruent angles and sides with the same scale factor. With a scale factor of two, each side of the larger figure is exactly twice as long as the corresponding side in the smaller figure.
::要使两边对齐,它们必须具有相同的比例系数。换句话说, 相近的数字具有相同的角度和边与比例系数。以两个比例系数计算, 较大数字的两边的两边是小数字对应方的两倍。

Let’s look at an example.
::让我们举个例子。

A figure has a side length of 3 feet. What would be the corresponding side length of the next figure if the scale factor were 4?
::一个数字的侧长为3英尺。如果比额表因数为4,下一个数字的相应侧长是多少?

You know the length of one of the sides of the first figure and you know the scale factor. To figure out the new length, you can multiply the scale factor times the first length.
::您知道第一个图的两边之一的长度, 您知道缩放系数。要找出新的长度, 您可以将缩放系数乘以第一个长度。

$\begin{aligned} 3 \times 4 = 12 \end{aligned}$

The answer is 12.
::答案是12岁

The length of the corresponding side of the second figure is 12 feet.
::第二个数字的相应侧长度为12英尺。

When you have a figure that is larger than the original, you have a scale factor that is greater than one. If you have a figure that is smaller than the original, then you have a scale factor that is less than one or a fraction.
::当数字大于原数时,则比例系数大于一个。如果数字小于原数,则比例系数小于一个或一个分数。

Let’s look at an example.
::让我们举个例子。

A figure has a side length of 5 meters. What would be the corresponding side length of the new figure if the scale factor is $\begin{aligned} \frac{1}{2} \end{aligned}$ ?
::数字的边长为5米。如果比额表系数为12,新数字的相应边长是多少?

To figure this out, you have to take the given length of the first figure and multiply it by one-half. Remember multiplying by one-half is the same as dividing by 2. This will give you the corresponding length of the second figure.
::要弄清楚这一点, 您需要将第一个图的给定长度乘以一半。记住乘以一半与除以 2相同。这将给您第二个图的对应长度。

$\begin{aligned} 5 \times \frac{1}{2} = \frac{5}{2} \end{aligned}$

The answer is $\begin{aligned} \frac{5}{2} \end{aligned}$ .
::答案是52岁

The length of the corresponding side of the new figure is $\begin{aligned} \frac{5}{2} \end{aligned}$ or 2.5 meters.
::新数字的相应侧长为52米或2.5米。

Now that you understand dilations, you should be able to work with them on the coordinate plane . Once again, you will be using coordinate notation to describe the different dilations that are created on the coordinate plane.
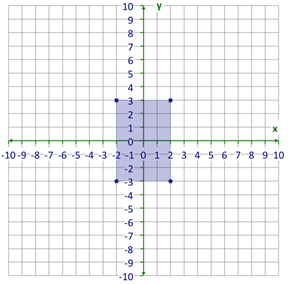
::既然您了解了方位变相, 您应该能够与他们一起在坐标平面上工作。再一次, 您将使用协调符号来描述在坐标平面上产生的不同方位变相。

Let’s look at this figure and then see how you can graph the dilation of it.
::让我们看看这个数字, 然后再看看如何绘制它的放大图。

Graphing dilations of geometric figures is actually fairly easy to do when you know the scale factor. You simply multiply both coordinates for each vertex by the scale factor to produce new coordinates.
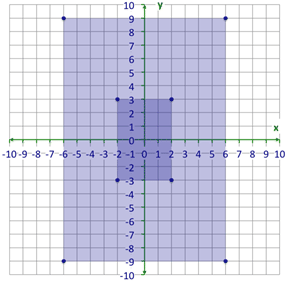
::当您知道比例系数时, 绘制几何数字的方位比值其实相当容易。您只需将每个顶点的两个坐标乘以比例系数即可产生新的坐标。

Suppose you want to make an enlargement of the rectangle above using a scale factor of 3. You need to multiply each coordinate by 3.
::假设您想要使用3 的比值因数扩大上面的矩形, 您需要将每个坐标乘以 3 。

$\begin{aligned} \begin{array}{rcl} (- 2, - 3) \times 3 & = & (- 6, - 9) \\ (- 2, 3) \times 3 & = & (- 6, 9) \\ (2, 3) \times 3 & = & (6, 9) \\ (2, - 3) \times 3 & = & (6, - 9) \end{array} \end{aligned}$

Now you can graph each of these new points on the coordinate plane.
::现在您可以在坐标平面上绘制每个新点的图表。

You can also create a reduction. You create a reduction by dividing each coordinate by the scale factor. This will give you the new measurements of the figure.
::您也可以创建一个缩放。您可以通过将每个坐标除以缩放系数来创建一个缩放。这将为您提供数字的新测量。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about the log cabin model.
::早些时候,有人给了你一个关于木屋模型的问题。

To solve this problem, you begin with the actual dimensions of the log cabin. The log cabin has real world dimensions of $\begin{aligned} 20 \times 40 feet \end{aligned}$ .
::为了解决这个问题,你先从木屋的实际尺寸开始。木屋的真实世界尺寸为20×40英尺。

You are using a scale factor of $\begin{aligned} \frac{1}{16} \end{aligned}$ . That means that the dilation will be a reduction. You need to multiply both dimensions by $\begin{aligned} \frac{1}{16} \end{aligned}$ .
::您正在使用116的比值乘以乘以 116, 也就是说, 推算将会减少。您需要将两个维值乘以 116 。

$\begin{aligned} \begin{array}{rcl} 20 \times \frac{1}{16} & = & 1.25 \\ 40 \times \frac{1}{16} & = & 2.5 \end{array} \end{aligned}$

The answers are 1.25 and 2.5.
::答案是1.25和2.5。

The scale model will be 1.25 feet wide and 2.5 feet long.
::规模模型宽1.25英尺,长2.5英尺。

Example 2
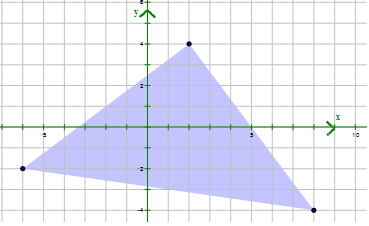
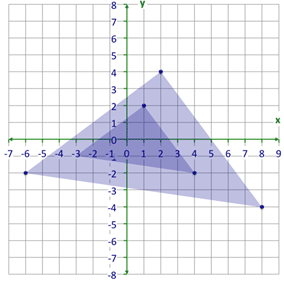
::例2

Graph a reduction of the following figure if the scale factor is $\begin{aligned} \frac{1}{2} \end{aligned}$ .
::如果比额表因数为12,下图为下图的下图。

First, find the coordinates of the original figure.
::首先,找到原始数字的坐标。

$\begin{aligned} (2, 4) \end{aligned}$

$\begin{aligned} (8, - 4) \end{aligned}$

$\begin{aligned} (- 6, - 2) \end{aligned}$

Next, using the scale factor of $\begin{aligned} \frac{1}{2} \end{aligned}$ , find the coordinated of the dilated shape. Remember that multiplying by $\begin{aligned} \frac{1}{2} \end{aligned}$ is the same as dividing by 2.
::使用 12 的缩放系数 12 , 找到膨胀形状的坐标。记住乘以 12 等于以 2 除以 2 。

$\begin{aligned} \begin{array}{rcl} (2, 4) \div 2 & = & (1, 2) \\ (8, - 4) \div 2 & = & (4, - 2) \\ (- 6, - 2) \div 2 & = & (- 3, - 1) \end{array} \end{aligned}$

Then, graph the new dilated shape.
::然后绘制新的膨胀形状图。

Example 3
::例3

A quadrilateral with side measures of 6, 15, 27, and 30 is to be dilated using a scale factor of $\begin{aligned} \frac{1}{3} \end{aligned}$ .
::附带措施为6、15、27和30的四边形将使用13的比额表因数扩大。

Multiply each side measure by $\begin{aligned} \frac{1}{3} \end{aligned}$ .
::乘以每边测量乘以13。

$\begin{aligned} \begin{array}{rcl} 6 \times \frac{1}{3} & = & 2 \\ 15 \times \frac{1}{3} & = & 5 \\ 27 \times \frac{1}{3} & = & 9 \\ 30 \times \frac{1}{3} & = & 10 \end{array} \end{aligned}$

The answer is 2, 5, 9, and 10.
::答案是2,5,9,10。

The new side measures of the dilated quadrilateral are 2, 5, 9, and 10 respectively.
::扩大四边形的新方措施分别为2、5、9和10。

Example 4
::例4

A quadrilateral with side measures of 6, 15, 27, and 30 is to be dilated using a scale factor of $\begin{aligned} \frac{1}{2} \end{aligned}$ .
::附带措施为6、15、27和30的四边形将使用比例系数12放大。

Multiply each side measure by $\begin{aligned} \frac{1}{2} \end{aligned}$ .
::乘以每边测量乘以 12 。

$\begin{aligned} \begin{array}{rcl} 6 \times \frac{1}{2} & = & 3 \\ 15 \times \frac{1}{2} & = & 7.5 \\ 27 \times \frac{1}{2} & = & 13.5 \\ 30 \times \frac{1}{2} & = & 15 \end{array} \end{aligned}$

The answer is 3, 7.5, 13.5, and 15.
::答案是3、7.5、13.5和15。

The new measures of the dilated sides of the quadrilateral are 3, 7.5, 13.5 and 15 respectively.
::四边扩大面的新措施分别为3、7.5、13.5和15。

Example 5
::例5

A quadrilateral with side measures of 6, 15, 27, and 30 is to be dilated using a scale factor of 2.
::附带措施为6、15、27和30的四边形将使用2的比额表因数扩大。

Multiply each side measure by 2.
::乘以每边测量乘以 2 。

$\begin{aligned} \begin{array}{rcl} 6 \times 2 & = & 12 \\ 15 \times 2 & = & 20 \\ 27 \times 2 & = & 54 \\ 30 \times 2 & = & 60 \end{array} \end{aligned}$

The answer is 12, 20, 54, and 60.
::答案是12,20,54和60。

The new side lengths of the dilated quadrilateral are 12, 20, 54, and 60 respectively.
::扩大四边形的新侧长分别为12、20、54和60。

Review
::回顾

Use each scale factor to determine the new dimensions of each figure.
::使用每个比额表系数确定每个数字的新维度。

A triangle with side measures of 4, 5, 9 and a scale factor of 2.
::三角形,边度为4、5、9,比例系数为2。

A triangle with side measures of 4, 5, 9 and a scale factor of 3.
::三角形,侧边测量为4、5、9,比例系数为3。

A triangle with side measures of 4, 5, 9 and a scale factor of 4.
::三角形,边度为4,5,9,比例系数为4。

A triangle with side measures of 8, 10, 14 and a scale factor of 2.
::三角形,边度为8、10、14,比例系数为2。

A triangle with side measures of 8, 10, 14 and a scale factor of 4.
::三角形,边度为8、10、14,比例因数为4。

A triangle with side measures of 2, 4, 6 and a scale factor of 2.
::三角形,边度为2、4、6,比例系数为2。

A quadrilateral with side measures of 4, 6, 8, 10 and a scale factor of $\begin{aligned} \frac{1}{2} \end{aligned}$ .
::附带措施为4、6、8、10的四边形和比例系数为12的四边形。

A quadrilateral with side measures of 12, 16, 20, 24 and a scale factor of $\begin{aligned} \frac{1}{4} \end{aligned}$ .
::附带措施为12、16、20、24的四边形和比例系数为14的四边形。

A quadrilateral with side measures of 4, 6, 8, 10 and a scale factor of 2.
::附带措施为4、6、8、10的四边形和比例系数为2的四边形。

A quadrilateral with side measures of 4, 6, 8, 10 and a scale factor of 3.
::附带措施为4、6、8、10的四边形和比例系数为3的四边形。

A quadrilateral with side measures of 4, 6, 8, 10 and a scale factor of 4.
::附带措施为4、6、8、10的四边形和比例系数为4的四边形。

A quadrilateral with side measures of 9, 12, 18, 24 and a scale factor of $\begin{aligned} \frac{1}{3} \end{aligned}$ .
::附带措施为9、12、18、24的四边形和比例系数为13的四边形。

A quadrilateral with side measures of 9, 12, 18, 24 and a scale factor of 2.
::附带措施为9、12、18、24的四边形和比例系数为2的四边形。

A quadrilateral with side measures of 9, 12, 18, 24 and a scale factor of 3.
::附带措施为9、12、18、24的四边形和比例系数为3的四边形。

A quadrilateral with side measures of 8, 12, 16, 24 and a scale factor of $\begin{aligned} \frac{1}{4} \end{aligned}$ .
::附带措施为8、12、16、24的四边形和比例系数为14的四边形。

A quadrilateral with side measures of 9, 12, 18, 24 and a scale factor of $\begin{aligned} \frac{1}{2} \end{aligned}$ .
::附带措施为9、12、18、24的四边形和比例系数为12的四边形。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

Dilations ::关系

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Dilations
::关系

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源