节: 利用毕达哥里神话的对立面 | 7.7 衍生和利用毕达哥里安理论的对立

章节大纲

Brandon has just purchased his first home and is very anxious to plant a flower garden in a triangular section of the backyard. Brandon has inherited a metal fence that his grandfather had made many years ago and he would like to use it in his garden. The fence consists of two pieces that are welded together to form a right angle and another long straight piece. He knows that the pieces of fence will fit in the garden if his triangular garden is a right triangle .
::布兰登刚刚购买了他的第一座房子,非常渴望在后院的三角区种植花园。布兰登继承了他祖父多年前建造的金属围栏,他想在花园里使用它。围栏由两块铁丝网组成,这些铁丝网被焊在一起形成一个正确的角度,另一块长长的直径。他知道,如果他的三角花园是一个正确的三角形,那么围栏的碎片将适合在花园里。

“If only I could use the garden measurements of 29 feet, 20 feet and 29 feet to figure out if my garden space forms a right triangle, then I could use Grandpa’s fence.” he thought to himself.
::“如果我能用29英尺、20英尺和29英尺的花园测量法来弄清楚我的花园空间是否形成一个正确的三角形,那么我就可以用爷爷的栅栏。 ”他自以为是。

In this concept, you will learn to derive and use the converse of the Pythagorean Theorem .
::在这个概念中,你会学会学习如何利用毕达哥里安神话的对立面。

The Converse of the Pythagorean Theorem
::毕达哥里安神话的对立

The states that for a right triangle the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem can be modeled by the equation $\begin{align*}c^2 = a^2 + b^2\end{align*}$ where ‘ $\begin{align*}c\end{align*}$ ’ represents the length of the hypotenuse, ‘ $\begin{align*}a\end{align*}$ ’ represents the length of one leg and ‘ $\begin{align*}b\end{align*}$ ’ represents the length of the other leg.
::声明右三角形的下限长度平方等于其他两边长度平方的和。这个定理可以用方程式 C2=a2+b2 模拟, 方程式的 " c " 表示下限长度, " a " 表示一条腿的长度, " b " 表示另一条腿的长度。

can be used to calculate the length of an unknown side of a right triangle. The Converse of the Pythagorean Theorem states that if the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the angle opposite the longest side is a right angle. A triangle that contains a right angle is a right triangle.
::可用以计算右三角形不明侧的长度。 Pytagorean 理论的反面表示,如果三角形一面的平方长度等于其他两面的平方长度的平方和,那么,最长的对面的角是一个右角。包含右角的三角形是一个右三角形。

Let’s look at the converse of the Pythagorean Theorem in action.
::让我们看看Pytagorean神话的反面。

Determine whether or not the following triangles (which may not be drawn to scale) are right triangles. If the triangle is a right triangle, make any necessary changes to the triangle and draw it correctly.
::确定以下三角形( 不可绘制为缩放) 是否为右三角形。如果三角形是右三角形, 请对三角形做任何必要的更改, 并正确绘制。

Let’s begin with Triangle One.
::让我们从三角一开始。

First, determine the longest side of the triangle.
::首先,确定三角形最长的一面。

The lengths of the sides are 2, 3 and $\begin{align*}\sqrt{5}\end{align*}$ . The length of side $\begin{align*}BC\end{align*}$ is $\begin{align*}\sqrt{5} \approx 2.24 \ units\end{align*}$ . The longest side of the triangle is $\begin{align*}AB\end{align*}$ which will be the hypotenuse of the triangle if $\begin{align*}\triangle ABC\end{align*}$ is a right triangle.
::边的长度是 2 、 3 和 5. 边的 BC 长度是 5 2. 24 个单位。三角形最长的一面是 AB, 如果 ABC 是正确的三角形, 则三角形的下限就是 ABC 。

Next, substitute the values $\begin{align*}\left(2, \sqrt{5}, 3\right)\end{align*}$ for $\begin{align*}(a, b, c)\end{align*}$ respectively into the equation $\begin{align*}c^2 = a^2 + b^2\end{align*}$ .
::其次,将数值(2,5,3)分别替换为(a,b,c),改为c2=a2+b2。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (3)^{2} & = & (2)^{2} + {(\sqrt{5})}^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2 \\ (3)^2 &=& (2)^2 + \left(\sqrt{5}\right)^2 \end{array}\end{align*}$
::c2=a2+b2(3)2=(2)2+(5)2

Next, square each of the terms indicated in the equation.
::接下来,方程中显示的每个条件平方。

$\begin{aligned} \begin{array}{rcl} (3)^{2} & = & (2)^{2} + {(\sqrt{5})}^{2} \\ (3 \times 3) & = & (2 \times 2) + (\sqrt{5} \times \sqrt{5}) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (3)^2 &=& (2)^2 + \left(\sqrt{5}\right)^2 \\ (3 \times 3) &=& (2 \times 2) + \left(\sqrt{5} \times \sqrt{5}\right) \end{array}\end{align*}$

Next, evaluate each of the squares.
::接下来,对每个广场进行评估。

$\begin{aligned} \begin{array}{rcl} (3 \times 3) & = & (2 \times 2) + (\sqrt{5} \times \sqrt{5}) \\ 9 & = & 4 + 5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (3 \times 3) &=& (2 \times 2) + \left(\sqrt{5} \times \sqrt{5}\right) \\ 9 &=& 4 + 5 \end{array}\end{align*}$

Then, simplify the right side of the equation by adding the numbers.
::然后,通过添加数字简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} 9 & = & 4 + 5 \\ 9 & = & 9 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 9 &=& 4 + 5 \\ 9 &=& 9 \end{array}\end{align*}$

Both sides of the equation are equal. The square of the length of one side of the triangle is equal to the sum of the squares of the lengths of the other two sides. Triangle One is a right triangle. The length of $\begin{align*}BC\end{align*}$ should be 3 and the length of $\begin{align*}AB\end{align*}$ should be $\begin{align*}\sqrt{5}\end{align*}$ since the right angle is located at $\begin{align*}C\end{align*}$ .
::等式的两边相等。三角形一面的平方长度等于其他两边平方长度的平方。三角形一是一个右三角。 BC 长度应为 3, AB 长度应为 5, 因为右角位于 C 。

Let’s look at Triangle Two.
::让我们看看三角洲二。

First, determine the longest side of the triangle.
::首先,确定三角形最长的一面。

The lengths of the sides are $\begin{align*}\sqrt{2}, \sqrt{3}\end{align*}$ and 5. The length of side $\begin{align*}AC\end{align*}$ is $\begin{align*}\sqrt{2}\end{align*}$ , approximately 1.41 units in length. The length of side $\begin{align*}BC\end{align*}$ is $\begin{align*}\sqrt{3}\end{align*}$ , approximately 1.73 units in length. The longest side of the triangle is $\begin{align*}AB\end{align*}$ which will be the hypotenuse of the triangle if $\begin{align*}\triangle ABC\end{align*}$ is a right triangle.
::边的长度是2,3和5。侧的AC的长度是2,大约1.41个单位。边的BC的长度是3,大约1.73个单位的长度。三角的最长的一面是AB,如果 ABC 是右三角,则三角的下限将是ABC。

Next, substitute the values $\begin{align*}\left(\sqrt{2}, \sqrt{3}, 5\right)\end{align*}$ for $\begin{align*}(a, b, c)\end{align*}$ respectively into the equation $\begin{align*}c^2 = a^2 + b^2\end{align*}$ .
::其次,将(a,b,c)的数值(2,3,5)分别替换为c2=a2+b2的方程。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (5)^{2} & = & {(\sqrt{2})}^{2} + {(\sqrt{3})}^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2 \\ (5)^2 &=& \left(\sqrt{2}\right)^2 + \left(\sqrt{3}\right)^2 \end{array}\end{align*}$
::c2=a2+b2(5)2=(2)2+(3)2

Next, square each of the terms indicated in the equation.
::接下来,方程中显示的每个条件平方。

$\begin{aligned} \begin{array}{rcl} (5)^{2} & = & {(\sqrt{2})}^{2} + {(\sqrt{3})}^{2} \\ (5 \times 5) & = & (\sqrt{2} \times \sqrt{2}) + (\sqrt{3} \times \sqrt{3}) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (5)^2 &=& \left(\sqrt{2}\right)^2 + \left(\sqrt{3}\right)^2 \\ \left(5 \times 5\right) &=& \left(\sqrt{2} \times \sqrt{2}\right) + \left(\sqrt{3} \times \sqrt{3}\right) \end{array}\end{align*}$

Next, evaluate each of the squares.
::接下来,对每个广场进行评估。

$\begin{aligned} \begin{array}{rcl} (5 \times 5) & = & (\sqrt{2} \times \sqrt{2}) + (\sqrt{3} \times \sqrt{3}) \\ 25 & = & 2 + 3 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (5 \times 5) &=& \left(\sqrt{2} \times \sqrt{2}\right) + \left(\sqrt{3} \times \sqrt{3}\right) \\ 25 &=& 2+3 \end{array}\end{align*}$

Then, simplify the right side of the equation by adding the numbers.
::然后,通过添加数字简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} 25 & = & 2 + 3 \\ 25 & \neq & 5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 25 &=& 2 + 3 \\ 25 & \neq & 5 \end{array}\end{align*}$

Both sides of the equation are not equal. The square of the length of one side of the triangle is NOT equal to the sum of the squares of the lengths of the other two sides. Triangle Two is not a right triangle.
::等式的两边不相等。三角形一面的平方不等于其他两边的平方和。三角形二不是右三角形。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Brandon’s flower garden and his metal fence. He needs to figure out if his garden space is a right triangle. How can Brandon figure this out using the measurements of the space?
::早些时候,布兰登的花园和金属栅栏给您带来了一个问题。他需要弄清楚他的园艺空间是否是右三角。布兰登如何用测量空间的方法来解决这个问题?

First, determine the values for $\begin{align*}(a, b, c)\end{align*}$ of a right triangle using the measurements of 29, 20 and 21 feet.
::首先,使用29、20和21英尺的测量值确定右三角形(a、b、c)的值。

The longest side will represent ‘c’ the hypotenuse.
::最长的一面代表“c”的下限。

$\begin{align*}a = 20\end{align*}$
::a=20

$\begin{align*}b = 21\end{align*}$
::b=21 b=21

$\begin{align*}c = 29 \end{align*}$
::c=29 (c=29)

Next, substitute the given values into the Pythagorean Theorem.
::接下来, 将给定值替换为 Pytagorien 理论。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (29)^{2} & = & (20)^{2} + (21)^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 +b^2 \\ (29)^2 &=& (20)^2 + (21)^2 \end{array}\end{align*}$
::c2=a2+b2(292)=(202)+(21)2

Next, square each of the terms indicated in the equation.
::接下来,方程中显示的每个条件平方。

$\begin{aligned} \begin{array}{rcl} (29)^{2} & = & (20)^{2} + (21)^{2} \\ (29 \times 29) & = & (20 \times 20) + (21 \times 21) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (29)^2 &=& (20)^2 + (21)^2 \\ (29 \times 29) &=& (20 \times 20) + (21 \times 21) \end{array}\end{align*}$

Next, evaluate each of the squares and simplify the equation.
::接下来,对每个方形进行评估,简化方程。

$\begin{aligned} \begin{array}{rcl} (29 \times 29) & = & (20 \times 20) + (21 \times 21) \\ 841 & = & 400 + 441 \\ 841 & = & 841 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (29 \times 29) &=& (20 \times 20) + (21 \times 21) \\ 841 &=& 400 + 441 \\ 841 &=& 841 \end{array}\end{align*}$

The square of the length of one side of the triangle is equal to the sum of the squares of the lengths of the other two sides. The garden is a right triangle.
::三角形一面的平方长度等于其他两面的平方长度之和。花园是一个右三角形。

Brandon can use his Grandpa’s fence for his flower garden.
::布兰登可以使用爷爷的栅栏来种植花园。

Example 2
::例2

Are the set of numbers (5, 8, 10) the lengths of the sides of a right triangle?
::数字组( 5, 8, 10) 是右三角形两侧的长度吗 ?

First, determine the values for each side of the right triangle. The length of the longest side will represent ‘ $\begin{align*}c\end{align*}$ ,’ the hypotenuse. The other two lengths will represent the lengths of the legs ‘ $\begin{align*}a\end{align*}$ ’ and ‘ $\begin{align*}b\end{align*}$ .’
::首先, 确定右三角形每一侧的值。最长边的长度将代表“ c ” 的下限。其他两个长度将代表腿的长度“ a ” 和“ b ” 。

$\begin{align*}a= 5\end{align*}$
::a=5

$\begin{align*}b = 8\end{align*}$
::b=8 (b=8)

$\begin{align*}c = 10\end{align*}$
::c=10 =

Next, substitute the given values into the Pythagorean Theorem.
::接下来, 将给定值替换为 Pytagorien 理论。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (10)^{2} & = & (5)^{2} + (8)^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2 \\ (10)^2 &=& (5)^2 + (8)^2 \end{array}\end{align*}$
::c2=a2+b2(10.2)2=(5)2+(8)2

Next, square each of the terms indicated in the equation.
::接下来,方程中显示的每个条件平方。

$\begin{aligned} \begin{array}{rcl} (10)^{2} & = & (5)^{2} + (8)^{2} \\ (10 \times 10) & = & (5 \times 5) + (8 \times 8) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (10)^2 &=& (5)^2 + (8)^2 \\ (10 \times 10) &=& (5 \times 5) + (8 \times 8) \end{array}\end{align*}$

Next, evaluate each of the squares.
::接下来,对每个广场进行评估。

$\begin{aligned} \begin{array}{rcl} (10 \times 10) & = & (5 \times 5) + (8 \times 8) \\ 100 & = & 25 + 64 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (10 \times 10) &=& (5 \times 5) + (8 \times 8) \\ 100 &=& 25 + 64 \end{array}\end{align*}$

Then, simplify the right side of the equation by adding the numbers.
::然后,通过添加数字简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} 100 & = & 25 + 64 \\ 100 & \neq & 89 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 100 &=& 25 + 64 \\ 100 & \neq & 89 \end{array}\end{align*}$

Both sides of the equation are not equal. The square of the length of one side of the triangle is NOT equal to the sum of the squares of the lengths of the other two sides.
::等式的两边不相等。三角形两侧的平方长度不等于其他两侧的平方长度之和。

The set of numbers (5, 8, 10) are not the lengths of the sides of a right triangle.
::数字组(5、8、10)不是右三角形两侧的长度。

Example 3
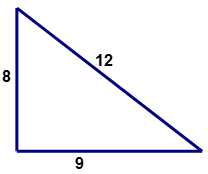
::例3

Is the following triangle (which may or may not be drawn to scale) a right triangle?
::以下三角形( 可能绘制还是不绘制缩放) 是右三角形吗 ?

First, determine the values for $\begin{align*}(a, b, c)\end{align*}$ of a right triangle. The longest side will represent ‘ $\begin{align*}c\end{align*}$ ’ the hypotenuse.
::首先, 确定右三角形( a, b, c) 的值。最长的边将代表“ c” 的下限。

$\begin{align*}a = 8 \end{align*}$
::a=8

$\begin{align*} b = 9\end{align*}$
::b=9 (b=9)

$\begin{align*}c = 12\end{align*}$
::c=12 克=12

Next, substitute the given values into the Pythagorean Theorem.
::接下来, 将给定值替换为 Pytagorien 理论。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (12)^{2} & = & (8)^{2} + (9)^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2 \\ (12)^2 &=& (8)^2 + (9)^2 \end{array}\end{align*}$
::c2=a2+b2(12)2=(8)2+(9)2

Next, square each of the terms indicated in the equation.
::接下来,方程中显示的每个条件平方。

$\begin{aligned} \begin{array}{rcl} (12)^{2} & = & (8)^{2} + (9)^{2} \\ (12 \times 12) & = & (8 \times 8) + (9 \times 9) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (12)^2 &=& (8)^2 + (9)^2 \\ (12 \times 12) &=& (8 \times 8) + (9 \times 9) \end{array}\end{align*}$

Next, evaluate each of the squares.
::接下来,对每个广场进行评估。

$\begin{aligned} \begin{array}{rcl} (12 \times 12) & = & (8 \times 8) + (9 \times 9) \\ 144 & = & 64 + 81 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (12 \times 12) &=& (8 \times 8) + (9 \times 9) \\ 144 &=& 64 + 81 \end{array}\end{align*}$

Then, simplify the right side of the equation by adding the numbers.
::然后,通过添加数字简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} 144 & = & 64 + 81 \\ 144 & \neq & 145 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 144 &=& 64 + 81 \\ 144 & \neq & 145 \end{array}\end{align*}$

Both sides of the equation are not equal. The square of the length of one side of the triangle is NOT equal to the sum of the squares of the lengths of the other two sides. The triangle is not a right triangle.
::等式的两边不相等。三角形一面的平方不等于其他两边的平方和。三角形不是右三角形。

Example 4
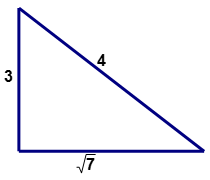
::例4

Is the following triangle (which may or may not be drawn to scale) a right triangle?
::以下三角形( 可能绘制还是不绘制缩放) 是右三角形吗 ?

First, determine the values for $\begin{align*}(a, b, c)\end{align*}$ of a right triangle. The longest side will represent ‘ $\begin{align*}c\end{align*}$ ’ the hypotenuse.
::首先, 确定右三角形( a, b, c) 的值。最长的边将代表“ c” 的下限。

$\begin{align*}\sqrt{7} \approx 2.65\end{align*}$

$\begin{align*}a = 3\end{align*}$
::a=3 =3

$\begin{align*}b = \sqrt{7} \end{align*}$
::b=7 =7

$\begin{align*}c =4\end{align*}$
::c=4个

Next, substitute the given values into the Pythagorean Theorem.
::接下来, 将给定值替换为 Pytagorien 理论。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ (4)^{2} & = & (3)^{2} + {(\sqrt{7})}^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b^2 \\ (4)^2 &=& (3)^2 + \left(\sqrt{7}\right)^2 \end{array}\end{align*}$
::c2=a2+b2(4)2=(3)2+(7)2

Next, square each of the terms indicated in the equation.
::接下来,方程中显示的每个条件平方。

$\begin{aligned} \begin{array}{rcl} (4)^{2} & = & (3)^{2} + {(\sqrt{7})}^{2} \\ (4 \times 4) & = & (3 \times 3) + (\sqrt{7} \times \sqrt{7}) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (4)^2 &=& (3)^2 + \left(\sqrt{7}\right)^2 \\ (4 \times 4) &=& (3 \times 3) + \left(\sqrt{7} \times \sqrt{7}\right) \end{array}\end{align*}$

Next, evaluate each of the squares.
::接下来,对每个广场进行评估。

$\begin{aligned} \begin{array}{rcl} (4 \times 4) & = & (3 \times 3) + (\sqrt{7} \times \sqrt{7}) \\ 16 & = & 9 + 7 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} (4 \times 4) &=& (3 \times 3) + \left(\sqrt{7} \times \sqrt{7}\right) \\ 16 &=& 9 + 7 \end{array}\end{align*}$

Then, simplify the right side of the equation by adding the numbers.
::然后,通过添加数字简化方程式的右侧。

$\begin{aligned} \begin{array}{rcl} 16 & = & 9 + 7 \\ 16 & = & 16 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 16 &=& 9 + 7 \\ 16 &=& 16 \end{array}\end{align*}$

Both sides of the equation are equal. The square of the length of one side of the triangle is equal to the sum of the squares of the lengths of the other two sides. The triangle is a right triangle.
::等式的两边是相等的。三角形一面长度的平方等于其他两面长度的平方和。三角形是一个右三角形。

Review
::回顾

Think about what you have learned about the Pythagorean Theorem and answer true or false for the following questions.
::想想你所学到的关于毕达哥里安神话的教训回答以下的问题回答真或假

1. The Pythagorean Theorem will work for an acute triangle with all 60° angles.
::1. 毕达哥里安定理仪将为所有60度角的急性三角形工作。

2. The Pythagorean Theorem will work for a right triangle.
::2. 毕达哥里安神话将为右三角发挥作用。

3. The Pythagorean Theorem will only work if the triangle is a right triangle.
::3. 唯有三角形是右三角,毕达哥里安理论才有效。

4. The legs of a right triangle are considered the two shorter sides of the right triangle.
::4. 右三角的腿被视为右三角的两边。

5. The hypotenuse is the longest side of a right triangle.
::5. 下限是右三角形最长的一面。

6. The converse of the Pythagorean Theorem is used to find the angle measures of an obtuse triangle.
::6. 利用毕达哥里安定理词的反面来寻找隐形三角形的角度量。

7. A Pythagorean Triple is when you multiply all of the angle measures by three.
::7. 毕达哥伦三重号是将所有角度量乘以3。

8. You can use the Pythagorean Theorem to figure out if the side lengths of a triangle make it a right triangle or not.
::8. 您可以使用毕达哥里安理论来判断三角形的侧长是否为右三角形。

Identify whether or not each of the following values is a Pythagorean Triple. Write yes or no for your answer.
::确定以下每个值是否都是 Pythagorean 3Triple 。请写是或否来回答您的问题。

9. (4, 5, 6)

10. (6, 8, 10)

11. (5, 6, 9)

12. (9, 12, 15)

13. (30, 40, 55)

14. (21, 28, 35)

15. (12, 16, 20).

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

The Converse of the Pythagorean Theorem ::毕达哥里安神话的对立

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

The Converse of the Pythagorean Theorem
::毕达哥里安神话的对立

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源