Section: 45-45-90三角 | 7.11 45-45-90三角

Section outline

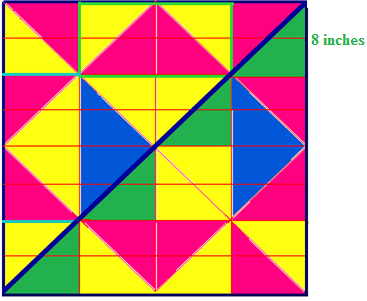
Audrey, has decided to make her classroom look more like a Math class by putting wall paper squares on the doors of the storage cabinets. She has chosen paper that shows squares, and triangles.
::奥德丽,决定让她的教室更像数学课,把壁纸方格放在储藏柜的门上。她选择了显示方形和三角形的纸。

If the length of one of the legs of the $\begin{align*}45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ triangles in the wallpaper is 8 inches in length, then how can Audrey figure out the length of the diagonal of the wallpaper square ?
::如果壁纸上45459090三角形的一条腿长度为8英寸,那么奥德丽如何能找出壁纸方形对角的长度?

In this concept, you will learn to identify isosceles right triangles .
::在此概念中, 您将学会识别右三角形的等离子体。

Isosceles Triangle
::Isosceles 三角形

A triangle that has two sides equal in length and two angles at the base of these sides equal in measure is called an isosceles triangle . If this concept is applied to a right triangle, then the two sides equal in length have to be the legs of the right triangle. Remember the longest side of the right triangle is called the hypotenuse and it is opposite the 90° angle. The two acute angles of a right triangle have a sum of 90° angle. If the legs are equal in length then the two acute angles of the triangle will each measure 45°. The following is an isosceles right triangle .
::两边长度相等的三角形和两角度等量的三角形,称为等距三角形。如果对右三角形应用这个概念,则两边长度相等的三角形必须是右三角形的腿。记住右三角形最长的一面称为下角,对面是90度角。右三角形的两个尖角的角为90度角。如果双腿相等,则三角形的两个尖角将分别测量45度。以下是右三角形的直角。

The angles of an isosceles right triangle will always have the measures of $\begin{align*} 45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ . This triangle is often referred to as a $\begin{align*}45-45-90\end{align*}$ right triangle. The legs of an isosceles right triangle are equal in measure such that $\begin{align*}a = b\end{align*}$ . The length of the hypotenuse can be found using the Pythagorean Theorem .
::直角三角形的角将始终为 454590。此三角形通常被称为 45- 45- 90 右三角形。右三角形的直角的直径相等于 a=b。使用 Pythagorean 理论可以找到下限的长度。

First, determine the values of $\begin{align*}(a, b, c)\end{align*}$ for the Pythagorean Theorem.
::首先,确定毕达哥里安神话的值(a、b、c)。

$\begin{aligned} \begin{array}{rcl} a & = & a \\ b & = & a \\ c & = & ? \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} a &=& a \\ b &=& a \\ c &=& ? \end{array}\end{align*}$
::a=ab=ac=? =ab=ac=ac=? =ab=ac=ac=? =ab=ac=ac=? =ab=ac=ac=? =ab=ac=ac=?

Next, substitute the values for $\begin{align*}(a, b, c)\end{align*}$ into the Pythagorean Theorem.
::其次,将数值(a,b,c)替换为毕达哥里安神话。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & a^{2} + b^{2} \\ c^{2} & = & (a)^{2} + (a)^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& a^2 + b ^2 \\ c^2 &=& (a) ^ 2 + (a)^2 \\ \end{array}\end{align*}$
::c2=a2+b2c2=(a)2+(a)2

Next, perform the indicated squaring on the right side of the equation and simplify.
::下一步,在方程右侧进行标明的对角并简化。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & (a)^{2} + (a)^{2} \\ c^{2} & = & a^{2} + a^{2} \\ c^{2} & = & 2 a^{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& (a) ^ 2 + (a)^2 \\ c^2 &=& a^2 + a ^2 \\ c^2 &=& 2a^2 \\ \end{array}\end{align*}$
::c2=(a)2+(a)2c2=a2+a2+a2c2=2a2

Then, solve for the variable ‘ $\begin{align*}c\end{align*}$ ’ by taking the square root of both sides of the equation. Express the answer as a radical .
::然后,用方程式两侧的平方根解决变量“c”。将答案作为激进表达。

$\begin{aligned} \begin{array}{rcl} c^{2} & = & 2 a^{2} \\ \sqrt{c^{2}} & = & \sqrt{2} \cdot \sqrt{a^{2}} \\ c & = & \sqrt{2} \cdot a \\ c & = & a \sqrt{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c^2 &=& 2a^2 \\ \sqrt{c^2} &=& \sqrt{2} \cdot \sqrt{a^2} \\ c&=& \sqrt{2} \cdot a \\ c&=& a \sqrt{2} \\ \end{array}\end{align*}$
::c2=2a2c2=2a2c2=2a2c=2cac=a2

The answer is $\begin{align*}a \sqrt{2}.\end{align*}$
::答案是a2。

The length of the hypotenuse is $\begin{align*}a \sqrt{2} \ cm\end{align*}$ . Since $\begin{align*}a = b \end{align*}$ the length of the hypotenuse could be expressed as $\begin{align*}b \sqrt{2} \ cm\end{align*}$ .
::下限长度为a2厘米。由于 a=b,下限长度可以以b2厘米表示。

The coefficient ‘ $\begin{align*}a\end{align*}$ ’ in front of $\begin{align*}\sqrt{2} \end{align*}$ is the length of the legs of the given triangle. The length of the hypotenuse of an isosceles right triangle will always equal the product of the leg length and $\begin{align*}\sqrt{2}\end{align*}$ .
::2 前方的系数“a”是给定三角形腿的长度。右三角形等离子体的下限长度总是等于腿长和2的产物。

If a $\begin{align*} 45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ right triangle had a leg length of 5 inches then the length of the hypotenuse would be $\begin{align*}5 \times \sqrt{2} = 5 \sqrt{2}\ in.\end{align*}$
::如果一个4545990右三角形的腿长度为5英寸,则下限长度为5×2=52英寸。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Audrey and the wallpaper squares. She wants to figure out the length of the diagonal of the wallpaper square.
::早些时候,你对奥德丽和墙纸广场产生了问题。她想弄清楚墙纸广场对角的长度。

First, write down what you know.
::首先,写下你知道的

$\begin{aligned} \begin{array}{rcl} a & = & 8 i n = 8 \\ a & = & b = 8 \\ c & = & ? \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} a &=& 8 \ in = \ 8 \\ a &=& b \quad \ = \ 8 \\ c &=& ? \\ \end{array}\end{align*}$
::a=8 = 8a=b = 8c=?

Next, write down an equation to show the relationship between the length of the hypotenuse and the length of a leg.
::接下来,写下一个方程,以显示下限长度和腿长度之间的关系。

$\begin{aligned} c = a \sqrt{2} \end{aligned}$
$\begin{align*}c = a\sqrt{2}\end{align*}$
::c=a2, c=a2, c=a2, c=a2, c=a2, c=c=a2, c=c=a2

Next, substitute what you know into the equation.
::接下来,用你所知道的代替方程式

$\begin{aligned} \begin{array}{rcl} c & = & a \sqrt{2} \\ c & = & 8 \sqrt{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c &=& a\sqrt{2} \\ c &=& 8\sqrt{2} \\ \end{array}\end{align*}$
::c=a2c=82 (千兆克=82)

Remember there are four $\begin{align*}45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ triangles along the diagonal of the wallpaper square.
::记得墙纸广场对角有四个454590三角形。

Then, multiply the value of ‘ $\begin{align*}c\end{align*}$ ’ by the number of triangles.
::然后,将“c”的值乘以三角形数。

$\begin{aligned} \begin{array}{rcl} c & = & 8 \sqrt{2} \\ c & = & 4 (8 \sqrt{2}) \\ c & = & 32 \sqrt{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c &=& 8\sqrt{2} \\ c &=& 4(8\sqrt{2}) \\ c &=& 32 \sqrt{2} \\ \end{array} \end{align*}$ The answer is $\begin{align*}32 \sqrt{2}\end{align*}$ .
::c=82c=4(82)c=322 答案是322

The length of the diagonal of the entire wallpaper square is $\begin{align*}32 \sqrt{2}\end{align*}$ inches.
::整个壁纸广场的对角长度是322英寸。

Example 2
::例2

The length of the leg of the hypotenuse of a $\begin{align*} 45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ triangle is 9 centimeters. What is the length of the hypotenuse?
::454590三角形的顶部长度是9厘米。下限的长度是多少?

First, write down what you know.
::首先,写下你知道的

For the given $\begin{align*}45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ triangle $\begin{align*}a = b = 9\end{align*}$ .
::对于给定的 454590 三角 a=b=9

The length of the hypotenuse ‘ $\begin{align*}c\end{align*}$ ’ is $\begin{align*}a\sqrt{2}\end{align*}$ .
::下限 " c " 长度为 a2。

Then, substitute ‘9’ for ‘ $\begin{align*}a\end{align*}$ ’ to find the length of the hypotenuse.
::以“9”取代“a”,

$\begin{aligned} \begin{array}{rcl} c & = & a \sqrt{2} \\ c & = & 9 \sqrt{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c &=& a\sqrt{2} \\ c &=& 9\sqrt{2} \\ \end{array}\end{align*}$
::c=a2c=92

The answer is $\begin{align*}9 \sqrt{2}.\end{align*}$
::答案是92。

The length of the hypotenuse is $\begin{align*} 9 \sqrt{2} \ cm\end{align*}$ .
::下限长度为92厘米。

Example 3
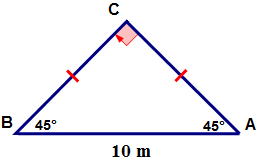
::例3

For the given isosceles, right triangle, find the length of a leg.
::对于给定的等分形, 右三角形, 找到一条腿的长度。

First, write down what you know.
::首先,写下你知道的

$\begin{aligned} \begin{array}{rcl} A C & = & a = ? m \\ a & = & b = ? m \\ c & = & 10 m = 10 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} AC &=& a \ = \ ? \ m \\ a &=& b \ \ = \ ? \ m \\ c &=& 10 \ m \ = \ 10 \\ \end{array}\end{align*}$
::AC=a==? ma=b=? mc=10米=10米=10米

Next, write down an equation to show the relationship between the length of the hypotenuse and the length of a leg.
::接下来,写下一个方程,以显示下限长度和腿长度之间的关系。

$\begin{aligned} c = A C \sqrt{2} \end{aligned}$
$\begin{align*}c= AC \sqrt{2}\end{align*}$ Next, substitute what you know into the equation.
::c=AC2Next,在方程中替换你所知道的东西。

$\begin{aligned} \begin{array}{rcl} c & = & A C \sqrt{2} \\ 10 & = & a \sqrt{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c&=& AC \sqrt{2} \\ 10&=& a \sqrt{2} \\ \end{array}\end{align*}$
::c=AC210=a2

Next, isolate the variable ‘ $\begin{align*}a\end{align*}$ ’ by dividing both sides of the equation by $\begin{align*}\sqrt{2}\end{align*}$ and simplify the equation.
::接下来,通过将方程两侧除以2来孤立变量“a”,并简化方程。

$\begin{aligned} \begin{array}{rcl} 10 & = & a \sqrt{2} \\ \frac{10}{\sqrt{2}} & = & \frac{a \sqrt{2}}{\sqrt{2}} \\ \frac{10}{\sqrt{2}} & = & a \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 10 &=& a\sqrt{2} \\ \frac{10}{\sqrt{2}} &=& \frac{a{\cancel{\sqrt{2}}}} { \cancel{\sqrt{2}}} \\ \frac{10}{\sqrt{2}} &=& a \\ \end{array}\end{align*}$
::10=a 2102=a22102=a

Next, multiply the left side of the denominator by $\begin{align*}\frac{\sqrt{2}}{\sqrt{2}}\end{align*}$ to clear the radical from the denominator.
::接下来,将分母的左侧乘以22 来清除分母中的激进分子。

$\begin{aligned} \begin{array}{rcl} \frac{10}{\sqrt{2}} & = & a \\ \frac{10}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} & = & a \\ \frac{10 \sqrt{2}}{\sqrt{4}} & = & a \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{10}{\sqrt{2}} &=& a \\ \frac{10}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} &=& a \\ \frac{10 \sqrt{2}}{\sqrt{4}} &=& a \\ \end{array}\end{align*}$
::102=a102=22=a1024=a

Then, simplify the left side of the equation to solve for the variable.
::然后简化方程的左侧以解析变量。

$\begin{aligned} \begin{array}{rcl} \frac{10 \sqrt{2}}{\sqrt{4}} & = & a \\ \frac{\overset{5}{10} \sqrt{2}}{2} & = & a \\ 5 \sqrt{2} & = & a \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{10 \sqrt{2}}{\sqrt{4}} &=& a \\ \frac{\overset{5} {\cancel{10}} \sqrt{2} }{{\cancel{2}}} &=& a \\ 5 \sqrt{2} &=& a \\ \end{array}\end{align*}$
::1024=a10522=a52=a

The answer is $\begin{align*}5\sqrt{2}\end{align*}$ .
::答案是52岁

The length of a leg is $\begin{align*}5 \sqrt{2}\end{align*}$ meters.
::腿长52米

Example 4
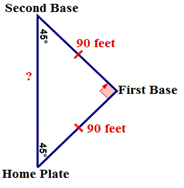
::例4

The distance between the bases of a baseball diamond is 90 feet. If the umpire runs directly from home plate to second base, how far will he have to run? Round the answer to the nearest tenth.
::棒球钻石底部之间的距离是90英尺。如果仲裁人直接从本垒板跑到二垒,那么他还要跑多远? 将答案绕到最近的十分之一。

First, draw and label a diagram to model the problem.
::首先,绘制并标注一个图表来模拟问题。

First, write down what you know.
::首先,写下你知道的

$\begin{aligned} \begin{array}{rcl} A C & = & a = ? m \\ a & = & b = ? m \\ c & = & 10 m = 10 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} AC &=& a \ = \ ? \ m \\ a &=& b \ = \ ? \ m \\ c &=& 10 \ m \ = \ 10 \\ \end{array}\end{align*}$
::AC=a==? ma=b=? mc=10米=10米=10米

Next, write down an equation to show the relationship between the length of the hypotenuse and the length of a leg.
::接下来,写下一个方程,以显示下限长度和腿长度之间的关系。

$\begin{aligned} C = A C \sqrt{2} \end{aligned}$
$\begin{align*}C = AC \sqrt{2}\end{align*}$

::C=AC2

Next, substitute what you know into the equation.
::接下来,用你所知道的代替方程式

$\begin{aligned} \begin{array}{rcl} c & = & A C \sqrt{2} \\ 10 & = & a \sqrt{2} \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c&=& AC \sqrt{2} \\ 10&=& a \sqrt{2} \\ \end{array}\end{align*}$
::c=AC210=a2

Then, using the calculator, perform the operations indicated on the right side of the equation.
::然后,使用计算器,进行方程式右侧指示的操作。

$\begin{aligned} \begin{array}{rcl} c & = & 90 \sqrt{2} \\ c & = & 90 (1.41) \\ c & = & 126.9 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} c&=& 90 \sqrt{2} \\ c &=& 90(1.41) \\ c&=& 126.9 \\ \end{array}\end{align*}$ The answer is 126.9.
::c=902c=90(1.41c=126.9) 答案是126.9。

The umpire runs 126.9 feet.
::裁判长126.9英尺

Review
::回顾

Find the length of the hypotenuse in each of the following $\begin{align*}45 ^\circ - 45 ^\circ - 90 ^\circ\end{align*}$ triangles.
::在以下4545903的三角形中,查找下限的长度。

1. $\begin{align*}\text{Length of each leg} = 5\end{align*}$
::1. 每条腿的长度=5

2. $\begin{align*}\text{Length of each leg} = 4\end{align*}$
::2. 每一腿的长度=4

3. $\begin{align*}\text{Length of each leg} = 6\end{align*}$
::3. 每条腿的长度=6

4. $\begin{align*}\text{Length of each leg} = 3\end{align*}$
::4. 每条腿的长度=3

5. $\begin{align*}\text{Length of each leg} = 7\end{align*}$
::5. 每条腿的长度=7

Use a calculator to figure out the approximate value of each hypotenuse. You may round to the nearest hundredth.
::使用计算器来计算每个下限的大约值。您可以圆到最接近的百位。

6. $\begin{align*} 5\sqrt{2}\end{align*}$

7. $\begin{align*} 4\sqrt{2}\end{align*}$

8. $\begin{align*}6\sqrt{2}\end{align*}$

9. $\begin{align*} 3\sqrt{2}\end{align*}$

10. $\begin{align*}7\sqrt{2}\end{align*}$

11. $\begin{align*} 8\sqrt{2}\end{align*}$

12. $\begin{align*}10\sqrt{2}\end{align*}$

13. $\begin{align*} 13\sqrt{2}\end{align*}$

14. $\begin{align*}21\sqrt{2}\end{align*}$

15. $\begin{align*} 17\sqrt{2}\end{align*}$

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Isosceles Triangle ::Isosceles 三角形

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Isosceles Triangle
::Isosceles 三角形

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)