节: 气瓶量 | 8.11 气瓶体积

章节大纲

Alicia went to the store to buy three cans of soup. Each can has a diameter of 5.4 inches and a height of 6.7 inches. What is the total of soup that Alicia bought?
::Alicia去商店买三罐汤,每个罐子直径5.4英寸,身高6.7英寸。Alicia买的汤总量是多少?

In this concept, you will learn to calculate the volume of different cylinders.
::在这个概念中,你会学会计算不同气瓶的体积。

Volume
::量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量

The volume of a is the measure of how much three-dimensional space it takes up or holds. Volume is measured in cubic units , because you are multiplying three dimensions .
::a 的体积是测量它占用或持有的三维空间的大小。体积以立方单位计量, 因为您正在乘以三个维度。

Let’s look at the formula for the volume of a cylinder : $\begin{align*}V = \pi r^2 h\end{align*}$
::让我们看看气瓶体积的公式:Vr2h

All you need to know is the radius of the circular faces and the height of the cylinder. You simply put these numbers into the formula and solve.
::您只需要知道圆形脸的半径和圆柱体的高度。您只需将这些数字输入公式并解析即可。

Let’s try an example.
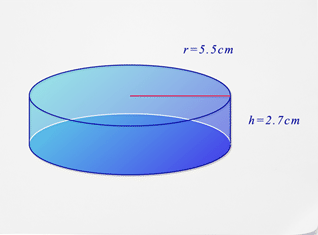
::让我们以身作则。

Find the volume of the cylinder below.
::在下面找到气瓶的体积。

First, substitute what you know into the formula for the volume of a cylinder.
::首先,将你所知道的东西换成气瓶体积的公式

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ V & = & π (5.5)^{2} \times 2.7 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ V &=& \pi (5.5)^2 \times 2.7 \end{array}\end{align*}$
::Vr2hV(5.5)2×2.7

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & π (5.5)^{2} \times 2.7 \\ V & = & π (30.25) \times 2.7 \\ V & = & 256.6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi (5.5)^2 \times 2.7 \\ V &=& \pi (30.25) \times 2.7 \\ V &=& 256.6 \end{array}\end{align*}$
::V(5.5)2x2.7V(30.25)x2.7V=256.6

The answer is 256.6.
::答案是256.6。

The volume is $\begin{align*}256.6 \ cm^3\end{align*}$ .
::卷号为256.6立方厘米。

You can also think about working backwards if you have the volume and one other dimension. Then, you can problem solve to figure out the missing dimension.
::如果有音量和另一个维度,您也可以考虑向后工作。然后,您可以解决问题,找出缺失的维度。

Let’s look at an example.
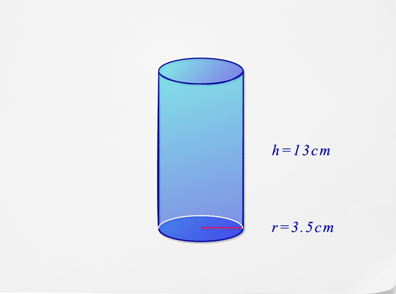
::让我们举个例子。

A cylinder with a radius of 3 inches has a volume of $\begin{align*}140.4 \ \pi\end{align*}$ cubic inches. What is the height of the cylinder?
::半径为3英寸的圆柱体体体积为140.4-立方英寸。圆柱体的高度是多少?

First, substitute what you know into the formula for the volume of a cylinder.
::首先,将你所知道的东西换成气瓶体积的公式

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ 104.4 π & = & π (3)^{2} \times h \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ 104.4 \pi &=& \pi (3)^2 \times h \\ \end{array}\end{align*}$
::Vr2h104. (3)2xh

Next, use algebra to solve for the height, $\begin{align*}h\end{align*}$ .
::下一个,使用代数解析高度,h。

$\begin{aligned} \begin{array}{rcl} 140.4 π & = & π (3)^{2} \times h \\ 140.4 π & = & π (9) \times h \\ \frac{140.4 π}{9 π} & = & \frac{9 π \times h}{9 π} \\ h & = & 15.6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 140.4 \pi &=& \pi(3)^2 \times h \\ 140.4 \pi &=& \pi(9) \times h \\ \frac{140.4 \pi}{9 \pi} &=& \frac{9 \pi \times h}{9 \pi} \\ h &=& 15.6 \end{array}\end{align*}$
::140.4(3)2×h140.4(9)×h140.4999h9h=15.6

The answer is 15.6.
::答案是15.6。

The height is 15 in.
::高度是15英寸。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about Alicia and her soup?
::早些时候,你对Alicia和她的汤有问题吗?

Alicia wants to know the volume of the three cans of soup if each has a diameter of 5.4 inches and a height of 6.7 inches.
::Alicia想知道三罐汤的量如果每罐的直径为5.4英寸高度为6.7英寸的话

First, find the radius of the cylinder. Remember the radius is half the diameter.
::首先,找到圆柱体的半径,记住半径是直径的一半。

$\begin{aligned} \begin{array}{rcl} r & = & \frac{d}{2} \\ r & = & \frac{5.4}{2} \\ r & = & 2.7 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} r &=& \frac{d}{2} \\ r &=& \frac{5.4}{2} \\ r &=& 2.7 \end{array}\end{align*}$
::= rd2r= 5.42r= 2.7

Next, substitute what you know into the formula for the volume of a cylinder.
::接下来,将您所知道的替换为气瓶体积的公式。

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ V & = & π (2.7)^{2} \times 6.7 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ V &=& \pi (2.7)^2 \times 6.7 \end{array}\end{align*}$
::Vr2hV(2.7)2×6.7

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & π (2.7)^{2} \times 6.7 \\ V & = & π (7.29) \times 6.7 \\ V & = & 153.44 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi (2.7)^2 \times 6.7 \\ V &=& \pi (7.29) \times 6.7 \\ V &=& 153.44 \end{array} \end{align*}$
Then, find the total volume for the 3 cans.
::V(2.7)2x6.7V(7.29)x6.7V=153.44 然后,找到3罐的总量。

$\begin{aligned} \begin{array}{rcl} V & = & 3 \times 153.44 \\ V & = & 460.32 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& 3 \times 153.44 \\ V &=& 460.32 \end{array}\end{align*}$
::V=3x153.444V=460.32

The answer is 460.32.
::答案是460.32。

Alicia bought $\begin{align*}460.32 \ in^3\end{align*}$ of soup.
::Alicia买了460.32的汤

Example 2
::例2

A water tank has a radius of 45 feet and a height of 300 feet. How many cubic feet of water will the tank hold when it is full?
::水箱的半径为45英尺,高度为300英尺。水箱满载时将保持多少立方英尺的水?

First, substitute what you know into the formula for the volume of a cylinder.
::首先,将你所知道的东西换成气瓶体积的公式

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ V & = & π (45)^{2} \times 300 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ V &=& \pi (45)^2 \times 300 \\ \end{array}\end{align*}$
::Vr2hV(452×300)

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & π (45)^{2} \times 300 \\ V & = & π (2025) \times 300 \\ V & = & 1908517.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi (45)^2 \times 300 \\ V &=& \pi (2025) \times 300 \\ V &=& 1908517.5 \end{array}\end{align*}$
::V(4552)x300V(2025)x300V=1908517.5

The answer is 1,908,517.5.
::答案是1 908 517.5

The volume is $\begin{align*}1,908,517.5 \ ft^3\end{align*}$ .
::体积为1,908,517.5平方英尺。

Example 3
::例3

Find the volume of a cylinder with a radius of 3 inches and a height of 9 inches.
::找到圆柱体的体积,半径为3英寸,高度为9英寸。

First, substitute what you know into the formula for the volume of a cylinder.
::首先,将你所知道的东西换成气瓶体积的公式

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ V & = & π (3)^{2} \times 9 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ V &=& \pi (3)^2 \times 9 \\ \end{array}\end{align*}$
::Vr2hV(3)2x9

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & π (3)^{2} \times 9 \\ V & = & π (9) \times 9 \\ V & = & 254.47 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi (3)^2 \times 9 \\ V &=& \pi (9) \times 9 \\ V &=& 254.47 \end{array}\end{align*}$
::V(3)2x9V(9)x9V=254.47

The answer is 254.47.
::答案是254.47

The volume is $\begin{align*}254.47 \ in^3\end{align*}$ .
::卷号254.47英寸3。

Example 4
::例4

Find the volume of a cylinder with a radius of 2.5 feet and a height of 6 feet.
::找到圆柱体的体积,半径2.5英尺,高度6英尺。

First, substitute what you know into the formula for the volume of a cylinder.
::首先,将你所知道的东西换成气瓶体积的公式

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ V & = & π (2.5)^{2} \times 6 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ V &=& \pi (2.5)^2 \times 6 \\ \end{array}\end{align*}$
::Vr2hV(2.5)2x6

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & π (2.5)^{2} \times 6 \\ V & = & π (6.25) \times 6 \\ V & = & 117.81 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi (2.5)^2 \times 6 \\ V &=& \pi (6.25) \times 6 \\ V &=& 117.81 \end{array}\end{align*}$
::V( 2.5) 2x6V( 6. 25) x6V=117. 81

The answer is 117.81.
::答案是117.81。

The volume is $\begin{align*}117.81 \ ft^3\end{align*}$ .
::卷号为117.81平方英尺。

Example 5
::例5

Find the volume of a cylinder with a diameter of 5 inches and a height of 7 inches.
::找到一个直径为5英寸、高度为7英寸的圆柱体的体积。

First, find the radius of the cylinder. Remember the radius is half the diameter.
::首先,找到圆柱体的半径,记住半径是直径的一半。

$\begin{aligned} \begin{array}{rcl} r & = & \frac{d}{2} \\ r & = & \frac{5}{2} \\ r & = & 2.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} r &=& \frac{d}{2} \\ r &=& \frac{5}{2} \\ r &=& 2.5 \end{array}\end{align*}$
::= rd2r=52r=2.5

Next, substitute what you know into the formula for the volume of a cylinder.
::接下来,将您所知道的替换为气瓶体积的公式。

$\begin{aligned} \begin{array}{rcl} V & = & π r^{2} h \\ V & = & π (2.5)^{2} \times 7 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi r^2 h \\ V &=& \pi(2.5)^2 \times 7 \end{array}\end{align*}$
::Vr2hV(2.5)2x7

Then, use algebra to solve for the volume.
::然后用代数来解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & π (2.5)^{2} \times 7 \\ V & = & π (6.25) \times 7 \\ V & = & 137.44 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \pi(2.5)^2 \times 7 \\ V &=& \pi(6.25) \times 7 \\ V &=& 137.44 \end{array}\end{align*}$
::V(2.5)2x7V(6.25)x7V=137.44

The answer is 137.44.
::答案是137.44。

The volume is $\begin{align*}137.44 \ in^3\end{align*}$ .
::卷号为137.44英寸3。

Review
::回顾

Answer the questions below the diagram.
::回答图表下面的问题。

1. Name the figure pictured above.
::1. 说明上述数字。

2. What is the diameter of the figure?
::2. 数字的直径是多少?

3. What is the radius is the figure?
::3. 数字的半径是多少?

4. What is the volume of the figure?
::4. 数字的数量是多少?

Find the volume of each cylinder given the radius and height. Use 3.14 to approximate $\begin{align*}\pi\end{align*}$ and round your answers to the nearest hundredths place.
::查找每个圆柱体的体积, 给其半径和高度。使用 3. 14 到大约 ° , 并绕过您的答案到最近的一百个位置。

5. $\begin{align*}r = 4 \ \text{feet}, h = 5 \ \text{feet}\end{align*}$
::5. r=4英尺,h=5英尺

6. $\begin{align*}r = 6 \ cm, h = 8 \ cm\end{align*}$
::6. r=6厘米,h=8厘米

7. $\begin{align*}r = 4.5 \ \text{feet}, h = 5 \ \text{feet}\end{align*}$
::7. r=4.5英尺,h=5英尺

8. $\begin{align*} r = 3.5 \ m, h = 7 \ m\end{align*}$
::8 r=3.5米,h=7米

9. $\begin{align*}r = 13 \ \text{ft}, h = 2 \ \text{ft}\end{align*}$
::9.r=13英尺,h=2英尺

10. $\begin{align*}r = 11 \ m, h = 12 \ m\end{align*}$
::10 r= 11米,h= 12米

11. $\begin{align*} r = 1.5 \ \text{ft}, h = 3 \ \text{ft}\end{align*}$
::11.r=1.5英尺,h=3英尺

12. $\begin{align*}r = 7 \ \text{in}, h = 12 \ \text{in}\end{align*}$
::12 r= 7 英寸,h= 12 英寸

13. $\begin{align*}r = 8 \ cm, h = 11 \ cm\end{align*}$
::13.r=8厘米,h=11厘米

14. $\begin{align*}r = 5 \ m, h = 9 \ m\end{align*}$
::14 r=5米,h=9米

15. $\begin{align*}r = 4.5 \ \text{ft}, h = 6 \ \text{ft}\end{align*}$
::15. r=4.5英尺,h=6英尺

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)