节: 锥体量 | 8.13 锥体量

章节大纲

Sam and Jean have opened a small ice cream stand. They have two different sized cones they sell. A small is $\begin{align*}4^{\prime \prime}\end{align*}$ in diameter and $\begin{align*}4^{\prime \prime}\end{align*}$ in length. A large is $\begin{align*}5^{\prime \prime}\end{align*}$ in diameter and $\begin{align*}6^{\prime \prime}\end{align*}$ in length. Sam wants to charge twice as much for the larger cone because he says that the large cone has twice the . Is he correct?
::Sam和Jean开了一个小型的冰淇淋摊。他们卖的是两个不同大小的圆锥。一个小的直径是4,一个长4。一个大的直径是5,另一个长6。Sam想为更大的圆锥加两倍的价钱,因为他说大的圆锥是它的两倍。他正确吗?

In this concept, you will learn to calculate the volume of cones and truncated cones.
::在这个概念中,你会学会计算锥体和短尾锥体的体积。

Volume
::量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量量

Volume is the measure of how much space a three-dimensional figure takes up or holds. Volume is often what you think of when you talk about measuring liquid or liquid capacity. You use unit cubes to represent volume.
::音量是衡量一个三维图的接收或持有空间大小的尺度。音量通常是您谈论测量液体或液体容量时所想到的。您使用单位立方体代表音量。

Cones are unusual because they are so much smaller at the top than they are at their base. A cone has exactly one-third the volume of a cylinder .
::锥体是不寻常的,因为它们在顶部比在底部要小得多。锥体的体积正好是圆柱体体积的三分之一。

Since the base of a cone is a circle , the formula for finding the volume of a cone is:
::由于锥体的底部是一个圆形,找到锥体体体积的公式是:

$\begin{aligned} V = \frac{1}{3} π r^{2} h \end{aligned}$
$\begin{align*}V=\frac{1}{3} \pi r^2 h\end{align*}$
::V=13°r2h

Now you can see that you would find the area of the base, $\begin{align*}\pi r^2\end{align*}$ , multiply it by the height , $\begin{align*}h\end{align*}$ , and then multiply it by one-third or take one-third of the product of the base area and the height.
::现在你可以看到,你会发现基地的面积, °r2, 乘以它的高度, h, 然后乘以它的三分之一, 或者取取基面积和高度的三分之一的产物。

Let’s look at an example.
::让我们举个例子。

What is the volume of the cone below?
::下面的锥形体体积是多少?

First, substitute what you know into the formula for the volume of a cone.
::首先,用你所知道的来代替锥体的体积

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ V & = & \frac{1}{3} π (3.5)^{2} (22) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ V &=& \frac{1}{3} \pi (3.5)^2 (22) \end{array}\end{align*}$
::V=13r2hV=13(3.5)2(22)

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π (3.5)^{2} (22) \\ V & = & \frac{1}{3} π (12.25) (22) \\ V & = & 282.2 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi (3.5)^2 (22) \\ V &=& \frac{1}{3} \pi (12.25) (22) \\ V &=& 282.2 \end{array}\end{align*}$
::V=13-(3.5)2(22)V=13-(12.25)(12.25)(22)V=282.2

The answer is 282.2.
::答案是282.2。

The volume of the cone is $\begin{align*}282.2 \ cm^3\end{align*}$ .
::锥体的体积为282.2厘米3。

The image below shows a truncated cone.
::下面的图像显示一个短短的锥体。

Notice that you have two radii to work with and the height of the truncated cone as well. You can use the following formula to calculate volume of a truncated cone:
::注意您还有两条线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性、性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性线性

$\begin{aligned} V = \frac{1}{3} π (r_{1}^{2} + r_{1} r_{2} + r_{2}^{2}) h \end{aligned}$
$\begin{align*}V=\frac{1}{3} \pi (r_1^2+r_1r_2+r_2^2)h\end{align*}$
::V=13(r12+r1r2+r22)h

Let’s look at an example.
::让我们举个例子。

What is the volume of a truncated cone with a top radius of 2 cm, a bottom radius of 4 cm and a height of 4.5 cm?
::顶半径为2厘米、底半径为4厘米、高度为4.5厘米的短线锥体的体积是多少?

First, substitute what you know into the formula for the volume of a truncated cone.
::首先,用你所知道的代替公式来代替短流锥体的体积。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π (r_{1}^{2} + r_{1} r_{2} + r_{2}^{2}) h \\ V & = & \frac{1}{3} π (2^{2} + 2 \times 4 + 4^{2}) 4.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi (r_{1}^2+r_1r_2+r_2^2)h \\ V &=& \frac{1}{3} \pi (2^2+2 \times 4 + 4^2)4.5 \end{array}\end{align*}$
::V=13(r12+r1r2+r22)hV=13(22+2×4+42)4.5

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π (2^{2} + 2 \times 4 + 4^{2}) 4.5 \\ V & = & \frac{1}{3} π (28) 4.5 \\ V & = & 131.95 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi (2^2+2 \times 4 + 4^2)4.5 \\ V &=& \frac{1}{3} \pi (28)4.5 \\ V &=& 131.95 \end{array}\end{align*}$
::V=13(22+2×4+42)4.5V=13(28)4.5V=131.95

The answer is 131.95.
::答案是131.95。

The volume of the cone is $\begin{align*}131.95 \ cm^3\end{align*}$ .
::锥体的体积为131.95厘米。

Examples
::实例

Example 1
::例1

Ea rlier, you were given a problem about Sam and Jean’s ice cream venture.
::更早之前, 曾有人对Sam和Jean的冰淇淋投资提出疑问。

Sam wants to charge double for the large cone that has a diameter of $\begin{align*}5^{\prime \prime}\end{align*}$ and a height of $\begin{align*}6^{\prime \prime}\end{align*}$ because he says it has double the volume of the small cone with a diameter of $\begin{align*}4^{\prime \prime}\end{align*}$ and a height of $\begin{align*}4^{\prime \prime}\end{align*}$ . Is Sam correct?
::Sam想对直径为5°C和高度为6°C的大型锥体加双倍的电荷,因为他说,小锥体的体积是小锥体的两倍,直径为4°C和高度为4°C。 Sam 正确吗 ?

First, calculate the volume of the large cone.
::首先,计算大锥体的体积。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ V & = & \frac{1}{3} π (5)^{2} (6) \\ V & = & \frac{1}{3} π (25) (6) \\ V & = & 157.1 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ V &=& \frac{1}{3} \pi (5)^2 (6) \\ V &=& \frac{1}{3} \pi (25)(6) \\ V &=& 157.1 \end{array}\end{align*}$
::V=13r2hV=13(5)2(6)V=13(25)(6)V=157.1

Next, calculate the volume of the small cone.
::接下来,计算小锥体的体积。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ V & = & \frac{1}{3} π (4)^{2} (4) \\ V & = & \frac{1}{3} π (16) (4) \\ V & = & 67.0 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ V &=& \frac{1}{3} \pi (4)^2 (4) \\ V &=& \frac{1}{3} \pi (16)(4) \\ V &=& 67.0 \end{array} \end{align*}$
::V=13r2hV=13(4)2(4)V=13(16)(4)V=67.0

Then, divide the volume of the large cone by the volume of the small cone to see if it is twice as big.
::然后,将大锥体的体积除以小锥体的体积,看看它是不是两倍大。

$\begin{aligned} \begin{array}{rcl} \frac{V_{large cone}}{V_{small cone}} & = & \frac{157.1}{67} \\ \frac{V_{large cone}}{V_{small cone}} & = & 2.34 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} \frac{V_{\text{large cone}}}{V_{\text{small cone}}} &=& \frac{157.1}{67} \\ \frac{V_{\text{large cone}}}{V_{\text{small cone}}} &=& 2.34 \end{array} \end{align*}$

The answer is 2.34.
::答案是2.34。

The volume of ice cream in the large cone is 2.34 times the volume of the small cone. Sam is correct about charging twice the price (and could even charge a little more!)
::大锥体中冰淇淋的体积是小锥体体体积的2.34倍。山姆正确地认为要收费两倍于价格(甚至可以多收费一点 ) 。

Example 2
::例2

What is the height of a cone if the radius is 1.6 meters and volume is 20.1 cubic meters?
::如果半径为1.6米,体积为20.1立方米,锥形的高度是什么?

First, substitute what you know into the formula for the volume of the cone.
::首先,用你所知道的来代替锥体的体积

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ 20.1 & = & \frac{1}{3} π (1.6)^{2} h \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ 20.1 &=& \frac{1}{3} \pi (1.6)^2 h \end{array}\end{align*}$
::V=13r2h20.1=13(1.6)2h

Next, use algebra to solve for the height, $\begin{align*}h\end{align*}$ .
::下一个,使用代数解析高度,h。

$\begin{aligned} \begin{array}{rcl} 20.1 & = & \frac{1}{3} π (1.6)^{2} h \\ 20.1 & = & \frac{1}{3} π (2.56) h \\ 20.1 & = & 2.68 h \\ \frac{20.1}{2.68} & = & \frac{2.68 h}{2.68} \\ h & = & 7.5 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} 20.1 &=& \frac{1}{3} \pi (1.6)^2 h \\ 20.1 &=& \frac{1}{3} \pi (2.56) h \\ 20.1 &=& 2.68 h \\ \frac{20.1}{2.68} &=& \frac{2.68 h}{2.68} \\ h &=& 7.5 \end{array}\end{align*}$
::201=131(1.6)2h20.1=13*2(2.56)h20.1=2.68h20.12.68=2.68h2.68h=7.5

The answer is 7.5.
::答案是7.5。

The height of the cone is $\begin{align*}7.5 \ m\end{align*}$ .
::锥体的高度为7.5米。

Example 3
::例3

Find the volume of a cone with a radius of 2 inches and a height of 4 inches.
::找到圆锥体的体积,半径为2英寸,高度为4英寸。

First, substitute what you know into the formula for the volume of a cone.
::首先,用你所知道的来代替锥体的体积

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ V & = & \frac{1}{3} π (2)^{2} (4) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ V &=& \frac{1}{3} \pi (2)^2 (4) \end{array}\end{align*}$
::V=13r2hV=13(2)(2)(4)

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π (2)^{2} (4) \\ V & = & \frac{1}{3} π (4) (4) \\ V & = & 16.76 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi (2)^2 (4) \\ V &=& \frac{1}{3} \pi (4)(4)\\ V &=& 16.76 \end{array}\end{align*}$
::V=13(2)2(4)V=13(4)(4)V=16.76

The answer is 16.76.
::答案是16.76

The volume of the cone is $\begin{align*}16.76 \ in^3\end{align*}$ .
::锥体的体积是16.76英寸3.

Example 4
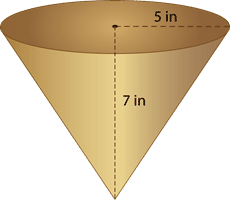
::例4

Find the volume of a cone with a radius of 5 cm and a height of 7 cm.
::查找圆锥体的体积,半径为5厘米,高度为7厘米。

First, substitute what you know into the formula for the volume of a cone.
::首先,用你所知道的来代替锥体的体积

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ V & = & \frac{1}{3} π (5)^{2} (7) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ V &=& \frac{1}{3} \pi (5)^2 (7) \end{array}\end{align*}$

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π (5)^{2} (7) \\ V & = & \frac{1}{3} π (25) (7) \\ V & = & 183.26 \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi (5)^2 (7) \\ V &=& \frac{1}{3} \pi (25)(7) \\ V &=& 183.26 \end{array} \end{align*}$

The answer is 183.26.
::答案是183.26。

The volume of the cone is $\begin{align*}183.26 \ cm^3\end{align*}$ .
::锥体的体积为183.26厘米。

Example 5
::例5

Find the volume of a cone with a radius of 3 m and a height of 8 m.
::查找圆锥体的体积,半径为3米,高度为8米。

First, substitute what you know into the formula for the volume of a cone.
::首先,用你所知道的来代替锥体的体积

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π r^{2} h \\ V & = & \frac{1}{3} π (3)^{2} (8) \end{array} \end{aligned}$
$\begin{align*}\begin{array}{rcl} V &=& \frac{1}{3} \pi r^2 h \\ V &=& \frac{1}{3} \pi (3)^2 (8) \end{array} \end{align*}$

Next, use algebra to solve for the volume.
::接下来,使用代数解析音量。

$\begin{aligned} \begin{array}{rcl} V & = & \frac{1}{3} π (3)^{2} (8) \\ V & = & \frac{1}{3} π (9) (8) \\ V & = & 75.40 \end{array} \end{aligned}$
$\begin{align*} \begin{array}{rcl} V &=& \frac{1}{3} \pi (3)^2 (8) \\ V &=& \frac{1}{3} \pi (9)(8) \\ V &=& 75.40 \end{array} \end{align*}$

The answer is 75.40.
::答案是75.40

The volume of the cone is $\begin{align*}75.40 \ m^3\end{align*}$ .
::锥体的体积为75.40立方米。

Review
::回顾

Answer each of the following questions. Use 3.14 to approximate \pi and round your answers to the nearest hundredths place.
::回答以下每个问题。使用 3. 14 来大约\ pi, 然后将您的答案绕到最近的第 100 个位置。

1. What is the formula for finding the volume of a cone?
::1. 找到锥体体体积的公式是什么?

2. True or false. A truncated cone is a cone without a vertex.
::2. 真实的或假的. 被截断的锥体是没有顶点的锥体。

3. True or false. You can use the same formula to find the volume of a truncated cone as a regular cone.
::3. 真实的或虚假的。您可以使用相同的公式将短流锥体的体积作为普通锥体。

4. What is the diameter of this cone?
::4. 这种锥形的直径是多少?

5. What is the height of the cone?
::5. 锥体的高度是多少?

6. What is the volume of the cone?
::6. 锥体的体积是多少?

7. What is the diameter of this cone?
::7. 这种锥形的直径是多少?

8. What is the height of the cone?
::8. 锥体的高度是多少?

9. What is the volume of the cone?
::9. 锥体的体积是多少?

10. What is the diameter of this cone?
::10. 这种锥形的直径是多少?

11. What is the radius of this cone?
::11. 这个锥形的半径是多少?

12. What is the height of the cone?
::12. 锥体的高度是多少?

13. What is the volume of the cone?
::13. 锥体的体积是多少?

Use what you have learned to solve each of the following problems.
::使用你学到的东西解决以下每一个问题。

14. A cone has a radius of 6 meters and a volume of $\begin{align*}168 \pi\end{align*}$ . What is its height?
::14. 锥体半径为6米,体积为168。

15. The containers of icing for Tina’s cake decorator are cones. Each container has a radius of 2.4 inches and a height of 7 inches. If Tina buys containers of red, yellow, and blue icing, how much icing will she buy?
::15. 蒂娜蛋糕装饰厂的冰柜是锥锥体,每个容器的半径为2.4英寸,高度为7英寸,如果蒂娜购买红色、黄色和蓝色的冰柜,她要买多少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Resources
::资源

章节大纲

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Resources ::资源

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)

Resources
::资源