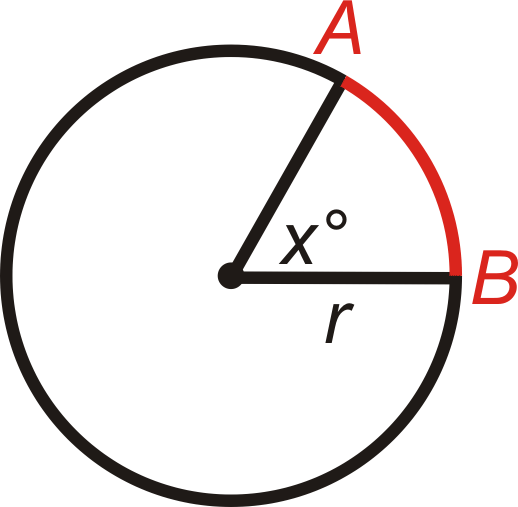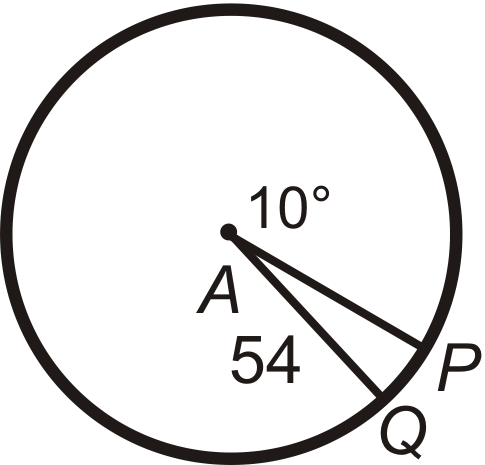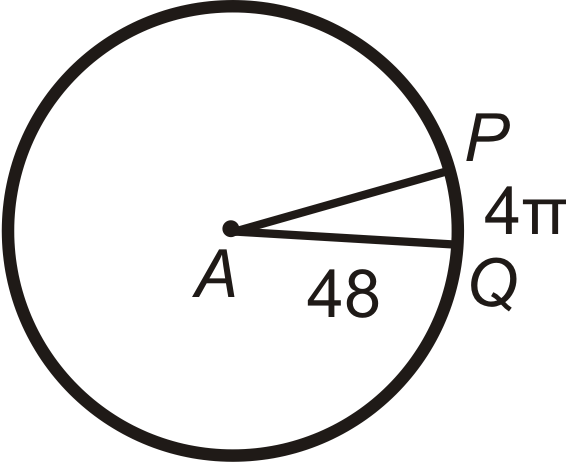弧弧长度

播放段落

Arc Length
::弧弧长度

播放段落

One way to measure arcs is in degrees. This is called the “ arc measure” or “degree measure” (see ). Arcs can also be measured in length, as a portion of the . Arc length is the length of an arc or a portion of a circle’s circumference. The arc length is directly related to the degree arc measure.
::测量弧值的一种方式是度数。 这被称为“ 弧度量” 或“ 度量” (参见 )。 弧值也可以以长度来测量, 作为 的一部分。 弧值长度是弧的长度或圆圈环绕的一部分。 弧值长度与度量直接相关。

播放段落

Arc Length Formula: The length of $\begin{align*}\widehat{AB}=\frac{m \widehat{AB}}{360^\circ} \cdot \pi d\end{align*}$ or $\begin{align*}\frac{m \widehat{AB}}{360^\circ} \cdot 2 \pi r\end{align*}$ .
::弧体长度公式: AB=mAB360d 或 mAB3602r 的长度。

播放段落

What if you were given the angle measure of a circle's arc? How could you find the length of that arc?
::如果给您以圆弧角的角度量呢?你怎么能找到圆弧的长度?

播放段落

Examples
::实例

播放段落

Example 1
::例1

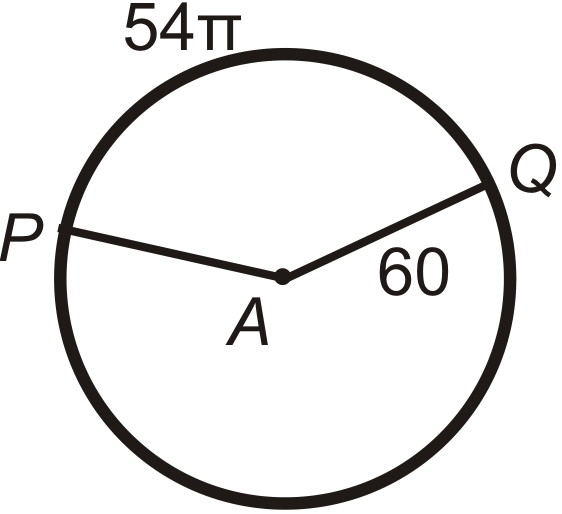
播放段落

Find the arc length of $\begin{align*}\widehat{PQ}\end{align*}$ in $\begin{align*}\bigodot A\end{align*}$ . Leave your answers in terms of $\begin{align*}\pi\end{align*}$ .
::在 A 中查找 PQ 的弧长度。 请将答案保留在 中 。

播放段落

Use the Arc Length formula.
::使用弧长度公式。

播放段落

$$\begin{align*}\widehat{PQ}&=\frac{135}{360}\cdot 2 \pi (12)\\ \widehat{PQ}&=\frac{3}{8}\cdot 24 \pi \\ \widehat{PQ}&=9\pi\end{align*}$$
: -13560-2____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

播放段落

Example 2
::例2

播放段落

A typical large pizza has a diameter of 14 inches and is cut into 8 pieces. Think of the crust as the circumference of the pizza. Find the length of the crust for the entire pizza. Then, find the length of the crust for one piece of pizza if the entire pizza is cut into 8 pieces.
::典型的大比萨饼直径14英寸,切成8块。 将地壳视为披萨环绕。 查找整个比萨饼的地壳长度。 然后, 如果整个比萨饼切成8块, 找到一块比萨饼的地壳长度 。

播放段落

The entire length of the crust, or the circumference of the pizza, is $\begin{align*}14 \pi \approx 44 \ in\end{align*}$ . In $\begin{align*}\frac{1}{8}\end{align*}$ of the pizza, one piece would have $\begin{align*}\frac{44}{8} \approx 5.5\end{align*}$ inches of crust.
::整个地壳的长度,或披萨的环度,是1444英寸。在18英寸的披萨里,一块有4485.5英寸的地壳。

播放段落

Example 3
::例3

播放段落

Find the length of $\begin{align*}\widehat{PQ}\end{align*}$ . Leave your answer in terms of $\begin{align*}\pi\end{align*}$ .
::查找 PQ 的长度。 请将答案保留在 中 。

播放段落

In the picture, the central angle that corresponds with $\begin{align*}\widehat{PQ}\end{align*}$ is $\begin{align*}60^\circ\end{align*}$ . This means that $\begin{align*}m \widehat{PQ}=60^\circ\end{align*}$ . Think of the arc length as a portion of the circumference. There are $\begin{align*}360^\circ\end{align*}$ in a circle , so $\begin{align*}60^\circ\end{align*}$ would be $\begin{align*}\frac{1}{6}\end{align*}$ of that $\begin{align*}\left(\frac{60^\circ}{360^\circ}=\frac{1}{6}\right)\end{align*}$ . Therefore, the length of $\begin{align*}\widehat{PQ}\end{align*}$ is $\begin{align*}\frac{1}{6}\end{align*}$ of the circumference. length of $\begin{align*}\widehat{PQ}=\frac{1}{6} \cdot 2 \pi (9)=3 \pi\end{align*}$ units.
::在图片中,与 PQ 相对应的中心角是 60 。 这意味着 mP 60 。 将弧长度作为环绕的一部分。 圆圈中为 360 , 圆圈中为 16 (60 360 16) 。 因此, P Q 的长度是 16 P 162( 9) = 3 单位。

播放段落

Example 4
::例4

播放段落

The arc length of a circle is $\begin{align*}\widehat{AB}=6 \pi\end{align*}$ and is $\begin{align*}\frac{1}{4}\end{align*}$ the circumference. Find the radius of the circle.
::圆的弧长度为 AB=6, 圆的弧长度为 14。 查找圆的半径 。

播放段落

If $\begin{align*}6 \pi\end{align*}$ is $\begin{align*}\frac{1}{4}\end{align*}$ the circumference, then the total circumference is $\begin{align*}4(6 \pi )=24 \pi\end{align*}$ . To find the radius, plug this into the circumference formula and solve for $\begin{align*}r\end{align*}$ .
::如果 6- 14 是环绕, 则整个环绕为 4( 6 ) = 24 。 要找到半径, 请在环绕公式中插入此值, 并解决 r 。

播放段落

$$\begin{align*}24 \pi &= 2 \pi r\\ 12 \ units &= r\end{align*}$$
::242°r12 单位=r

播放段落

Example 5
::例5

播放段落

Find the measure of the central angle or $\begin{align*}\widehat{PQ}\end{align*}$ .
::查找中角或 QPQ 的测量尺度。

播放段落

Let’s plug in what we know to the Arc Length Formula.
::让我们插入我们所知道的“弧长公式”的插件。

播放段落

$$\begin{align*}15 \pi &= \frac{m \widehat{PQ}}{360^\circ} \cdot 2 \pi (18)\\ 15 &= \frac{m \widehat{PQ}}{10^\circ}\\ 150^\circ &= m \widehat{PQ}\end{align*}$$
:1818)15=mPQ10150PQ

播放段落

Review
::回顾

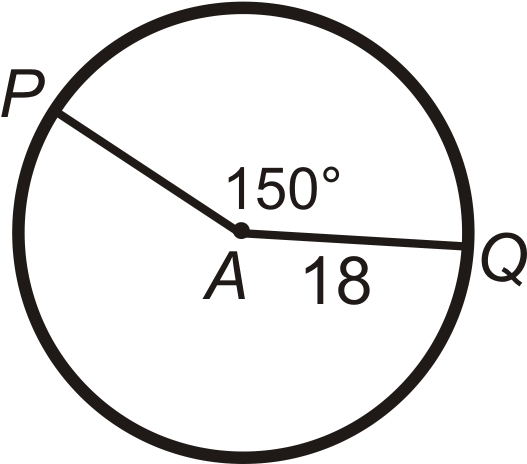
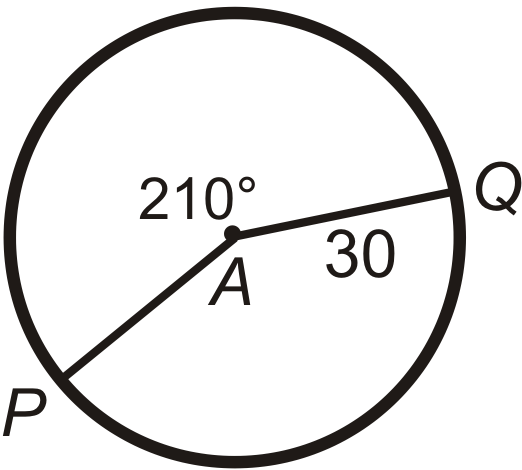
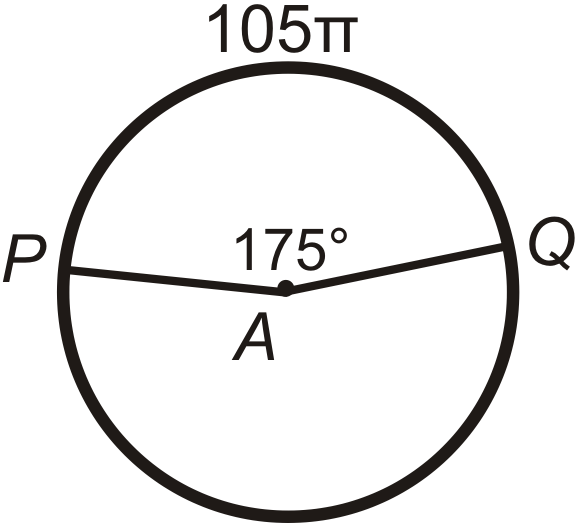
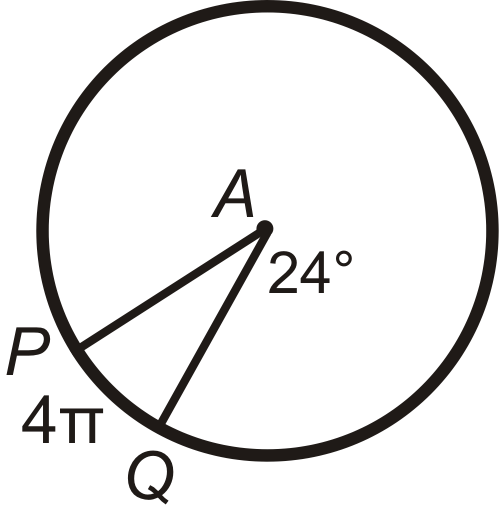
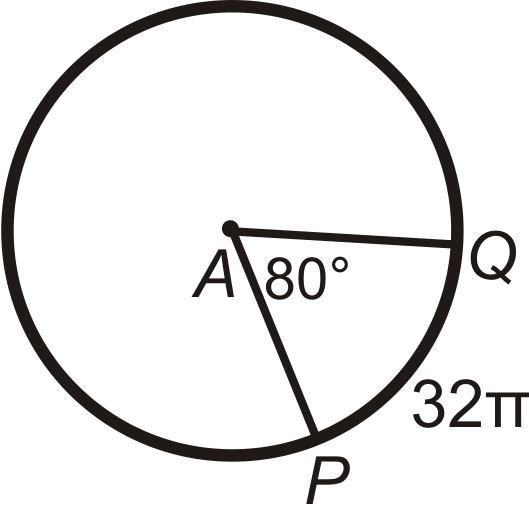
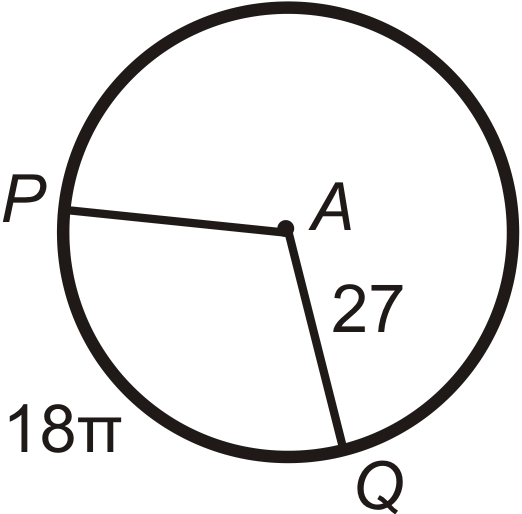
播放段落

Find the arc length of $\begin{align*}\widehat{PQ}\end{align*}$ in $\begin{align*}\bigodot A\end{align*}$ . Leave your answers in terms of $\begin{align*}\pi\end{align*}$ .
::在 A 中查找 PQ 的弧长度。 请将答案保留在 中 。

1. 

2. 

3. 

4. 

播放段落

Find $\begin{align*}PA\end{align*}$ (the radius) in $\begin{align*}\bigodot A\end{align*}$ . Leave your answer in terms of $\begin{align*}\pi\end{align*}$ .
::在 A 中找到 PA( 半径) 。 请保留您的回答 。

5. 

6. 

7. 

播放段落

Find the central angle or $\begin{align*}m \widehat{PQ}\end{align*}$ in $\begin{align*}\bigodot A\end{align*}$ . Round any decimal answers to the nearest tenth.
::在 A 中查找中心角度或 mPQ。 任何十进制回答都以十进制舍入 。

8. 

9. 

10. 

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。