节: 聚面线 | 11.1 圆形 | The Way To Learn

章节大纲

Polyhedrons
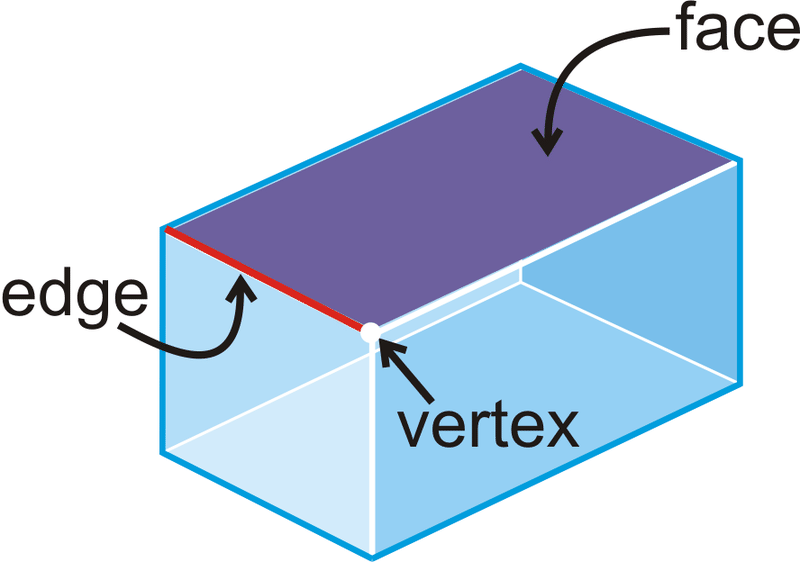
::聚面线

A polyhedron is a 3-dimensional figure that is formed by polygons that enclose a region in space . Each polygon in a polyhedron is a face . The line segment where two faces intersect is an edge . The point of intersection of two edges is a vertex .
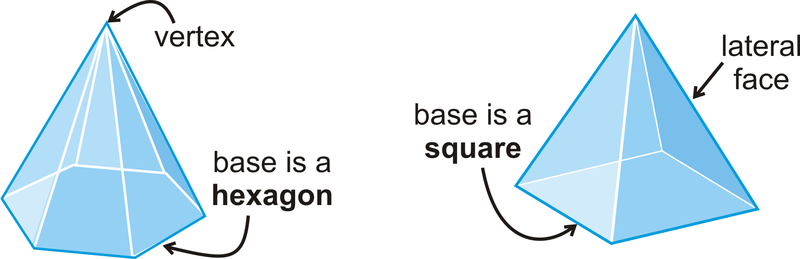
::多面形是一个三维图,由在空间中嵌入一个区域的多边形组成。多面形中每个多边形都是面孔。两面交叉的线条段是边缘。两个边缘的交叉点是一个顶点。

Examples of include a cube, prism , or pyramid . Cones, spheres, and cylinders are not polyhedrons because they have surfaces that are not polygons. The following are more examples of polyhedrons:
::包括立方体、棱晶体或金字塔。锥体、球体和圆柱体不是聚希德龙, 因为它们的表面不是多边形。下面是多希德龙的更多例子:

The number of faces ( $\begin{aligned} F \end{aligned}$ ), vertices ( $\begin{aligned} V \end{aligned}$ ) and edges ( $\begin{aligned} E \end{aligned}$ ) are related in the same way for any polyhedron. Their relationship was discovered by the Swiss mathematician Leonhard Euler, and is called Euler’s Theorem .
::脸部(F)、脊椎(V)和边缘(E)的数量与任何多面形都以同样的方式相关。它们的关系是由瑞士数学家Leonhard Euler发现的,并被称为Euler的理论。

Euler’s Theorem: $\begin{aligned} F + V = E + 2 \end{aligned}$ .
::Euler的理论:F+V=E+2。

\begin{aligned} F a c e s + V e r t i c e s & = E d g e s + 2 \\ 5 + 6 & = 9 + 2 \end{aligned}

::面孔+Vertices=Edges+25+6=9+2

A regular polyhedron is a polyhedron where all the faces are congruent regular polygons. There are only five regular polyhedra, called the Platonic solids.
::普通聚希德龙是一种聚希德龙,所有面孔都是相近的正多边形。只有五个普通的聚希德龙,叫做等离子固体。

Regular Tetrahedron: A 4-faced polyhedron and all the faces are .
::常规德黑兰面板:四面形的多元面板和所有面孔都是。

Cube: A 6-faced polyhedron and all the faces are squares.
::立方体:一个六面体的多面体和所有面孔都是方形的。

Regular Octahedron: An 8-faced polyhedron and all the faces are equilateral triangles.
::普通八面形: 8 面多面形和所有面孔都是等边三角形。

Regular Dodecahedron: A 12-faced polyhedron and all the faces are regular pentagons.
::普通十二面体: 12面的多元面体和所有面孔都是普通的五边形。

Regular Icosahedron: A 20-faced polyhedron and all the faces are equilateral triangles.
::普通的 Icosahedron : 20 面的多元面和所有面孔都是等边三角形。

What if you were given a solid three-dimensional figure, like a carton of ice cream? How could you determine how the faces, vertices, and edges of that figure are related?
::如果给了你一个坚固的三维图,比如一箱冰淇淋呢?你如何确定该图的面孔、脊椎和边缘是如何联系在一起的?

Examples
::实例

Example 1
::例1

Determine if the following solids are polyhedrons. If the solid is a polyhedron, name it and find the number of faces, edges and vertices its has.
::确定以下的固体是否为聚希德龙。如果固态是聚希德龙, 请给它命名, 并找到它拥有的面、边缘和顶点的数量。

The base is a triangle and all the sides are triangles, so this is a triangular pyramid, which is also known as a tetrahedron . There are 4 faces, 6 edges and 4 vertices.
::基座是一个三角形,所有侧面都是三角形, 所以这是一个三角形的金字塔, 也称为阿提拉面。面部有4张, 边缘有6张, 脊椎有4张。

This solid is also a polyhedron. The bases are both pentagons, so it is a pentagonal prism. There are 7 faces, 15 edges, and 10 vertices.
::这颗固体也是多面体。基底是五边形, 所以是五边棱镜。共有7张面, 15个边缘, 10个脊椎。

The bases are circles. Circles are not polygons, so it is not a polyhedron.
::底部是圆圈,圆圈不是多边形,所以不是圆形。

Example 2
::例2

In a six-faced polyhedron, there are 10 edges. How many vertices does the polyhedron have?
::在六面圆面的圆形中,有10个边缘。多面圆形有多少个顶峰?

Solve for $\begin{aligned} V \end{aligned}$ in Euler’s Theorem.
::在尤勒的理论中解决V问题。

\begin{aligned} F + V & = E + 2 \\ 6 + V & = 10 + 2 \\ V & = 6 \end{aligned}

::F+V=E+26+V=10+2V=6

Therefore, there are 6 vertices.
::因此,有6个顶峰。

Example 3
::例3

Markus counts the edges, faces, and vertices of a polyhedron. He comes up with 10 vertices, 5 faces, and 12 edges. Did he make a mistake?
::马库斯计算了多面形的边缘、面部和顶部。他提出了10个顶部、5个脸部和12个边缘。他犯了错吗?

Plug all three numbers into Euler’s Theorem.
::将所有三个数字都插进欧勒的理论中。

\begin{aligned} F + V & = E + 2 \\ 5 + 10 & = 12 + 2 \\ 15 & \neq 14 \end{aligned}

::F+V=E+25+10=12+21514

Because the two sides are not equal, Markus made a mistake.
::因为双方不平等马库斯犯了一个错误

Example 4
::例4

Find the number of faces, vertices, and edges in an octagonal prism.
::在八角棱镜中查找面、顶和边缘的数量。

There are 10 faces and 16 vertices. Use Euler’s Theorem, to solve for $\begin{aligned} E \end{aligned}$ .
::有10张脸和16个顶点。使用欧勒的理论为E解答。

\begin{aligned} F + V & = E + 2 \\ 10 + 16 & = E + 2 \\ 24 & = E \end{aligned}

::F+V=E+210+16=E+224=E

Therefore, there are 24 edges.
::因此,有24个边缘。

Example 5
::例5

A truncated icosahedron is a polyhedron with 12 regular pentagonal faces, 20 regular hexagonal faces, and 90 edges. This icosahedron closely resembles a soccer ball. How many vertices does it have? Explain your reasoning.
::短短的象形面板是一个有12个普通的五角形面孔、20个普通的六角形脸孔和90个边缘的圆形面板。这个象形面板很像一个足球球。它有多少个脊椎? 请解释你的推理。

We can use Euler's Theorem to solve for the number of vertices.
::我们可以用欧勒的理论解答脊椎的数量

\begin{aligned} F + V & = E + 2 \\ 32 + V & = 90 + 2 \\ V & = 60 \end{aligned}

::F+V=E+232+V=90+2V=60

Therefore, it has 60 vertices.
::因此,它有60个顶点。

Review
::回顾

Complete the table using Euler’s Theorem.
::使用 Euler 的定理完成表格。

	*Name*	*Faces*	*Edges*	*Vertices*
1.	Rectangular Prism	6	12
2.	Octagonal Pyramid		16	9
3.	Regular Icosahedron	20		12
4.	Cube		12	8
5.	Triangular Pyramid	4		4
6.	Octahedron	8	12
7.	Heptagonal Prism		21	14
8.	Triangular Prism	5	9

Determine if the following figures are polyhedra. If so, name the figure and find the number of faces, edges, and vertices.
::确定以下数字是否为聚赫德拉。如果是, 请命名该数字并找到面、边缘和顶点的数量。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Polyhedrons ::聚面线

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)