域和范围

播放段落

You and your 3 friends are debating which theater to choose for a trip to the movies on Friday. There are 4 theaters in town, all with different prices for tickets. The most expensive theater charges $12.50 per person, but has stadium seating and a screen 5 stories tall. The cheapest is only $5.50 per ticket, but only plays older movies and is much less comfortable. The other two are between the extremes at $8.50 and $9.75 each.
::你和你的三个朋友正在辩论周五哪个剧院可以选择去看电影。城里有四个剧院,所有剧院的票价都不同。最昂贵的剧院每人收费12.50美元,但体育场座位和屏幕5层高。最便宜的是每张罚单只有5.50美元,但只播放老电影,更不舒适。另外两个在最高区之间,每张价格为8.50美元和9.75美元。

播放段落

If you were to graph the total costs for the 4 of you based on which theater you choose, which values would represent the domain and which the range ?
::如果您要根据您选择的剧院、哪个值代表域和哪个区域来计算你们4人的总成本?

播放段落

Finding Domain and Range
::查找域域和范围

播放段落

Independent Variable, Domain
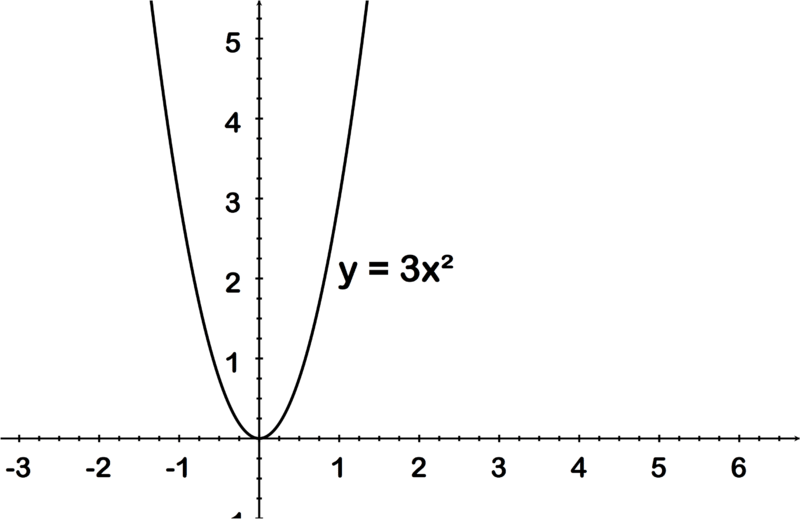
::独立变量, 域

播放段落

The domain of a function is defined as the set of all x values for which the function is defined. For example, the domain of the function $\begin{array}{r}y=3x\end{array}$ is the set of all real numbers, often written as $\begin{array}{r}\mathbb{R}\end{array}$ . This means that x can be any real number . Other functions have restricted domains. For example, the domain of the function $\begin{array}{r}y=\sqrt{x}\end{array}$ is the set of all real numbers greater than or equal to zero. The domain of this function is restricted in this way because the square root of a negative number is not a real number. Therefore , the domain is restricted to non-negative values of x so that the function values will be defined.
::函数的域被定义为函数定义的所有 x 值的一组。 例如, 函数 y= 3x 的域是所有实际数字的一组。 这意味着 x 可以是任何真实数字。 其他函数有限制域。 例如, 函数 y=x 的域是所有实际数字大于或等于零的一组。 此函数的域因负数的平根不是真实数字而受到限制。 因此, 域仅限于 x的非负值, 以便定义函数值 。

播放段落

The variable x is often referred to as the independent variable, while the variable y is referred to as the dependent variable. We talk about x and y this way because the y values of a function depend on what the x values are. That is why we also say that “ y is a function of x .” For example, the value of y in the function y = 3 x depends on what x value we are considering. If x = 4, we can easily determine that y = 3(4) = 12.
::变量 x 通常被称为独立变量,而变量 y 则被称为附属变量。我们这样谈论 x 和 y ,因为函数的 Y 值取决于 x 值。这就是为什么我们还要说“y 是 x 的函数 ” 。例如,函数 y = 3x 中的 y 值取决于我们考虑的 x 值。如果 x = 4,我们很容易确定 y = 3(4) = 12。

播放段落

Dependent Variable, Range
::依赖变量,范围

播放段落

The range of a function is defined as the set of all y values for which a function is defined. Just as we did with domain, we can examine a function and determine its range. Again, it is often helpful to think about what restrictions there might be, and what the graph of the function looks like. Consider for example the function $\begin{array}{r}y=x^2\end{array}$ . The domain of this function is $\begin{array}{r}\mathbb{R}\end{array}$ , all real numbers, but what about the range?
::函数的范围被定义为用于定义函数的所有 y 值的一组值。正如我们对域所做的那样,我们可以检查一个函数并确定其范围。同样,考虑一下可能存在哪些限制,以及函数的图形长什么样子,往往是有益的。例如,考虑函数 y=x2。这个函数的域是 R,所有真实数字,但范围又如何?

播放段落

The range of the function is the set of all real numbers greater than or equal to zero. This is the case because every y value is the square of an x value. If we square positive and negative numbers, the result will always be positive. If x = 0, then y = 0. We can also see the range if we look at a graph of $\begin{array}{r}y=x^2\end{array}$ . Notice below that the y values are all greater than or equal to zero.
::函数的范围是所有实际数字大于或等于零的一组。这是因为每个 y 值是 x 值的平方。如果我们平方正数和负数,结果总是正数。如果 x = 0,那么y = 0。如果我们查看 y =x2 的图形,我们也可以看到范围。下面的注意是 y 值大于或等于 0。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were given a problem about you and 3 friends, who are going to see a movie Friday.
::早些时候,你和3个朋友之间出了点问题, 他们星期五去看电影。

播放段落

If you were to graph the total costs for the 4 of you based on which theater you choose, which values would represent the domain and which the range?
::如果您要根据您选择的剧院、哪个值代表域和哪个区域来计算你们4人的总成本?

播放段落

One function that describes this situation would be: $\begin{array}{r}P(t)=4t\end{array}$ , where $\begin{array}{r}P(t)\end{array}$ would be total Price based on per-ticket price, and it is equal to 4 x ticket price.
::描述这种情况的一个功能是:P(t)=4t,其中P(t)为按每张票价计算的总价格,等于4x票价。

播放段落

In this case, your domain would be: {$5.50, $8.50, $9.75, $12.50} since these are the prices you would input in place of the independent variable , x to get the total price for each theater. The range would be: {$22.00, $34.00, $38.00, $50.00} since these are the output values given by the dependent variable , y .
::在这种情况下,您的域名将是 {5.50,8.50, 8.50, 9.75, 12.50},因为这些是您将投入的价格 来代替独立的变量, x 来获得每个剧院的总价格。范围是 {22.00, 34.00, 38.00, $50.00},因为这些是依附变量y 给出的产出值。

播放段落

Example 2
::例2

播放段落

State the domain of each function.
::说明每项职能的范畴。

播放段落
1. $\begin{array}{r}y=x^2\end{array}$
   ::y=x2 y=x2

播放段落

The domain of this function is the set of all real numbers. There are no restrictions.
::此函数的域是所有实际数字的一组。 没有限制 。

播放段落
2. $\begin{array}{r}\frac{1}{x}\end{array}$
   ::1x 1x

播放段落

The domain of this function is the set of all real numbers except x = 0. The domain is restricted this way because a fraction with denominator zero is undefined .
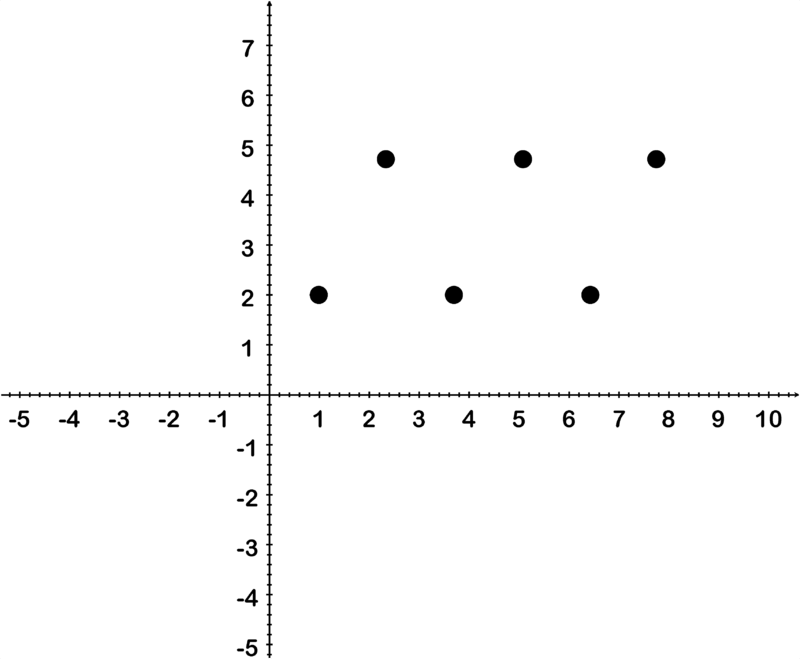
::此函数的域是除 x = 0 外所有实际数字的集合。 此域受此限制, 因为分母为零的分数未定义 。

3. (2, 4), (3, 9), (5, 11)

播放段落

The domain of this function is the set of x values: {2, 3, 5}.
::此函数的域是 x 值组 : {2, 3, 5} 。

播放段落

Example 3
::例3

播放段落

State the of the function $\begin{array}{r}y=\frac{2}{x}\end{array}$ .
::函数 y= 2x 的状态。

播放段落

For this function, we can choose any x value except x = 0, since we cannot divide a number by zero. Therefore the domain of the function is the set of all real numbers except x = 0.
::对于此函数,我们可以选择除 x = 0 以外的任何 x 值,因为我们不能将数字除以 0。因此,该函数的域是除 x = 0 外所有实际数字的集合。

播放段落

The range is also restricted to the non-zero real numbers, but for a different reason. Because the numerator of the fraction is 2, the numerator can never equal zero, so the fraction can never equal zero.
::范围也局限于非零实际数字,但原因不同。由于分数的分子数为2,因此分数永远不能等于零,因此分数永远不能等于零。

播放段落

Example 4
::例4

播放段落

Determine the domain of the function $\begin{array}{r}y=\sqrt{x}\end{array}$ , shown in the graph below.
::确定函数 y=x 的域, 如下图所示 。

播放段落

First consider what restrictions there might be and then look at the graph. We can see that $\begin{array}{r}y=\sqrt{x}\end{array}$ has a domain of all real numbers greater than or equal to zero because the graph only exists for x values that are positive, since there are no real square roots of negative numbers.
::首先考虑可能存在哪些限制, 然后看看图表。 我们可以看到 y=x 拥有一个所有实际数字大于或等于零的域, 因为图中只有正的 x 值存在, 因为没有负数的实际平方根 。

播放段落

Example 5
::例5

播放段落

Give an example of a function for which the domain and range are equivalent to each other.
::举一个例子说明一个函数,其中域和范围彼此等同。

播放段落

Answers will vary. $\begin{array}{r}y=x\end{array}$ is an example.
::答案会有所不同。 Y=x 就是一个例子。

播放段落

Review
::回顾

播放段落

Determine the domain and the range of the relations.
::确定关系的域和范围。

播放段落
1. Relation: {(0,4), (3, 20), (90, 33)}
   ::关系:{(0,4),(3,20),(90,33)}
播放段落
2. Relation: {(3, -4), (6, 37) , (10, -10), (-31, 2)}
   ::关系:{(3,4,6,37),(10,10),(31,2)}
播放段落
3. Tina’s car travels about 30 miles on one gallon of gas. She has between 10 and 12 gallons of gas in the tank. Find the domain and range of the function to calculate how far she can drive.
   ::蒂娜的汽车在一加仑的气体上行驶约30英里。 她的油箱里有10到12加仑的气体。 找到功能的域域和范围来计算她能开多远。
播放段落
4. Joe and three of his friends plan on going bowling and plan on bowling one or two games each. Each game costs $2.75. Find the domain and range of the function calculating the cost of the trip.
   ::乔和他的三个朋友计划去打保龄球 并计划每人打一两场保龄球 每场比赛要花2.75美元 找出计算行程成本的功能的域域和范围
播放段落
5. Bob had a summer job that paid $10.00 per hour and he worked between 20-25 hours every week. His weekly salary can be modeled by the equation S = 10h, where S is his weekly salary and h is the number of hours he worked per week. What is the independent variable for this problem? Describe the domain and range for this problem.
   ::Bob的暑期工作是每小时10.00美元,每周工作20-25小时,每周工资可以S=10小时等式制成,S是每周工资,h是每周工作时数。这个问题的独立变量是什么?描述这一问题的域和范围。
播放段落
6. What does each value in the ordered pair (20, 200) mean in context of the previous problem?
   ::订货配对(20,200)中的每个值在前一个问题中意味着什么?
播放段落
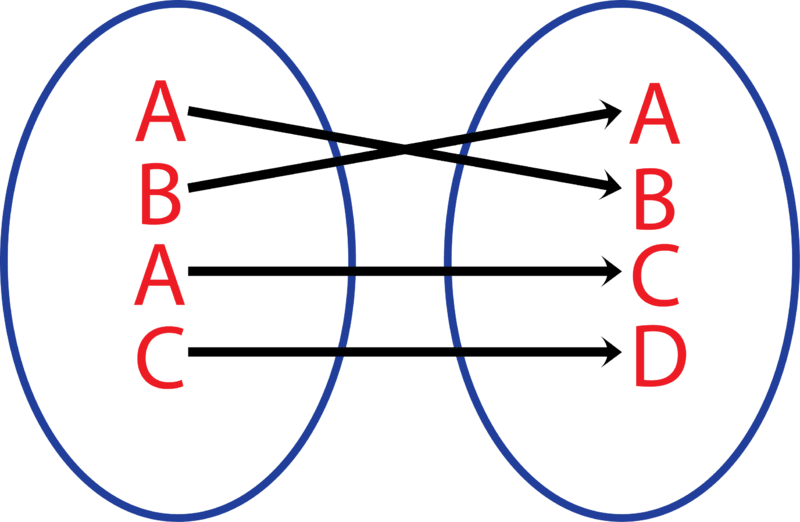
7. Which group of students represents the domain, and which the range, in these ordered pairs? (Jim, Kitty), (Joe, Betty), (Brian, Alice), (Jesus, Anissa), (Ken, Kelli)
   ::这些定购的对子中,哪一组学生代表域名和范围? (吉姆、凯蒂、乔、贝蒂、布里安、爱丽丝、耶稣、阿尼萨、肯、凯利)

播放段落

State the domain and range:
::国家域和范围:

播放段落
8. $\begin{array}{r}y=|x|\end{array}$
   ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
播放段落
9. $\begin{array}{r}x=|y|\end{array}$
   ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
播放段落
10. $\begin{array}{r}y=x^2\end{array}$
    ::y=x2 y=x2
播放段落
11. $\begin{array}{r}x=y^2\end{array}$
    ::x=y2x=y2
12. 
13. 
14. 
15. 

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。