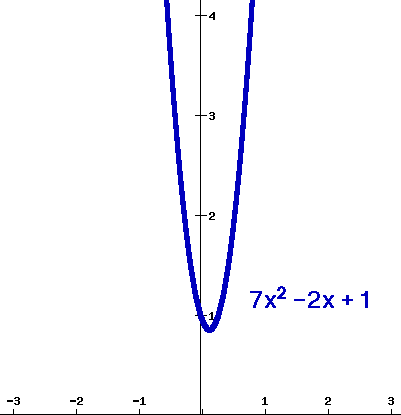节: 函数上的操作 | 1.15 函数上的操作

章节大纲

Just as numbers can be added, subtracted, multiplied, and divided, so too can functions. Combining functions in this way can often have surprising results, as the resultant function may not have a graph that appears similar to that of either input function's graph.
::正如数字可以添加、减、乘、除,函数也可以。这样组合函数往往会产生出人意料的结果,因为由此产生的函数可能没有看上去与任一输入函数图表相似的图表。

How can you tell, before completing the entire operation and graphing the result, whether the new function is likely to resemble one of the input functions? How do you describe combined functions without a graph?
::您如何在完成整个操作和绘制结果图之前辨别新函数是否类似于输入函数之一? 您如何描述没有图形的合并函数 ?

Operations on Functions
::函数上的操作

Sums and Differences of Functions
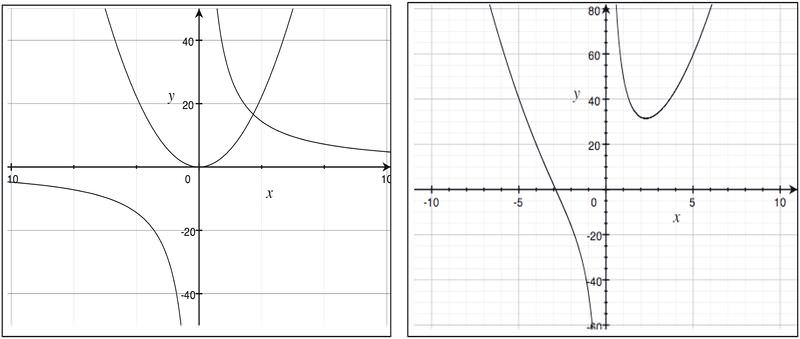
::总和和和职能差异

Consider the function: f ( x ) = 48/ x + 2 x ² .
::考虑函数: f(x) = 48/x + 2x2。

Notice that the equation has two terms :
::注意方程有两个条件:

The first term : 48/ x
::第一任: 48/x

The second term: 2 x ²
::第二个任期:2x2

Therefore we can think of the function f ( x ) as the sum of two other functions:
::因此,我们可以将f(x)职能视为其他两项职能的总和:

The reciprocal function g ( x ) = 48/ x
::互惠函数 g(x) = 48/x

The quadratic function b ( x ) = 2 x ²
::二次函数 b( x) = 2x2

When we add the functions together, we get a new type of graph that resembles both the graphs of g ( x ) and b ( x ):
::当我们一起添加函数时,我们会得到一种新的图表类型,它类似于 g(x) 和 b(x) 的图形:

The graph on the right is f ( x ). The right portion of f ( x ) resembles the parabola b ( x ), but is asymptotic to the y -axis. The left portion of f ( x ) resembles the left side of g ( x ), as both functions are asymptotic to the negative y -axis.
::右侧的图表是 f(x) 。 f(x) 的右部分与 parbola b(x) 相似,但与 y- 轴无关。 f(x) 的左部分与 g(x) 的左侧相似,因为两个函数都与 y- 轴的负值无关。

There are two points to be stressed here: first, that we can add functions together, and second, that the resulting sum may be a different kind of function from the original two.
::这里需要强调两点:第一,我们可以将功能加在一起;第二,由此得出的总和可能与原来的两种功能不同。

The sum or difference of a function is more likely to resemble the original two functions if they are from the same family.
::函数的总和或差数如果来自同一个家庭,则更有可能与原来的两个函数相似。

For example, if two functions from the linear function family are added together, the sum function is also a member of the linear family.
::例如,如果将线性函数家族的两个函数加在一起,总函数也是线性家族的一个成员。

Examples
::实例

Example 1
::例1

Earlier, you were asked if you could discover the trick for identifying when a resultant function graph is likely to resemble the input graphs.
::早些时候,有人询问您能否找到一个诀窍, 来识别何时产生的函数图形可能与输入图形相似。

The sum or difference of a function is more likely to resemble the original two functions if they are from the same family.
::函数的总和或差数如果来自同一个家庭,则更有可能与原来的两个函数相似。

In other words, if you are adding or subtracting two quadratic equations, the result is likely to be quadratic, and have a similar graph.
::换句话说,如果你在增加或减去两个二次方程,结果很可能是二次方程,并有一个类似的图表。

Example 2
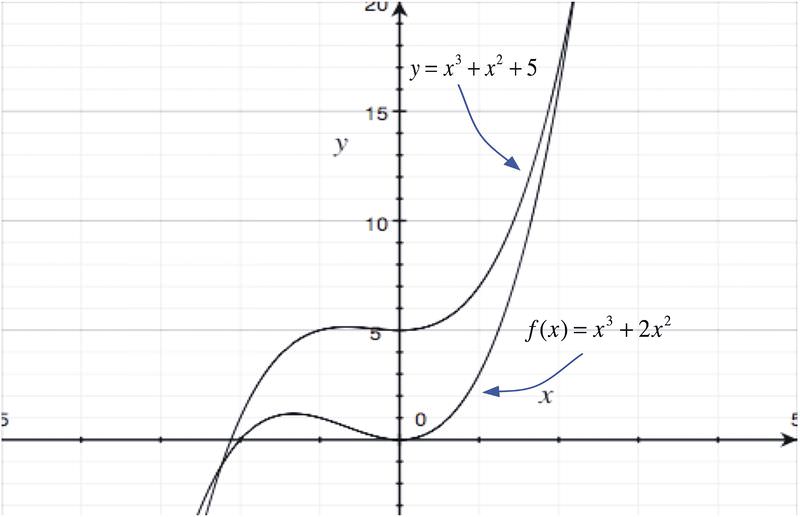
::例2

If f ( x ) = x ³ + 2 x ² and g ( x ) = x ² - 5, what is f - g ? What does the graph look like?
::如果f(x) = x3 + 2x2 和 g(x) = x2 - 5, 什么是 f - g? 图表长什么样 ?

The difference is: f - g = x ³ + 2 x ² - ( x ² - 5) = x ³ + 2 x ² - x ² + 5 = x ³ + x ² + 5
::差别是:f - g = x3 + 2x2 - (x2 - 5) = x3 + 2x2 - x2 + 5 = x3 + x2 + 5

The graph of the new function, along with f ( x ), is shown here:
::在此显示新函数的图形以及f(x) :

Because f ( x ) and the new function y = x ³ + x ² + 5 are both members of the cubic family, they have similar shapes.
::f(x) 和新函数 y = x3 + x2 + 5 是立方体族的成员, 其形状相似。

To recap: When we add or subtract functions, the resulting sum or difference function may be in the same family as one or both of the original functions, or it may be a different type of function. The resultant function is more likely to be in the same family if both of the initial functions are in the same family as each other.
::复述:当我们增加或减去函数时,所产生的总和或差数功能可能与原有函数之一或两个函数相同,也可能是另一种函数。如果最初的函数是在同一家庭中,则后一种函数更有可能在同一家庭中。

Example 3
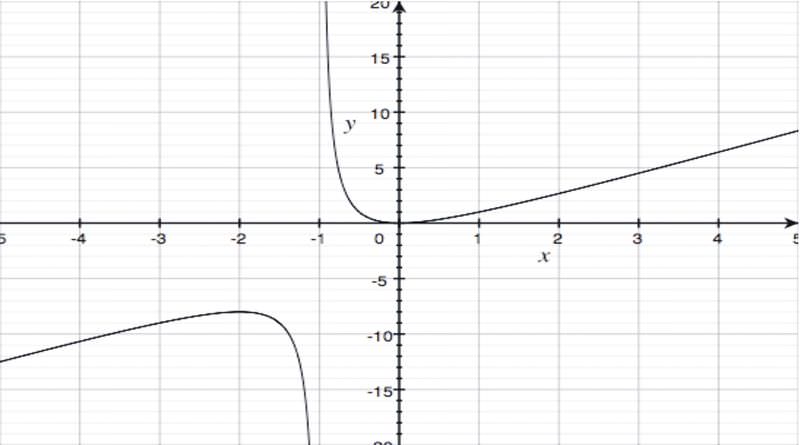
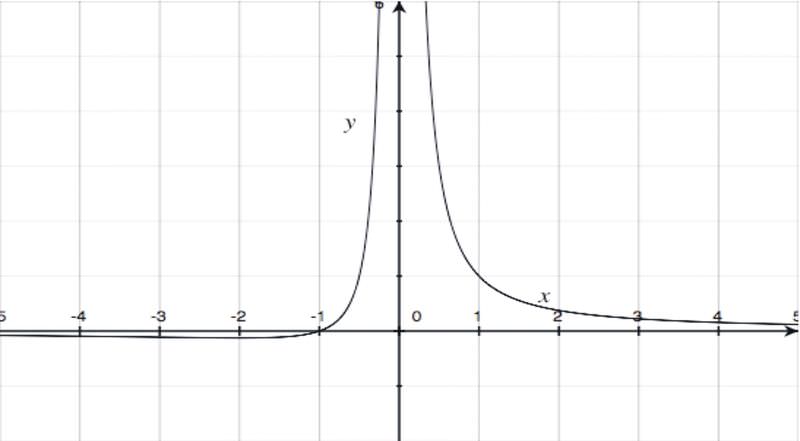
::例3

Given f ( x ) = 2 x ² and g ( x ) = x + 1, find r ( x ) = f ( x )/ g ( x ) and t ( x ) = g ( x )/ f ( x ).
::给定 f(x) = 2x2 和 g(x) = x + 1, 找到 r(x) = f(x) / g(x) 和 t(x) = g(x) / f(x) 。

r ( x ) = f ( x )/ g ( x ) = 2 x ² /( x + 1). This is a rational function , and does not have a horizontal asymptote . It does, however, have a vertical asymptote at x = -1, as the domain excludes x = -1.
::r(x) = f(x) / g(x) = 2x2/(x) + 1 ) 。这是一个合理函数, 并且没有水平等同函数。但是, 它在 x = - 1 时有一个垂直等同函数, 因为域不包括 x = - 1 。

t ( x ) = g ( x )/ f ( x ) = (x + 1)/2x ² . This is also a rational function. This function has a horizontal asymptote at y = 0 (the x -axis), and a vertical asymptote at x = 0 (the y -axis).
::t(x) = g(x) / f(x) = (x + 1)/2x2. 这也是一个理性函数。此函数在 y = 0 (x 轴) 时具有水平等同状态, 在 x = 0 (y 轴) 时具有垂直等同状态。

Notice that the graph of this function crosses its asymptote at (-1, 0), but then as x approaches $\begin{aligned} - \infty \end{aligned}$ , the function values approach 0.
::注意此函数的图形在 (-1, 0) 处交叉其小数点, 但随后作为 x 接近 \\\\\ , 函数值则在 0 处切换。

In general, if we multiply linear and polynomial functions (quadratics, cubics, and other such functions with higher exponents, such as y = x ⁴ + 3 x ² + 2), we will obtain other polynomial functions. If we divide these kinds of functions, we will obtain other polynomial functions, or rational functions.
::一般来说,如果我们乘以线性和多元性函数(quadratics, 立方体, 以及其他具有较高指数的函数, 如 y = x4 + 3x2 + 2) , 我们就会获得其他的多元性函数。如果我们将这些函数分开, 我们就会获得其他多元性函数或理性函数。

Multiplying and dividing other types of functions may result in more complicated graphs.
::乘法和划分其他类型的功能可能会产生更复杂的图表。

Example 4
::例4

Given $\begin{aligned} f (x) = 4 x^{2} - 7 \end{aligned}$ and $\begin{aligned} g (x) = 3 x^{2} - 2 x + 8 \end{aligned}$ , find and graph (use technology) $\begin{aligned} (f + g) (x) \end{aligned}$ .
::给定 f( x) = 4x2-7 和 g( x) = 3x2-2x+8, 查找和图表( 使用技术)( f+g) (x) 。

Step 1: Recall that $\begin{aligned} (f + g) (x) = f (x) + g (x) \end{aligned}$
::第1步:回顾(f+g)(x)=f(x)+g(x)

Step 2: Substitute $\begin{aligned} f (x) + g (x) = (4 x^{2} - 7) + (3 x^{2} - 2 x + 8) \end{aligned}$
::第2步:替代品f(x)+g(x)=(4x2-7)+(3x2-2x+8)

Step 3: Combine like terms $\begin{aligned} (f + g) (x) = 7 x^{2} - 2 x + 1 \end{aligned}$
::第3步:将类似术语(f+g(x)=7x2-2x+1)合并

So our answer is: $\begin{aligned} (f + g) (x) = 7 x^{2} - 2 x + 1 \end{aligned}$
::所以我们的答案是f+g)(x)=7x2-2x+1

The graph of $\begin{aligned} f (x) = 7 x^{2} - 2 x + 1 \end{aligned}$ looks like:
::f( x) = 7x2 - 2x+1 的图形看起来像 :

Example 5
::例5

Multiply the function by the scalar value - if $\begin{aligned} f (x) = 3 x + 10 \end{aligned}$ , find $\begin{aligned} 3 \cdot f (x) \end{aligned}$ .
::将函数乘以 scalar 值 - 如果 f( x) = 3x+10, 则查找 3f( x) 。

To multiply a function by a scalar, multiply each term of the function by the scalar:
::要将函数乘以弧度,函数的每个条件乘以弧度:

Step 1: Substitute: $\begin{aligned} 3 f (x) = 3 (3 x + 10) \end{aligned}$
::第1步:替代:3f(x)=3(3x+10)

Step 2: Distribute: $\begin{aligned} 3 f (x) = 9 x + 30 \end{aligned}$
::步骤2:分配:3f(x)=9x+30

So our answer is: $\begin{aligned} 3 f (x) = 9 x + 30 \end{aligned}$
::所以我们的答案是: 3f( x)=9x+30

Example 6
::例6

Given $\begin{aligned} f (x) = 3 x - 7 \end{aligned}$ and $\begin{aligned} g (x) = 4 x + 6 \end{aligned}$ , find and graph (use technology) $\begin{aligned} (f \cdot g) (x) \end{aligned}$ .
::给定 f( x) = 3x-7 和 g( x) = 4x+6, 查找和图表( 使用技术)( fg) (x) 。

Step 1: Recall that $\begin{aligned} (f \cdot g) (x) = f (x) \cdot g (x) \end{aligned}$
::步骤1:回顾 (fg)(x) = f(x) =g(x)

Step 2: Substitute: $\begin{aligned} f (x) \cdot g (x) = (3 x - 7) (4 x + 6) \end{aligned}$
::第2步:替代物:f(x)g(x)=(3x-7)(4x+6)

Step 3: Distribute (FOIL): $\begin{aligned} (f \cdot g) (x) = 12 x^{2} + 18 x - 28 x - 42 \end{aligned}$
::第3步:分配 (FoIL): (fg(x) = 12x2+18-28x-42)

Step 4: Combine like terms: $\begin{aligned} (f \cdot g) (x) = 12 x^{2} - 10 x - 42 \end{aligned}$
::第4步:将类似术语合并fg)(x)=12x2-10x-42)

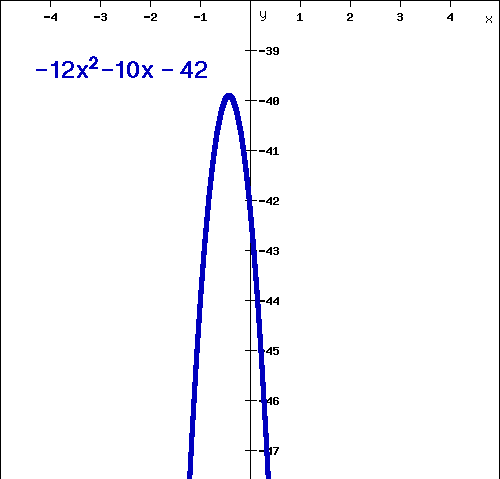
So our answer is: $\begin{aligned} (f \cdot g) (x) = 12 x^{2} - 10 x - 42 \end{aligned}$
::所以我们的答案是: (fg) (x) = 12x2 - 10x-42

The graph of $\begin{aligned} f (x) = 12 x^{2} - 10 x - 42 \end{aligned}$ looks like this:
::f( x) = 12x2 - 10x-42 的图形看起来是这样 :

Review
::回顾

Given $\begin{aligned} f (x) = \frac{x^{3}}{x + 1} \end{aligned}$ and $\begin{aligned} g (x) = x (x + 1) \end{aligned}$ find each of the following:
::给定 f( x) =x3x+1 和 g( x) =x( x+1) , 找到以下各点 :

$\begin{aligned} (f g) (x) = \end{aligned}$
:g)(x)=

$\begin{aligned} (f g) (- 1) = \end{aligned}$
:fg)(-1)=

$\begin{aligned} (\frac{f}{g}) (x) = \end{aligned}$
:g)(x)=

Simplify the following:
::简化如下:

If $\begin{aligned} f (x) = 2 x + 4 \end{aligned}$ and $\begin{aligned} g (x) = 3 x - 7 \end{aligned}$ , find $\begin{aligned} (f + g (x)) \end{aligned}$ .
::如果 f( x) = 2x+4 和 g( x) = 3x-7, 则查找 (f+g( x) )。

If $\begin{aligned} g (x) = \frac{2}{3} x + 12 \end{aligned}$ and $\begin{aligned} h (x) = \frac{1}{4} x + 7 \end{aligned}$ , find $\begin{aligned} (g + h) (x) \end{aligned}$
::如果 g( x) = 23x+12 和 h( x) = 14x+7, 则查找 (g+h) (x)

If $\begin{aligned} f (x) = - 4 x^{2} - 10 \end{aligned}$ and $\begin{aligned} g (x) = 5 x^{2} - 2 x - 3 \end{aligned}$ , find $\begin{aligned} (f + g) (x) \end{aligned}$
::如果 f( x) =4x2 - 10 和 g( x) = 5x2 - 2x - 3, 则查找 (f+g) (x)

If $\begin{aligned} f (x) = 6 x^{2} - 3 x + 5 \end{aligned}$ and $\begin{aligned} g (x) = 4 x^{2} + 5 x - 8 \end{aligned}$ , find $\begin{aligned} (g - f) (x) \end{aligned}$ .
::如果 f( x) = 6x2- 3x+5 和 g( x) = 4x2+5x-8, 则查找 (g- f) (x) 。

If $\begin{aligned} g (x) = 6 x - 8 \end{aligned}$ , find $\begin{aligned} - \frac{3}{2} g (x) \end{aligned}$ .
::如果 g( x) =6x- 8, 则查找 - 32g( x) 。

If $\begin{aligned} g (x) = 2 x^{2} + 3 \end{aligned}$ and $\begin{aligned} h (x) = - 3 x - 6 \end{aligned}$ , find $\begin{aligned} (g \cdot h) (x) \end{aligned}$ .
::如果 g( x) = 2x2+3 和 h( x)\\\\\\\\\\\\\\\6, 找到( g\h) (x) 。

Evaluate:
::评价:

If $\begin{aligned} f (x) = 6 x + 4 \end{aligned}$ and $\begin{aligned} g (x) = - 7 x - 8 \end{aligned}$ , find $\begin{aligned} (f + g) (3) \end{aligned}$ .
::如果f(x)=6x+4和g(x)=7x-8,则查找(f+g)(3)。

If $\begin{aligned} f (x) = \frac{1}{4} x + 3 \end{aligned}$ and $\begin{aligned} h (x) = \frac{3}{2} x + 6 \end{aligned}$ , find $\begin{aligned} (f + h) (12) \end{aligned}$ .
::如果 f( x) = 14x+3 和 h( x) = 32x+6, 则查找 (f+h)( 12) 。

If $\begin{aligned} g (x) = 5 x^{2} - 4 x + 3 \end{aligned}$ and $\begin{aligned} h (x) = 2 x - 7 \end{aligned}$ , find $\begin{aligned} (g - h) (2) \end{aligned}$ .
::如果 g(x) = 5x2-4x+3 和 h(x) = 2x-7, 则查找 (g-h) (2) 。

If $\begin{aligned} g (x) = 4 x^{3} - 3 x \end{aligned}$ find $\begin{aligned} 5 g (6) \end{aligned}$ .
::如果 g(x) = 4x3- 3x 发现 5g(6) 。

If $\begin{aligned} h (x) = | 4 x - 7 | \end{aligned}$ find $\begin{aligned} 2 h (- 5) \end{aligned}$ .
::如果 h( x) 4x- 7 找到 2h( ~ 5) 。

If $\begin{aligned} f (x) = x + 4 \end{aligned}$ and $\begin{aligned} g (x) = 3 x - 6 \end{aligned}$ , find $\begin{aligned} (f \cdot g) (1) \end{aligned}$ .
::如果f(x)=x+4和g(x)=3x-6,则查找(f)g)(1)。

If $\begin{aligned} h (x) = x^{4} \end{aligned}$ and $\begin{aligned} g (x) = x - 12 \end{aligned}$ , find $\begin{aligned} (h \cdot g) (- 2) \end{aligned}$ .
::如果 h(x) =x4 和 g(x) =x- 12, 则查找 g(-2) 。

Try to solve these more challenging problems.
::试着解决这些更具挑战性的问题。

If $\begin{aligned} f (x) = 4 x - 7 \end{aligned}$ , $\begin{aligned} g (x) = 3 x + 18 \end{aligned}$ , and $\begin{aligned} h (x) = - 5 x + 2 \end{aligned}$ , find $\begin{aligned} (f + g - h) (x) \end{aligned}$ .
::如果 f( x) =4x-7, g( x) =3x+18, h( x) =5x+2, 则查找 (f+g-h) (x) 。

If $\begin{aligned} f (x) = 6 x - 8 \end{aligned}$ , $\begin{aligned} g (x) = \frac{1}{2} x \end{aligned}$ , and $\begin{aligned} h (x) = x + 4 \end{aligned}$ , find $\begin{aligned} (f \cdot g \cdot h) (x) \end{aligned}$
::如果 f( x) = 6x - 8, g( x) = 12x, h( x) =x+4, 则查找 (fgh) (x)

If $\begin{aligned} g (x) = 3 x - 7 \end{aligned}$ and $\begin{aligned} (g \cdot h) (x) = 15 x^{2} - 47 x + 28 \end{aligned}$ , find (x)"> $\begin{aligned} (h) (x) \end{aligned}$ .
::如果 g(x) = 3x-7 和 (g) h(x) = 15x2- 47x+28, 请查找 (x) 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Operations on Functions ::函数上的操作

Sums and Differences of Functions ::总和和和职能差异

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Operations on Functions
::函数上的操作

Sums and Differences of Functions
::总和和和职能差异

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)