节: 复数极表 | 4.8 复数极表

章节大纲

can be graphed on a polar graph just like real numbers can. You will discover during this lesson that there are actually a few different ways of doing this.
::可以在极地图上像真实数字一样图形化。您将会在这个课程中发现, 实际上有几种不同的方法来做这个操作。

Polar Form of Complex Numbers
::复数极表

You have learned that rectangular graphs can be put into polar form , and that points in rectangular coordinates can be plotted in the polar coordinate system. In this section you will learn how to do the same process with complex numbers.
::您已经学会了, 矩形图形可以以极形形式出现, 矩形坐标上的点可以在极地坐标系统中绘制。在本节中, 您将学习如何使用复杂数字进行相同的进程。

There are three common forms of complex numbers that you will see when graphing:
::有三种常见的复杂数字形式,您在图形化时可以看到:

In the standard form of: z = a + bi , a complex number z can be graphed using rectangular coordinates ( a , b ). ‘a’ represents the x - coordinate, while ‘b’ represents the y - coordinate.
::标准格式为:z = a + bi, 复数 z 可使用矩形坐标(a, b) 绘制图表。 " a " 表示 x - 坐标,而 " b " 表示 y - 坐标。

The polar form: $\begin{aligned} (r, θ) \end{aligned}$ which we explored in a previous lesson, can also be used to graph a complex number. Recall that you can use x and y to convert between rectangular and polar forms with: $\begin{aligned} r = \sqrt{x^{2} + y^{2}} \end{aligned}$ and $\begin{aligned} tan θ_{r e f} = | \frac{y}{x} | \end{aligned}$ . Unfortunately, there is a problem with using a conversion from rectangular form to polar form like:
::极形 : (r, ) , 我们在前一课中探讨过, 也可以用来绘制一个复数。回顾您可以使用 x 和 y 在矩形和极形之间转换 : r=x2+y2 和 tan refyx 。不幸的是, 使用矩形转换为极形有问题, 比如 :

$\begin{aligned} a + b i \to (r, θ) \end{aligned}$
::a+bi___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

or
::或

$\begin{aligned} - 1 - i \sqrt{3} \to (2, \frac{4 π}{3}) \end{aligned}$
::-1-i3_______________________________________________________________________________________________________________________________________________________________________________________________________________

The problem is that we have lost the i . So, in order to “keep track” of the imaginary part, we can use another form.
::问题是,我们失去了i。所以,为了“追踪”假想的部分,我们可以使用另一种形式。

The third form is trigonometric form . It is often abbreviated as rcisθ , short for: z = r ( c osθ + is inθ), and will be used quite often as you progress. This form comes from the substitutions: x = r θ and y = r θ .
::第三种形式是三角形。通常缩写为 rcis : rcis : z = r( cos + isin) , 并且随着您的进展, 将经常使用。此形式来自替换 : x = r r = y = r = r 。

Using this fact, and sample values of $\begin{aligned} 2 \end{aligned}$ for r and $\begin{aligned} \frac{π}{3} \end{aligned}$ for θ , we can write
::使用这个事实, r 的样本值为 2 , r 的样本值为 #% 3 , 我们可以写入

$\begin{aligned} z = - 1 - i \sqrt{3} = 2 cos \frac{4 π}{3} + 2 i sin \frac{4 π}{3} \end{aligned}$
::1 - i3=2 cs 43+2 I sin 43

Finally, factoring the 2, we get: $\begin{aligned} z = 2 (cos \frac{4 π}{3} + i sin \frac{4 π}{3}) \end{aligned}$
::最后,考虑到2,我们得到:z=2(2cs 43+i sin 43)

Summary of Forms
::形式摘要

The complex number: $\begin{aligned} z = - 1 - \sqrt{3} i \end{aligned}$ , the rectangular point $\begin{aligned} (- 1, - \sqrt{3}) \end{aligned}$ , the polar point: $\begin{aligned} (2, \frac{4 π}{3}) \end{aligned}$ , and $\begin{aligned} 2 (cos \frac{4 π}{3} + i sin \frac{4 π}{3}) \end{aligned}$ or $\begin{aligned} 2 cis (\frac{4 π}{3}) \end{aligned}$ all represent the same number.
::复数 : z1-3i, 矩形点 (-1-3), 极点 (2,43), 和 2( cos 43+i sin 43) 或 2 cis (43) , 均为相同数字。

Steps for Conversion
::转换步骤

To convert from polar to rectangular form, the distance that the point (2, 2) is from the origin can be found by
::要从极向矩形转换成矩形,点(2,2)与源的距离可以由下列方式找到:

$\begin{aligned} d = \sqrt{x^{2} + y^{2}} \end{aligned}$ or $\begin{aligned} \sqrt{2^{2} + 2^{2}} d = \sqrt{8} \end{aligned}$ or $\begin{aligned} 2 \sqrt{2} \end{aligned}$
::d=x2+y2 或 22+22 d=8 或 22

The reference angle (i.e. the corresponding angle in the first quadrant) that the line segment between the point and the origin can be found by
::点与源之间线段的参考角度(即第一个象度中相应的角),可按下列方式查找:

$\begin{aligned} tan θ_{r e f} = | \frac{y}{x} | \end{aligned}$
::现现年日年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年年

for z = 2 + 2 i ,
::z = 2 + 2i,

$\begin{aligned} tan θ_{r e f} = \frac{2}{2} \end{aligned}$
::皮肤 $2$22 $2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$2$s

$\begin{aligned} tan θ_{r e f} = 1. \end{aligned}$
::棕色 ref= 1 。

Since this point is in the first quadrant (both the x and y coordinate are positive) the angle must be 45 ^o or $\begin{aligned} \frac{π}{4} \end{aligned}$ radians.
::由于此点位于第一个象限( x 和 y 坐标均为正) , 角度必须是 45 o 或 4 弧度。

It is also possible that when θ = 1 the angle can be in the third quadrant or $\begin{aligned} \frac{5 π}{4} \end{aligned}$ radians. But this angle will not satisfy the conditions of the problem, since a third quadrant angle must have both $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ as negatives.
::当 = = = 1 时, 角度也可以在第三个象限或 5 4 弧度中。但是, 这个角度无法满足问题的条件, 因为第三个象限角度必须同时有 x 和 y 的负值。

Note: When using $\begin{aligned} tan θ = \frac{y}{x} \end{aligned}$ , you should first consider, the quotient $\begin{aligned} | \frac{y}{x} | \end{aligned}$ and find the first quadrant angle that satisfies this condition. This angle will be called the reference angle, denoted $\begin{aligned} θ_{r e f} \end{aligned}$ . Find the actual angle by analyzing which quadrant the angle must be given the x and y signs.
::注意 : 当使用 tan yx 时, 您应该首先考虑, 商数 , 并找到第一个满足此条件的象方角。这个角度将被称为引用角 , 表示 ref 。通过分析 x 和 y 符号必须给该角度的方位数来查找实际角度。

The complex number 2 + 2 i or (2, 2) in rectangular form has $\begin{aligned} (2 \sqrt{2}, \frac{π}{4}) \end{aligned}$
::2+2i或(2,2,2)的矩形复合体有(22,%4)

Examples
::实例

Example 1
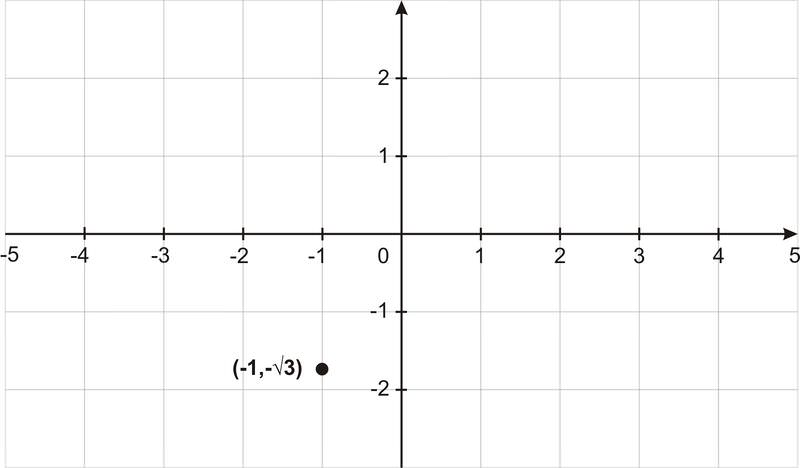
::例1

Graph in polar form: $\begin{aligned} z = - 1 - i \sqrt{3} \end{aligned}$ .
::极形图:z1-i3。

Here is what it looks like in the rectangular coordinate system:
::以下是矩形坐标系统中它的样子:

In polar form, we find r with
::以极地的形式,我们发现R和R

$\begin{aligned} r = \sqrt{a^{2} + b^{2}} \end{aligned}$
::r=a2+b2

$\begin{aligned} = \sqrt{(- 1)^{2} + (- \sqrt{3})^{2}} \end{aligned}$

$\begin{aligned} = \sqrt{1 + 3} \end{aligned}$

$\begin{aligned} = \sqrt{4} \end{aligned}$

$\begin{aligned} = 2 \end{aligned}$

and to find θ ,
::以发现,

$\begin{aligned} tan θ_{r e f} = | \frac{- \sqrt{3}}{- 1} | \end{aligned}$
::-1 -1 -1

$\begin{aligned} tan θ_{r e f} = \sqrt{3} \end{aligned}$
::棕色 & erref= 3

$\begin{aligned} θ_{r e f} = {tan}^{- 1} \sqrt{3} \end{aligned}$
::ref=tan-1 3

$\begin{aligned} θ_{r e f} = \frac{π}{3} \end{aligned}$
::瑞夫3号

Since this angle is in the 4 ^th quadrant, $\begin{aligned} θ = \frac{4 π}{3} \end{aligned}$ .
::由于这个角度位于第四象限 43

Example 2
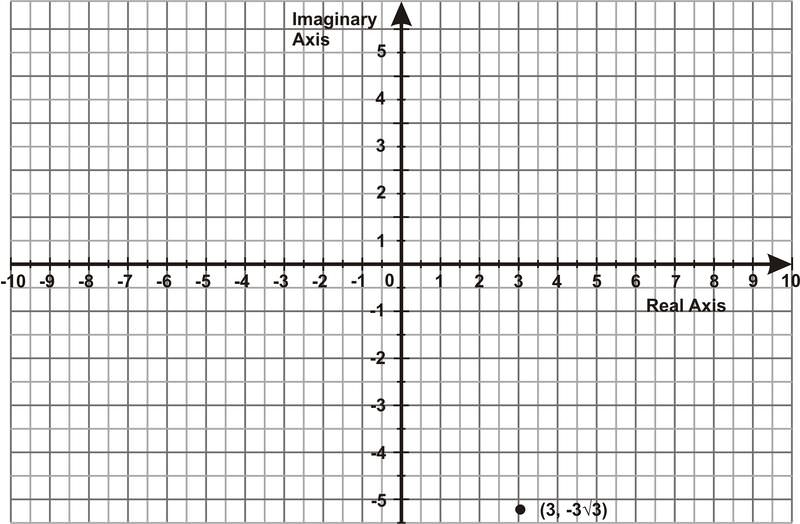
::例2

Find the polar coordinates that represent the complex number $\begin{aligned} z = 3 - 3 \sqrt{3} i \end{aligned}$ .
::查找代表复数z=3-333i的极坐标。

a = 3 and b = $\begin{aligned} - 3 \sqrt{3} \end{aligned}$ : the rectangular coordinates of the point are $\begin{aligned} (3, - 3 \sqrt{3}) \end{aligned}$ .
::a = 3和b =-33:点的矩形坐标为(3,-33)。

Now, draw a right triangle in standard form. Find the distance the point is from the origin and the angle the line segment that represents this distance makes with the +x axis:
::现在, 以标准格式绘制一个右三角形。查找点与 +x 轴代表此距离的线段的起点和角之间的距离 :

We know a = 3, $\begin{aligned} b = - 3 \sqrt{3} \end{aligned}$
::我们知道a=3,b33

$\begin{aligned} r = \sqrt{3^{2} + (- 3 \sqrt{3})^{2}} \end{aligned}$
::r=32+(-33)2

$\begin{aligned} = \sqrt{9 + 27} \end{aligned}$

$\begin{aligned} = \sqrt{36} \end{aligned}$

$\begin{aligned} = 6 \end{aligned}$

And for the angle,
::对于角度,

$\begin{aligned} tan θ_{r e f} = | \frac{(- 3 \sqrt{3})}{3} | \end{aligned}$
:- 333)3

$\begin{aligned} tan θ_{r e f} = \sqrt{3} \end{aligned}$
::棕色 & erref= 3

$\begin{aligned} θ_{r e f} = \frac{π}{3} \end{aligned}$
::瑞夫3号

But, since it is a 4 ^th quadrant angle
::但是,既然是第四象限角度

$\begin{aligned} θ = \frac{5 π}{3} \end{aligned}$

The rectangular point $\begin{aligned} (3, - 3 \sqrt{3} i) \end{aligned}$ is equivalent to the polar point $\begin{aligned} (6, \frac{5 π}{3}) \end{aligned}$ .
::矩形点(3,-33i)相当于极点(6,53)。

In rcisθ form, $\begin{aligned} (3, - 3 \sqrt{3} i) \end{aligned}$ is $\begin{aligned} 6 (cos \frac{5 π}{3} + i sin \frac{5 π}{3}) \end{aligned}$ .
::在cis形式中,(3,-33i)为6(53+i sin 53)。

Example 3
::例3

Convert the following complex numbers into polar form, use a TI-84 equivalent graphing calculator:
::将下列复杂数字转换成极形,使用TI-84等量图形计算计算器:

$\begin{aligned} \sqrt{3} - i \end{aligned}$
::3- i 3- i

$\begin{aligned} 9 \sqrt{3} + 9 i \end{aligned}$
::93+9i

On the TI-84: go to [ANGLE] (or [2nd] function) [APPS] . Scroll down to 5 or “R-Pr(“ and press [Enter] . Next, enter the rectangular coordinates and close the parenthesis. Press [Enter] , the “r” value appears. Scroll down to 6R-Pθ, and the polar angle appears in decimal radian form.
::在 TI-84 上: 转到 [ANGLE] (或 [第 2 函数) [APPS] 。向下滚动到 5 或“ R- Pr () ” 或“ 按 [ Enter] 。下一步, 输入矩形坐标并关闭括号。按 [ Enter] , “ r” 值将出现。向下滚动到 6R- P , 极角以小数弧形式出现。

Note: Also under the [ANGLE] menu, commands 7 and 8 allow transformation from polar form to rectangular form.
::注:在[ANGLE]菜单下,指令7和8允许从极形转换成矩形。

Example 4
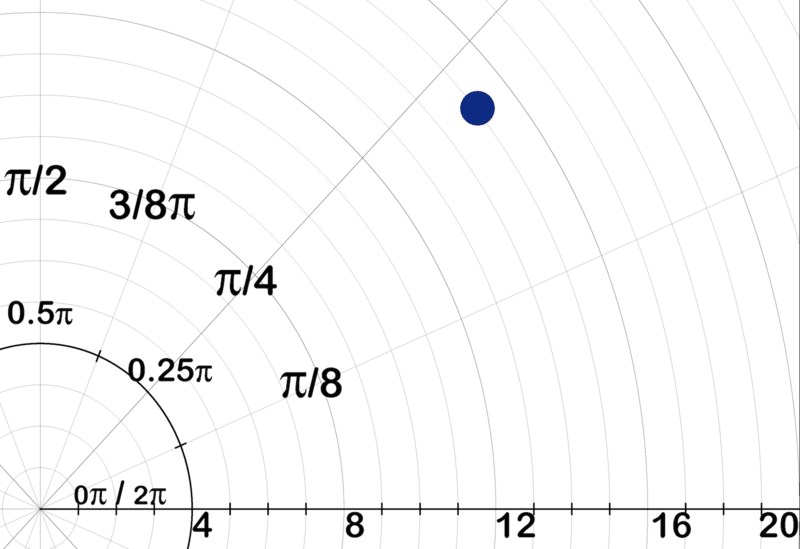
::例4

Plot the complex number $\begin{aligned} z = 12 + 9 i \end{aligned}$ .
::绘制复合号z=12+9i。

What is needed in order to plot this point on the polar plane?
::在极地平面上划出这一点需要什么?

First, we will need to know $\begin{aligned} r \end{aligned}$ and $\begin{aligned} θ \end{aligned}$ .
::首先,我们需要知道。

How could the r-value be determined?
::如何确定r-价值?

The $\begin{aligned} r \end{aligned}$ value is the hypotenuse of a triangle with two other sides, $\begin{aligned} A = 12 \end{aligned}$ and $\begin{aligned} B = 9 \end{aligned}$ . I t can be determined with the Pythagorean theorem: $\begin{aligned} A^{2} + B^{2} = C^{2} \end{aligned}$ .
::热值是三角形与另外两面(A=12和B=9)的光值。可以用Pythagorean定理:A2+B2=C2来测定。

What is the r for this point?
::这一点有什么用?

The $\begin{aligned} r \end{aligned}$ value for this point is $\begin{aligned} \sqrt{144 + 81} \to \sqrt{225} = 15 \end{aligned}$ .
::此点的值为 144+81_225=15。

How could $\begin{aligned} θ \end{aligned}$ be determined?
::如何确定 ?

$\begin{aligned} θ \end{aligned}$ can be calculated using either $\begin{aligned} s i n θ = \frac{9}{15} \end{aligned}$ or $\begin{aligned} c o s θ = \frac{12}{15} \end{aligned}$ .
::可以用任何一种sin\\\\\915orcos\\\\\\\\\1215计算。

What is $\begin{aligned} θ \end{aligned}$ for this point?
::这一点是什么?

For this point, $\begin{aligned} s i n θ = \frac{3}{5} \to 37^{o} \end{aligned}$ or $\begin{aligned} c o s θ = \frac{4}{5} \to 37^{o} \end{aligned}$ .
::对于这一点,sin3537oorcos4537o。

What would $\begin{aligned} z = 12 + 9 i \end{aligned}$ look like on the polar plane?
::在极地平面上Z=12+9i会是什么样子?

$\begin{aligned} z = 12 + 9 i \end{aligned}$ looks like the image below when plotted on a polar plane.
::z=12+9i 绘制在极平面上时看起来像下面的图像。

Example 5
::例5

What quadrant does $\begin{aligned} z = - 3 + 2 i \end{aligned}$ occur in when graphed?
::当图表显示时, z3+2i 会出现什么象限 ?

The point $\begin{aligned} z = - 3 + 2 i \end{aligned}$ occurs 3 units to the left and 2 units up , placing it in Quadrant II.
::3+2occur 左侧3个单位, 左侧2个单位, 放置在 Quadrant II 中。

Example 6
::例6

What are the coordinates of z = -3 + 2i in polar form and trigonometric form?
::Z = -3 + 2i 的极形和三角形坐标是多少?

To identify the coordinates of $\begin{aligned} z = - 3 + 2 i \end{aligned}$ in polar form and trigonometric form:
::确定 z3+2i 的极形和三角形坐标:

$\begin{aligned} r = \sqrt{(- 3^{2}) + (2^{2})} \to \sqrt{13} \end{aligned}$ First find $\begin{aligned} r \end{aligned}$
::r=(-32)+(22)_13

$\begin{aligned} s i n θ = \frac{2}{\sqrt{13}} \to {33.7}^{o} \end{aligned}$ Second, find $\begin{aligned} θ \end{aligned}$
::第二,找到

$\begin{aligned} ∴ [\sqrt{13}, {33.7}^{o}] \end{aligned}$ are the coordinates in polar form.
::[13,33.7o]是极形坐标。

$\begin{aligned} ∴ r c i s \sqrt{13} (\frac{π}{5}) \end{aligned}$ are the coordinates in $\begin{aligned} r c i s \end{aligned}$ form
::rcis13(______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Example 7
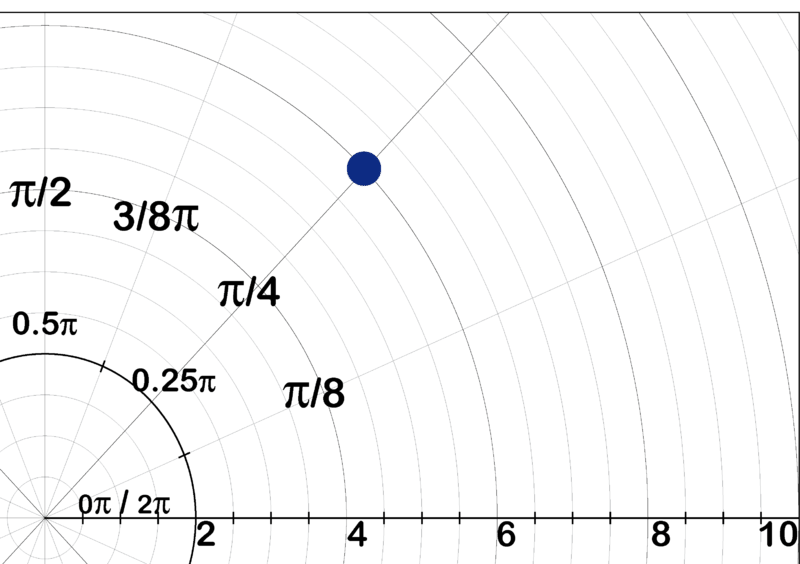
::例7

What would be the polar coordinates of the point graphed below?
::下图显示的点的极地坐标是多少?

The rectangular coordinates are (4.5, 3i) therefore the complex number would be $\begin{aligned} z = 4.5 + 3 i \end{aligned}$
::矩形坐标为(4.5, 3i),因此复合号为z=4.5+3i

$\begin{aligned} r = 5.4 \end{aligned}$ Using the Pythagorean Theorem as in Q #3
::r=5.4 使用Q #3中的毕达哥里定理

$\begin{aligned} θ = {33.75}^{o} \end{aligned}$ Using $\begin{aligned} s i n = \frac{o p p}{h y p} \end{aligned}$ as in Q #3
::33.75o 使用 sin=opopphyp如 Q # 3 中的 sin=opphyp 。

$\begin{aligned} ∴ [5.4, {33.65}^{o}] \end{aligned}$ is the point in polar form $\begin{aligned} ∴ r c i s 5.4 (\frac{π}{5}) \end{aligned}$ are the coordinates in $\begin{aligned} r c i s \end{aligned}$ form
::[5.4,33.65o] 是极形的点 rcis5.4(5) 是以 rcis 格式的坐标。

Review
::回顾

Plot each complex number in the complex plane. Find its polar form, $\begin{aligned} [r, θ] \end{aligned}$ and give the argument $\begin{aligned} θ \end{aligned}$ in degrees.
::在复杂的平面中绘制每个复数。查找其极形 [r, }] 并以度表示参数。

a) $\begin{aligned} 1 + i \end{aligned}$ b) $\begin{aligned} i \end{aligned}$ c) $\begin{aligned} (1 + i) i \end{aligned}$
:a) 1+一(b)一(c)一(1+一)(一)一

a) $\begin{aligned} - 2 \end{aligned}$ b) $\begin{aligned} 3 i \end{aligned}$ c) $\begin{aligned} (- 2) (3 i) \end{aligned}$
:a)-2(b)-3i(c)-2(3i)

a) $\begin{aligned} 1 + i \end{aligned}$ b) $\begin{aligned} 1 - i \end{aligned}$ c) $\begin{aligned} (1 + i) (1 - i) \end{aligned}$
:a) 1+一(b) 1-一(c) 1+一(一) 1-一(一)

a) $\begin{aligned} 1 + i \sqrt{3} \end{aligned}$ b) $\begin{aligned} \sqrt{3} - i \end{aligned}$ c) $\begin{aligned} (1 + i \sqrt{3}) (\sqrt{3} - i) \end{aligned}$
:a) 1+i3(b) 3-i c(1+i3)(3-i)

What are the rectangular coordinates for the point graphed below?
::下图点的矩形坐标是多少?

Compute and convert to $\begin{aligned} r c i s \end{aligned}$ form.
::计算并转换为 rcis 窗体。

$\begin{aligned} \frac{- 2 - 2 i}{1 - i} \end{aligned}$
::--2-2-2-i-1-i

$\begin{aligned} 1 + i^{6} \end{aligned}$
::1+i6 1+i6

$\begin{aligned} \frac{\sqrt{3}}{2} + \frac{1}{2} i^{10} \end{aligned}$
::32+12i10

Change to polar form.
::改变为极形。

$\begin{aligned} - 3 - 2 i \end{aligned}$
::- 3-2i

$\begin{aligned} 2 \sqrt{3} - 2 i \end{aligned}$
::23-2i 23-2ii

Change to rectangular form.
::更改为矩形。

$\begin{aligned} 15 (c o s 120^{o} + i s i n 120^{o}) \end{aligned}$
::15(cos120o+isin120o)

$\begin{aligned} 12 (c o s \frac{π}{3} + i s i n \frac{π}{3}) \end{aligned}$
::12(cos%3+isin%3) 3

For the complex number in standard form $\begin{aligned} x + i y \end{aligned}$ find: a) Polar form b) Trigonometric form (Hint: Recall that $\begin{aligned} x = r c o s θ \end{aligned}$ and $\begin{aligned} y = r s i n θ \end{aligned}$ )
::标准表x+iy 查找的复数 : a) 极表 b) 三角度度表(提示: 提醒注意 x=rcos- 和 y=rsin )

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Polar Form of Complex Numbers ::复数极表

Summary of Forms ::形式摘要

Steps for Conversion ::转换步骤

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)

Polar Form of Complex Numbers
::复数极表

Summary of Forms
::形式摘要

Steps for Conversion
::转换步骤

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Review
::回顾

Review (Answers)
::回顾(答复)