角的终端侧端点点的三角比

播放段落

Trig Riddle: I am the point $\begin{align*}(1, -3)\end{align*}$ . What are my ?
::Trig Riddle:我才是重点(1,3),

播放段落

Trigonometric Ratios of Points
::点的三角比

播放段落

Any point in the coordinate plane can be represented by its angle of rotation and radius, or distance from the origin. The point is said to lie on the terminal side of the angle. We can find the measure of the reference angle using . When the point is identified in this manner we call the coordinates Polar coordinates. They are written as $\begin{align*}(r, \theta)\end{align*}$ , where $\begin{align*}r\end{align*}$ is the radius and $\begin{align*}\theta\end{align*}$ is the angle of rotation. The angle of rotation can be given in degrees or radians.
::坐标平面中的任何点都可以以其旋转角度和半径表示,或以其起点的距离表示。 指点据说位于角度的终点侧。 我们可以找到使用引用角度的量度 。 当点以这种方式被确定为坐标极坐标时, 我们称之为极坐标坐标 。 它们写成(r, r) , r 是半径, 是旋转角度 。 旋转角度可以以度或弧度表示 。

播放段落

Let's find the angle of rotation (in degrees) and radius (distance from the origin) of the point $\begin{align*}(-3, 6)\end{align*}$ .
::让我们找到点的旋转角度( 以度计) 和半径角度( 与原点的距离) (- 3, 6) 。

播放段落

First, make a sketch, plot the point and drop a perpendicular to the $\begin{align*}x\end{align*}$ -axis to make a right triangle.
::首先,做一个草图,绘制点,然后将一个直角投到x轴上,形成一个右三角形。

播放段落

From the sketch, we can see that $\begin{align*}\tan^{-1} \left(-\frac{6}{3} \right)=63.4^\circ\end{align*}$ is the reference angle so the angle of rotation is $\begin{align*}180^\circ-63.4^\circ=116.6^\circ\end{align*}$ .
::从草图中可以看出,Tan-1(-63)=63.4是参考角度,旋转角度为18063.4116.6。

播放段落

The radius or distance from the origin is the hypotenuse of the right triangle.
::半径或距离来源是右三角形的下限。

播放段落

$$\begin{align*}r^2 &=(-3)^2+(6)^2 \\ r^2 &=45 \\ r &=\sqrt{45}=3\sqrt{5}\end{align*}$$
::r2=(-3)2+(6)2r2=45r=45=35

播放段落

Using this information, we can write the point $\begin{align*}(-3, 6)\end{align*}$ in Polar coordinate form as $\begin{align*}\left ( 3 \sqrt{5}, 116.6^\circ \right )\end{align*}$
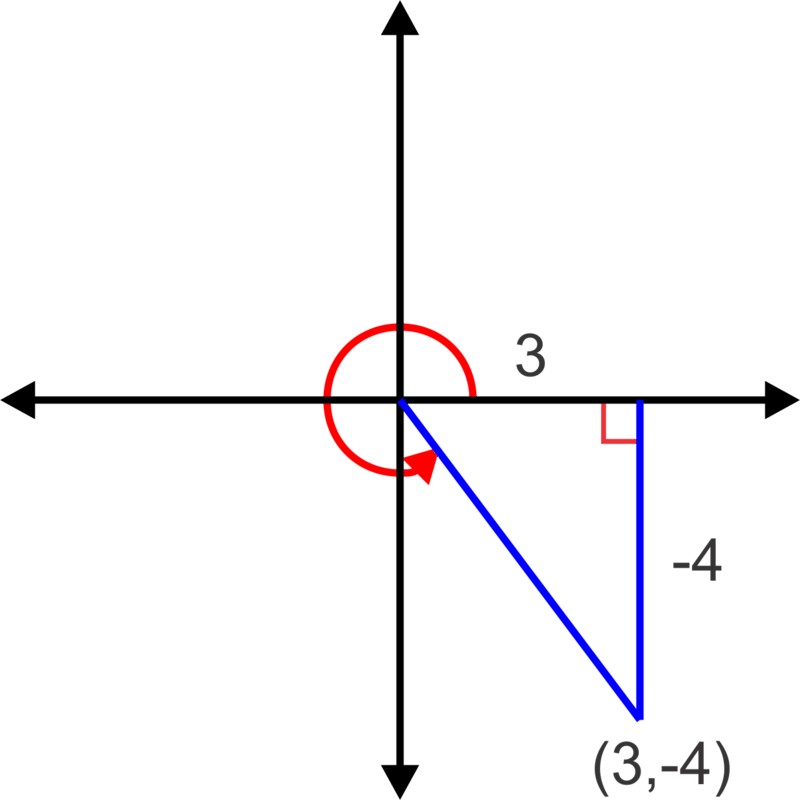
::使用这一信息,我们可以用极地坐标表填写点(-3,6)为(35,116.6)。

播放段落

Now, let's write the Cartesian coordinates, $\begin{align*}(3, -4)\end{align*}$ , in Polar form and give the angle in degrees.
::现在,让我们以极地形式写下笛卡尔座标(3, - 4), 并以度表示角度。

播放段落

Again, start with a sketch.
::再来,从草图开始

播放段落

We can find the reference angle again using tangent: $\begin{align*}\tan^{-1} \left(\frac{-4}{3} \right)=-53.1^\circ\end{align*}$ . So the angle of rotation is $\begin{align*}360^\circ-53.1^\circ=306.9^\circ\end{align*}$
::使用正切度: tan-1(- 43) 53.1\\\\\\\\\\\\\\可以再次找到参考角度。 因此旋转的角度是 360\\\53.1\\\\306. 9\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

播放段落

Now find the radius:
::现在找到半径 :

播放段落

$$\begin{align*}r^2 &=3^2+(-4)^2 \\ r^2 &=25 \\ r &=\sqrt{25}=5\end{align*}$$
::r2=32+(-4)2r2=25r=5

播放段落

The Polar coordinates are thus $\begin{align*}(5, 306.9^\circ)\end{align*}$
::因此,极地坐标为(5,306.9)

播放段落

Note: You may have noticed that there is a pattern that gives us a short cut for finding the Polar coordinates for any Cartesian coordinates, $\begin{align*}(x, y)\end{align*}$ :
::注意:你可能已经注意到 有一种模式 给我们一个捷径 来找到 任何笛卡尔座标的极地坐标, (x,y) :

播放段落

The reference angle can be found using, $\begin{align*}\theta=\tan^{-1} \left(\frac{y}{x} \right)\end{align*}$ and then the angle of rotation can be found by placing the reference angle in the appropriate quadrant and giving a positive angle of rotation from the positive $\begin{align*}x\end{align*}$ – axis $\begin{align*}(0^\circ \le \theta < 360^\circ\end{align*}$ or $\begin{align*}0 \le \theta < 2 \pi)\end{align*}$ . The radius is always $\begin{align*}r=\sqrt{x^2+y^2}\end{align*}$ and should be given in reduced radical form.
::参考角可以使用 tan-1(yx) 找到,然后通过将参考角放在适当的象限中找到旋转角度,并从正x - 轴( 0360 或 02) 中给出一个积极的旋转角度。 半径总是 rx2+y2 , 并且应该以降低的激进形式给出。

播放段落

Finally, given the point $\begin{align*}(-9, -5)\end{align*}$ on the terminal side of an angle, let's find the Polar coordinates (in radians) of the point and the six trigonometric ratios for the angle.
::最后,鉴于角度终点的点(- 9) 5, 让我们找到点的极地坐标( 以弧度计) 和角的六个三角比 。

播放段落

Make sure your calculator is in radian mode. Using the shortcut, we can find the Polar coordinates:
::确保您的计算器为弧度模式。 使用快捷键, 我们可以找到极坐标 :

播放段落

$\begin{align*}\tan^{-1} \left(\frac{5}{9} \right)=0.51\end{align*}$ . Since $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ are both negative, the point lies in the third quadrant which makes the angle of rotation $\begin{align*}\pi+0.51=3.65\end{align*}$ . The radius will be $\begin{align*}r=\sqrt{9^2+5^2}=\sqrt{106}\end{align*}$ . The Polar coordinates are $\begin{align*}\left(\sqrt{106}, 3.65\right)\end{align*}$ . As for the six trigonometric ratios, a diagram will help us:
::由于 x 和 y 均为负值, 点位于第三象方块, 该方块使旋转角度 = 0..51= 3.65。 半径为 r92+52=106。 极地坐标是 (106, 3.65) 。 至于六位三角比, 图表将帮助我们:

播放段落

We already know that $\begin{align*}\tan 3.65=\frac{5}{9}\end{align*}$ , so $\begin{align*}\cot 3.65=\frac{9}{5}\end{align*}$ .
::我们已经知道Tan3.65=59, 所以cott3.65=95。

播放段落

Now we can use the hypotenuse, $\begin{align*}\sqrt{106}\end{align*}$ to find the other ratios:
::现在,我们可以用下限106来找到其他比率:

播放段落

$\begin{align*}\sin 3.65 =\frac{-5}{\sqrt{106}}=-\frac{5 \sqrt{106}}{106}\end{align*}$ and $\begin{align*}\csc 3.65=-\frac{\sqrt{106}}{5}\end{align*}$ .
::和csc3.651065。

播放段落

$\begin{align*}\cos 3.65 =\frac{-9}{\sqrt{106}}=-\frac{9 \sqrt{106}}{106}\end{align*}$ and $\begin{align*}\sec 3.65=-\frac{\sqrt{106}}{9}\end{align*}$
::秒3.6591069106和秒3.651069

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked to find  the polar coordinates of the point  $\begin{align*}(1, -3)\end{align*}$ .
::早些时候,有人要求你找到点(1, - 3)的极地坐标。

播放段落

First, make a sketch, plot the point and drop a perpendicular to the $\begin{align*}x\end{align*}$ -axis to make a right triangle.
::首先,做一个草图,绘制点,然后将一个直角投到x轴上,形成一个右三角形。

播放段落

From the sketch, we can see that $\begin{align*}\tan^{-1} \left(-\frac{3}{1} \right)=-71.6^\circ\end{align*}$ is the reference angle. The point $\begin{align*}(1, -3)\end{align*}$ is in the fourth quadrant, so the angle of rotation is $\begin{align*}360^\circ+\left(-71.6^\circ\right)=288.43^\circ\end{align*}$ .
::从草图中可以看出,Tan-1(--31)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

播放段落

The radius or distance from the origin is the hypotenuse of the right triangle.
::半径或距离来源是右三角形的下限。

播放段落

$$\begin{align*}r^2 &=(1)^2+(-3)^2 \\ r^2 &=10 \\ r &=\sqrt{10}\end{align*}$$
::r2=(1)2+(-3)2r2=10r10

播放段落

Therefore, my polar coordinates are $\begin{align*}\left ( \sqrt{10}, 288.4^\circ \right )\end{align*}$ .
::因此,我的极地坐标是(10,288.4)。

播放段落

Example 2
::例2

播放段落

Find the angle of rotation (in degrees) and radius (distance from the origin) of the point $\begin{align*}(7, 24)\end{align*}$ .
::查找点(7,24)的旋转角度(以度计)和半径(从原点的距离) 。

播放段落

$\begin{align*}r=\sqrt{7^2+24^2}=25\end{align*}$ , $\begin{align*}\theta=\tan^{-1} \left(\frac{24}{7} \right) \approx 73.7^\circ\end{align*}$
::72+242=25,tan-1(247)73.7

播放段落

Example 3
::例3

播放段落

Write the Cartesian coordinates, $\begin{align*}(-8, -15)\end{align*}$ , in Polar form(in radians) and find the six trigonometric ratios for the angle.
::以极地形式(以弧度)写出笛卡尔座标(-8-15),并找到角的六个三角比。

播放段落

$\begin{align*}r=\sqrt{(-8)^2+(-15)^2}=17\end{align*}$ and $\begin{align*}\theta=\tan^{-1} \left(\frac{-15}{-8} \right) \approx 1.08\end{align*}$ so the polar coordinates are $\begin{align*}(17, 1.08)\end{align*}$ .
::r(-8)2+(-15)2=17和tan-1(-15-8)1.08,所以极地坐标是(171.08)。

播放段落

The six trigonometric ratios are:

$$\begin{align*}\sin 1.08 &=-\frac{15}{17} \quad \csc 1.08 =-\frac{17}{15} \\ \cos 1.08 &=-\frac{8}{17} \quad \sec 1.08 =-\frac{8}{15} \\ \tan 1.08 &=\frac{15}{8} \quad \ \ \cot 1.08 =-\frac{8}{15}\end{align*}$$
::6个三角比率是: sin1.081517csc1.081715cos1.08817sec1.08815tan1.08=158 ct1.08815

播放段落

Example 4
::例4

播放段落

Given the point $\begin{align*}(12, -4)\end{align*}$ on the terminal side of an angle, find the Polar coordinates (in degrees) of the point and the six trigonometric ratios for the angle.
::参照角度末端的点(12,-4),找到点的极地坐标(度)和角的六个三角比。

播放段落

$\begin{align*}r=\sqrt{12^2+(-4)^2}=4 \sqrt{10}\end{align*}$ and $\begin{align*}\theta=\tan^{-1} \left(\frac{-4}{12} \right) \approx 341.6^\circ\end{align*}$ so the polar coordinates are $\begin{align*}\left(4 \sqrt{10}, 341.6^\circ\right)\end{align*}$ .
::r122+(-4)2=410和tan-1(-412)341.6,所以极坐标是(410,341.6)。

播放段落

The six trigonometric ratios are:

$$\begin{align*}\sin 341.6^\circ &=-\frac{\sqrt{10}}{10} \quad \csc 341.6^\circ=-\sqrt{10} \\ \cos 341.6^\circ &=\frac{3 \sqrt{10}}{10} \quad \csc 341.6^\circ=\frac{\sqrt{10}}{3} \\ \tan 341.6^\circ &=-\frac{1}{3} \quad \ \ \ \tan 341.6^\circ=-3\end{align*}$$
::6个三角比率是:sin341.61010csc341.610cos341.610cos341.631010cscc341.6103tan341.613tan341.63

播放段落

Review
::回顾

播放段落

Angle measures should be rounded to the dearest degree or hundredth of a radian or given exactly if possible. All values of $\begin{align*}r\end{align*}$ should be given in reduced radical form.
::角度量应四舍五入至最宝贵的弧度或弧度的一百分之一或一百分之一,或者尽可能精确地给出。 r的所有值均应以降低的激进形式给出。

播放段落

Write the following Cartesian coordinate pairs in Polar form. Use degrees for problems 1 and 2 and radians for problems 3-5.
::以极地形式写下下列笛卡尔坐标对。问题1和2使用度,问题3至5使用弧度。

1. $\begin{align*}(16, -30)\end{align*}$
2. $\begin{align*}(5, 5)\end{align*}$
3. $\begin{align*}(-5, -12)\end{align*}$
4. $\begin{align*}(-9, 40)\end{align*}$
5. $\begin{align*}(-4, 8)\end{align*}$

播放段落

Given the points on the terminal side of an angle, find the Polar coordinates (in degrees) of the point and the six trigonometric ratios for the angles.
::根据角端端的点数,找到点的极地坐标(度)和角的六个三角比。

6. $\begin{align*}(-6, 8)\end{align*}$
7. $\begin{align*}(0, -15)\end{align*}$
8. $\begin{align*}(10, -8)\end{align*}$
9. $\begin{align*}\left(4 \sqrt{3}, 4\right)\end{align*}$
10. $\begin{align*}(-6, 6)\end{align*}$

播放段落

Given the points on the terminal side of an angle, find the Polar coordinates (in radians) of the point and the six trigonometric ratios for the angles.
::根据角端端的点数,找到点的极地坐标(以弧度计)和角的六个三角比。

11. $\begin{align*}(-9, 0)\end{align*}$
12. $\begin{align*}(13, -13)\end{align*}$
13. $\begin{align*}(2, 3)\end{align*}$
14. $\begin{align*}\left(-7, -7 \sqrt{3}\right)\end{align*}$
15. $\begin{align*}(-8, -4)\end{align*}$

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。