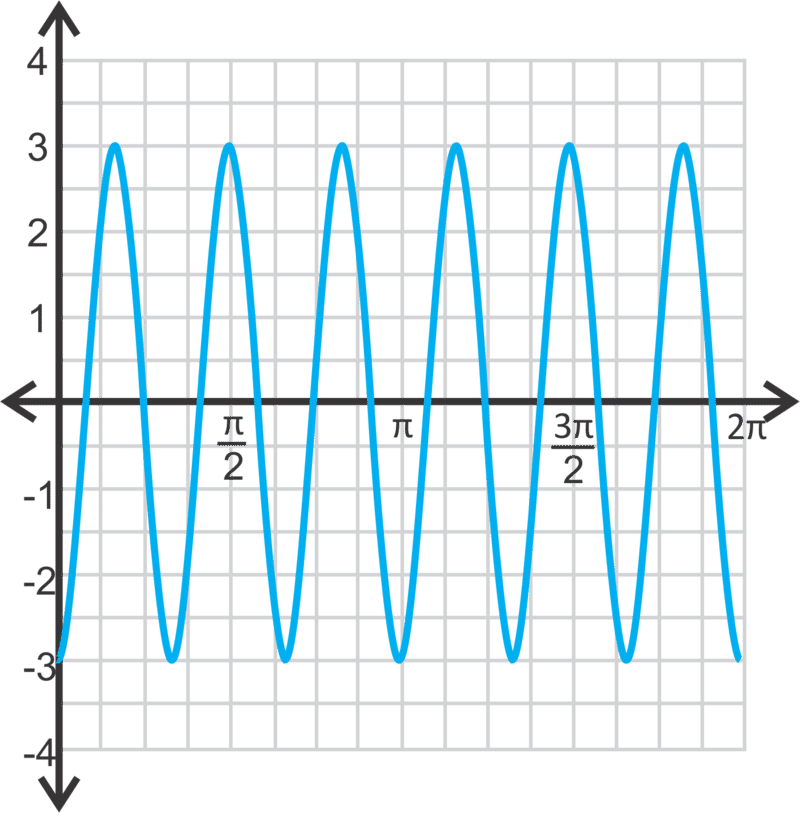
节: Sine 和 Cosine 函数期间的变化 | 14.4 Sine 和 Cosine 函数期间的变化

章节大纲

Your mission, should you choose to accept it, as Agent Trigonometry is to find the period of the cosine function $\begin{aligned} y = \cos [π (2 x + 4)] \end{aligned}$ .
::您的任务, 如果您选择接受它, 因为代理 Trigonology 是要找到连接函数 y= cos[%( 2x+4)] 的时间段。

Period
::期间

The last thing that we can manipulate on the curve is the period .
::在曲线上我们能操纵的最后一件事就是时间

The normal period of a sine or cosine curve is $\begin{aligned} 2 π \end{aligned}$ . To stretch out the curve, then the period would have to be longer than $\begin{aligned} 2 π \end{aligned}$ . Below we have sine curves with a period of $\begin{aligned} 4 π \end{aligned}$ and then the second has a period of $\begin{aligned} π \end{aligned}$ .
::正弦或余弦曲线的正常时间段为 2。要拉开曲线, 时间段必须大于 2 。在下方, 中间曲线为 4 , 而第二个曲线为 __ 。

To determine the period from an equation, we introduce $\begin{aligned} b \end{aligned}$ into the general equation. So, the equations are $\begin{aligned} y = a \sin b (x - h) + k \end{aligned}$ and $\begin{aligned} y = a \cos b (x - h) + k \end{aligned}$ , where $\begin{aligned} a \end{aligned}$ is the , $\begin{aligned} b \end{aligned}$ is the frequency , $\begin{aligned} h \end{aligned}$ is the phase shift , and $\begin{aligned} k \end{aligned}$ is the vertical shift . The frequency is the number of times the sine or cosine curve repeats within $\begin{aligned} 2 π \end{aligned}$ . Therefore, the frequency and the period are indirectly related. For the first sine curve, there is half of a sine curve in $\begin{aligned} 2 π \end{aligned}$ . Therefore the equation would be $\begin{aligned} y = \sin \frac{1}{2} x \end{aligned}$ . The second sine curve has two curves within $\begin{aligned} 2 π \end{aligned}$ , making the equation $\begin{aligned} y = \sin 2 x \end{aligned}$ . To find the period of any sine or cosine function, use $\begin{aligned} \frac{2 π}{| b |} \end{aligned}$ , where $\begin{aligned} b \end{aligned}$ is the frequency. Using the first graph above, this is a valid formula: $\begin{aligned} \frac{2 π}{\frac{1}{2}} = 2 π \cdot 2 = 4 π \end{aligned}$ .
::为了确定方程的周期, 我们将 b 引入一般方程。因此, 方程是 y=asinb( x- h)+k 和 y=acosb( x- h)+k, 其中, a 是 , b 是频率, h 是相位变化, k 是垂直变化。频率是正弦或正弦曲线在 2 ° 内的重复次数。因此, 频率和周期是间接相关的。对于第一个正弦曲线, 在 2 ° 中有一个正弦曲线的一半。因此, 等式是 y= sin\ 12x 。第二个正弦曲线在 2 ° 内有两个曲线, 使 y = six 。要找到正弦或正弦函数的期间, 请使用 2 b , 其中 b 是的频率。因此, 使用上面的第一个图形, 这是有效的公式 : 2: 12= 22 = = 4\ 。

Let's determine the period of the following sine and cosine functions.
::我们来决定下个正弦和连弦函数的周期。

$\begin{aligned} y = - 3 \cos 6 x \end{aligned}$
::y3cos=6x y3cos=6x y3cos=6x

The 6 in the equation tells us that there are 6 repetitions within $\begin{aligned} 2 π \end{aligned}$ . So, the period is $\begin{aligned} \frac{2 π}{6} = \frac{π}{3} \end{aligned}$ .
::等式中的6告诉我们,2内重复了6次。所以,这一时期是263。

$\begin{aligned} y = 2 \sin \frac{1}{4} x \end{aligned}$
::y=2sin=14x

The $\begin{aligned} \frac{1}{4} \end{aligned}$ in the equation tells us the frequency. The period is $\begin{aligned} \frac{2 π}{\frac{1}{4}} = 2 π \cdot 4 = 8 π \end{aligned}$ .
::方程式中的 14 表示频率。周期是 2 14 = 2 4 = 8 。

$\begin{aligned} y = \sin π x - 7 \end{aligned}$
::y=sin_x-7 y=sin_x-7

The $\begin{aligned} π \end{aligned}$ is the frequency. The period is $\begin{aligned} \frac{2 π}{π} = 2 \end{aligned}$ .
::频率为 __ 。周期为 2 __ 2 。

Now, let's graph $\begin{aligned} y = - 3 \cos 6 x \end{aligned}$ from $\begin{aligned} [0, 2 π] \end{aligned}$ , determine where the maximum and minimum values occur, and state the domain and range.
::现在,让我们从 [ 0, 2] 绘制 y3cos6x, 确定最大值和最小值的发生地点, 并指定域和范围。

The amplitude is -3, so it will be stretched and flipped. The period is $\begin{aligned} \frac{π}{3} \end{aligned}$ (from above) and the curve should repeat itself 6 times from 0 to $\begin{aligned} 2 π \end{aligned}$ . The first maximum value is 3 and occurs at half the period, or $\begin{aligned} x = \frac{π}{6} \end{aligned}$ and then repeats at $\begin{aligned} x = \frac{π}{2}, \frac{5 π}{6}, \frac{7 π}{6}, \frac{3 π}{2}, \dots \end{aligned}$ Writing this as a formula we start at $\begin{aligned} \frac{π}{6} \end{aligned}$ and add $\begin{aligned} \frac{π}{3} \end{aligned}$ to get the next maximum, so each point would be $\begin{aligned} (\frac{π}{6} \pm \frac{π}{3} n, 3) \end{aligned}$ where $\begin{aligned} n \end{aligned}$ is any integer.
::振幅为 - 3, 将会被拉伸和翻转。时段为 +3 (以上) , 曲线应该从 0 到 2 重复 6 倍。第一个最大值为 3 , 半个 , 或 x + 6 , 然后在 x 2, 5 5 6 7 6 6 3+2 重复... 将此写成一个公式, 我们从 _ 6 开始, 并添加 3 3 以获得下一个最大值, 所以每个点都是 n 是整数的 6 6 3 。

The minimums occur at -3 and the $\begin{aligned} x \end{aligned}$ -values are multiples of $\begin{aligned} \frac{π}{3} \end{aligned}$ . The points would be $\begin{aligned} (\pm \frac{π}{3} n, - 3) \end{aligned}$ , again $\begin{aligned} n \end{aligned}$ is any integer. The domain is all real numbers and the range is $\begin{aligned} y \in [- 3, 3] \end{aligned}$ .
::最小值在 - 3 时为 - 3, x 值是 3 的倍数。点数是 (3n, -3) , n 也是任何整数。域是所有实际数字, 范围是 y { 3, 3) 。

Finally, let's find all the solutions from the function $\begin{aligned} y = 2 \sin \frac{1}{4} x \end{aligned}$ from $\begin{aligned} [0, 2 π] \end{aligned}$ .
::最后,让我们从 y=2sin14x 函数 [0,2] 中找到所有解决方案。

Now that the period can be different, we can have a different number of zeros within $\begin{aligned} [0, 2 π] \end{aligned}$ . In this case, we will have 6 times the number of zeros that the parent function. To solve this function, set $\begin{aligned} y = 0 \end{aligned}$ and solve for $\begin{aligned} x \end{aligned}$ .
::现在时间可以不同, 我们可以在 [ 0, 2] 内有不同的零数。在这种情况下, 我们的零数将是父函数的零数的六倍。要解析此函数, 请设置 y=0 和 x 的解析。

$\begin{aligned} 0 & = - 3 \cos 6 x \\ 0 & = \cos 6 x \end{aligned}$

::03cos=6x0=cos=6xx

Now, use the inverse cosine function to determine when the cosine is zero. This occurs at the multiples of $\begin{aligned} \frac{π}{2} \end{aligned}$ .
::现在,使用反余弦函数来确定余弦为零的时间。这发生在% 2 的倍数上。

$\begin{aligned} 6 x = \cos^{- 1} 0 = \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, \frac{7 π}{2}, \frac{9 π}{2}, \frac{11 π}{2}, \frac{13 π}{2}, \frac{15 π}{2}, \frac{17 π}{2}, \frac{19 π}{2}, \frac{21 π}{2}, \frac{23 π}{2} \end{aligned}$

::6x=cos-102,32,52,52,72,72,92,112,112,132,152,172,172,192,212,232

We went much past $\begin{aligned} 2 π \end{aligned}$ because when we divide by 6, to get $\begin{aligned} x \end{aligned}$ by itself, all of these answers are going to also be divided by 6 and smaller.
::我们过去很多年了,因为当我们除以6来获得x本身时,所有这些答案也将除以6和较小。

$\begin{aligned} x = \frac{π}{12}, \frac{π}{4}, \frac{5 π}{12}, \frac{7 π}{12}, \frac{3 π}{4}, \frac{11 π}{12}, \frac{13 π}{12}, \frac{5 π}{4}, \frac{17 π}{12}, \frac{19 π}{12}, \frac{21 π}{2}, \frac{23 π}{12} \end{aligned}$

::12, 4, 5, 5, 12, 3, 4, 11, 12, 13, 12, 5, 4, 17, 12, 19, 12, 212, 23, 12

$\begin{aligned} \frac{23 π}{12} < 2 π \end{aligned}$ so we have found all the zeros in the range.
::2312<2 ┮и祇瞷┮Τ零

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the period of $\begin{aligned} y = \cos [π (2 x + 4)] \end{aligned}$ .
::早些时候,有人要求你找到y=cos[(2x+4)]的时期。

First, we need to get the function in the form $\begin{aligned} y = a \cos b (x - h) + k \end{aligned}$ . Therefore we need to factor out the 2.
::首先,我们需要以 y=acosb(x-h)+k 的形式获得函数。因此,我们需要将 2 考虑在内。

$\begin{aligned} y = \cos [π (2 x + 4)] \\ y = \cos [2 π (x + 2)] \end{aligned}$

::y=cos[( 2x+4)]y=cos[2x( x+2)]

The $\begin{aligned} 2 π \end{aligned}$ is the frequency. The period is therefore $\begin{aligned} \frac{2 π}{2 π} = 1 \end{aligned}$ .
::频率是 2。因此时间段是 221 。

Example 2
::例2

Determine the period of the function $\begin{aligned} y = \frac{2}{3} \cos \frac{3}{4} x \end{aligned}$ .
::确定函数 y= 23cos = = 34x 的周期。

The period is $\begin{aligned} \frac{2 π}{\frac{3}{4}} = 2 π \cdot \frac{4}{3} = \frac{8 π}{3} \end{aligned}$ .
::报告期为2-34=2_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Example 3
::例3

Find the zeros of the function from Example 2 from $\begin{aligned} [0, 2 π] \end{aligned}$ .
::从例2中 [0,2] 查找函数的零。

The zeros would be when $\begin{aligned} y \end{aligned}$ is zero.
::零是y为0时的零。

$\begin{aligned} 0 & = \frac{2}{3} \cos \frac{3}{4} x \\ 0 & = \cos \frac{3}{4} x \\ \frac{3}{4} x & = \cos^{- 1} 0 = \frac{π}{2}, \frac{3 π}{2} \\ x & = \frac{4}{3} (\frac{π}{2}, \frac{3 π}{2}) \\ x & = \frac{2 π}{3}, 2 π \end{aligned}$

::0=23cos34x0=cos34x34x=cos-102,32x43(2,32)x=23,23

Example 4
::例4

Determine the equation of the sine function with an amplitude of -3 and a period of $\begin{aligned} 8 π \end{aligned}$ .
::确定正弦函数的方程式,其振幅为 -3,期间为 8 。

The general equation of a sine curve is $\begin{aligned} y = a \sin b x \end{aligned}$ . We know that $\begin{aligned} a = - 3 \end{aligned}$ and that the period is $\begin{aligned} 8 π \end{aligned}$ . Let’s use this to find the frequency, or $\begin{aligned} b \end{aligned}$ .
::正弦曲线的一般方程式是 y=asinbx。我们知道 a3 和时间段是 8。让我们用这个来查找频率, 或者 b 。

$\begin{aligned} \frac{2 π}{b} & = 8 π \\ \frac{2 π}{8 π} & = b \\ \frac{1}{4} & = b \end{aligned}$

::2b=828b14=b

The equation of the curve is $\begin{aligned} y = - 3 \sin \frac{1}{4} x \end{aligned}$ .
::曲线的方程是 y3sin14x。

Review
::回顾

Find the period of the following sine and cosine functions.
::查找下列正弦和余弦函数的期间。

$\begin{aligned} y = 5 \sin 3 x \end{aligned}$
::y=5sin=3x y=5sin=3x

$\begin{aligned} y = - 2 \cos 4 x \end{aligned}$
::y2cos=4x y2cos=4x y2cos=4x

$\begin{aligned} y = - 3 \sin 2 x \end{aligned}$
::y=======================================================================================================================================

$\begin{aligned} y = \cos \frac{3}{4} x \end{aligned}$
::y=cos=34x y=cos=34x

$\begin{aligned} y = \frac{1}{2} \cos 2.5 x \end{aligned}$
::y=12cos=2.5x y=12cos=2.5x

$\begin{aligned} y = 4 \sin 3 x \end{aligned}$
::y=4sin=3x y=4sin=3x

Use the equation $\begin{aligned} y = 5 \sin 3 x \end{aligned}$ to answer the following questions.
::使用 y=5sin3x 等式回答下列问题。

Graph the function from $\begin{aligned} [0, 2 π] \end{aligned}$ and find the domain and range.
::从 [0,2] 绘制函数图,并找到域和范围。

Determine the coordinates of the maximum and minimum values.
::确定最大值和最低值的坐标。

Find all the zeros from $\begin{aligned} [0, 2 π] \end{aligned}$ .
::查找 [0,2] 的所有零。

Use the equation $\begin{aligned} y = \cos \frac{3}{4} x \end{aligned}$ to answer the following questions.
::使用 y=cos%34x 等式回答下列问题。

Graph the function from $\begin{aligned} [0, 4 π] \end{aligned}$ and find the domain and range.
::从 [0,4] 绘制函数图,并找到域和范围。

Determine the coordinates of the maximum and minimum values.
::确定最大值和最低值的坐标。

Find all the zeros from $\begin{aligned} [0, 2 π] \end{aligned}$ .
::查找 [0,2] 的所有零。

Use the equation $\begin{aligned} y = - 3 \sin 2 x \end{aligned}$ to answer the following questions.
::使用 y3sin2x 等式回答下列问题。

Graph the function from $\begin{aligned} [0, 2 π] \end{aligned}$ and find the domain and range.
::从 [0,2] 绘制函数图,并找到域和范围。

Determine the coordinates of the maximum and minimum values.
::确定最大值和最低值的坐标。

Find all the zeros from $\begin{aligned} [0, 2 π] \end{aligned}$ .
::查找 [0,2] 的所有零。

What is the domain of every sine and cosine function? Can you make a general rule for the range? If so, state it.
::每个正弦和余弦函数的域是什么? 您能否为范围制定一条通则? 如果是, 请声明。

Write the equation of the sine function, in the form $\begin{aligned} y = a \sin b x \end{aligned}$ , with the given amplitude and period.
::写入正弦函数的方程式, 以 y=asinbx 形式写入, 并写入给定的振幅和时段。

Amplitude: -2 Period: $\begin{aligned} \frac{3 π}{4} \end{aligned}$
::振幅: -2 周期: 3×4

Amplitude: $\begin{aligned} \frac{3}{5} \end{aligned}$ Period: $\begin{aligned} 5 π \end{aligned}$
::振幅:35

Amplitude: 9 Period: 6
::振幅: 9 周期: 6

Challenge Find all the zeros from $\begin{aligned} [0, 2 π] \end{aligned}$ of $\begin{aligned} y = \frac{1}{2} \sin 3 (x - \frac{π}{3}) \end{aligned}$ .
::挑战从 y = 12sin 3 (x) 3 [0,2] 中查找全部零。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Period ::期间

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Period
::期间

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)