Parabolas和分析性分析几何

播放段落

Brandyn is graphing as a part of his homework assignment. He is familiar with the standard form of a parabola : $\begin{align*}y = ax^2\end{align*}$ , and the longer form: $\begin{align*}y - k = a(x - h)^2\end{align*}$ .
::Brandyn在做家庭作业时正在绘制图表。他熟悉抛物线的标准形式:y=ax2, 较长的形式:y-k=a(x-h) 2。

播放段落

On his third problem, he runs into a snag. He has simplified the equation significantly, and has been trying to get it to fit the standard form, but he keeps coming up with this: $\begin{align*}x - 4 = 3(y - 3)^2\end{align*}$ . He can't understand why the y term is the squared one, instead of the x term.
::在第三个问题上,他遇到了一个难题。他大大简化了方程式,并试图使它符合标准格式,但他一直想出:x-4=3(y-3)2。他不明白为什么y这个词是正方的,而不是x的。

播放段落

What is going on here?
::这是怎么回事?

播放段落

Parabolas and Analytic Geometry
::Parabolas和分析性分析几何

播放段落

This is our second lesson on parabolas. In the initial lesson, we explored the parabola using the distance formula, and touched on the use of the focus and directrix. In this lesson, we first examine parabolas from the "analytic geometry" point of view, and then work a few examples with the focus and directrix of a parabola.
::这是我们关于抛物线的第二个教训。 在最初的教训中,我们用距离公式探索了抛物线,并触及了焦点和指针的使用。 在这个教训中,我们首先从“分析几何”的角度来研究抛物线,然后用抛物线的焦点和直线来做几个例子。

播放段落

Finding the Equation of a Parabola Using Analytic Geometry
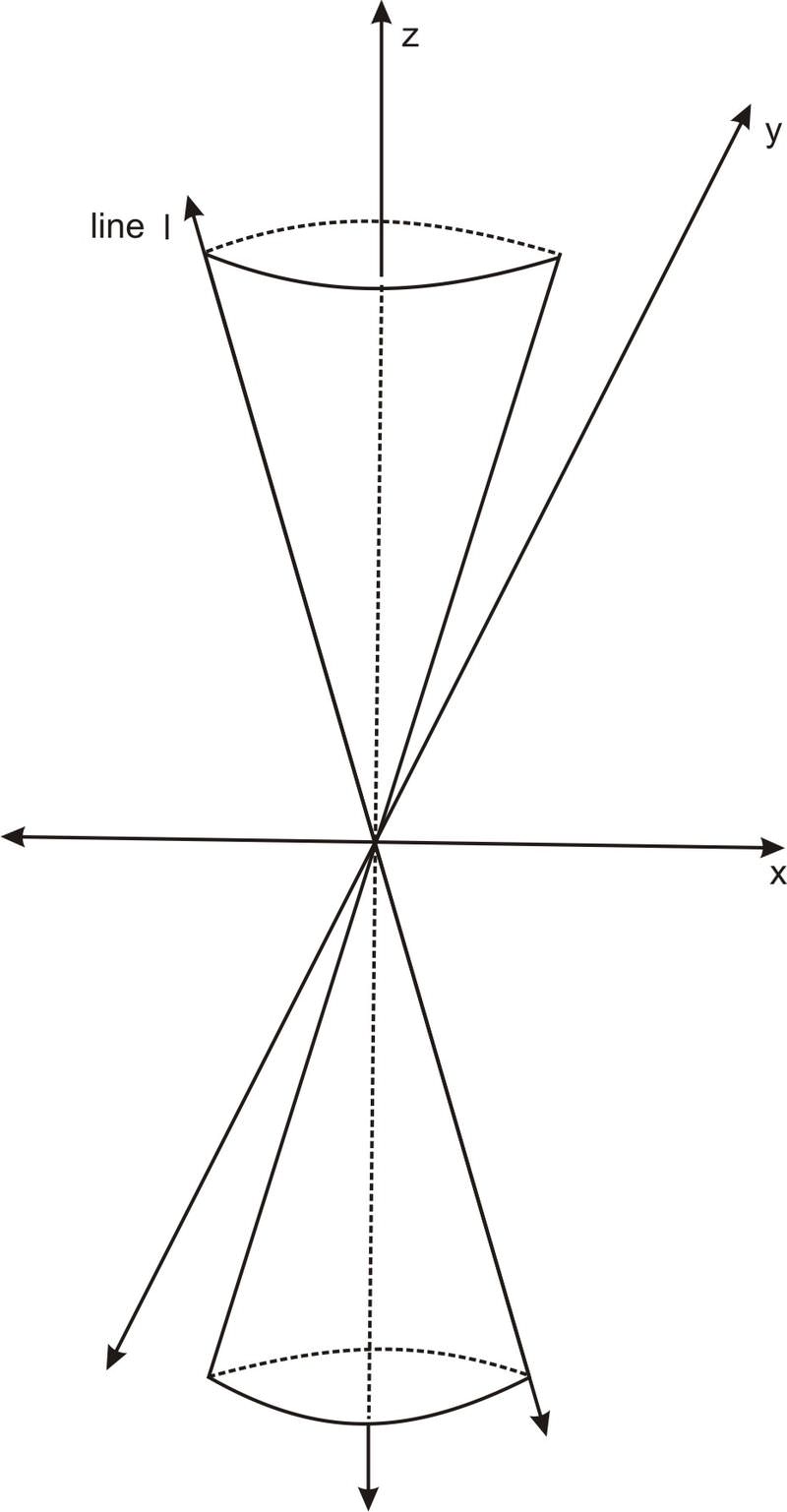
::查找使用分析几何测量法的帕拉波拉的等量

播放段落

Consider a cone oriented in space as pictured below:
::考虑以空间为方向的锥体如下图所示:

播放段落

If the cone opens at an angle such that at any point its radius to height ratio is $\begin{align*}a\end{align*}$ , then the cone could be defined as the set of points such that the distance from the $\begin{align*}z-\end{align*}$ axis is $\begin{align*}a\end{align*}$ times the $\begin{align*}z-\end{align*}$ coordinate. Or, in other words, the set of points $\begin{align*}(x,y,z)\end{align*}$ satisfying:
::如果锥体打开角,其半径与高度之比在任何一点都是一个角,则锥体可被定义为一组点数,以便与z-轴的距离乘以z-坐标。或换句话说,符合以下条件的一组点数(x,y,z):

播放段落

$$\begin{align*}\sqrt{(x - 0)^2 + (y - 0)^2} = az\end{align*}$$
:x-0)2+(y-0)2=az

播放段落

Or:
::或者:

播放段落

$$\begin{align*}x^2 + y^2 = a^2 z^2\end{align*}$$
::x2+y2=a2z2 键

播放段落

This equation works for negative values of $\begin{align*}x, y\end{align*}$ , and $\begin{align*}z\end{align*}$ , giving the general equation for a two-sided cone.
::这个方程式对 X、y 和 z 的负值起作用, 给出了双面方块的总方程式 。

播放段落

To consider the intersection of this cone with a plane that is parallel to the line marked $\begin{align*}l\end{align*}$ marked in the diagram above, it is most convenient to rotate the entire cone about the $\begin{align*}y\end{align*}$ axis until the left side of the cone is vertical, then intersect it with a vertical plane perpendicular to the $\begin{align*}x-\end{align*}$ axis. Such a rotation leaves the $\begin{align*}y-\end{align*}$ variable unchanged. To see what it does to the $\begin{align*}x\end{align*}$ and $\begin{align*}z\end{align*}$ variables, let’s see what happens to the point $\begin{align*}(x,z)\end{align*}$ on the $\begin{align*}xz-\end{align*}$ plane when it is rotated by an angle of $\begin{align*}\theta\end{align*}$ .
::考虑这个锥体与上面图中标注的线线I的平行平面的交叉点,最方便的做法是在锥体左侧垂直之前在整个圆轴上旋转整个锥体,然后与垂直平面相交,与x-轴垂直。这样的旋转使 y- 可变不变的平面保持不变。要查看它对于 x 和 z 变量的作用,让我们看看 xz- 平面上的点(x,z) 发生什么,当它被一个角度旋转时, xz- 平面上的点(x,z) 会发生什么。

播放段落

In the above diagram, $\begin{align*}P(x,z)\end{align*}$ is rotated by an angle of $\begin{align*}\theta\end{align*}$ to the point $\begin{align*}P'\end{align*}$ . We have marked the side lengths $\begin{align*}QP = x\end{align*}$ and $\begin{align*}SQ = z\end{align*}$ . By the Pythagorean theorem, $\begin{align*}SP = \sqrt{x^2 + z^2}\end{align*}$ . We also have $\begin{align*}SP' = \sqrt{x^2 + z^2}\end{align*}$ , since rotation leaves the distance from the origin unchanged. To find the $\begin{align*}x-\end{align*}$ coordinates of our rotated point $\begin{align*}P'\end{align*}$ , we can use the fact that $\begin{align*}\cos(90 - \alpha - \theta) = \frac{SQ'}{\sqrt{x^2 + z^2}}\end{align*}$ . But by properties of cosine we have:
::在上述图表中, P( x, z) 由 角度旋转到 P 点。 我们已经标记了 QP =x 和 S z 的侧边长度 。 通过 Pythagorean 定理, SP =x2+z2, 我们也有 SP =x2+z2, 因为旋转离原点的距离没有改变 。 要找到旋转点 P 的 x 坐标, 我们可以使用 cos( 90 ) = S x2+z2 的特性。 但是根据 cosine 的特性, 我们可以看到 :

播放段落

$$\begin{align*}\cos(90 - \alpha - \theta) = \sin(\alpha + \theta),\end{align*}$$
::COs( 90) =sin ,

播放段落

and substituting with the sine addition formula gives us:
::并用必备附加公式取代我们:

播放段落

$$\begin{align*}\frac{SQ'}{\sqrt{x^2 + z^2}} = \sin(\alpha) \cos(\theta) + \cos(\alpha) \sin(\theta),\end{align*}$$
::Sx2+z2=sin(α)cos()+cos(α)sin(),

播放段落

which we can use our diagram to change to:
::我们可以用我们的图表将其修改为:

播放段落

$$\begin{align*}\frac{SQ'}{\sqrt{x^2 + z^2}} = \frac{x}{\sqrt{x^2 + z^2}} \cos(\theta) + \frac{z}{\sqrt{x^2 + z^2}} \sin(\theta)\end{align*}$$
::x2+z2=xx2+z2cos()+zx2+z2sin()

播放段落

which simplifies to:
::简化为:

播放段落

$$\begin{align*}SQ' = x \cos(\theta) + z \sin(\theta)\end{align*}$$
::xcos+zsin

播放段落

To find the $\begin{align*}x-\end{align*}$ coordinates of our rotated point $\begin{align*}P'\end{align*}$ , we can use the fact that $\begin{align*}\sin(90 - \alpha - \theta) = \frac{P' Q'}{\sqrt{x^2 + z^2}}\end{align*}$ . But by properties of sine we have:
::为了找到我们旋转点P的x- 坐标, 我们可以使用罪( 90) = Px2+z2 这一事实, 但是根据正弦的属性, 我们拥有 :

播放段落

$$\begin{align*}\sin(90 - \alpha - \theta) = \cos(\alpha + \theta)\end{align*}$$
:90)=cos()

播放段落

and substituting with the cosine addition formula gives us:
::并用余弦加法替代 给我们提供了:

播放段落

$$\begin{align*}\frac{P' Q'}{\sqrt{x^2 + z^2}} = \cos(\alpha) \cos(\theta) - \sin(\alpha)\sin(\theta),\end{align*}$$
::Px2+z2=cos(α)cos()-sin(α)sin(),

播放段落

which we can use our diagram to change to:
::我们可以用我们的图表将其修改为:

播放段落

$$\begin{align*}\frac{P' Q'}{\sqrt{x^2 + z^2}} = \frac{z}{\sqrt{x^2 + z^2}} \cos(\theta) - \frac{x}{\sqrt{x^2 +z^2}} \sin(\theta)\end{align*}$$
::Px2+z2=zx2+z2cos()-xxx2+z2sin()

播放段落

which simplifies to:
::简化为:

播放段落

$$\begin{align*}P'Q'=z \cos(\theta) - x \sin(\theta)\end{align*}$$
::Pzcos -xsin Name

播放段落

Looking back at the picture, this means that the coordinates of $\begin{align*}P'\end{align*}$ are $\begin{align*}(x \cos(\theta) + z \sin(\theta), \ z \cos(\theta) - x \sin(\theta))\end{align*}$ . In other words, in rotating from $\begin{align*}P\end{align*}$ to $\begin{align*}P'\end{align*}$ , the $\begin{align*}x-\end{align*}$ coordinate changes to $\begin{align*}x \cos(\theta) + z \sin(\theta)\end{align*}$ and the $\begin{align*}z-\end{align*}$ coordinate changes to $\begin{align*}z \cos(\theta) - x \sin(\theta)\end{align*}$ .
::回过头来,这意味着P的坐标是(xcos()+zsin(),zcos()-xsin())。 换句话说,在从P旋转到P ' 时,对 xcos()+zsin()的X-坐标修改和z-对zcos()-xsin()的坐标修改。

播放段落

If this rotation happens to every point on the cone, we can substitute $\begin{align*}x \cos(\theta) + z \sin(\theta)\end{align*}$ for $\begin{align*}x\end{align*}$ and $\begin{align*}z \cos(\theta) - x \sin(\theta)\end{align*}$ for $\begin{align*}z\end{align*}$ into our equation of the cone, resulting in a new equation for the cone after rotating by $\begin{align*}\theta\end{align*}$ .
::如果这种旋转发生在锥体的每一个点上, 我们可以用 x+zsin 代替 x 和 zcos-xsin 代替 z 以 z) 代替 z 以 z) 取代 锥体的方程, 从而在 + 旋转后为锥体产生一个新的方程 。

播放段落

$$\begin{align*}(x \cos(\theta) + z \sin(\theta))^2 + y^2 & = a^2(z \cos(\theta) - x \sin(\theta))^2 \\ x^2 \cos^2(\theta) + 2xz \cos(\theta) \sin(\theta) + z^2 \sin^2(\theta) + y^2 & = a^2(x^2 \sin^2(\theta) - 2xz \cos(\theta) \sin(\theta) + z^2 \cos^2(\theta)) \\ x^2 \cos^2(\theta) + 2xz \cos(\theta) \sin(\theta) + z^2 \sin^2(\theta) + y^2 & = a^2 x^2 \sin^2(\theta) - 2a^2 xz \cos(\theta) \sin(\theta) + a^2 z^2 \cos^2(\theta)) \\ x^2 \cos^2(\theta) + 2xz \cos(\theta) \sin(\theta) + z^2 \sin^2(\theta) + y^2 & = a^2 x^2 \sin^2(\theta) - 2a^2 xz \cos(\theta) \sin(\theta) + a^2 z^2 \cos^2(\theta))\end{align*}$$
:xco+zsins) 2+y2=a2(z222x2+2x克斯科2x+2x克斯科2+2x科斯+y2+()+()+()+()+ + + )( + ) + 2 + 2 ) + ( + + 2)( + + + + x ) + ( + ( + ( + ) ( + ( +

播放段落

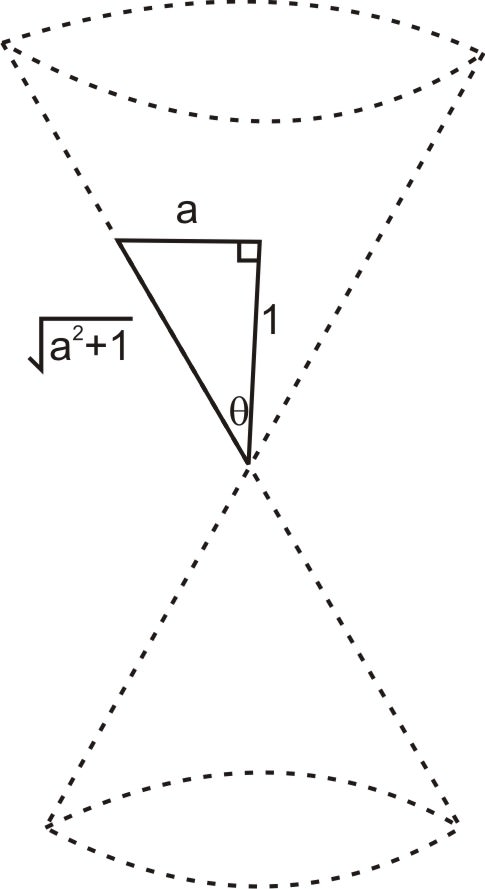
Now in the case of the tilted cone, we want to tilt the cone such that the left side becomes vertical. Since the factor $\begin{align*}a\end{align*}$ determines how tilted the cone is, we can see from the triangle below that $\begin{align*}\sin(\theta) = \frac{a}{\sqrt{1 + a^2}}\end{align*}$ and $\begin{align*}\cos(\theta) = \frac{1}{\sqrt{1 + a^2}}\end{align*}$ .
::现在,对于倾斜的锥体,我们想倾斜锥体,使左侧变成垂直。既然一个因素决定锥体是如何倾斜的,我们可以从犯罪()=a1+a2和cos()=11+a2下的三角体中看到。

播放段落

So the equation becomes:
::等式变成:

播放段落

$$\begin{align*}x^2 \frac{1}{1 + a^2} + 2xz \frac{a}{1 + a^2} + z^2 \frac{a^2}{1 + a^2} + y^2 & = a^2 x^2 \frac{a^2}{1 + a^2} - 2a^2 xz \frac{a}{1 + a^2} + a^2 z^2 \frac{1}{1 + a^2} \\ x^2 + 2xza + z^2 a^2 + y^2(1 + a^2) & = a^4 x^2 - 2a^3xz + a^2 z^2 \\ x^2 + 2xza + y^2(1 + a^2) & = a^4 x^2 - 2a^3 xz\end{align*}$$
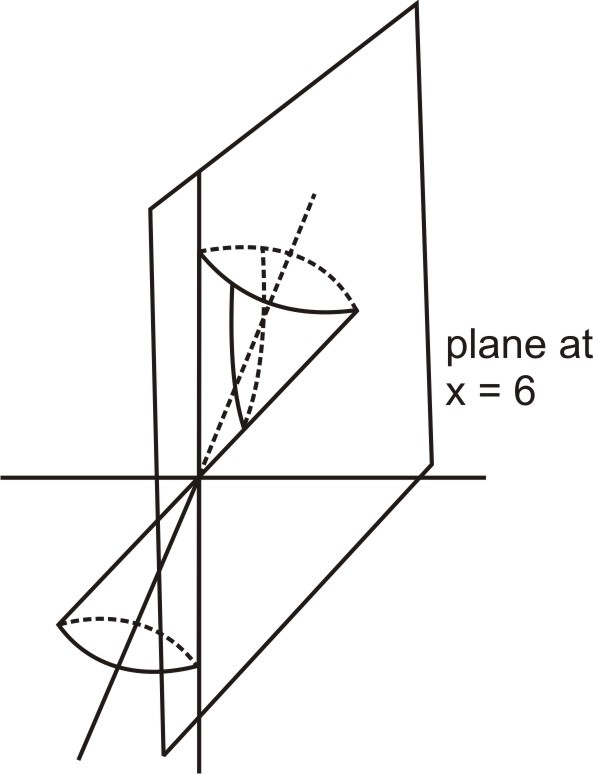
::x211+a2+2xza1+a2+2xZ2+a2+a2+y2=a2x2a21+a2+a2-2a2xxza1+a2+a2+a2+a2x2x2+x2xZ2+Z2a2+y2(1+a2)=a4x2-2a3x2+a2x2xx2+a2+Z2a2+a2+y2+y2=a2x2a2+a2x2xx2xxx2+Z2+Z2a2+Z2+++A2x2+y2(1+a2+a2+a2+a2xa2+A2+y2(1+a2)=a4x2-a3x+x2x2x+a2x2x2x2x2+a2x2=a4x2x2+x2x2x2x2x2x2x2x2

播放段落

Now that we have tilted our cone, to take a cross section that is parallel to the left side of the cone, we can simply cut it with a vertical plane. The equation of a vertical plane going through $\begin{align*}(b,0,0)\end{align*}$ and perpendicular to the $\begin{align*}x-\end{align*}$ axis is $\begin{align*}x = b\end{align*}$ . Therefore, setting $\begin{align*}x\end{align*}$ equal to the constant in the equation above will give us the intersection of the tilted cone and a plane parallel to one side of the cone. $\begin{align*}b\end{align*}$ . Here is a picture of the rotation and the cross-section, which lies in an $\begin{align*}xz-\end{align*}$ plane.
::现在,我们已经倾斜了我们的锥体, 取一个与锥体左侧平行的横截面, 我们可以用垂直平面剪切它。 垂直平面经过( b, 0, 0) 且与 x - 轴垂直的方程是 x=b 。 因此, 在方程中设置 x 等同于常数, 将会给我们提供倾斜锥体的交叉点, 和锥体一侧平行的一平面 。 b. 这是旋转和交叉面的图片, 位于 xz- 平面上 。

播放段落

Setting $\begin{align*}x\end{align*}$ equal to the constant $\begin{align*}b\end{align*}$ , we have:
::设置 x 等于常数 b, 我们有:

播放段落

$$\begin{align*}b^2 + 2abz + y^2(1 + a^2) & = a^4 b^2 - 2a^3 bz \\ z(2ab + 2a^3 b) & = -y^2(1 + a^2) +a^4 b^2 - b^2 \\ z & =\left (\frac{-1 - a^2}{2ab + 2a^3 b}\right )y^2 + (a^4 b^2 - b^2)\end{align*}$$
::b2+2ABZ+y2(1+a2)=a4b2-2-2a3bzz(2ab+2a3b)y2(1+a2)+a4b2-b2z=(1-a22ab+2a3b)y2+(a4b2-b2)

播放段落

Although this coefficient and constant term seem complicated, $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ can be chosen so that the coefficient of the $\begin{align*}y^2\end{align*}$ term can be equal to any number (you will explore this fact in an exercise). The constant term can be ignored since any parabola can be shifted vertically by any amount.
::尽管这个系数和常数似乎很复杂,但可以选择一个和b,这样y2术语的系数可以与任何数字相等(你可以在练习中探讨这一事实 ) 。 常数可以忽略,因为任何抛物线都可以以任何数量垂直移动。

播放段落

So the general form of a parabola is:
::因此,抛物线的一般形式是:

播放段落

$$\begin{align*}z = Ay^2\end{align*}$$
::z z = Ay2

播放段落

where $\begin{align*}A\end{align*}$ is any constant.
::其中 A 是 常数 。

播放段落

Or, using the more standard $\begin{align*}x-\end{align*}$ and $\begin{align*}y-\end{align*}$ coordinates the form of a parabola is
::或者,使用更标准的 x - 和 Y - 坐标, 抛物线的形式就是

播放段落

$$\begin{align*}y = ax^2\end{align*}$$
::y=ax2 y=ax2 y=ax2

播放段落

As before, this equation can be adapted to produce the shifted and horizontally oriented forms.
::与以往一样,这一等式可以调整,以产生变化式和横向式的形式。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked a question about Brandyn, who is unsure why he has a y ² term in his standard form  equation instead of an x ² term.
::早些时候,有人问你一个有关Brandyn的问题,谁不知道为什么他的标准形式方程式中有一个Y2条件,而不是x2条件。

播放段落

Brandyn keeps coming up with a y ² term because this is a sideways parabola.
::Brandyn不断想出一个Y2术语, 因为这是一个侧路抛物线。

播放段落

Example 2
::例2

播放段落

In the proof above, we greatly simplified the formula near the end by substituting A for $\begin{align*}\frac{-1 -a^2}{2ab + 2a^3 b}\end{align*}$ .
::在以上证据中,我们大大简化了接近尾声的公式,用A替代1-a22ab+2a3b。

播放段落

Explain why this was permissible by showing that for any $\begin{align*}A\end{align*}$ there exist constants $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ such that $\begin{align*}A = \frac{-1 -a^2}{2ab + 2a^3 b}\end{align*}$ .
::说明为何允许这样做,说明对于任何A类而言,都存在a和b常数,如A1-a22ab+2a3b。

播放段落

Solving for $\begin{align*}b\end{align*}$ in terms of $\begin{align*}A\end{align*}$ and $\begin{align*}a\end{align*}$ , we have:

$$\begin{align*}A(2ab + 2a^3 b) & = -1 - a^2 \\ 2Aab(1 + a^2) & = -(1 +a^2) \\ 2 Aab & = -1 \\ 2Aab & = -1 \\ b & = -\frac{1}{2Aa}\end{align*}$$ So we can set $\begin{align*}b=2Aa\end{align*}$ and the relationship will hold.
::从A和A的角度来看,我们有:A(2ab+2a3b)1-a22Aab(1+a2)2Aab*12Aab*12Aab*1b12Aa,这样我们就可以确定b=2Aa,关系将维持下去。

播放段落

Example 3
::例3

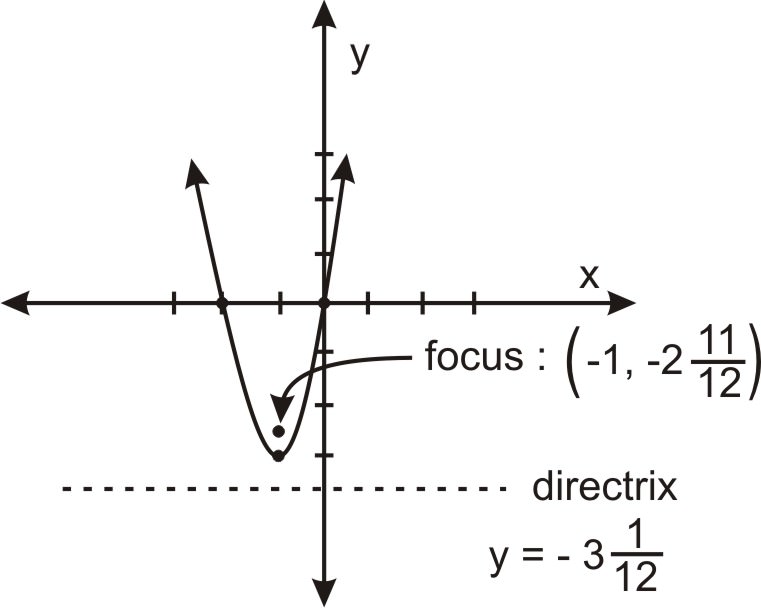
播放段落

Draw a sketch of the following parabola. Also identify its directrix and focus. $\begin{align*}3x^2 + 6x - y = 0\end{align*}$
::绘制以下抛物线的草图。 还要指定其直线和焦点 。 3x2+6x-y=0

播放段落

Factor and complete the square to get: $\begin{align*}3(x + 1) = y + 3\end{align*}$ . The vertex is at: $\begin{align*}(-1, -3)\end{align*}$ .
::系数并完成正方形以获得 : (3x+1) =y+3 。 顶点为 (-1) -3 。

播放段落

The focus is $\begin{align*}(-1, -2 \frac{11}{12})\end{align*}$ The directrix is the line $\begin{align*}y = -3 \frac{1}{12}\end{align*}$
::焦点是(-1,-21112) 直线是 y3112

播放段落

Example 4
::例4

播放段落

Find the equation for a parabola with directrix $\begin{align*}y=-2\end{align*}$ and focus (3,8).
::找到一个配有 y2 和焦点( 3, 8) 的抛物线的方程。

播放段落

The vertex is vertically midway between the focus and directrix: $\begin{align*}\frac {-2 + 8}{2} = 3\end{align*}$ , the same horizontally as the focus: $\begin{align*}x = 3\end{align*}$ and therefore at: $\begin{align*}(3, 3)\end{align*}$ .
::顶部位于焦点和直线之间的垂直中点:-2+82=3,与焦点水平相同:x=3,因此在(3 3)处。

播放段落

Substituting those values into the formula gives:
::在公式中将这些数值替换为:

播放段落

$\begin{align*}y - 3 = \frac{1}{20}(x -3)^2\end{align*}$
::y-3=120(x-3)2

播放段落

Example 5
::例5

播放段落

Find the equation for a parabola with directrix $\begin{align*}y = 3\end{align*}$ and focus (2, -1).
::查找具有 y=3 和 聚焦点 (2, - 1) 的 抛物线的方程。

播放段落

Using the vertex form of a parabola $\begin{align*}(y - k)^2 = 4a(x - h)\end{align*}$ :
::使用抛物线(y-k)2=4a(x-h)的顶点形式:

播放段落

Recall that the vertex y-value $\begin{align*}k\end{align*}$ is the midpoint of the directrix and the focus on the line perpendicular to the directrix and crossing the focus. Therefore the y-value of the vertex is $\begin{align*}1\end{align*}$
::提醒注意顶点 y 值 k 是指向的中点, 以及重心与直线垂直的直线和越过焦点的焦点。 因此顶点的 Y 值是 1 。

播放段落

Recall that the vertex x-value $\begin{align*}h\end{align*}$ is the same as the focus, therefore the vertex x-value is $\begin{align*}2\end{align*}$
::提醒注意,顶点X值 h 与焦点相同,因此,顶点X值为 2

播放段落

Finally, recall that $\begin{align*}a\end{align*}$ the distance from the vertex to the focus or from the vertex to the directrix (which are the same): $\begin{align*}\therefore a = 2\end{align*}$
::最后,请记住从顶端到焦点的距离,或从顶端到直线的距离(相同):a=2

播放段落

Substituting gives: $\begin{align*}(y - 1)^2 = 8(x - 2) \to y^2 +1 = 8x -16 \to y^2 = 8x -17\end{align*}$
::替代给定值 : (y- 1) 2= 8( x-2) y2+1= 8x-16_y2=8x-17

播放段落

Example 6
::例6

播放段落

Describe the shape of a parabola as it relates to a cone or double cone.
::描述与锥形或双锥形相关的抛物线的形状。

播放段落

The shape of a parabola as it relates to a cone or double cone, is that a parabola represents the revealed shape when a hollow cone is sliced through at an angle equal to the side of the cone. Particularly clear with a double cone is the fact that slicing through at a steeper angle will result in two curves (a hyperbola) and a shallower angle will result in an ellipse.
::抛物线的形状与锥形或双锥形有关,是当空锥形被切成与锥形对等的角时,抛物线代表显露的形状。 特别明显的是,双锥形的形状是,在陡峭角切成两个曲线(一个双曲线),而浅角的形状则会导致椭圆。

播放段落

Example 7
::例7

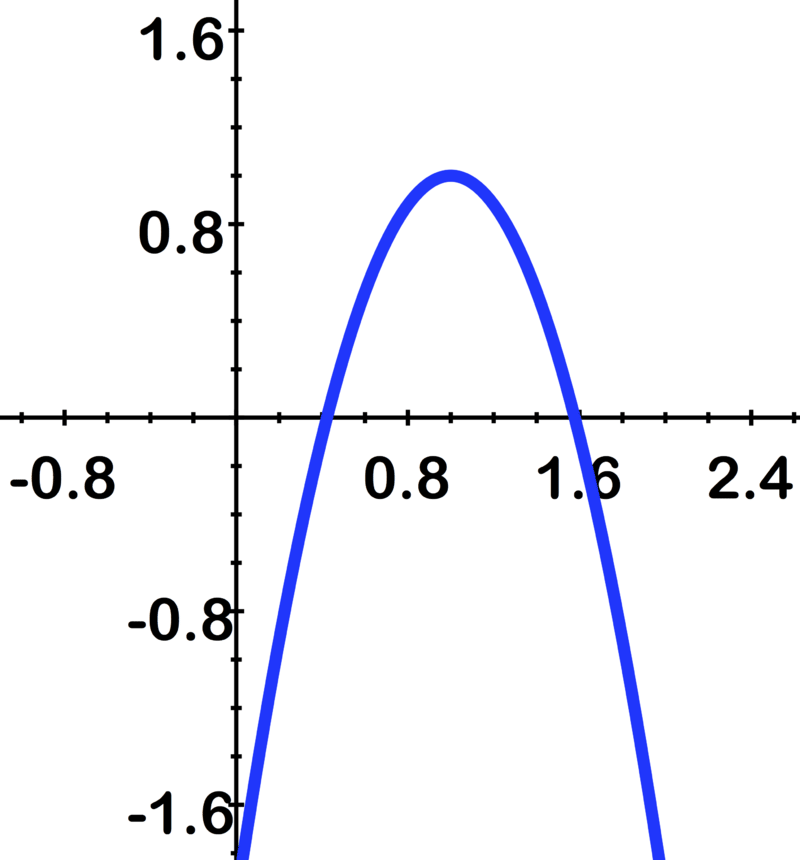
播放段落

Sketch the following parabola and identify the directrix and focus:  $\begin{align*}4x^2 -3x +y = 7\end{align*}$ .
::绘制以下抛物线并确定直线和焦点:4x2-3x+y=7。

播放段落

$\begin{align*}y = ax^2 + bx + c\end{align*}$ ..... Recall the standard form of a parabola
::y=ax2+bx+c .... 。 提醒注意抛物线的标准格式

播放段落

$\begin{align*}a = -3 | b = 6 | c = -2\end{align*}$ ..... Extract a, b, c
::3b=6c2...。 摘录 a, b, c

播放段落

$\begin{align*}x = \frac{-6}{2(-3)} \to x = 1\end{align*}$ ..... The x-coordinate of the vertex = $\begin{align*}\frac{-b}{2a}\end{align*}$
::x62(- 3) x= 1 .... 顶部的 x 坐标 =- b2a

播放段落

$\begin{align*}y = (-3)(1) + 6(1) -2\end{align*}$ ..... Substitute the calculated x-value to solve for y
::y=(-3)(1)+6(1)-2-...。替换y 的计算 X 值。

播放段落

$\begin{align*}y = 1\end{align*}$ ...... The vertex = $\begin{align*}(1, 1)\end{align*}$
::y=1.................. 顶部 =(1,1)

播放段落

$\begin{align*}x = 1\pm\frac{1}{\sqrt{3}}\end{align*}$ ..... Identify the x-intercepts using the Quadratic Formula
::x=113...。 使用二次曲线公式来识别 x 界面 。

播放段落

Review
::回顾

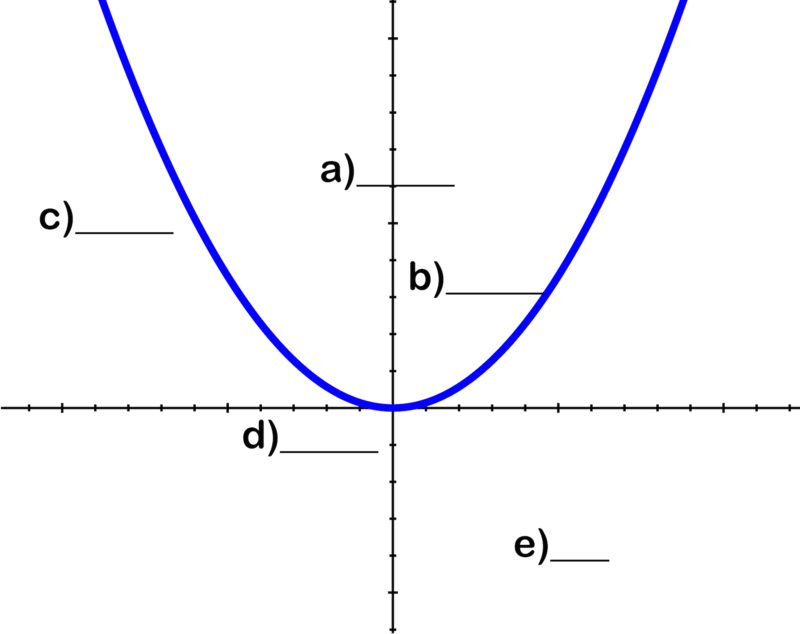
播放段落

Use the image to identify the parts of the parabola:
::使用图像来识别抛物线的部分 :

播放段落
1. The Focus
   ::焦点
播放段落
2. The Vertex
   ::顶点
播放段落
3. The Focal Radius
   ::焦半径
播放段落
4. The Directrix
   ::导演
播放段落
5. The Parabola
   ::帕拉波拉

播放段落

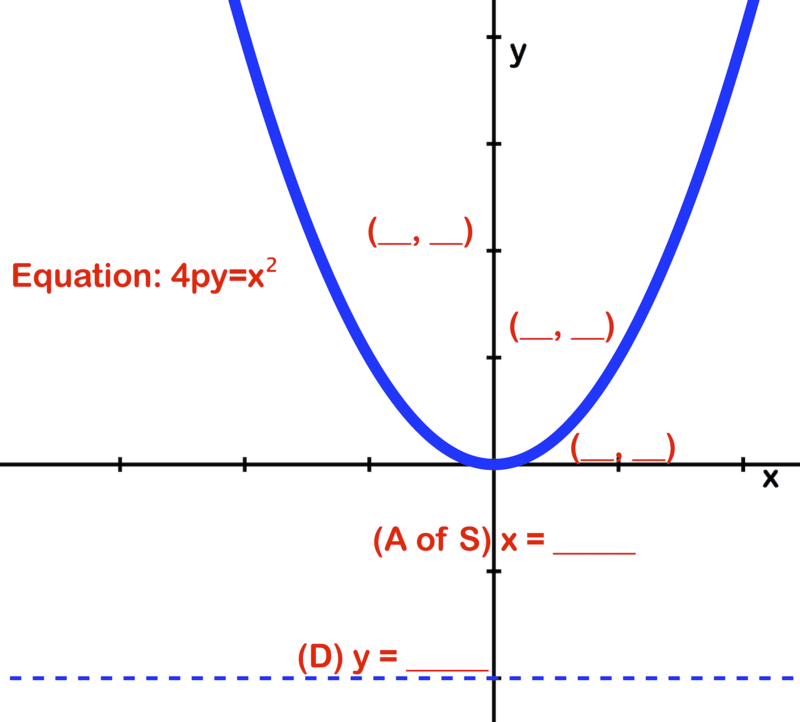
Use the image and given equation of the parabola to identify the following:
::使用抛物线的图像和给定方程式来识别以下内容:

播放段落
6. The coordinates of the focus
   ::焦点坐标
播放段落
7. The equation of the directrix
   ::直线方程式的方程式
播放段落
8. The length of the focal radius
   ::焦半径长度
播放段落
9. The equation of the axis of symmetry
   ::对称轴的方程
播放段落
10. The coordinates of the vertex
    ::顶部坐标

播放段落
11. Find the equation for a parabola with directrix: $\begin{align*}x = 2\end{align*}$ and focus: $\begin{align*}(0, -2)\end{align*}$
    ::查找有直接轴:x=2和焦点0)-2的抛物线的方程
播放段落
12. Find the equation for a parabola with vertex: $\begin{align*}(5, -2)\end{align*}$ and directrix: $\begin{align*} y = -5\end{align*}$
    ::查找有顶层( 5) 和直线: y @% 5 的抛物线的方程
播放段落
13. Find the equation for a parabola with focus: $\begin{align*}(3, 5)\end{align*}$ and vertex: $\begin{align*}(3, 1)\end{align*}$
    ::查找焦点为( 3, 5) 和顶点为( 3, 1) 的抛物线方程

播放段落

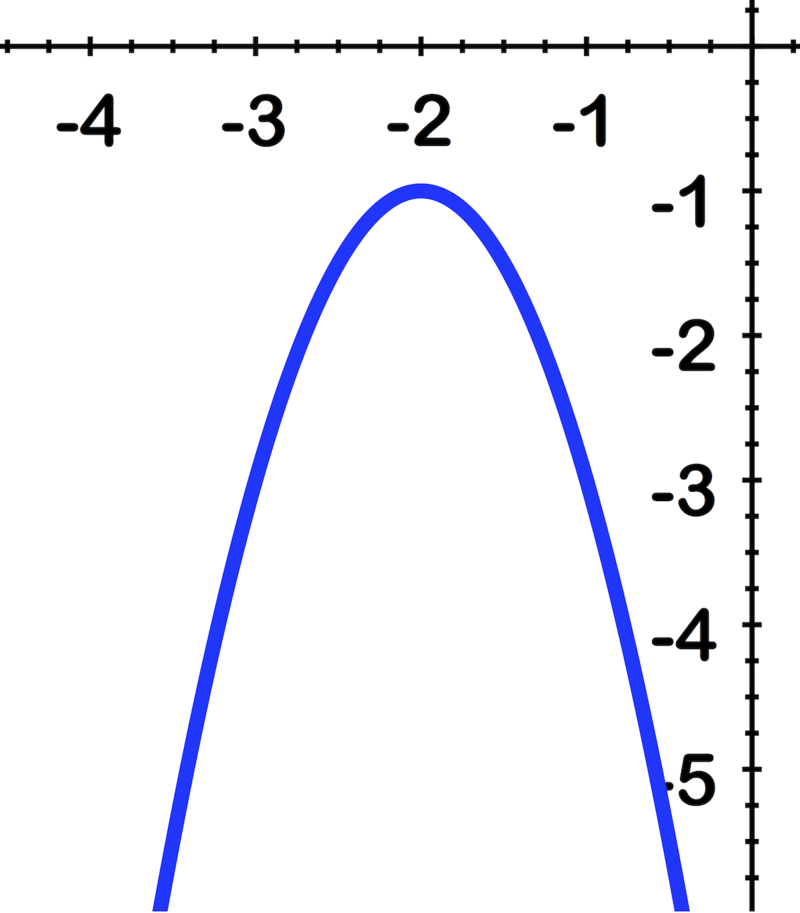
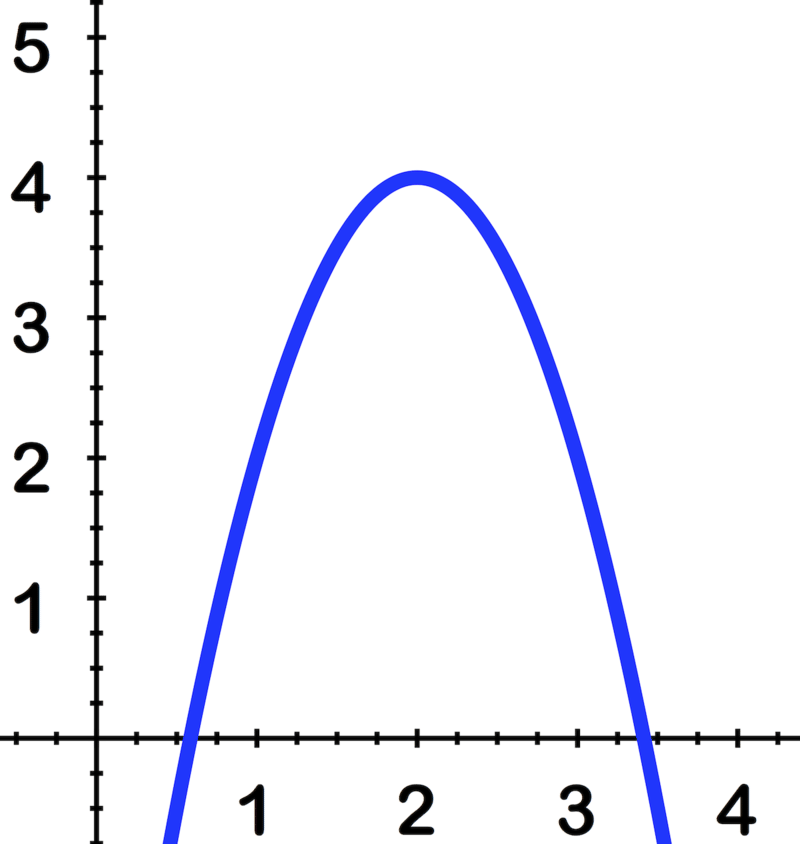
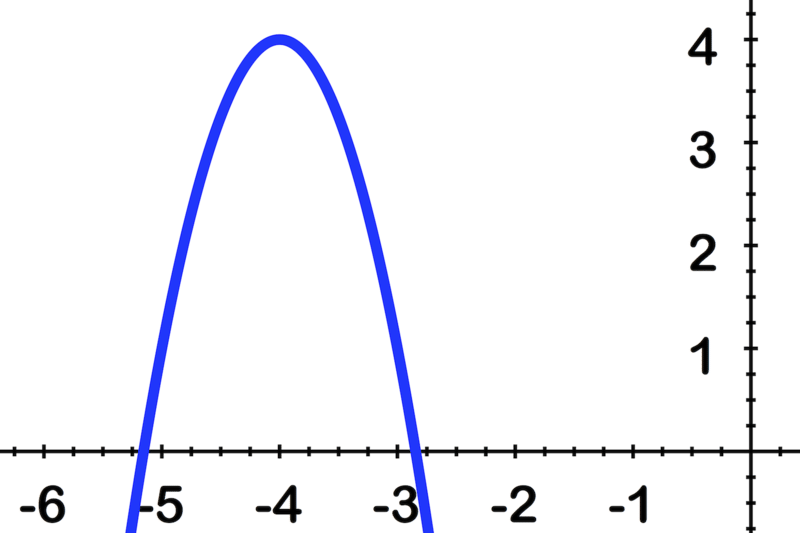
Use the image to identify the vertex, axis of symmetry and equation of the parabola:
::使用图像来识别抛物线的顶部、对称轴和方程:

14. 
15. 
16. 

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。

 

播放段落

Resources
::资源