锥形块和丹德林球体

播放段落

One of the major activities of mathematicians and scientists of all kinds is learning, and attempting to prove, how and why things work.
::数学家和各种科学家的主要活动之一是学习,试图证明事情是如何和为什么起作用的。

播放段落

Since Ancient Greece at the beginning of the millennium, and likely well before, the properties of have been studied. One that has been explored extensively is the "Focal Property", which we have referred to in nearly every lesson in this section.
::自千年之初古希腊(古希腊)开始并可能在很早以前就已经研究过它的财产。 已经广泛探讨的一个问题是“殖民地财产 ” ( Focial Property),我们在本节的几乎所有教训中都提到了这个概念。

播放段落

There are a number of mathematical proofs of the focal property, but trying to explain such proofs to someone who does not dedicate his or her life to mathematics is difficult. The Dandelin Spheres are one solution.
::中心属性有许多数学证明,但很难向不把一生用于数学的人解释这些证明。 Dandelin Spheres是一个解决方案。

播放段落

Conic Sections and Dandelin Spheres
::锥形块和丹德林球体

播放段落

Dandelin Spheres and the Equation of an Ellipse
::Dandelin 球体和椭圆的等分

播放段落

It wasn’t until 1822 that the French mathematician Germinal Dandelin thought of this very clever construction. Dandelin found a way to find the foci and prove the focal property in one fell swoop.
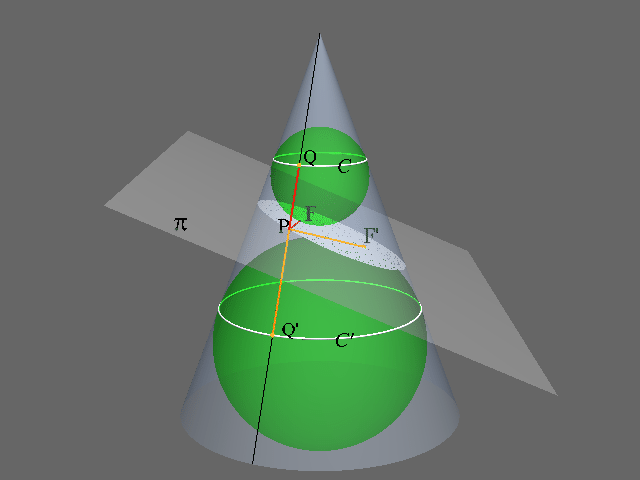
::直到1822年,法国数学家Germinal Dandelin才想到了这个非常聪明的建筑。 Dandelin找到了找到福西的方法,并证明了其中的焦点财产。

播放段落

Take the conic section in question. Then choose a sphere that is just the right size so that when it’s dropped into the conic, it touches the intersecting plane, as well as being snug against the cone on all sides. If you prefer, you can think of the sphere as a perfectly round balloon that is blown up until it “just fits” inside the cone, still touching the plane. Then do the same on the other side of the plane. After we’ve drawn both of these spheres we have this picture:
::选一个正方形的圆锥形区域。 然后选择一个刚好是正方形的球体, 以便当球体掉入二次曲线时, 球体会触动交错的平面, 并且对锥形各侧的球体进行纠缠。 如果您愿意的话, 你可以把球体看作是一个完美的圆球球, 直到球体在锥形内“ 正好合身 ” 时, 球体仍然会触动飞机。 然后在另一侧的飞机上做同样的操作。 在我们绘制了这两个球体之后, 我们拍了这张图:

播放段落

or
::或

播放段落

These spheres are often called “Dandelin spheres”, named after their discoverer. It turns out that not only is our shape an ellipse (which, like all satisfies the focal property), but these spheres touch the ellipse exactly at the two foci. To see this, consider this geometric argument.
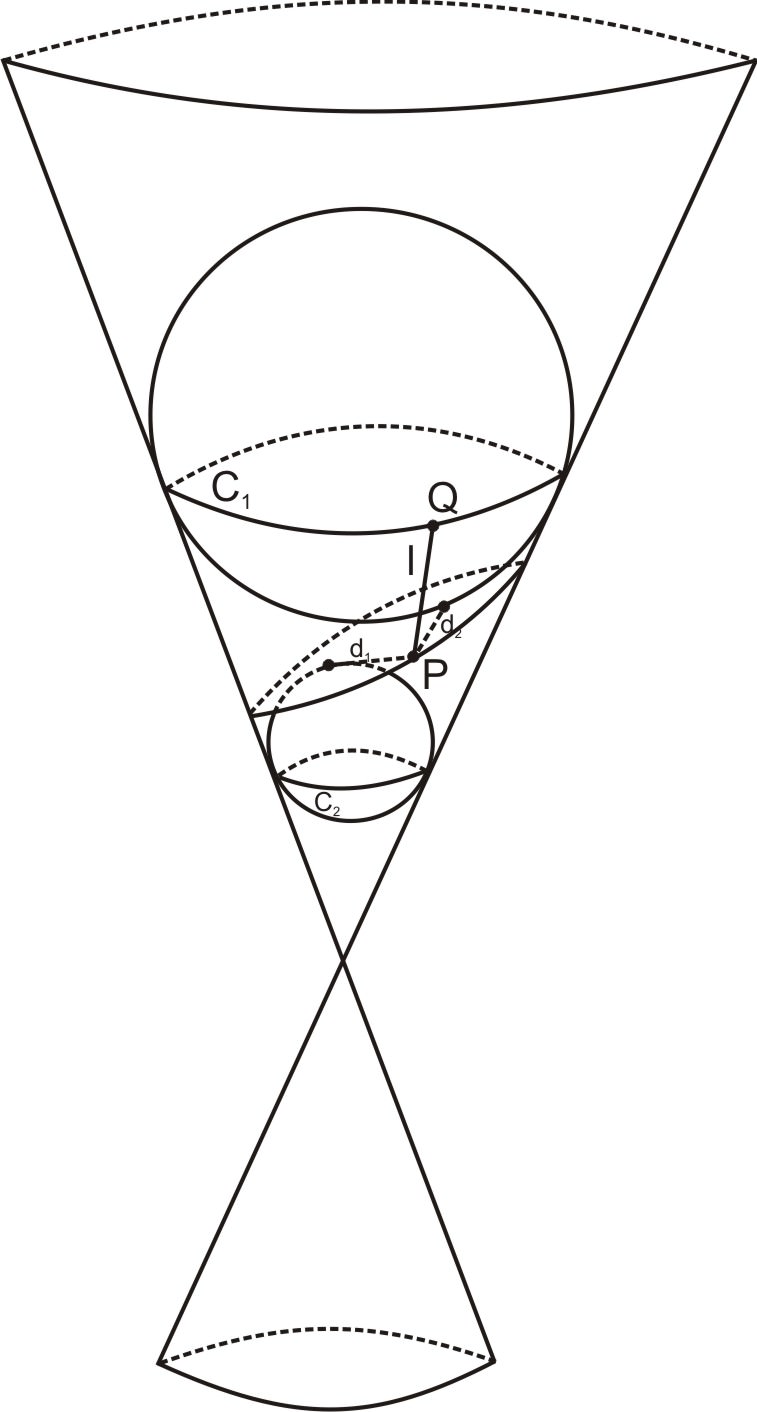
::这些球体通常被称为“丹德林球体 ” , 以其发现者命名。 事实证明,不仅我们的形状是椭圆形(像所有球体一样满足核心特性 ) , 这些球体触碰了椭圆形, 恰好在两个方块上。 要看到这一点, 请考虑这个几何参数。

播放段落

The first thing to notice is that the circles $\begin{align*}C_1\end{align*}$ and $\begin{align*}C_2\end{align*}$ shown on the diagram below, where each sphere lies snug against the cone, lie in parallel planes to one another. In particular, each line passing through these circles and the vertex of the cone, such as the line $\begin{align*}l\end{align*}$ drawn below, cuts off equal segments between the two circles. Let's call $\begin{align*}d\end{align*}$ the shortest distance along the cone between circles $\begin{align*}C_1\end{align*}$ and $\begin{align*}C_2\end{align*}$ . This can also be thought of as the shortest distance between $\begin{align*}C_1\end{align*}$ and $\begin{align*}C_2\end{align*}$ that passes through the vertex of the cone.
::首先需要注意的是,下图中显示的圆圈C1和C2,每个球体在圆锥上相互粘结,位于平行的平面上。特别是,每条横穿这些圆圈的线和圆锥的顶端,例如下面的线,截断两个圆圈之间的相等部分。我们称之为圆锥C1和C2之间的最短距离。这也可以被认为是穿过圆锥的顶端的C1和C2之间的最短距离。

播放段落

The next thing to remember is a property of tangents to spheres that you may have learned in geometry. If two segments are drawn between a point and a sphere, and if the line containing each segment is tangent to the sphere, then the two segments are equal. In the diagram below, $\begin{align*}AB=AC\end{align*}$ . (This follows from the fact that tangents are perpendicular to the radii of a sphere and that two congruent triangles are formed in this configuration.)
::接下来要记住的是您在几何学学过的字段的正切属性。 如果在点和球间绘制两个区段, 如果每个区段的线条与球体相切, 那么两个区段是相等的。 在下图中, AB=AC 。 (这是因为正切值与球体的半径相切, 并且在此配置中形成两个相似的三角形 。)

播放段落

Now consider the point $\begin{align*}P\end{align*}$ on the ellipse drawn below. Let $\begin{align*}\overline{QR}\end{align*}$ be the segment of length $\begin{align*}d\end{align*}$ between $\begin{align*}C_1\end{align*}$ and $\begin{align*}C_2\end{align*}$ that passes through $\begin{align*}P\end{align*}$ . The distances between the two foci are marked $\begin{align*}d_1\end{align*}$ and $\begin{align*}d_2\end{align*}$ . But $\begin{align*}d_1 =RP\end{align*}$ and $\begin{align*}d_2 =PQ\end{align*}$ by the property of tangents to spheres discussed above. So $\begin{align*}d_1 + d_2 = RP + PQ = QR = d\end{align*}$ . And this sum will always equal $\begin{align*}d\end{align*}$ , no matter what point $\begin{align*}P\end{align*}$ on the ellipse is chosen. So this proves the : that the sum of the distances between any point on the ellipse and the two foci is constant.
::现在考虑下面所绘制的椭圆上的点P。 让 QR 成为通过 P 的 C1 和 C2 之间的长度段。 两个 foci 之间的距离标记为 d1 和 d2 。 但 d1 = RP 和 d2 = PQ 与上文讨论的域的正切属性。 因此, d1+d2 = RP+PR=d。 这个总和总是相等 d, 不管选择 extlipse 上的 P 点是哪个 。 因此, 这证明了 : 椭圆上任何点与两个 foci 之间的距离总和是恒定的 。

播放段落

Dandelin and the Parabola
::丹德林和帕拉波拉

播放段落

Like the ellipse, the parabola has a focal property. And, also like the ellipse, a construction similar to Dandelin’s with the spheres can show us what it is. Dandelin himself didn’t prove the focal property for that we are about to discuss, but Pierce Morton used a sphere construction similar to Dandelin’s to prove the focal property of parabolas in 1829. We’ll look at Morton’s argument here.
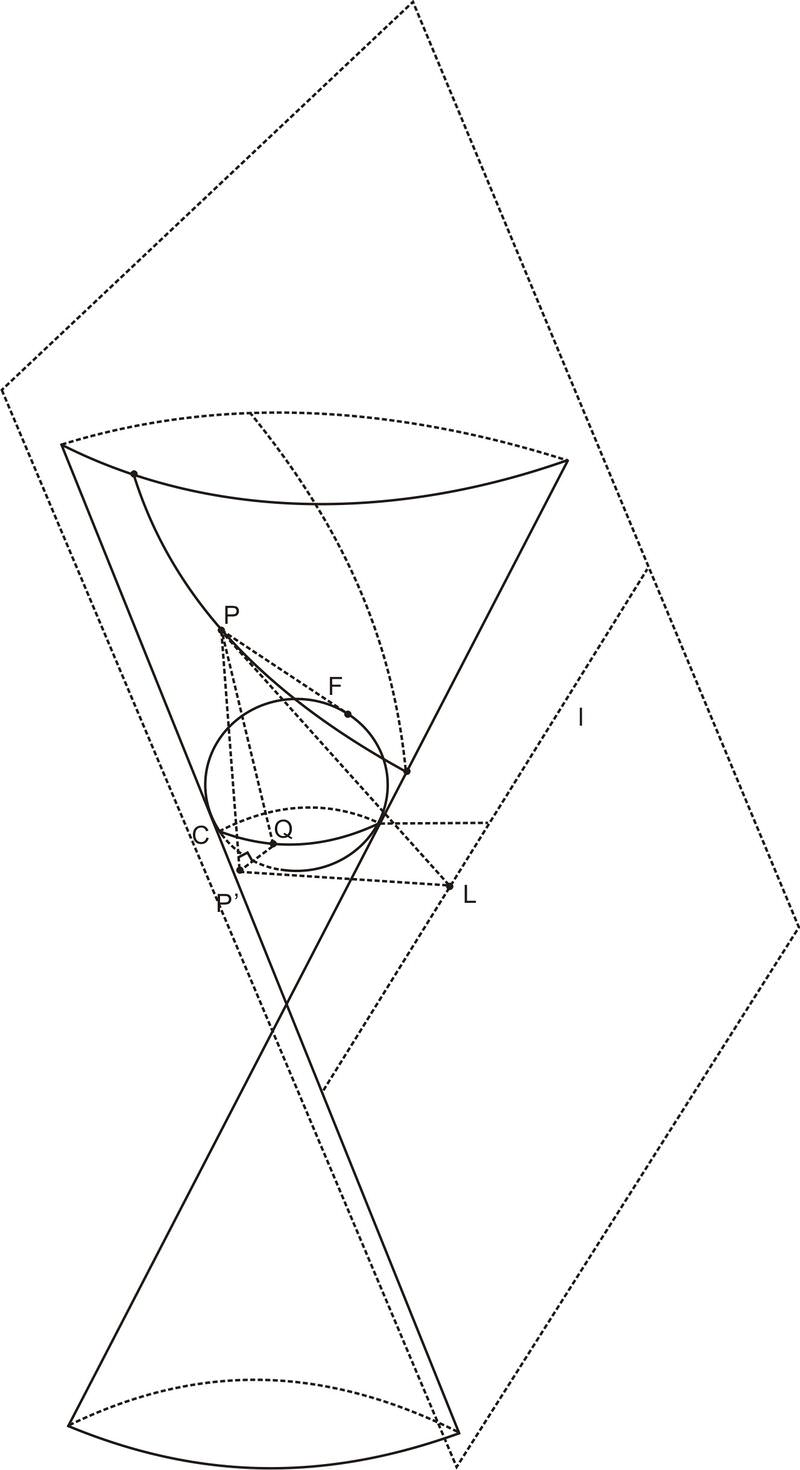
::与椭圆一样,抛物线也具有核心属性。 和椭圆一样,像丹德林(Dandelin)和球体一样的构造也向我们展示了它是什么。 丹德林(Dandelin)自己并没有证明我们即将讨论的焦点属性,但皮尔斯·莫顿(Pierce Morton)用类似于丹德林(Dandelin)的球体构造来证明1829年抛物线的核心属性。 我们在这里看看莫顿(Morton)的论点。

播放段落

In contrast with the argument we made for the ellipse, for a parabola we can only fit one tangent sphere inside the cone. That is, only one sphere can be tangent to both the cone and the cutting plane. In the diagram below, the sphere fits underneath the cutting plane, but there is no room for a sphere to lie on top of the cutting plane and still be tangent to the cone.
::与我们对椭圆的争论相反,对于一个抛物线来说,我们只能把一个相切的球体放在锥体内。也就是说,只有一个球体可以切换到锥体和切割机上。在下面的图表中,球体位于切割机下方,但是没有空间让球体放在切割机顶上,仍然切换到锥体上。

播放段落

As with the ellipse, the point where the sphere intersects the plane is called a focus . But because there is only one sphere in this construction, and this is related to the fact that a parabola has only one focus. The other geometric object of interest is called the directrix . This is the line that results from the intersection between the cutting plane and the plane that contains the circle of contact between the sphere and the cone. In the diagram below, the directrix is labeled $\begin{align*}l\end{align*}$ and is found by intersecting the plane defined by circle $\begin{align*}C\end{align*}$ and the cutting plane (the planes are shown in dashed lines for clarity). Finally, we will call the angle between the planes $\begin{align*}\theta\end{align*}$ .
::与椭圆一样, 球盘交叉的点点被称作焦点。 但是由于这个构造中只有一个球体, 这与抛物线只有一个焦点的事实有关。 另一个感兴趣的几何对象被称为直线。 这是切割机和圆锥体之间接触圈的平面之间的交叉点。 在下面的图表中, 直线被标为l, 并且通过将C圆和切割机定义的平面( 飞机以破折线显示以清晰度)交叉而发现。 最后, 我们将调用飞机之间的角 。

播放段落

In the above diagram, we have labeled the point where the sphere contacts the cutting plane with $\begin{align*}F\end{align*}$ , and we’ll call that point the focus of the parabola. Suppose $\begin{align*}P\end{align*}$ is an arbitrarily chosen point on the parabola. Then, let $\begin{align*}Q\end{align*}$ be the point on circle $\begin{align*}c\end{align*}$ such that $\begin{align*}\overline{P Q}\end{align*}$ is tangent to the sphere. In other words $\begin{align*}Q\end{align*}$ is chosen so that $\begin{align*}\overline{P Q}\end{align*}$ lies on the cone itself. Let $\begin{align*}L\end{align*}$ be the point on the directrix $\begin{align*}l\end{align*}$ such that $\begin{align*}\overline{P L}\end{align*}$ is perpendicular to $\begin{align*}l\end{align*}$ . Then $\begin{align*}PF = PQ\end{align*}$ since both segments are tangents to the sphere from the same point $\begin{align*}P\end{align*}$ . We can also show that $\begin{align*}PQ=PL\end{align*}$ . This follows from the fact that the cutting plane is parallel to one side of the cone. Consider the point $\begin{align*}P'\end{align*}$ that is the projection of $\begin{align*}P\end{align*}$ onto the plane containing circle $\begin{align*}C\end{align*}$ . Then $\begin{align*}\angle \ PP'Q\end{align*}$ and $\begin{align*}\angle \ PP'L\end{align*}$ are both right angles by the definition of a projection. $\begin{align*}\angle \ PQP'\end{align*}$ and $\begin{align*}\angle \ PLP'\end{align*}$ are both equal to the angle $\begin{align*}90 - \theta\end{align*}$ , where $\begin{align*}\theta\end{align*}$ is the angle defined above, because the cutting plane and the cone both have an angle of $\begin{align*}\theta\end{align*}$ with the horizon. Since they also share a side, triangles $\begin{align*}\triangle PQP'\end{align*}$ and $\begin{align*}\triangle PLP'\end{align*}$ are congruent by $\begin{align*}AAS\end{align*}$ . So the corresponding sides $\begin{align*}\overline{P Q}\end{align*}$ and $\begin{align*}\overline{P L}\end{align*}$ are congruent. By the transitive property we have $\begin{align*}PF=PL\end{align*}$ , so the distance between the point $\begin{align*}P\end{align*}$ on the parabola to the focus is the same as the distance between $\begin{align*}P\end{align*}$ and the directrix $\begin{align*}l\end{align*}$ . We have just proven the focus-directrix property of parabolas.
::在上图中, 我们标记了球体与 F 接触切割平面的点点, 然后我们会点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点点

播放段落

Dandelin Spheres and Hyperbolas
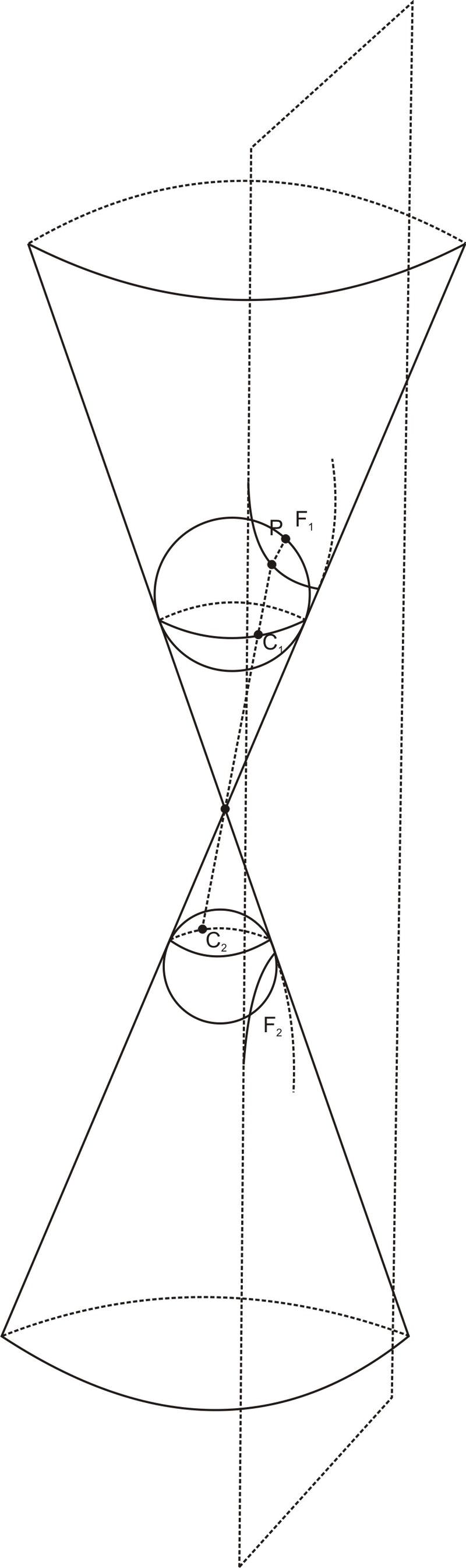
::Dandelin球体和超光谱

播放段落

To prove the focal property of , we examine Dandelin’s sphere construction. Unlike the construction for ellipses, which used two spheres on one side of the cone, and the sphere construction for parabolas, which used one sphere on one side of the cone, this construction uses two spheres, one on each side of the cone. As with the ellipse construction, each sphere touches the plane at one of the foci of the hyperbola. And as with the argument for the elliptical focal property, the argument uses the fact that tangents from a common point to a sphere are equal.
::为了证明丹德林的核心特性,我们检查了丹德林的球体构造。 与使用锥体一侧两个球体的椭圆形建筑和使用锥体一侧一个球体的螺旋形建筑不同,这种建筑使用锥体一侧一个球体的球体,使用锥体一侧两个球体。 与建造椭圆形一样,每个球体在超博的角上触碰飞机。 与对椭圆形财产的论点一样,这一论点使用了从一个共同点到一个球体之间的切线是平等的这一事实。

播放段落

In the above diagram, suppose $\begin{align*}P\end{align*}$ is an arbitrary point on the hyperbola. We would like to examine the difference $\begin{align*}PF_2 - PF_1\end{align*}$ . Let $\begin{align*}C_1\end{align*}$ be the point on the upper sphere that lies on the line between $\begin{align*}P\end{align*}$ and the vertex of the cone. Let $\begin{align*}C_2\end{align*}$ be the point on the upper sphere when this line is extended (so $\begin{align*}P\end{align*}$ , $\begin{align*}C_1\end{align*}$ , and $\begin{align*}C_2\end{align*}$ are all on the same line and $\begin{align*}PC_1 + C_1 C_2 = PC_2\end{align*}$ and the cone By the common tangent property, $\begin{align*}PF_1 = PC_1\end{align*}$ and $\begin{align*}PF_2 = PC_2\end{align*}$ for some points $\begin{align*}C_1\end{align*}$ and $\begin{align*}C_2\end{align*}$ on the circles where the spheres meet the cone. So $\begin{align*}PF_2 - PF_1 = PC_2 - PC_1 = (PC_1 + C_1 C_2) - PC_1 = C_1 C_2\end{align*}$ . But $\begin{align*}C_1 C_2\end{align*}$ is the distance along the cone between the two circles of tangency and is constant regardless of the choice of $\begin{align*}C_1\end{align*}$ and $\begin{align*}C_2\end{align*}$ . So the difference $\begin{align*}PF_2 - PF_1\end{align*}$ is constant.
::在上述图表中, 假设 P 是高球上的任意点 。 我们想对球体与锥体交汇的圆圈上某些点 C1 和 C2 的PF2 - PF1 和 C2 = PF2 = PPF1 和 C2 = PC2 的差点进行检查。 让 C1 成为 P 和锥体的顶部线上的上球点 。 当线线延伸时, 让 C2 成为上球的点 ( 所以 P1, C1, C2 和 C2 都在同一线上线上, PC2 和 PC2 = PF1 和 PPF2 = PC2 ) 。 所以 PF2 - PF2 - PF1 和 PF1 之间的差是恒定的。 因此, PF2 - PF1 和 PF1 的差是恒定的。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

What would the Dandelin spheres look like if used to explore a circle?
::丹德林的球体会是什么样子? 如果用来探索圆圈呢?

播放段落

Since the spheres touch the figure within just at the foci, and since a circle is an ellipse with both foci at the same point, the spheres would sit directly above each other, and would touch the circle at the center point on both sides.
::因为球体触摸到数字, 并且因为圆圈是一个椭圆形, 在同一点上, 两个球体都有一个角, 球体会直接坐在对方的上方, 并且会触动两边中心点的圆形。

播放段落

Example 2
::例2

播放段落

Conceptually speaking, why is there only one Dandelin Sphere used in the proof of a parabola?
::从概念上讲,为什么只有一个丹德林球体用于证明抛物线?

播放段落

As we learned in the proof for an ellipse, the Dandelin sphere must be tangent to both the cone, e.g., the sphere touches the cone all the way around in a circle, and the plane, where the tangency is a single point. In the case of a parabola, the sphere below the plane "fits" just fine, but a sphere above the plane would "sit on" the plane, and not touch the cone all the way around. The figure only allows for one sphere to be tangent.
::正如我们从椭圆的证明中了解到的,丹德林球体必须切切到锥形,比如球体在圆圈中环绕锥形,以及飞机,而机体是同一点。 在抛物线下,飞机下方的球体“适合”很好,但飞机上方的球体会“坐在”飞机上,而不会触到锥形。 这个数字只允许一个球体切换。

播放段落

Example 3
::例3

播放段落

Explain why for any positive number $\begin{align*}b\end{align*}$ and $\begin{align*}a\end{align*}$ , there exists a $\begin{align*}c\end{align*}$ such that $\begin{align*}b^2=c^2-a^2\end{align*}$ . Let $\begin{align*}c = \sqrt{a^2+b^2}\end{align*}$ .
::解释为什么对于任何正数b和a, 存在b2=c2-a2. Let c=a2+b2的 c, 为何存在正数b和a。

播放段落

Since $\begin{align*}a^2 + b^2\end{align*}$ is always positive for positive $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ , this number is always defined. Geometrically, let $\begin{align*}c\end{align*}$ be the hypotenuse of a right triangle with side lengths $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ .
::a2+b2 对正数a和b总是正数,因此这个数字总是有定义的。从几何角度来说,c是右三角形的侧长a和b的下限。

播放段落

Review
::回顾

播放段落
1. Who was the first mathematician who conceptualized dandelin spheres? When?
   ::谁是第一位将丹德林球体概念化的数学家?何时?
播放段落
2. What is proved by dandelin spheres?
   ::丹德林球体能证明什么?
播放段落
3. How do you identify the foci of an ellipse using dandelin spheres?
   ::你如何使用dandelin球体来辨别 椭圆的角?
播放段落
4. If two tangents are drawn from a single point to a sphere, what can you say about the line segments formed?
   ::如果两个相切点从一个点抽到一个球体, 你能对形成的线条段说些什么?
播放段落
5. How do the tangents relate to a radius of a sphere?
   ::相切点与球体半径有何关联?
播放段落
6. Describe the focal property of ellipses.
   ::描述省略号的焦点属性 。
播放段落
7. How and when did Germinal Dandelin prove the focal property for parabolas?
   ::Germinal Dandelin如何以及何时证明Parabolas的主要财产?
播放段落
8. What is the line that results from the intersection between the cutting plane and the plane that contains the circle of contact between the sphere and cone?
   ::切割平面与包括球体和锥体接触圈的平面之间的交叉点的界线是什么?
播放段落
9. What is defined by the point where the sphere intersects the cutting plane?
   ::球与切割平面交错点的定义是什么?
播放段落
10. Which construction uses two spheres in a single cone?
    ::哪个建筑使用一个锥体的两个区域?
播放段落
11. Which construction uses one sphere in a single cone?
    ::哪个建筑在单一锥形中使用一个球体?
播放段落
12. Which construction uses two spheres and two cones?
    ::哪些建筑使用两个球体和两个锥形?

播放段落

Identify the parts listed on the diagram as specified below:
::标明图表上所列的下列部分:

播放段落
13. Directrix Line - Small Sphere
    ::直轴线 - 小型环形
播放段落
14. Directrix Line - Large Sphere
    ::直径线 - 大环形
播放段落
15. Focus - Small Sphere
    ::焦点 - 小型球体
播放段落
16. Focus - Large Sphere
    ::焦点 - 大型球体
播放段落
17. Vertex - Small Sphere
    ::顶部 - 小型球体
播放段落
18. Vertex - Large Sphere
    ::顶部 - 大型球体
播放段落
19. Directrix Plane - Small Sphere
    ::直航飞机 -- -- 小型球体
播放段落
20. Directrix Plane - Large Sphere
    ::直航平面 - 大型球体
播放段落
21. Cutting Plane
    ::剪切平板
播放段落
22. What conic section is illustrated here?
    ::这里说明的是哪些二次曲线部分?

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。