节: 标注和函数标注 | 1.3 点名和功能标记

章节大纲

When performing multiple transformations , it is very easy to make a small error. This is especially true when you try to do every step mentally. Point notation is a useful tool for concentrating your efforts on a single point and helps you to avoid making small mistakes.
::当进行多次转换时, 很容易犯一个小错误。当您尝试在精神上做每一步时, 这尤其正确。点符号是一个有用的工具, 用来集中力量于一个点上, 帮助您避免犯小错误。

What would $\begin{align*}f(3x) + 7\end{align*}$ look like in point notation and why is it useful?
::f( 3x)+7 在点符号中长什么样子, 为什么它有用 ?

Using Function Notation and Point Notation
::使用函数符号和点符号

A transformation can be written in and in point notation. Function notation is very common and practical because it allows you to graph any function using the same basic thought process it takes to graph a parabola in vertex form.
::转换可以用点符号写成。函数符号非常常见且实用, 因为它允许您使用相同的基本思维过程来用顶点形状的抛物线绘制任何函数。

Another way to graph a function is to transform each point one at a time. This method works well when a table of $\begin{align*}x, y\end{align*}$ values is available or easily identified from the graph.
::绘制函数的另一种方式是一次转换每个点。当有 x,y 值的表格可用或从图表中很容易识别时,此方法效果良好。

Essentially, it takes each coordinate $\begin{align*}(x, y)\end{align*}$ and assigns a new coordinate based on the transformation.
::基本上,它需要每个坐标(x,y),并根据变换情况指定一个新的坐标。

\begin{aligned} (x, y) ⟶ (new x, new y) \end{aligned}

$\begin{align*}(x, \; y) \longrightarrow (\text{new }x, \; \text{new }y)\end{align*}$
:

x,y)(新x,newy)

This notation is called point notation . The new $\begin{align*}y\end{align*}$ coordinate is straightforward and is directly from what takes place outside $\begin{align*}f(x)\end{align*}$ because $\begin{align*}f(x)\end{align*}$ is just another way to write $\begin{align*}y\end{align*}$ . For example, $\begin{align*}f(x) \rightarrow 2f(x) - 1\end{align*}$ would have a new $\begin{align*}y\end{align*}$ coordinate of $\begin{align*}2y-1\end{align*}$ .
::此符号称为点符号。新的 Y 坐标是直截了当的, 直接来自 f( x) 以外发生的情况, 因为 f( x) 只是写 y 的另一种方式。例如, f( x)% 2f( x) - 1 将有一个 2y-1 的新的 Y 坐标。

The new $\begin{align*}x\end{align*}$ coordinate is trickier. It comes from undoing the operations that affect $\begin{align*}x\end{align*}$ . For example, $\begin{align*}f(x) \rightarrow f(2x -1)\end{align*}$ would have a new $\begin{align*}x\end{align*}$ coordinate of $\begin{align*}\frac{x +1}{2}\end{align*}$ .
::新的 x 坐标更狡猾。它来自撤销影响 x 的操作。例如, f( x)\f( 2x- 1) 将有一个 x+12 的新的 x 坐标。

The function notation and point notation representations of the transformation " Horizontal shift right three units, vertical shift up 4 units" are
::变换的函数符号和点符号表示“三对位移动右下三单位,垂直向上移动4个单位”

$\begin{align*}f(x) \rightarrow f(x-3)+4\end{align*}$
:xx)f(x-3)+4

$\begin{align*}(x,y) \rightarrow (x+3,y+4)\end{align*}$
:x,y)(x+3,y+4)

Notice that the operations with the $\begin{align*}x\end{align*}$ are different.
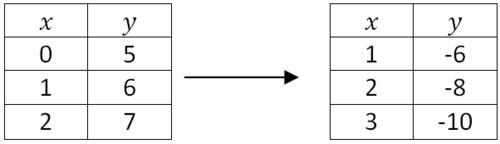
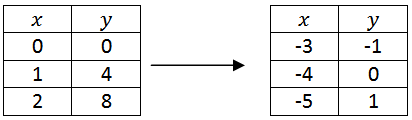
::注意 x 的操作不同。

Apply the transformation above to the following table of points.
::将以上转换应用到下个点表。

\begin{aligned} x \end{aligned}

$\begin{align*}\large{x}\end{align*}$
::x x

\begin{aligned} y \end{aligned}

$\begin{align*}\large{y}\end{align*}$
::y y , y

\begin{aligned} 1 \end{aligned}

$\begin{align*}1\end{align*}$

\begin{aligned} 3 \end{aligned}

$\begin{align*}3\end{align*}$

\begin{aligned} 2 \end{aligned}

$\begin{align*}2\end{align*}$

\begin{aligned} 5 \end{aligned}

$\begin{align*}5\end{align*}$

\begin{aligned} 8 \end{aligned}

$\begin{align*}8\end{align*}$

\begin{aligned} - 11 \end{aligned}

$\begin{align*}-11\end{align*}$

Notice that point notation greatly reduces the mental visualization required to keep all the transformations straight at once.
::注意点记数会大大降低使所有变形保持同步所需的心理直观化

Examples
::实例

Example 1
::例1

Earlier, you were asked what the function $\begin{align*}f(3x) +7\end{align*}$ would be when written in point notation. When written in point notation, it would be written as $\begin{align*}(x, y) \rightarrow \left (\frac{x}{3}, y+7 \right )\end{align*}$ . This is useful because it becomes obvious that the $\begin{align*}x\end{align*}$ values are all divided by three and the $\begin{align*}y\end{align*}$ values all increase by 7.
::早些时候,有人问您在用点符号写入 f( 3x)+7 函数时, F( 3x)+7 会是什么。当用点符号写入时, 它会被写成 (x,y) {( x3,y+7) 。这很有用, 因为很明显, x 值除以 3, y 值都增加了 7 。

Example 2
::例2

Convert the following function in point notation to words and then function notation.
::将以下函数以点符号转换为单词,然后函数符号。

$\begin{align*}(x,y)\rightarrow(3x+1,-y+7)\end{align*}$
:x,y)(3x+1,-y+7)

Horizontal stretch by a factor of 3 and then a horizontal shift right one unit. Vertical reflection over the $\begin{align*}x\end{align*}$ axis and then a vertical shift 7 units up.
::水平伸展为 3 乘以 3, 然后向右水平倾斜一个单位。垂直反射在 x 轴上方, 然后向上垂直移动 7 个单位。

$\begin{align*}f(x)\rightarrow -f \left ( \frac{1}{3}x - \frac{1}{3} \right ) +7\end{align*}$
:xx)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\7\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Example 3
::例3

Convert the following function notation into words and then point notation. Finally, apply the transformation to three example points.
::将以下函数符号转换为单词,然后点符号。最后,将转换应用到三个示例点。

$\begin{align*}f(x) \rightarrow - 2f(x-1) + 4\end{align*}$
:xx)%2f(x-1)+4

Vertical reflection across the $\begin{align*}x\end{align*}$ axis. Vertical stretch by a factor of 2. Vertical shift 4 units. Horizontal shift right one unit.
::垂直反射横跨 x 轴。垂直伸展以 2 的系数为 2 。垂直倾斜 4 单位。水平向右倾斜。

$\begin{align*}(x,y)\rightarrow(x+1,- 2y+4)\end{align*}$
:x,y)(x+1,--2y+4)

Example 4
::例4

Convert the following function notation into point notation and apply it to the included table of points
::将以下函数符号转换为点符号并将其应用到包含的点表

$\begin{align*}f(x) \rightarrow \frac{1}{4} f(-x-3)-1\end{align*}$
:xx)14f(-x-3)-1

\begin{aligned} x \end{aligned}

$\begin{align*}\large{x}\end{align*}$
::x x

\begin{aligned} y \end{aligned}

$\begin{align*}\large{y}\end{align*}$
::y y , y

\begin{aligned} 1 \end{aligned}

$\begin{align*}1\end{align*}$

\begin{aligned} 4 \end{aligned}

$\begin{align*}4\end{align*}$

\begin{aligned} 2 \end{aligned}

$\begin{align*}2\end{align*}$

\begin{aligned} 8 \end{aligned}

$\begin{align*}8\end{align*}$

The $\begin{align*}y\end{align*}$ component can be directly observed. For the $\begin{align*}x\end{align*}$ component you need to undo the argument. $\begin{align*}(x, y) \rightarrow \left ( - x-3,\frac{1}{4} y-1 \right )\end{align*}$
::y 组件可以直接观测。对于 x 组件, 您需要撤消参数。 (x, y) {(- x-3, 14y- 1)

Example 5
::例5

Convert the following point notation to words and to function notation and then apply the transformation to the included table of points.
::将以下点数转换为单词和函数符号,然后对包含的点表应用转换。

$\begin{align*}(x+3,y-1) \rightarrow (2x+6,-y)\end{align*}$
:x+3,y-1)________________________(2x+6,-y)

\begin{aligned} x \end{aligned}

$\begin{align*}\large{x}\end{align*}$
::x x

\begin{aligned} y \end{aligned}

$\begin{align*}\large{y}\end{align*}$
::y y , y

\begin{aligned} 10 \end{aligned}

$\begin{align*}10\end{align*}$

\begin{aligned} 8 \end{aligned}

$\begin{align*}8\end{align*}$

\begin{aligned} 12 \end{aligned}

$\begin{align*}12\end{align*}$

\begin{aligned} 7 \end{aligned}

$\begin{align*}7\end{align*}$

\begin{aligned} 14 \end{aligned}

$\begin{align*}14\end{align*}$

\begin{aligned} 6 \end{aligned}

$\begin{align*}6\end{align*}$

This problem is different because it seems like there is a transformation happening to the original left point. This is an added layer of challenge because the transformation of interest is just the difference between the two points. Notice that the $\begin{align*}x\end{align*}$ coordinate has simply doubled and the $\begin{align*}y\end{align*}$ coordinate has gotten bigger by one and turned negative. This problem can be rewritten as:
::这个问题是不同的, 因为它似乎正在向原始左点转变。这是一个额外的挑战层, 因为利益转变只是两个点之间的差别。请注意, x 坐标只翻了一番, Y 坐标又变大了一个, 反转为负。这个问题可以重写为 :

$\begin{align*}(x,y) \rightarrow (2x,-(y+1) )=(2x,-y-1)\end{align*}$
:x,y)(2x,-(y+1))=(2x,----1)

$\begin{align*}f(x) \rightarrow - f \left ( \frac{x}{2} \right )-1\end{align*}$
:xx)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Remember this!

Function notation shows the transformation of the entire function all at once.
::函数符号显示整个函数的瞬间转换。

Point notation shows the transformation of each coordinate separately.
::点符号显示每个坐标的变换。

For example:
Function notation: $\begin{align*}f(x) \rightarrow f(x-3)+4\end{align*}$
Point notation: $\begin{align*}(x,y) \rightarrow (x+3,y+4)\end{align*}$
::例如: 函数符号: f(x)\\f(x-3)+4 点符号x,y)_(x+3,y+4)

Review
::回顾

Convert the following function notation into words and then point notation. Finally, apply the transformation to three example points.

\begin{aligned} x \end{aligned}

$\begin{align*}\large{x}\end{align*}$
::x x

\begin{aligned} y \end{aligned}

$\begin{align*}\large{y}\end{align*}$
::y y , y

\begin{aligned} 5 \end{aligned}

$\begin{align*}5\end{align*}$

\begin{aligned} 1 \end{aligned}

$\begin{align*}1\end{align*}$

\begin{aligned} 6 \end{aligned}

$\begin{align*}6\end{align*}$

\begin{aligned} 2 \end{aligned}

$\begin{align*}2\end{align*}$

\begin{aligned} 7 \end{aligned}

$\begin{align*}7\end{align*}$

1. $\begin{align*}f(x) \rightarrow -\frac{1}{2} f(x+1)\end{align*}$
::1. f(x) 12f(x+1)

2. $\begin{align*}g(x)\rightarrow 2g(3x)+2\end{align*}$
::2. g(x)_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3. $\begin{align*}h(x) \rightarrow - h(x-4)-3\end{align*}$
::3. h(x)h(x-4)-3

4. $\begin{align*}j(x) \rightarrow 3j(2x-4)+1\end{align*}$
::4. j(x)3j(2x-4)+1

5. $\begin{align*}k(x)\rightarrow -k(x-3)\end{align*}$
::5. k(x)\\\\ k(x- 3)

Convert the following functions in point notation to function notation.
::以点符号转换以下函数为函数符号。

6. $\begin{align*}(x,y) \rightarrow \left ( \frac{1}{2} x+3,y-4 \right )\end{align*}$
::6. (x,y)(12x+3,y-4)

7. $\begin{align*}(x,y) \rightarrow (2x+4,-y+1)\end{align*}$
::7.(x,y)(2x+4,-y+1)

8. $\begin{align*}(x,y) \rightarrow (4x,3y-5)\end{align*}$
::8. (x,y)(4x,3y-5)

9. $\begin{align*}(2x,y) \rightarrow (4x, - y+1)\end{align*}$
::9. (2x,y)(4x,-y+1)

10. $\begin{align*}(x+1,y-2) \rightarrow (3x+3, -y+3)\end{align*}$
::10. (x+1,y-2)(3x+3,-y+3)

Convert the following functions in function notation to point notation.
::将函数符号中的下列函数转换为点符号。

11. $\begin{align*}f(x) \rightarrow 3f(x-2)+1\end{align*}$
::11. f(x)3f(x-2)+1

12. $\begin{align*}g(x) \rightarrow -4g(x-1)+3\end{align*}$
::12. g(x)4g(x-1)+3

13. $\begin{align*}h(x) \rightarrow \frac{1}{2} h(2x+2)-5\end{align*}$
::13. h(x)12h(2x+2)-5

14. $\begin{align*}j(x) \rightarrow 5j \left ( \frac{1}{2} x-2 \right )-1\end{align*}$
::14. j(x)5j(12x-2)-1

15. $\begin{align*}k(x) \rightarrow \frac{1}{4} k(2x-4)\end{align*}$
::15. k( x) }14k( 2x- 4)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Using Function Notation and Point Notation ::使用函数符号和点符号

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Using Function Notation and Point Notation
::使用函数符号和点符号

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)