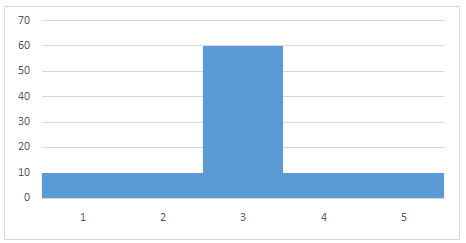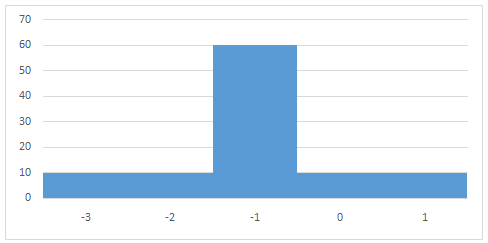节: 变换随机变量I | 7.9 变换随机变量一

章节大纲

Suppose you are running a lemonade stand, and you know that you have a mean of 15 customers per hour, with a standard deviation of 5 customers. If you know that it costs you 30 cents per glass in materials, and that you could hire your little sister to work the stand for you for $4.50 per hour, how could you calculate the mean and standard deviation of the cost per hour of having your sister run the stand?
::假设你正在经营一个柠檬水摊位,你知道你每小时平均有15个顾客,标准偏差为5个顾客。如果你知道每杯每杯材料花费你30美分,而且你可以雇你妹妹为你工作,每小时4.50美元,你怎么能计算你妹妹主持摊位每小时费用的平均和标准偏差?

At the end of this lesson we will know one part of the answer. We will learn the other part in the next lesson, so stay tuned!
::在这个教训结束时,我们将知道答案的一部分。我们将在下一个教训中学到另一部分,所以请保持关注!

Transforming Random Variables
::变换随机变量

Sometimes it is useful to be able to calculate how the mean and standard deviation of a random variable is affected by adding or subtracting a constant to each outcome. For example, suppose you were able to calculate the mean labor and materials cost per hour at your pizza store, based on the probabilities of there being different numbers of orders per hour. If you wanted to learn how it would affect your bottom line to hire an employee, you might want to compare the increased income and expense of adding 8 orders per hour. Since you could use a random variable to represent number of customers per hour, you would need to add 8 to every possible outcome of the random variable, which could take quite a while. Rather than having to then recalculate the mean, variance , and standard deviation using all new data , it would be great to know how adding a constant (like 8, for instance) affects the mean and variance of a random variable directly.
::有时,如果能够计算随机变量的平均值和标准偏差是如何通过在每个结果中增加或减去一个常数而受到影响的。例如,假设你能够根据每小时不同订单的概率来计算比萨店每小时的平均劳动和材料成本。如果你想了解每小时增加8个订单对底线的影响,那么你可能想要比较每小时增加8个订单的增额和费用。由于您可以使用随机变量来代表每小时的客户数量,因此您需要在随机变量的每一种结果中增加8个,这可能需要相当长的时间。与其再用所有新数据重新计算平均值、差异和标准偏差,了解增加一个常数(例如8个)如何直接影响随机变量的平均值和差异,那将是非常有益的。

Perhaps the most important realization here is that adding or subtracting a constant from the outcomes of a random variable changes all of the outcomes by the same amount. Look at the distribution graph here, it represents the probability distribution of random variable $\begin{aligned} X \end{aligned}$ :
::也许最重要的认识是,从随机变数变化的结果中增加或减去一个常数,所有结果以相同数额计算。看此分布图,它代表随机变数X的概率分布:

This distribution has a mean of 3 and a standard deviation of 1. In other words:
::这种分布的平均值为3,标准差为1.,换句话说:

\begin{aligned} μ_{X} & = 3 \\ σ_{X} & = 1 \end{aligned}

::μX=3-13-X=1

If all of the values on the chart were increased or decreased by the same amount, then the position of the mean would move left or right across the graph, but the relative position of each bar would not change.
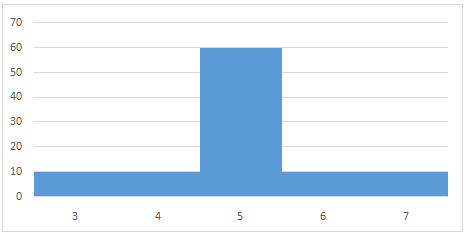
::如果图表上的所有值都增加或减少相同数额,则平均值的位置会向左或向右移动,但每个栏的相对位置不会改变。

To see the effect of adding a constant to the outcomes, let’s look at the distribution of $\begin{aligned} X + 2 \end{aligned}$ :
::让我们看看X+2的分布。

Now the distribution has a mean of 5, but the standard deviation is still 1:
::现在分布的平均值是5, 但标准偏差仍然是 1 :

\begin{aligned} μ_{X + 2} & = 5 \\ σ_{X + 2} & = 1 \end{aligned}

::μX+2=5XX+2=1

What happens if we subtract a value? Let’s take a look at $\begin{aligned} X - 4 \end{aligned}$ :
::如果我们减去一个值会怎么样?让我们看看X-4:

Now the mean has gone down by four, to -1, but the standard deviation is still unchanged:
::现在平均值下降了四倍,降至-1,但标准偏差仍然未变:

\begin{aligned} μ_{X - 4} & = - 1 \\ σ_{X - 4} & = 1 \end{aligned}

::X-4134=1

Solving for Unknown Values
::解决未知值

1. If $\begin{aligned} μ_{X} = 5 \end{aligned}$ , and $\begin{aligned} σ_{X} = 2.4 \end{aligned}$ , what is $\begin{aligned} μ_{X + 3.5} \end{aligned}$ and $\begin{aligned} σ_{X + 3.5} \end{aligned}$ ?
::1. 如果 μX=5, 和 X=2.4, mX+3.5 和 X+3.5 是什么?

When adding or subtracting a constant to/from a random variable, the mean is changed directly by the constant, but the standard deviation remains unchanged.
::当向随机变量增减常数时,平均值会直接由常数改变,但标准偏差保持不变。

In this example, $\begin{aligned} μ_{X} = 5 \end{aligned}$ , so $\begin{aligned} μ_{X + 3.5} = 5 + 3.5 = 8.5 \end{aligned}$
::在此示例中, μX=5, 所以 μX+3.5=5+3.5=8.5

Since we are simply adding a constant, 3.5, to $\begin{aligned} X \end{aligned}$ , the standard deviation remains unchanged, so $\begin{aligned} σ_{X + 3.5} = 2.4 \end{aligned}$ .
::由于我们仅仅是在X中加上一个常数3.5,因此标准差保持不变,因此为 +X+3.5=2.4。

2. If $\begin{aligned} μ_{Y} = 13.7 \end{aligned}$ , and $\begin{aligned} σ_{Y} = 6.7 \end{aligned}$ , what is $\begin{aligned} μ_{Y - 1.4} \end{aligned}$ and $\begin{aligned} σ_{Y - 1.4} \end{aligned}$ ?
::2. 如果μY=13.7, 和 .12/Y=6.7, 微Y-1.4和 □Y-1.4是什么?

Similar to the last example, here we are subtracting a constant from a random variable, so we expect the mean to be reduced, and the standard deviation to remain unchanged.
::与最后一个例子相似,我们在这里从随机变量中减去一个常数,因此我们期望减少平均值,标准偏差保持不变。

$\begin{aligned} μ_{Y} = 13.7 \end{aligned}$ , so $\begin{aligned} μ_{Y - 1.4} = 13.7 - 1.4 = 12.3 \end{aligned}$
::微Y=13.7, 所以微Y-1.4 = 13.7 - 1.4= 12.3

$\begin{aligned} σ_{Y} = 6.7 \end{aligned}$ , and standard deviation does not change when adding or subtracting a constant from a random variable, so $\begin{aligned} σ_{Y - 1.4} = 6.7 \end{aligned}$ also.
::{Y=6.7}在从随机变量中增加或减去一个常数时,标准差不会改变,因此 {Y=1.4=6.7。

Real-World Application: Dog Walking

::真实世界应用程序:狗行走

Sayber walks dogs for money on weekends, and he has compiled the following probability distribution of the number of dogs he is likely to walk each day.
::Sayber在周末为钱而走狗,他汇编了他每天可能走路的狗数的概率分布如下。

# clients ::* 客户	13	17	22	27	32
probability ::概率概率概率	.10	.25	.30	.25	.10

a. If he earns $7.50 per dog, how much should he expect to earn each day, on average ?
::a. 如果他每只狗挣7.50美元,他平均每天预期挣多少?

Start by setting a random variable, we’ll use $\begin{aligned} D \end{aligned}$ , to represent the number of dogs he walks. Then we can calculate the mean of $\begin{aligned} D \end{aligned}$ , using the formula: $\begin{aligned} μ_{x} = \sum [x \times P (x)] \end{aligned}$ .
::首先设定一个随机变量, 我们将使用 D 来代表他走路的狗数量。然后我们可以使用公式 : μx[xxxP(x)] 来计算 D 的平均值。

\begin{aligned} μ_{D} & = (13 \times .1) + (17 \times .25) + (22 \times .3) + (27 \times .25) + (32 \times .10) = 22.1 \\ μ_{D} & = 22.1 \end{aligned}

::μD=(13x.1)+(17x.25)+(22x.3)+(27x.25)+(32x.10)=22.1μD=22.1

That means Sayber could expect to earn $\begin{aligned} 22.1 \times $ 7.50 = $ 165.75 \end{aligned}$ each day, on average.
::这意味着Sayber平均每天平均可挣22.1美元×7.50美元=165.75美元。

b. How would it affect his mean income if he were to get 5 more dogs each day?
::b. 如果他每天多养5只狗,他的平均收入会受到什么影响?

If the mean of the number of dogs was 22.1 to start with, and Sayber were to add 5 dogs to each of the values he started with on his probability distribution, that would be the same as calculating $\begin{aligned} μ_{D + 5} \end{aligned}$ , which we now know would result in an average of $\begin{aligned} 22.1 + 5 = 27.1 \end{aligned}$ . His income then would be $\begin{aligned} 27.1 \times $ 7.5 = $ 203.25 \end{aligned}$ .
::如果狗的平均数从22.1开始,Sayber的概率分布每开始的数值中增加5只狗,这与计算μD+5的数值相同,我们现在知道这个数值将平均产生22.1+5=27.1。那么他的收入将是27.1×7.5美元=203.25美元。

Earlier Problem Revisited

::重审先前的问题

By using the skills we learned in this lesson, you could convert the cost of running the stand yourself to hiring your sister, by adding $4.50 to the average hourly cost. Unfortunately, we can’t actually solve the problem yet, because we haven’t learned how to deal with the $0.30 per glass in materials cost, that is the next lesson!
::利用我们在这个教训中学到的技能,你可以将自己经营摊位的成本转换为雇用你妹妹,在每小时平均成本中增加4.50美元。不幸的是,我们实际上还不能解决问题,因为我们还没有学会如何处理每杯0.30美元的材料成本,这是下一个教训!

Examples
::实例

Example 1
::例1

If $\begin{aligned} μ_{C} = 12 \end{aligned}$ and $\begin{aligned} σ_{C} = .7 \end{aligned}$ , what is $\begin{aligned} μ_{C + 6.4} \end{aligned}$ and $\begin{aligned} σ_{C + 6.4} \end{aligned}$ ?
::如果μC=12 和 +C=7, 则mC+6.4和 +C+6.4是什么?

Since $\begin{aligned} μ_{C} = 12 \end{aligned}$ , and $\begin{aligned} σ_{C} = .7 \end{aligned}$ , and adding a constant to a random variable affects the mean directly, but does not change the variance or standard deviation, $\begin{aligned} μ_{C + 6.4} = 12 + 6.4 = 18.4 \end{aligned}$ and $\begin{aligned} σ_{C + 6.4} = .7 \end{aligned}$ .
::由于 μC=12, 和 +C=7, 并在随机变量中增加一个常数直接影响到平均值,但不会改变差异或标准差,因此, μC+6.4=12+6.4=18.4和 aspC+6.4=7。

Example 2
::例2

If $\begin{aligned} μ_{Y} = 113 \end{aligned}$ , and $\begin{aligned} σ_{Y} = 12.22 \end{aligned}$ , what is $\begin{aligned} μ_{Y - 17.4} \end{aligned}$ and $\begin{aligned} σ_{Y - 17.4} \end{aligned}$ ?
::如果微克Y=113, 和Y=12.22, 微Y-17.4 和 Y-17.4 是什么?

Since $\begin{aligned} μ_{Y} = 113 \end{aligned}$ , and $\begin{aligned} σ_{Y} = 12.22 \end{aligned}$ , that means $\begin{aligned} μ_{Y - 17.4} = 113 - 17.4 = 95.6 \end{aligned}$ , and $\begin{aligned} σ_{Y - 17.4} = 12.22 \end{aligned}$ (unchanged).
::由于微Y=113, 和Y=12.22, 这意味着微Y-17.4=113-17.4=95.6, 和Y-17.4=12.22(未改变)。

Example 3
::例3

If a production line has an error tolerance of 4 parts per ten thousand within 1 standard deviation of the mean, and currently has a mean error rate of .0002, with a standard deviation of .00005, would it be acceptable to increase the speed of production by 12% if it resulted in an increased error rate of .00013?
::如果生产线在平均值的1个标准差内有每万分之4的误差容忍度,而且目前平均误差率为0.002,标准差为0.005,那么如果生产线的误差率上升为0.0013,将生产速度提高12%是可以接受的吗?

If the line must maintain an error rate of $\begin{aligned} < .0004 \end{aligned}$ within one standard deviation of the mean, and currently ranges from $\begin{aligned} - 1 S D = .0002 - .00005 = .00015 \end{aligned}$ to $\begin{aligned} + 1 S D = .0002 + .00005 = .00025 \end{aligned}$ . There are two different way to look at this:
::如果线条必须在平均值的一个标准差内保持 <.0004 误差率,且目前介于-1SD=.0002-.0005=.00015至+1SD=.0002+.0005=.00025之间。

If the current error rate has a maximum of .00025, that means there is a “safety net” of $\begin{aligned} .0004 - .00025 = .00015 \end{aligned}$ . Since $\begin{aligned} .00013 < .00015 \end{aligned}$ , the increased error is acceptable, just barely.
::如果当前错误率最高为 .00025, 则意味着“ 安全网”为.0004-.00025=.00015。由于 .00013 <.00015, 增加的错误是可以接受的, 只是勉强可以接受。

Alternately, we can recall that adding a constant to a random variable affects the mean directly, but does not affect the standard deviation. So adding 0.00013 to the error rate would increase the mean to $\begin{aligned} .00025 + .00013 = .00038 \end{aligned}$ , which, again, is just barely within tolerance.
::作为替代,我们可以回顾,在随机变量中添加一个常数直接影响到平均值,但不影响标准偏差。因此,在误差率中添加 0.00013 将会将平均值提高到 .00025+.00013=.00038, 这同样也几乎无法容忍。

Review
::回顾

For questions 1-10, add or subtract the given constant from the random variable:
::对于问题1-10, 从随机变量中加上或减去给定的常数:

If $\begin{aligned} μ_{X} = .07 \end{aligned}$ , and $\begin{aligned} σ_{X} = .002 \end{aligned}$ , what is $\begin{aligned} μ_{X + .02} \end{aligned}$ and $\begin{aligned} σ_{X + .02} \end{aligned}$ ?
::如果 μX=.07, 和 X=.002, mX+.02 和 X+.02 是什么?

If $\begin{aligned} μ_{C} = 144 \end{aligned}$ , and $\begin{aligned} σ_{C} = 17 \end{aligned}$ , what is $\begin{aligned} μ_{C + 13.6} \end{aligned}$ and $\begin{aligned} σ_{C + 13.6} \end{aligned}$ ?
::如果 μC=144, 和 □C=17, mC+13.6 和 □C+13.6 是什么?

If $\begin{aligned} μ_{Y} = 22 \end{aligned}$ , and $\begin{aligned} σ_{Y} = 1.8 \end{aligned}$ , what is $\begin{aligned} μ_{Y - 3.49} \end{aligned}$ and $\begin{aligned} σ_{Y - 3.49} \end{aligned}$ ?
::如果μY=22, 和 .12/Y=1.8, mY- 3.49 和 □Y-3.49 是什么?

If $\begin{aligned} μ_{Z} = 68.33 \end{aligned}$ , and $\begin{aligned} σ_{Z} = 4.87 \end{aligned}$ , what is the $\begin{aligned} μ \end{aligned}$ and $\begin{aligned} σ \end{aligned}$ of $\begin{aligned} Z + 4.25 \end{aligned}$ ?
::若是68.33和4.87, 4.25的微米和是多少?

If $\begin{aligned} μ_{X} = 2.071 \end{aligned}$ , and $\begin{aligned} σ_{X} = .807 \end{aligned}$ , what is the $\begin{aligned} μ \end{aligned}$ and $\begin{aligned} σ \end{aligned}$ of $\begin{aligned} X - 1.035 \end{aligned}$ ?
::如果 μX= 2.071 和 X=.807, X-1.035 的微克和是什么 ?

If $\begin{aligned} μ_{A} = \frac{3}{5} \end{aligned}$ , and $\begin{aligned} σ_{A} = \frac{1}{5} \end{aligned}$ , what is the $\begin{aligned} μ \end{aligned}$ and $\begin{aligned} σ \end{aligned}$ of $\begin{aligned} A + \frac{3}{10} \end{aligned}$ ?
::如果 μA=35, 和 A=15, A+310 的微克和是什么?

If $\begin{aligned} μ_{B} = 17.031 \end{aligned}$ , and $\begin{aligned} σ_{B} = 2.101 \end{aligned}$ , what is the $\begin{aligned} μ \end{aligned}$ and $\begin{aligned} σ \end{aligned}$ of $\begin{aligned} B - .035 \end{aligned}$ ?
::如果μB=17.031,和 B=2.101,B-.035的微克和是什么?

If $\begin{aligned} μ_{A} = \frac{2}{7} \end{aligned}$ , and $\begin{aligned} σ_{A} = \frac{1}{7} \end{aligned}$ , what is the $\begin{aligned} μ \end{aligned}$ and $\begin{aligned} σ \end{aligned}$ of $\begin{aligned} A - \frac{3}{14} \end{aligned}$ ?
::如果 μA=27, 和 A=17, A-314 的微克和是什么 ?

If $\begin{aligned} μ_{Y} = 13.1 \end{aligned}$ , and $\begin{aligned} σ_{Y} = 3.01 \end{aligned}$ , what is the $\begin{aligned} μ \end{aligned}$ and $\begin{aligned} σ \end{aligned}$ of $\begin{aligned} Y + .27 \end{aligned}$ ?
::如果微克Y=13.1,和 .12/Y=3.01,Y+27的微克和是什么?

If $\begin{aligned} + 1 S D \end{aligned}$ of $\begin{aligned} μ_{X} = 4.25 \end{aligned}$ and $\begin{aligned} - 1 S D \end{aligned}$ of $\begin{aligned} μ_{X} = 3.75 \end{aligned}$ , what is $\begin{aligned} μ_{X + 2} \end{aligned}$ and $\begin{aligned} σ_{X + 2} \end{aligned}$ ?
::如果+1SDofμX=4.25 和-1-SDofμX=3.75,什么是μX+2 和 X+2?

If $\begin{aligned} + 1 S D \end{aligned}$ of $\begin{aligned} μ_{X} = 11.25 \end{aligned}$ and $\begin{aligned} - 1 S D \end{aligned}$ of $\begin{aligned} μ_{X} = 9.75 \end{aligned}$ , what is $\begin{aligned} μ_{X - 1.25} \end{aligned}$ and $\begin{aligned} σ_{X - 1.25} \end{aligned}$ ?
::如果+1SDofμX=11.25和-1SDofμX=9.75,什么是μX-1.25和X-1.25?

If $\begin{aligned} + 2 S D \end{aligned}$ of $\begin{aligned} μ_{X} = 25 \end{aligned}$ and $\begin{aligned} - 2 S D \end{aligned}$ of $\begin{aligned} μ_{X} = 5 \end{aligned}$ , what is $\begin{aligned} μ_{X - 4} \end{aligned}$ and $\begin{aligned} σ_{X - 4} \end{aligned}$ ?
::如果+2SDofμX=25和-2SDofμX=5,那么μX-4和X-4是什么?

If $\begin{aligned} - 2 S D \end{aligned}$ of $\begin{aligned} μ_{Z} = 9 \end{aligned}$ and $\begin{aligned} + 2 S D \end{aligned}$ of $\begin{aligned} μ_{Z} = 15 \end{aligned}$ , what is $\begin{aligned} μ_{Z - .75} \end{aligned}$ and $\begin{aligned} σ_{Z - .75} \end{aligned}$ ?
::如果 -2SDof%9 和+2SDof%15, 是什么是75 和75?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Transforming Random Variables ::变换随机变量

Solving for Unknown Values ::解决未知值

Real-World Application: Dog Walking ::真实世界应用程序:狗行走

Earlier Problem Revisited ::重审先前的问题

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)