节: 多元扩张和帕斯卡尔三角 | 2.3 多元扩张和帕斯卡尔三角

章节大纲

The expression $\begin{aligned} (2 x + 3)^{5} \end{aligned}$ would take a while to multiply out. Is there a pattern you can use?
::表达式( 2x+3) 5 需要一段时间才能乘出。您可以使用模式吗 ?

Expansion with Pascal's Triangle
::扩展与帕斯卡尔三角

Expanding a Binomial
::正在扩大二进制

Pascal was a French mathematician in the $\begin{aligned} 17^{t h} \end{aligned}$ century, but the triangle now named Pascal’s Triangle was studied long before Pascal used it. The pattern was used around the $\begin{aligned} 10^{t h} \end{aligned}$ century in Persia, India and China as well as many other places.
::帕斯卡尔是17世纪的法国数学家,但现在称为帕斯卡尔三角的三角形早在帕斯卡尔使用之前就已经进行了研究。 10世纪前后,波斯、印度和中国以及其他许多地方都采用了这个模式。

The primary purpose for using this triangle is to introduce how to expand binomials.
::使用此三角形的主要目的是介绍如何扩大二元论。

\begin{aligned} (x + y)^{0} & = 1 \\ (x + y)^{1} & = x + y \\ (x + y)^{2} & = x^{2} + 2 x y + y^{2} \\ (x + y)^{3} & = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} \end{aligned}

x+y) 0=1(x+y) 1=x+y(x+y) 2=x2+2xy(x+y)3=x3+3x2y+3x2+y3)

Notice that the coefficients for the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ terms on the right hand side line up exactly with the numbers from Pascal’s triangle. This means that given $\begin{aligned} (x + y)^{n} \end{aligned}$ for any power $\begin{aligned} n \end{aligned}$ you can write out the expansion using the coefficients from the triangle. Note that to write the coefficients for any power $\begin{aligned} n \end{aligned}$ , you need to look at row $\begin{aligned} n + 1 \end{aligned}$ to find the coefficients.
::请注意右手边的 x 和 y 条件的系数与 Pascal 三角形的数值完全一致。这意味着给 n 任何功率的给定 (x+y) n 您可以使用三角形的系数来写出扩展。请注意, 写任何功率 n 的系数时, 您需要查看 n+1 行来找到系数。

If you were asked to expand $\begin{aligned} (3 x - 2)^{4} \end{aligned}$ using Pascal's Triangle, you would look at the 5th row to find the coefficients. The coefficients will be 1, 4, 6, 4, 1; however, since there are already coefficients with the $\begin{aligned} x \end{aligned}$ and the constant term you must be particularly careful.
::如果您被要求使用帕斯卡三角形扩大( 3x-2) 4, 您将查看第五行寻找系数。系数将为 1, 4, 6, 4, 1; 但是, 由于 x 和常数已经存在系数, 您必须特别小心。

$\begin{aligned} 1 \cdot (3 x)^{4} + 4 \cdot (3 x)^{3} \cdot (- 2) + 6 \cdot (3 x)^{2} \cdot (- 2)^{2} + 4 \cdot (3 x) \cdot (- 2)^{3} + 1 \cdot (- 2)^{4} \end{aligned}$
::1(3x)4+4(3x)3(2)+6(3x)2(2)2+4(3x)__(2)3+1(2)4

Then it is only a matter of multiplying out and keeping track of negative signs.
::而这仅仅是一个乘数的增加和追踪消极迹象的问题。

$\begin{aligned} 81 x^{4} - 216 x^{3} + 216 x^{2} - 96 x + 16 \end{aligned}$
::81x4-216x3+216x2-96x+16

When you study how to count with combinations then you will be able to calculate the value of any coefficient without writing out the whole triangle.
::当您研究如何用组合来计算时, 就可以计算任何系数的值, 而不写出整个三角形。

Patterns and Pascal's Triangle
::模式和帕斯卡尔三角

There are many patterns in the triangle. Here are just a few.
::三角形中有许多图案。这里只有几个图案。

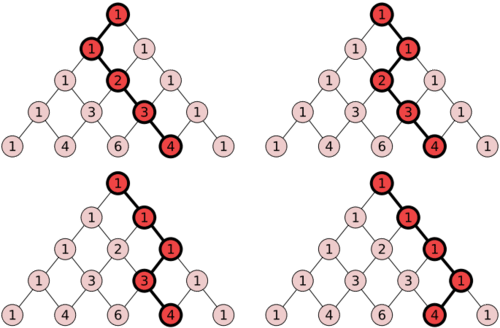
Notice the way each number is created by summing the two numbers above on the left and right hand side.
::注意每个数字是如何通过在左手侧和右手侧对上面两个数字进行打乱而生成的。

As you go further down the triangle the values in a row approach a bell curve . This is closely related to the normal distribution in statistics.
::当您沿着三角形走下去时,一行中的值接近一个钟曲线。这与统计的正常分布密切相关。

For any row that has a second term that is prime, all the numbers besides 1 in that row are divisible by that prime number.
::对于任何第二任期为质数的行,该行中除1之外的所有数字都可被该质数分辨。

Real Life Use : In the game Plinko where an object is dropped through a triangular array of pegs, the probability (which corresponds proportionally to the values in the triangle) of landing towards the center is greater than landing towards the edge. This is because every number in the triangle indicates the number of ways a falling object can get to that space through the preceding numbers.
::真实生命使用 : 在游戏 Plinko 中, 一个对象通过三角形钉形阵列投下, 向中心着陆的概率( 与三角形中的数值成正比) 大于向边缘着陆的概率。这是因为三角形中的每个数字都显示一个坠落对象通过前面数字进入该空间的方式的数量。

Examples
::实例

Example 1
::例1

Earlier, you were asked to multiply out $\begin{aligned} (2 x + 3)^{5} \end{aligned}$ . Pascal’s triangle allows you to identify that the coefficients of $\begin{aligned} (2 x + 3)^{5} \end{aligned}$ will be 1, 5, 10, 10, 5, 1. By carefully substituting, the expansion will be:
::早些时候,你被要求乘以(2x+3)5. 帕斯卡尔的三角形,使你能够确定2x+35的系数为1、5、10、10、5、1。

\begin{aligned} 1 \cdot (2 x)^{5} + 5 \cdot (2 x)^{4} \cdot 3 + 10 \cdot (2 x)^{3} \cdot 3^{2} + 10 \cdot (2 x^{2}) \cdot 3^{3} + 5 (2 x)^{1} \cdot 3^{4} + 3^{5} \end{aligned}

::================================================================================================================================================

Simplifying is a matter of arithmetic, but most of the work is done thanks to the patterns of Pascal’s Triangle.
::简化是一个算术问题, 但大部分工作都是由帕斯卡尔三角形模式决定的。

Example 2
::例2

Factor the following polynomial by recognizing the coefficients.
::承认系数,以下列多数值乘以系数。

$\begin{aligned} x^{4} + 4 x^{3} + 6 x^{2} + 4 x + 1 \end{aligned}$
::x4+4x3+6x2+4x1+1

The coefficients are 1, 4, 6, 4, and 1 and those coefficients are on the 5th row. The first row of Pascal's Triangle shows the coefficients for the 0th power so the 5th row shows the coefficients for the 4th power. Thus, the factored form is:
::系数为 1 、 4 、 6 、 4 和 1 , 这些系数在第五行。 Pascal 三角的第一行显示了第 0 种功率的系数, 因此第五行显示了第 4 种功率的系数。因此, 系数的形式是 :

$\begin{aligned} (x + 1)^{4} \end{aligned}$
:x+1)4

Example 3
::例3

Factor the following polynomial by recognizing the coefficients.
::承认系数,以下列多数值乘以系数。

$\begin{aligned} 8 x^{3} - 12 x^{2} + 6 x - 1 \end{aligned}$
::8x3- 12x2+6x- 1

Since the first coefficient is not 1, you need to take the appropriate root of the first term of the expression to find the first term of the binomial. In this case, the first term of the binomial must be $\begin{aligned} 2 x \end{aligned}$ . Also, the last term must be -1 and the power must be 3. Now all that remains is to check.
::由于第一个系数不是1, 您需要从第一个表达的首个任期中找到第一个二进制任期的适当根基。在此情况下, 二进制的第一个任期必须是 2x 。另外, 最后一个任期必须是 - 1 , 权力必须是 3 。现在剩下的只能检查了。

$\begin{aligned} (2 x - 1)^{3} = (2 x)^{3} + 3 (2 x)^{2} \cdot (- 1) + 3 (2 x)^{1} (- 1)^{2} + (- 1)^{3} = 8 x^{3} - 12 x^{2} + 6 x - 1 \end{aligned}$
:2x-1)3=(2x)3+3(2x)2(-1)+3(2x)1(-1)2+(-1)3+(-1)3=8x3-12x2+6x-1)

Example 4
::例4

Expand the following binomial: $\begin{aligned} {(\frac{1}{2} x - 3)}^{5} \end{aligned}$
::展开以下二进制 : (12x-3) 5

You know that the coefficients will be 1, 5, 10, 10, 5, 1.
::你知道系数是 1,5,10,10,5,1

\begin{aligned} 1 {(\frac{1}{2} x)}^{5} + 5 {(\frac{1}{2} x)}^{4} (- 3) + 10 {(\frac{1}{2} x)}^{3} (- 3)^{2} + 10 {(\frac{1}{2} x)}^{2} (- 3)^{3} + 5 (\frac{1}{2} x) (- 3)^{4} + 1 \cdot (- 3)^{5} \end{aligned}

::1(12x)5+5(12x)4(-3)+10(12x)3(-3)2+10(12x)2(-3)3+5(12x)(-3)4+1(3)5

\begin{aligned} = \frac{x^{5}}{32} - \frac{15 x^{4}}{16} + \frac{90 x^{3}}{8} - \frac{270 x^{2}}{4} + \frac{405 x}{2} - 243 \end{aligned}

::=x532-15x416+90x38-270x24+405x2-2-443

Remember to simplify fractions.
::记住要简化分数。

\begin{aligned} = \frac{x^{5}}{32} - \frac{15 x^{4}}{16} + \frac{45 x^{3}}{4} - \frac{135 x^{2}}{2} + \frac{405 x}{2} - 243 \end{aligned}

::=x532-15x416+45x34-135x22+405x2-243

Example 5
::例5

Expand the following trinomial: $\begin{aligned} (x + y + z)^{4} \end{aligned}$
::展开以下三角x+y+z)4

Unfortunately, Pascal's triangle does not apply to trinomials. Instead of thinking of a two dimensional triangle, you would ned to calculate a three dimensional pyramid which is called Pascal's Pyramid. The sum of all five terms below is your answer.
::不幸的是, Pascal 的三角形不适用于三角形。您不考虑二维三角形, 而是要计算一个三维金字塔, 叫做 Pascal 的金字塔。下面所有五个词的总和就是你的答案。

\begin{aligned} 1 x^{4} + 4 x^{3} z + 6 x^{2} z^{2} + 4 x z^{3} + 1 z^{4} \\ 4 x^{3} y + 12 x^{2} y z + 12 x y z^{2} + 4 y z^{3} \\ 6 x^{2} y^{2} + 12 x y^{2} z + 6 y^{2} z^{2} \\ 4 x y^{3} + 4 y^{3} z \\ 1 y^{4} \end{aligned}

Notice how many patterns exist in the coefficients of this layer of the pyramid.
::1x4+4x3z+6x2z2+4x3+1z44x3y+12x2yz+12xyz2+4z36x2y2+12xy2z+6y2z+6y2z24x3+4y3+4y3z3z1y4 注意金字塔这一层的系数存在多少模式。

Summary

Pascal's Triangle is a pattern used to show how to expand binomials.
::Pascal的三角形是一个模式,用来显示如何扩大二进制。

To expand a binomial using Pascal's Triangle, find the appropriate row for the coefficients and multiply them with the terms, keeping track of negative signs.
::为了利用帕斯卡尔三角扩大二进制, 找到合适的系数行, 并用条件乘以它们, 跟踪负面迹象。

Review
::回顾

Factor the following polynomials by recognizing the coefficients.
::承认系数,以下列多数值乘以系数。

1. $\begin{aligned} x^{2} + 2 x y + y^{2} \end{aligned}$
::1. x2+2xy+y2

2. $\begin{aligned} x^{3} + 3 x^{2} + 3 x + 1 \end{aligned}$
::2. x3+3x2+3x1

3. $\begin{aligned} x^{5} + 5 x^{4} + 10 x^{3} + 10 x^{2} + 5 x + 1 \end{aligned}$
::3. x5+5x4+10x3+10x2+5x1

4. $\begin{aligned} 27 x^{3} - 27 x^{2} + 9 x - 1 \end{aligned}$
::4. 27x3-27x2+9x-1

5. $\begin{aligned} x^{3} + 12 x^{2} + 48 x + 64 \end{aligned}$
::5. x3+12x2+48x+64

Expand the following binomials using Pascal’s Triangle.
::使用帕斯卡尔三角展开以下二进制。

6. $\begin{aligned} (2 x - 3)^{3} \end{aligned}$
::6. (2x-3)3

7. $\begin{aligned} (3 x + 4)^{4} \end{aligned}$
::7. (3x+4)4

8. $\begin{aligned} (x - y)^{7} \end{aligned}$
::8.(x-y)7

9. $\begin{aligned} (a + b)^{10} \end{aligned}$
::9. (a+b)10

10. $\begin{aligned} (2 x + 5)^{5} \end{aligned}$
::10.(2x+5)5

11. $\begin{aligned} (4 x - 1)^{4} \end{aligned}$
::11. (4x-1)4

12. $\begin{aligned} (5 x + 2)^{3} \end{aligned}$
::12. (5x+2)3

13. $\begin{aligned} (x + y)^{6} \end{aligned}$
::13. (x+y)6

14. $\begin{aligned} (3 x + 2 y)^{3} \end{aligned}$
::14. (3x+2y)3

15. $\begin{aligned} (5 x - 2 y)^{4} \end{aligned}$
::15. (5x-2y)4

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Expansion with Pascal's Triangle ::扩展与帕斯卡尔三角

Expanding a Binomial ::正在扩大二进制

Patterns and Pascal's Triangle ::模式和帕斯卡尔三角

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)