Section: 解决合理等式 | 2.6 理衡等同

Section outline

The techniques for are extensions of techniques you already know. Recall that when there are fractions in an equation you can multiply through by the denominator to clear the fraction . The same technique helps turn rational expressions into that you already know how to solve. When you multiply by a constant there is no problem, but when you multiply through by a value that varies and could possibly be zero interesting things happen.
::技术是您已经知道的技术的扩展。回顾当公式中存在分数时,您可以通过分母乘以分母来清除分数。同样的技术有助于将理性表达方式转化为您已经知道如何解答的表达方式。当您乘以一个常数时,没有问题,但当您乘以一个变化而可能有零有趣现象的值时,就不会出现问题。

Since every equation is trivially true when both sides are multiplied by zero, how do you account for this when solving rational equations?
::因为当两边乘以零时,每一方程都是微不足道的,所以在解决理性方程时,你如何解释这一点?

Finding Solutions to Rational Equations
::找到合理等式的解决方案

The first step in solving rational equations is to transform the equation into a polynomial equation. This is accomplished by clearing the fraction which means multiplying the entire equation by the common denominator of all the rational expressions. Then you should solve using what you already know. The last thing to check once you have the solutions is that they do not make the denominators of any part of the equation equal to zero when substituted back into the original equation. If so, that solution is called extraneous and is a “fake” solution that was introduced when both sides of the equation were multiplied by a number that happened to be zero.
::解决理性方程式的第一步是将方程式转换成多元方程式。这是通过清除分数来实现的。分数意味着将整个方程式乘以所有理性表达方式的共同分母。然后您应该使用您已经知道的解答。一旦找到解决方案, 最后要检查的是, 当将方程式的任何部分替换为原方程式时, 它们不会使公式的任何部分的分母等于零。如果是这样的话, 解决方案被称为不相干, 是一种“ 假” 的解决方案, 当方程式的两边乘以一个碰巧为零的数字时, 它就被引入了。

Take the following rational equation :
::采取以下合理等式:

$\begin{aligned} x - \frac{5}{x + 3} = 12 \end{aligned}$
::x-5x+3=12 x-5x+3=12

To find the solutions of the equation, first m ultiply all parts of the equation by $\begin{aligned} (x + 3) \end{aligned}$ , the common denominator, and then simplify.
::为了找到方程的解决方案,首先将方程的所有部分乘以(x+3)、共同分母,然后简化。

\begin{aligned} x (x + 3) - 5 & = 12 (x + 3) \\ x^{2} + 3 x - 5 - 12 x - 36 & = 0 \\ x^{2} - 9 x - 41 & = 0 \\ x & = \frac{- (- 9) \pm \sqrt{(- 9)^{2} - 4 \cdot 1 \cdot (- 41)}}{2 \cdot 1} \\ x & = \frac{9 \pm 7 \sqrt{5}}{2} \end{aligned}

::x(x+3)-5=12(x+3)x2+3x-5-12x-36=0x2-9x-41=0x(-9)-(-9)-(-9)-(-)-(9)--(9)-(-)-(-)-(-)1)-(-)-(-)-(-)2-(1)-1x=9-752)

The only potential extraneous solution would have been -3 since that is the number that makes the denominator of the original equation zero. Therefore , both answers are possible.
::唯一潜在的外部解决方案是 - 3,因为这是使原始方程式零分母的数字。因此,两种答案都是可能的。

Examples
::实例

Example 1
::例1

Earlier, you were asked to account for the extra solutions introduced when both sides of an equation are multiplied by a variable . In order to deal with the possible extra solutions, you must check each solution to see if it makes the denominator of any fraction in the original equation zero. If it does, it is called an extraneous solution.
::早些时候, 当一个方程的两边乘以一个变量时, 您被要求解释引入的额外解决方案。为了处理可能的附加解决方案, 您必须检查每个解决方案, 以确定它是否在初始方程零中生成了任何分数的分母。如果是的话, 它被称为一种不相干解决方案。

Example 2
::例2

Solve the following rational equation
::解决以下合理等式

$\begin{aligned} \frac{3 x}{x + 4} - \frac{1}{x + 2} = - \frac{2}{x^{2} + 6 x + 8} \end{aligned}$
::3x+4 - 1x+22x2+6x+8

Multiply each part of the equation by the common denominator of $\begin{aligned} x^{2} + 6 x + 8 = (x + 2) (x + 4) \end{aligned}$ .
::用x2+6x+8=(x+2)(x+4)的公分母乘以方程的每个部分。

\begin{aligned} (x + 2) (x + 4) [\frac{3 x}{x + 4} - \frac{1}{x + 2}] & = [\frac{- 2}{(x + 2) (x + 4)}] (x + 2) (x + 4) \\ 3 x (x + 2) - (x + 4) & = - 2 \\ 3 x^{2} + 6 x - x - 2 & = 0 \\ 3 x^{2} + 5 x - 2 & = 0 \\ (3 x - 1) (x + 2) & = 0 \\ x & = \frac{1}{3}, - 2 \end{aligned}

x+2)(x+4)[3xx+4-1x+2][3xx+4-1x+2]=[-2(x+2)(x+2)(x+4)](x+2)(x+4)3x(x+2)-(x+2)-(x+4)23x2+6x-x-2=032x2+5x-2=0(3x-1)(x+2)=0x=13,-2

Note that -2 is an extraneous solution. The only actual solution is $\begin{aligned} x = \frac{1}{3} \end{aligned}$ .
::请注意 -2 是一个不相干的解决办法。唯一的实际解决办法是 x=13 。

Example 3
::例3

Solve the following rational equation for $\begin{aligned} y \end{aligned}$ .
::解决y的以下合理等式。

$\begin{aligned} x = 2 + \frac{1}{2 + \frac{1}{y + 1}} \end{aligned}$
::x=2+12+1y+1

This question can be done multiple ways. You can use the clearing fractions technique twice.
::这个问题可以通过多种方式解决。您可以两次使用清除分数技术。

\begin{aligned} (2 + \frac{1}{y + 1}) x & = [2 + \frac{1}{2 + \frac{1}{y + 1}}] (2 + \frac{1}{y + 1}) \\ 2 x + \frac{x}{y + 1} & = 2 (2 + \frac{1}{y + 1}) + 1 \\ 2 x + \frac{x}{y + 1} & = 4 + \frac{2}{y + 1} + 1 \\ (y + 1) [2 x + \frac{x}{y + 1}] & = [5 + \frac{2}{y + 1}] (y + 1) \\ 2 x (y + 1) + x & = 5 (y + 1) + 2 \\ 2 x y + 2 x + x & = 5 y + 5 + 2 \end{aligned}

2+1y+1+1x=[2+12+1+1y+1+11] (2+1y+1+1) 2+2xxx+1=2(2+1y+1) +12x+1+4+2y+1+1+1(y+1) 1) [2x+2x+1+1+1+1] =[5+2y+2y+1] (y+1+1)+x=5+1] (y+1+1+1+1)+x=5(y+1)+x=5+5x+2

Now just get the $\begin{aligned} y \end{aligned}$ variable to one side of the equation and everything else to the other side.
::现在只要把 Y 变量放到方程的一边其它的都放到另一边

\begin{aligned} 2 x y - 5 y & = - 3 x + 7 \\ y (2 x - 5) & = - 3 x + 7 \\ y & = \frac{- 3 x + 7}{2 x - 5} \end{aligned}

::2xy- 5y_ 3x+7y( 2x- 5) @3x+7y @3x+7y}3x+72x- 5

Example 4
::例4

Solve the following rational equation.
::解决以下合理的等式。

$\begin{aligned} \frac{3 x}{x - 5} + 4 = x \end{aligned}$
::3xx-5+4=x

\begin{aligned} 3 x + 4 x - 20 & = x^{2} - 5 x \\ 0 & = x^{2} - 12 x + 20 \\ 0 & = (x - 2) (x - 10) \\ x & = 2, 10 \end{aligned}

::3x+4x-20=x2-5x0=x2-12x+200=(x-2)(x-10x=2,10)x=2,10

Neither solution is extraneous.
::这两种解决办法都不是无关紧要的。

Example 5
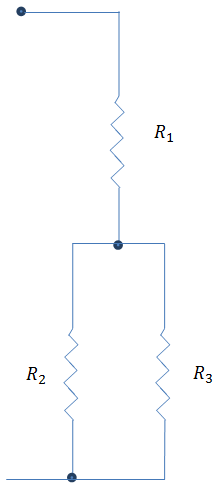
::例5

In electrical circuits, resistance can be solved for using rational expressions. This is an electric circuit diagram with three resistors. The first resistor $\begin{aligned} R_{1} \end{aligned}$ is run in series to the other two resistors $\begin{aligned} R_{2} \end{aligned}$ and $\begin{aligned} R_{3} \end{aligned}$ which are run in parallel. If the total resistance $\begin{aligned} R \end{aligned}$ is 100 ohms and $\begin{aligned} R_{1} \end{aligned}$ and $\begin{aligned} R_{3} \end{aligned}$ are each 22 ohms, what is the resistance of $\begin{aligned} R_{2} \end{aligned}$ ?
::在电路中,抗力可以用理性表达方式解答。这是一个配有三种抗体的电路图。第一种抗体R1是同时运行的其他两种抗体R2和R3的系列运行。如果总抗力R是100 ohms,R1和R3是每22 ohms,那么R2的抗力是什么?

The equation of value is:
::价值方程式是:

\begin{aligned} R = R_{1} + \frac{R_{2} R_{3}}{R_{2} + R_{3}} \end{aligned}

::R=R1+R2R3+R3

$\begin{aligned} R = R_{1} + \frac{R_{2} R_{3}}{R_{2} + R_{3}} \end{aligned}$
::R=R1+R2R3+R3

\begin{aligned} 100 & = 22 + \frac{x \cdot 22}{x + 22} \\ 78 (x + 22) & = 22 x \\ 78 x + 1716 & = 22 x \\ 56 x & = - 1716 \\ x & = - 30.65 \end{aligned}

::100=22+x_22x+22x22x2278(x+22)=22x78x+1716=22x56x_1716x_1716x_30.65

A follow up question would be to ask whether or not ohms can be negative which is beyond the scope of this text.
::一个后续问题是,问一问奥赫是否可能是消极的,这超出了本案文的范围。

Summary

Solving rational equations involves extending techniques used for solving equations with fractions, such as multiplying through by the denominator to clear the fraction.
::合理方程式的解决涉及扩大用来用分数解方程式的技术,例如通过分数乘以分数来清除分数。

To solve a rational equation, first transform it into a polynomial equation by multiplying the entire equation by the common denominator of all the rational expressions.
::为了解决一个理性的等式,首先将它变成一个多元的等式, 将整个等式乘以所有理性表达方式的共同分母。

If a solution makes the denominators of any part of the original equation equal to zero, it is considered extraneous and should be discarded.
::如果一个解决办法使原始方程的任何部分的分母等于零,它就被视为不相干,应予抛弃。

Review
::回顾

Solve the following rational equations. Identify any extraneous solutions.
::解决以下的理性方程式。找出任何不相干的解决办法。

$\begin{aligned} \frac{2 x - 4}{x} = \frac{16}{x} \end{aligned}$
::2 - 4x=16x

$\begin{aligned} \frac{4}{x + 1} - \frac{x}{x + 1} = 2 \end{aligned}$
::4x+1 -xx+1=2

$\begin{aligned} \frac{5}{x + 3} + \frac{2}{x - 3} = 1 \end{aligned}$
::5x+3+2x-3=1

$\begin{aligned} \frac{3}{x - 4} - \frac{5}{x + 4} = 6 \end{aligned}$
::3x-4-5x+4=6 3x-4-5x+4=6

$\begin{aligned} \frac{x}{x + 1} - \frac{6}{x + 2} = 4 \end{aligned}$
::xx+1-6x+2=4

$\begin{aligned} \frac{x}{x - 4} - \frac{4}{x - 4} = 8 \end{aligned}$
::xx - 4 - 4x - 4 - 4=8

$\begin{aligned} \frac{4 x}{x - 2} + 3 = 1 \end{aligned}$
::4xx-2+3=1

$\begin{aligned} \frac{- 2 x}{x + 1} + 6 = - x \end{aligned}$
::-2xx+1+6xx

$\begin{aligned} \frac{1}{x + 2} + 1 = - 2 x \end{aligned}$
::1x2+1+2+1#%2x

$\begin{aligned} \frac{- 6 x - 3}{x + 1} - 3 = - 4 x \end{aligned}$
::- 6x-3x+1-3_4x

$\begin{aligned} \frac{x + 3}{x} - \frac{3}{x + 3} = \frac{6}{x^{2} + 3 x} \end{aligned}$
::x+3x-3x+3=6x2+3x

$\begin{aligned} \frac{x - 4}{x} - \frac{2}{x - 4} = \frac{8}{x^{2} - 4 x} \end{aligned}$
::x-4x-2x-4=8x2-4x

$\begin{aligned} \frac{x + 6}{x} - \frac{2}{x + 6} = \frac{12}{x^{2} + 6 x} \end{aligned}$
::x+6x-2x+6=12x2+6x

$\begin{aligned} \frac{x + 5}{x} - \frac{3}{x + 5} = \frac{15}{x^{2} + 5 x} \end{aligned}$
::x+5x-3x+5=15x2+5x

Explain what it means for a solution to be extraneous.
::解释一个不相干的解决办法意味着什么。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

Finding Solutions to Rational Equations ::找到合理等式的解决方案

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)