超双

播放段落

Hyperbolas can be oriented so that they open side to side or up and down.  One of the most common mistakes that you can make is to forget which way a given hyperbola should open.  What are some strategies to help?
::Hyperbolas可以调整方向,让它们从侧面向上或向下打开。最常见的错误之一是忘记某一双曲线应该以哪种方式打开。有什么策略可以帮助呢?

播放段落

Graphing Hyperbolas
::超分层图

播放段落

A hyperbola has two foci . For every point on the hyperbola, the difference of the distances to each foci is constant.  This is what defines a hyperbola.  The graphing form of a hyperbola that opens side to side is:
::双倍波拉有两个角度。 对于双倍波拉上的每一点, 与每个角度的距离差异是恒定的。 这就是双倍波拉的定义。 向侧打开的双倍波拉的图形形式是 :

播放段落

$\begin{align*}\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\end{align*}$
:x-h)2a2-(y-k)2b2=1

播放段落

A hyperbola that opens up and down is:
::一个向上和向下打开的双倍波拉是:

播放段落

$\begin{align*}\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1\end{align*}$
:y-k)2a2-(x-h)2b2=1

播放段落

Notice that for hyperbolas,   $\begin{align*}a\end{align*}$ goes with the positive term and  $\begin{align*}b\end{align*}$ goes with the negative term.  It does not matter which constant is larger.
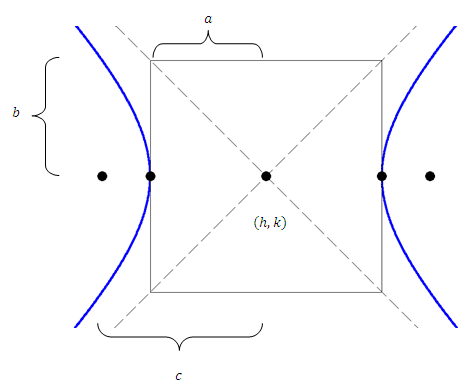
::请注意,对于超光子, 使用正值术语和 b 使用负值术语。 哪个恒定值更大并不重要 。

播放段落

When graphing, the constants  $\begin{align*}a\end{align*}$ and  $\begin{align*}b\end{align*}$ enable you to draw a rectangle around the center .  The transverse axis travels from vertex to vertex and has length $\begin{align*}2a\end{align*}$ .  The conjugate axis travels perpendicular to the transverse axis through the center and has length $\begin{align*}2b\end{align*}$ .  The foci lie beyond the vertices so the eccentricity, which is measured as $\begin{align*}e=\frac{c}{a}\end{align*}$ , is larger than 1 for all hyperbolas.  Hyperbolas also have two directrix lines that are  $\begin{align*}\frac{a^2}{c}\end{align*}$ away from the center (not shown on the image).
::当图形绘制时,常数 a 和 b 使您能够在中心周围绘制矩形。 横轴从顶部向顶部移动, 长度为 2a 。 共振轴通过中心垂直到横轴, 长度为 2b 。 顶部位于顶部之外, 因此以 e=ca 测量的偏心度大于 1 , 对所有双波las 来说, 超双波las 的偏心度大于 1 。 Hyperbolas 也有两条直径直线, 离中心有 A2c 距离( 未显示在图像上 ) 。

播放段落

The focal radius is $\begin{align*}a^2+b^2=c^2\end{align*}$ .
::焦半径为a2+b2=c2。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked how to determine the direction that a hyperbola opens. The best strategy to remember which direction the hyperbola opens is often the simplest.  Consider the hyperbola $\begin{align*}x^2-y^2=1\end{align*}$ . This hyperbola opens side to side because  $\begin{align*}x\end{align*}$ can clearly never be equal to zero.  This is a basic case that shows that when the negative is with the  $\begin{align*}y\end{align*}$ value then the hyperbola opens up side to side.
::早些时候,有人问您如何确定超重波拉打开的方向。 记住超重波拉打开的方向的最好策略往往是最简单的。 想想超重波拉 x2- y2= 1 。 这个超重波拉打开侧侧面, 因为 x 显然永远不能等于零 。 这是一个基本的例子, 表明当负值与y值存在时, 超重波拉打开侧面。

播放段落

Example 2
::例2

播放段落

Put the following hyperbola into graphing form, list the components, and sketch it. 
::将以下的双倍波拉放入图形形式,列出部件并草图。

播放段落

$\begin{align*}9x^2-4y^2+36x-8y-4=0\end{align*}$
::9x2-4y2+36x-8y-4=0

播放段落

9 ( x 2 + 4 x ) − 4 ( y 2 + 2 y ) = 4 9 ( x 2 + 4 x + 4 ) − 4 ( y 2 + 2 y + 1 ) = 4 + 36 − 4 9 ( x + 2 ) 2 − 4 ( y + 1 ) 2 = 36 ( x + 2 ) 2 4 − ( y + 1 ) 2 9 = 1

$$\begin{align*}9(x^2+4x)-4(y^2+2y)&=4\\ 9(x^2+4x+4)-4(y^2+2y+1)&=4+36-4\\ 9(x+2)^2-4(y+1)^2&=36\\ \frac{(x+2)^2}{4}-\frac{(y+1)^2}{9}&=1\end{align*}$$
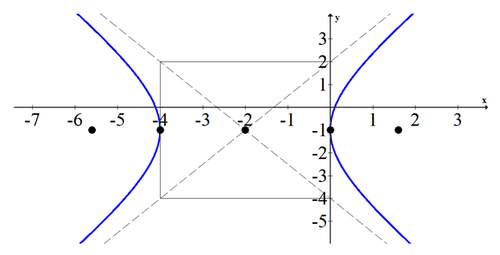
::9(x2+4x)-4(y2+2y)=49(x2+4x+4)-4(y2+2y+1)=4+36-49(x+2)-2-4(y+1)-2-4(y+1)=36(x+2)=36(x+2)24-(y+1)29=1

播放段落

Shape: Hyperbola that opens horizontally. 
::形状:水平开口的双波拉。

播放段落

Center: (-2, -1)
::中心-2,-1)

播放段落

$\begin{align*}a=2\end{align*}$
::a=2

播放段落

$\begin{align*}b=3\end{align*}$
::b=3 =

播放段落

$\begin{align*}c=\sqrt{13}\end{align*}$
::13

播放段落

$\begin{align*}e=\frac{c}{a}=\frac{\sqrt{13}}{2}\end{align*}$
::e=ca132

播放段落

$\begin{align*}d=\frac{a^2}{c}=\frac{4}{\sqrt{13}}\end{align*}$
::d=a2c=413

播放段落

Foci: $\begin{align*}(-2+\sqrt{13}, -1),~ ( -2-\sqrt{13} ,  -1)\end{align*}$
::成员: (-213,-1), (-213,-1)

播放段落

Vertices: (-4, -1), (0, -1)
::顶点4,4,-1),(0,-1)

播放段落

Equations of asymptotes: $\begin{align*}(y+1)=\pm \frac{3}{2}(x+2)\end{align*}$
::小数数的等同度y+1) 32(x+2)

播放段落

Note that it is easiest to write the equations of the asymptotes in point-slope form using the center and the slope.
::请注意,使用中间和斜坡以点窗体形式以点窗体写出小数方程是最容易的。

播放段落

Equations of directrices:  $\begin{align*}y=-2 \pm \frac{4}{\sqrt{13}}\end{align*}$
::电流平方:y2413

 

播放段落

Example 3
::例3

播放段落

Find the equation of the hyperbola with foci at (-3, 5) and (9, 5) and asymptotes with slopes of  $\begin{align*}\pm \frac{4}{3}\end{align*}$ . 
::查找超重波拉方位( 3, 5) 和( 9, 5) 的方位方位, 以及斜度为 +43 的单位方位方位 。

播放段落

The center is between the foci at (3, 5).  The focal radius is $\begin{align*}c=6\end{align*}$ .  The slope of the asymptotes is always the rise over run inside the box.  In this case since the hyperbola is horizontal and  $\begin{align*}a\end{align*}$ is in the  $\begin{align*}x\end{align*}$ direction the slope is $\begin{align*}\frac{b}{a}\end{align*}$ .  
::中心位于( 3, 5 ) 的角之间, 焦半径为 c=6 。 小微粒的斜坡总是在框内运行的上升。 在这种情况下, 双倍波拉是水平的, a 是向 x 方向的, 斜坡是 ba 。

播放段落

W e have the ratio $\begin{align*}\frac{b}{a}=\frac43.\end{align*}$   S o we'll say , $\begin{align*}b=b\end{align*}$  and $\begin{align*}a=\frac34b.\end{align*}$
::我们有Ba=43的比例,所以我们说,b=b和a=34b。

播放段落

We can substitute these into $\begin{align*}a^2+b^2=c^2\end{align*}$  and solve for $\begin{align*}b:\end{align*}$
::我们可以将这些替换为 a2+b2=c2, 并解决 b:

播放段落

$$\begin{align*}a^2+b^2&=c^2\\ \left(\frac34b\right)^2+(b)^2&=(6)^2\\ \frac{9}{16}b^2+b^2&=36\\ \frac{9}{16}b^2+\frac{16}{16}b^2&=36\\ \frac{25}{16}b^2&=36\\ b^2&=36\times\frac{16}{25}\\ b^2&=\frac{576}{25}\\ b&=\sqrt{\frac{576}{25}}\\ b&=\frac{24}{5}\\\end{align*}$$
::a2+b2=c2(34b)2+(b)2=(6)2916b2+b2=36916b2+1616b2=362516b2=36b2=36b2=361625b2=361625b2=57625b=57625b=57625b=57625b=245

播放段落

When you solve for $\begin{align*}a,\end{align*}$  you get:
::当你解决一个,你得到:

播放段落

$$\begin{align*}a^2+b^2&=c^2\\ a^2+\left(\frac{24}{5}\right)^2&=(6)^2\\  a^2+\frac{576}{25}&=36\\ a^2&=\frac{900}{25}-\frac{576}{25}\\ a&=\sqrt{\frac{324}{25}}\\ a&=\frac{18}{25}\end{align*}$$
::a2+b2=c2a2+(245)2=(6)2a2+57625=36a2=900025=57625a32425a=1825

播放段落

So,  $\begin{align*}a=\frac{18}{25}\end{align*}$  and  $\begin{align*}b=\frac{24}{5}.\end{align*}$  
::所以,a=1825和b=245。

播放段落

$$\begin{align*}\frac{(x-3)^2}{\left(\frac{18}{25}\right)^2}-\frac{(y-5)^2}{\left(\frac{24}{5}\right)^2}=1\\\end{align*}$$
:x-3)2(1825)2-(y-5)2(245)2=1

播放段落

Example 4
::例4

播放段落

Find the equation of the conic that has a focus point at (1, 2), a directrix at  $\begin{align*}x=5\end{align*}$ , and an eccentricity equal to $\begin{align*}\frac{3}{2}\end{align*}$ .  Use the property that the distance from a point on the hyperbola to the focus is equal to the eccentricity times the distance from that same point to the directrix:
::查找在(1, 2) 有焦点点的二次曲线的方程、 x=5 的直线和等于 32. 的偏心度。 使用以下属性,即从超博拉点到焦点点的距离等于从同一点到直线点的偏心度乘数:

播放段落

$\begin{align*}\overline{PF}=e \overline{PD}\end{align*}$
::你的父亲

播放段落

This relationship bridges the gap between which have eccentricity less than one and hyperbolas which have eccentricity greater than one.  When eccentricity is equal to one, the shape is a parabola .
::这种关系弥合了偏心性小于1和偏心性大于1的超高代谢之间的鸿沟。 当偏心性等于1时,形状就是一个抛物线。

播放段落

$\begin{align*}\sqrt{(x-1)^2+(y-2)^2}=\frac{3}{2}\sqrt{(x-5)^2}\end{align*}$
:x--1)2+(y-2)2=32(x-5)2

播放段落

Square both sides and rearrange terms so that it is becomes a hyperbola in graphing form. 
::方形两侧和重新排列的词义, 使其在图形形式中变成双波形 。

播放段落

$\begin{align*}x^2 -2x+1+(y-2)^2&=\frac94(x^2-10x+25)\\ x^2-2x+1+(y-2)^2&=\left(\frac94x^2-\frac{90}{4}x+\frac{255}{4}\right)\\ x^2-\frac94x^2-2x+\frac{90}{4}x+1-\frac{225}{4}+(y-2)^2&=0\\ -\frac54x^2+\frac{82}{4}x-\frac{221}{4}+(y-2)^2&=0\\ -5x^2+82x-221+4(y-2)^2&=0\\ -5x^2+82x+4(y-2)^2&=221\\ -5\left(x^2-\frac{82}{5}x\right)+4(y-2)^2&=221\\ \\ \\ -5\left(x^2-\frac{82}{5}x+\left(\frac{82}{5}\right)^2\right)+4(y-2)^2&=221+\left(-5\times\left(\frac{82^2}{5^2}\right)\right)\\ -5\left(x^2-\frac{82}{5}\right)^2+4(y-2)^2&=221-\frac{82^2}{5}\\ -5\left(x^2-\frac{82}{5}\right)^2+4(y-2)^2&=\frac{1105}{5}-\frac{6724}{5}\\ -5\left(x^2-\frac{82}{5}\right)^2+4(y-2)^2&=-\frac{5,619}{5}\\ \frac{-5\left(x^2-\frac{82}{5}\right)^2}{\left(-\frac{5,619}{5}\right)}+\frac{4(y-2)^2}{\left(-\frac{5,619}{5}\right)}&=1\\ \frac{\left(x^2-\frac{82}{5}\right)^2}{\frac{5,619}{25}}-\frac{(y-2)^2}{\frac{5,619}{20}}&=1\\\end{align*}$
::2-2-2-2-2-2x+1-2-2-2-2-2-2-2-2-2-2-2-2-2(94x2-904x+2554)x-2-2-2(94x2-904x+252-2)2=(94x2-94x2-904x+904x+1-2254xx2-942-292x-2-2x-2x-2904x+1-2254-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2-2(94x-2-904x-904x+1-2-2-2-2-2-2-2-2-2-2-25-2-202-2041414+(y-2-2)2-2-2-2-2-2-2-2-2,2-2-2-2-9-2,2-2-2-2-2-221-2-2-2-2-2-2-2-2-2-221(y-2-2-2)-221+5(-5(5(8(82,82,825252))-5(5,19(192,192,192,192,192,192,19,2,2,2,2,2,2,2,2,2,2,2,19,19,19,19,19,19,2,2,2,2,19,19,19,2,19,19,19,19,19,19,19,2,2,2,2,2,2,2,5,5,5,5,5,5,2,5,5,5,5,5,5,5,2,2,2,5,5,2,5,5,5,2,2,5,5,5,5,5,5,5,5,5,5,2,5,5,5,5,5,5,5,2,2,2,5,5,5,5,5,5,5,5,5,5,2,2,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,2,5,5,5,5,5,2

播放段落

Example 5
::例5

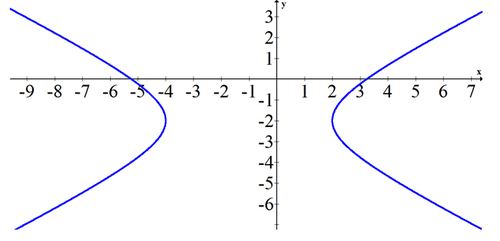
播放段落

Given the following graph, estimate the equation of the conic.
::根据下图,估计二次曲线的方程。

播放段落

Since exact points are not marked, you will need to estimate the slope of asymptotes to get an approximation for  $\begin{align*}a\end{align*}$ and $\begin{align*}b\end{align*}$ . The slope seems to be about $\begin{align*}\pm \frac{2}{3}\end{align*}$ .  The center seems to be at (-1, -2).  The transverse axis is 6 which means $\begin{align*}a=3\end{align*}$ .
::由于未标出精确点, 您需要估计小行星的斜度, 才能得出 a 和 b 的近似值。 斜度似乎是 + 23 。 中心似乎在 (-1 - 2) , 横轴是 6 , 这意味着 a= 3 。

播放段落

$\begin{align*}\frac{(x+1)^2}{9}-\frac{(y+2)^2}{4}=1\end{align*}$
:x+1)29-(y+2)24=1