要查找限制的表格

播放段落

Calculators such as the TI-84 have a table view that allows you to make extremely educated guesses as to what the limit of a function will be at a specific point, even if the function is not actually defined at that point. 
::诸如 TI-84 等计算器的表格视图可以让您对函数在某个特定点的限度进行极具教育性的猜测,即使该函数当时没有实际定义。

播放段落

How could you use a table to calculate the following limit?
::您如何使用表格计算下限 ?

播放段落

$\begin{array}{r}\underset{x\to -1}{lim}\frac{x^2+3x+2}{x+1}\end{array}$
::立方公尺#% 1x2+3x+2x+1

播放段落

Using Tables to Find Limits
::使用表格查找限制

播放段落

If you were given the following information organized in a table, how would you fill in the center column?
::如果在表格中提供以下信息,您如何填写中列 ?

3.9	3.99	3.999		4.001	4.01	4.1
12.25	12.01	12.00001		11.99999	11.99	11.75

播放段落

It would be logical to see the and notice how the top row approaches the number 4 from the left and the right. It would also be logical to notice how the bottom row approaches the number 12 from the left and the right. This would lead you to the conclusion that the limit of the function represented by this table is 12 as the top row approaches 4. It would not matter if the value at 4 was undefined or defined to be another number like 17, the pattern tells you that the limit at 4 is 12.
::顺理成章地看到并注意最上列如何从左和右走第4号。 也顺理成章地注意到最下行如何从左和右走第12号。 这将导致你得出以下结论:本表所代表的函数的极限是12,而上行的界限是4。 如果4号的数值没有定义或定义为17号, 则无关紧要, 该模式告诉你, 4号的界限是12。

播放段落

Using tables to help evaluate limits numerically requires this type of logic.  Numerically is a term used to describe one of several different representations in mathematics. It refers to tables where the actual numbers are visible. 
::使用表格帮助评估限值, 数值要求这种逻辑类型。 数字是一个用来描述数学中几种不同表达方式之一的术语, 它指的是显示实际数字的表格 。

播放段落

To estimate the limit   $\begin{array}{r}\underset{x\to 2}{lim}\frac{x-2}{x^2-x-2}\end{array}$ , complete the table:
::为估计Limx%2x-2x2-x-2的限值,填写以下表格:

$\begin{array}{r}x\end{array}$	1.9	1.99	1.999	2.001	2.01	2.1
$\begin{array}{r}f(x)\end{array}$

播放段落

While it is not necessary to use the table feature in the calculator, it is very efficient. 
::虽然计算器中不需要使用表格特征,但效率很高。

播放段落

To use a table on your calculator to evaluate a limit:
::要使用计算器上的表格来评价限制值:

播放段落
1. Enter the function on the $\begin{array}{r}y=\text{screen}\end{array}$
   ::输入 Y=屏幕上的函数
播放段落
2. Go to table set up and highlight “ask” for the independent variable
   ::转到设置的表格并突出显示独立变量的“询问”
播放段落
3. Go to the table and enter values close to the number that $\begin{array}{r}x\end{array}$  approaches
   ::跳到表格,输入接近x 位数的值

播放段落

Another option is to substitute the given $\begin{array}{r}x\end{array}$ values into the expression $\begin{array}{r}\frac{x-2}{x^2-x-2}\end{array}$ and record your results. Either way, the completed table is as follows.
::另一个选项是将给定的 x 值替换为表达式 x-2x2-x-2 并记录您的结果。无论哪种方式,填写后的表格如下。

$\begin{array}{r}x\end{array}$	1.9	1.99	1.999	2.001	2.01	2.1
$\begin{array}{r}f(x)\end{array}$	0.34483	0.33445	0.33344	0.33322	0.33223	0.32258

播放段落

The evidence suggests that the limit is $\begin{array}{r}\frac{1}{3}\end{array}$ .
::证据表明,限额是13。

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked to find the limit of   $\begin{array}{r}\underset{x\to -1}{lim}\frac{x^2+3x+2}{x+1}\end{array}$ .  When you enter values close to -1 in the table you get $\begin{array}{r}y\end{array}$  values that are increasingly close to the number 1. This implies that the limit as $\begin{array}{r}x\end{array}$  approaches -1 is 1. Notice that when you evaluate the function at -1, the calculator produces an error. This should lead you to the conclusion that while the function is not defined at  $\begin{array}{r}x=-1\end{array}$  , the limit does exist.
::早些时候, 您被要求查找 limx% 1x2+3x+2x+1 的限值。 当您在表格中输入接近 -1 的值时, 您得到的 y 值越来越接近数字 1 。 这意味着, x 接近 - 1 的限值是 1 。 注意 当您在 - 1 处评估函数时, 计算器产生错误 。 这应该导致您得出这样的结论: 虽然函数没有在 x\% 1 处定义, 但限制是存在的 。

播放段落

Example 2
::例2

播放段落

Complete the table and use the result to estimate the limit.
::填写表格并使用结果估算限额。

播放段落

$\begin{array}{r}\underset{x\to 2}{lim}\frac{x-2}{x^2-4}\end{array}$
::limx% 2x-2x2-2- 4

$\begin{array}{r}x\end{array}$	1.9	1.99	1.999	2.001	2.01	2.1
$\begin{array}{r}f(x)\end{array}$

播放段落

You can trick the calculator into giving a very exact answer by typing in 1.999999999999 because then the calculator rounds instead of producing an error.
::您可以在 1 9999999999999中打字, 欺骗计算器给出非常准确的答案, 因为随后的计算器回合而不是产生错误 。

$\begin{array}{r}x\end{array}$	1.9	1.99	1.999	2.001	2.01	2.1
$\begin{array}{r}f(x)\end{array}$	0.25641	0.25063	0.25006	0.24994	0.24938	0.2439

播放段落

The evidence suggests that the limit is $\begin{array}{r}\frac{1}{4}\end{array}$ .
::证据表明,限额是14。

播放段落

Example 3
::例3

播放段落

Complete the table and use the result to estimate the limit.
::填写表格并使用结果估算限额。

播放段落

$\begin{array}{r}\underset{x\to 0}{lim}\frac{\sqrt{x+3}-\sqrt{3}}{x}\end{array}$
::limx=0x+3-3-3x

$\begin{array}{r}x\end{array}$	-0.1	-0.01	-0.001	0.001	0.01	0.1
$\begin{array}{r}f(x)\end{array}$

$\begin{array}{r}x\end{array}$	-0.1	-0.01	-0.001	0.001	0.01	0.1
$\begin{array}{r}f(x)\end{array}$	0.29112	0.28892	0.2887	0.28865	0.28843	0.28631

播放段落

The evidence suggests that the limit is a number between 0.2887 and 0.28865. When you learn to find the limit analytically , you will know that the exact limit is  $\begin{array}{r}\frac{1}{2}\cdot 3\frac{1}{2}\approx 0.2886751346\end{array}$ .
::证据表明,极限值在0.2887至0.288665之间。当您通过分析找到极限值时,您就会知道准确的极限值是123120.2886751346。

播放段落

Example 4
::例4

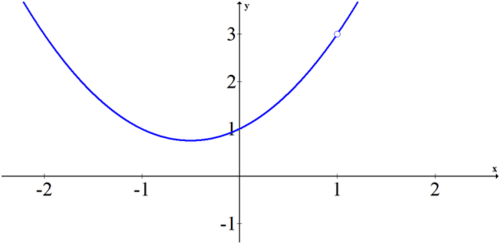
播放段落

Graph the following function and the use a table to verify the limit as $\begin{array}{r}x\end{array}$ approaches 1.
::以下图解函数和使用表格来验证x 方向 1 的极限。

播放段落

$\begin{array}{r}f(x)=\frac{x^3-1}{x-1},x\ne 1\end{array}$
:xx) =x3 - 1x - 1, x1

播放段落

$\begin{array}{r}\underset{x\to 1}{lim}f(x)=3\end{array}$ . This is because when you factor the numerator and cancel common factors, the function becomes a quadratic with a hole at the point $\begin{array}{r}(1,3)\end{array}$ .
::limx1f(x)=3. 这是因为当您乘以分子和取消共同系数时,函数就变成了一个在点(1,3)上有一个洞的四方形函数。

播放段落

You can verify the limit in the table.
::您可以在表格中验证限制 。

$\begin{array}{r}x\end{array}$	$\begin{array}{r}f(x)\end{array}$
.75	2.3125
.9	2.71
.99	2.9701
.999	2.997
1	Error
1.001	3.003
1.01	3.0301
1.1	3.31
1.25	3.8125

播放段落

Example 5
::例5

播放段落

Estimate the limit numerically.
::以数值估计限额。

播放段落

$\begin{array}{r}\underset{x\to 0}{lim}\frac{\left[\frac{4}{x+2}\right]-2}{x}\end{array}$
::limx%0[4x+2]-2x

$\begin{array}{r}x\end{array}$	-0.1	-0.01	-0.001	0.001	0.01	0.1
$\begin{array}{r}f(x)\end{array}$	0.20526	0.02005	0.002	-0.002	-0.02	-0.1952

播放段落

$\begin{array}{r}\underset{x\to 0}{lim}f(x)=0\end{array}$
::limx0f(x)=0

Summary

播放段落 Tables can be used to find the limit of a function at a specific point, even if the function is not defined at that point. ::表格可用于在特定点找到函数的极限,即使该函数当时没有定义。 播放段落 Numerically refers to tables where the actual numbers are visible ::数字指实际数字可见的表格 播放段落 To estimate the limit, complete the table by entering values close to the number that the function approaches. ::为估计限额,填写表格时输入接近该函数所接近的数值。

播放段落

Review
::回顾

播放段落

Estimate the following limits numerically.
::以数字方式估计以下限度。

播放段落

1. $\begin{array}{r}\underset{x\to 5}{lim}\frac{x^2-25}{x-5}\end{array}$
::1. limx=5x2-2-25x-5

播放段落

2. $\begin{array}{r}\underset{x\to -1}{lim}\frac{x^2-3x-4}{x+1}\end{array}$
::2. limx%1x2-3x-4x+1

播放段落

3. $\begin{array}{r}\underset{x\to 2}{lim}\frac{x^3-5x^2+2x-4}{x^2-3x+2}\end{array}$
::3. limx%2x3 - 5x2+2x-4x2 - 3x+2

播放段落

4. $\begin{array}{r}\underset{x\to 0}{lim}\frac{\sqrt{x+2}-\sqrt{2}}{x}\end{array}$
::4. limx=0x+2-2-2x

播放段落

5. $\begin{array}{r}\underset{x\to 3}{lim}\left(\frac{1}{x-3}-\frac{9}{x^2-9}\right)\end{array}$
::5. 立正3(1x-3-3-9x2-9)

播放段落

6. $\begin{array}{r}\underset{x\to 2}{lim}\frac{x^2+5x-14}{x-2}\end{array}$
::6. limx%2x2+5x-14x-2

播放段落

7. $\begin{array}{r}\underset{x\to 1}{lim}\frac{x^2-8x+7}{x-1}\end{array}$
::7. limx=1x2-8x+7x-1

播放段落

8. $\begin{array}{r}\underset{x\to 0}{lim}\frac{\sqrt{x+5}-\sqrt{5}}{x}\end{array}$
::8. limx=0x+5-5-5x

播放段落

9. $\begin{array}{r}\underset{x\to 9}{lim}\frac{\sqrt{x}-3}{x-9}\end{array}$
::9. limx%9x-3x-9

播放段落

10. $\begin{array}{r}\underset{x\to 0}{lim}\frac{x^2+5x}{x}\end{array}$
::10. limx=0x2+5xxx

播放段落

11. $\begin{array}{r}\underset{x\to -3}{lim}\frac{x^2-9}{x+3}\end{array}$
::11. limx=%3x2-9x+3

播放段落

12. $\begin{array}{r}\underset{x\to 4}{lim}\frac{\sqrt{x}-2}{x-4}\end{array}$
::12. 立方 4x-2x-4

播放段落

13. $\begin{array}{r}\underset{x\to 1}{lim}\frac{\sqrt{x+3}-2}{x-1}\end{array}$
::13. limx1x+3-2x-1

播放段落

14. $\begin{array}{r}\underset{x\to 5}{lim}\frac{x^2-25}{x^3-125}\end{array}$
::14. 立方×5x2-2-25x3-125

播放段落

15. $\begin{array}{r}\underset{x\to -1}{lim}\frac{x-2}{x+1}\end{array}$
::15. limx%1x-2x+1

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。