节: 如果- 然后声明 | 16.2 如果当时发言

章节大纲

If-then statements are very common outside formal mathematics. In many cases, your familiarity with these types of statements will help you to interpret their meaning and truth value . In other cases, the truth value of some statements may be unclear without a formal understanding of logic. Consider the following two statements:
::如果当时的言论在正式数学之外非常常见。在许多情况下,你熟悉这些类型的言论会帮助你解释其含义和真相价值。在其他情况下,有些言论的真相价值可能不清楚,而没有正式的逻辑理解。考虑以下两种言论:

If it rains today then you will stay at home and read a book.
::如果今天下雨了那你就呆在家里看书吧

You stayed at home and read a book.
::你留在家里看书

Did it or did it not rain?
::是下雨还是没有下雨?

If-Then Statements
::如果- 然后声明

A mathematical set is just a group of things. The group can include anything: letters, numbers, objects or monkeys. Set theory focuses on the relationships between sets as they overlap or are completely within each other. For the purposes of if-then statements, set theory provides a perfect framework in which to reason.
::数学集只是一组事物。组群可以包含任何东西: 字母、数字、对象或猴子。组集的理论侧重于各组群之间的关系, 因为它们重叠或完全在彼此内部。组集的理论可以提供一个完美的框架, 用来说明理由。

Consider set $\begin{aligned} P \end{aligned}$ and set $\begin{aligned} Q \end{aligned}$ that are just collections of things represented by circles. If something is not in the set, then it is not in the circle .
::考虑设置 P 和设置 Q , 它们只是以圆为代表的事物的集合。如果某东西不在集中, 那么它就不会在圆中。

In this case set $\begin{aligned} P \end{aligned}$ is a subset of set $\begin{aligned} Q \end{aligned}$ since it is entirely included within set $\begin{aligned} Q \end{aligned}$ . Mathematically we write the statement “ $\begin{aligned} P \end{aligned}$ is a subset of $\begin{aligned} Q \end{aligned}$ ” as:
::在这种情况下,设定的P是设定的Q的一个子集,因为它完全包含在设定的Q中。

$\begin{aligned} P \subseteq Q \end{aligned}$
::

This can be translated to an if-then statement , and simplified using symbols:
::这可以翻译为 " 如果当时 " 的语句,并简化使用符号:

If it is an element in $\begin{aligned} P \end{aligned}$ , then it is an element in $\begin{aligned} Q \end{aligned}$ .
::如果是P的一个元素,就是Q的一个元素。

If $\begin{aligned} P \end{aligned}$ , then $\begin{aligned} Q \end{aligned}$ .
::如果是P,那么是Q。

$\begin{aligned} P \to Q \end{aligned}$
::

If-then statements are examples of conditional statements . Sometimes conditional statements are written without an “if” or a “then”, but can be rewritten. The “if” part of the statement (represented by $\begin{aligned} P \end{aligned}$ above) is called the hypothesis, antecedent or protasis . The “then” part of the statement (represented by $\begin{aligned} Q \end{aligned}$ above) is called the conclusion , consequent or apodosis .
::如果当时的声明是有条件声明的例子,有时有条件声明是在没有“如果”或“如果”或“当时”的情况下写的,但可以改写,声明的“如果”部分(由上文P部分代表)称为假设、先前或预证,声明的“当时”部分(由上文Q部分代表)称为结论、结果或假设。

In order to precisely define the truth value of a conditional statement , we need to consider the four different combinations of the truth value for $\begin{aligned} P \end{aligned}$ and $\begin{aligned} Q \end{aligned}$ in relation to the diagram
::为了准确界定有条件陈述的真相价值,我们需要结合图表,考虑P和Q的真相价值的四种不同组合。

If $\begin{aligned} P \end{aligned}$ is true, then $\begin{aligned} Q \end{aligned}$ is true. This statement is true because if an object is inside circle $\begin{aligned} P \end{aligned}$ , then it is definitely inside circle $\begin{aligned} Q \end{aligned}$ .
::如果 P 是真实的, 那么Q 是真实的。此语句是真实的。因为如果一个对象在 P 圆内, 那么它肯定在 Q 圆内。

If $\begin{aligned} P \end{aligned}$ is true, then $\begin{aligned} Q \end{aligned}$ is false. This statement is false because there is no possible way an object could be inside circle $\begin{aligned} P \end{aligned}$ and yet outside circle $\begin{aligned} Q \end{aligned}$ .
::如果 P 是真实的, 那么Q 是虚假的。此声明是虚假的, 因为不可能有对象在 P 圆圈内, 而在 Q 圆圈外。

If $\begin{aligned} P \end{aligned}$ is false, then $\begin{aligned} Q \end{aligned}$ is true. This statement is considered true because if an object is outside circle $\begin{aligned} P \end{aligned}$ then it may or may not be in circle $\begin{aligned} Q \end{aligned}$ . There is no contradiction.
::如果 P 是假的, 那么Q 是真实的。此语句被认为是真实的, 因为如果一个对象在 P 圆圈之外, 那么它可能是或者不是在 Q 圆圈里。不存在矛盾。

If $\begin{aligned} P \end{aligned}$ is false, then $\begin{aligned} Q \end{aligned}$ is false. This statement is also considered true because if an object is outside circle $\begin{aligned} P \end{aligned}$ , then it can be outside circle $\begin{aligned} Q \end{aligned}$ . Like the previous statement, there is no contradiction.
::如果 P 是假的, 那么Q 是假的。这个声明也被认为是真实的, 因为如果一个对象在 P 圈之外, 那么它也可以在 Q 圈之外。和先前的声明一样, 没有矛盾。

The truth values of the four combinations can be summarized in a truth table. Recall that are extremely useful for summarizing complicated logical sentences and identifying whether the statements are true or false.
::四个组合的真相价值可以在一个真相表格中概括。回顾对于总结复杂的逻辑句子和确定这些陈述是真实的还是虚假的极为有用。

$\begin{aligned} P \end{aligned}$	$\begin{aligned} Q \end{aligned}$	$\begin{aligned} P \to Q \end{aligned}$
T	T	T
T	F	F
F	T	T
F	F	T

Note that a conditional statement is only false when the hypothesis is true and the conclusion is false . Also note that any conditional statement with a false hypothesis is trivially true. The following statement is trivially true because the hypothesis is false.
::请注意,有条件声明只有在假设属实且结论属虚假时才是虚假的。请注意,任何带有虚假假设的有条件声明都是虚伪的。以下声明仅属虚伪,因为假设属虚伪。

If pigs can fly then butterflies eat elephants.
::如果猪能飞,蝴蝶就吃大象。

The truth of this statement confuses many people the first time they look at it. One way to frame it in your mind is to realize that a statement is false only when it results in a logical contradiction. In a world where pigs could fly perhaps butterflies could eat elephants, who knows? It would be ridiculous for a person to argue that in the hypothetical world where pigs could fly that there is no way that butterflies could eat elephants.
::这种说法的真相让许多人第一次看到它时就迷惑了。将它写进你脑中的一个方法就是认识到,只有当它导致逻辑矛盾时,声明才是假的。在猪可以飞翔的世界上,蝴蝶也许可以吃大象,谁知道呢? 一个人在假设世界里猪可以飞翔,不能吃大象,这是荒谬的。

Examples
::实例

Example 1
::例1

Earlier, you were asked if it rained given the following two statements:
::先前,有人问您是否下雨,因为有以下两种说法:

If it rains today then you will stay at home and read a book.
::如果今天下雨了那你就呆在家里看书吧

You stayed at home and read a book.
::你留在家里看书

Use a diagram to represent the conditional statement.
::使用图表表示条件语句。

If it rains today then you will stay at home and read a book.
::如果今天下雨了那你就呆在家里看书吧

$\begin{aligned} P = i t r a i n s t o d a y \end{aligned}$
::P=今天的雨雨

$\begin{aligned} Q = y o u w i l l s t a y a t h o m e a n d r e a d a b o o k \end{aligned}$ .
::你会留在家里读一本书

You stayed at home and read a book. This implies that $\begin{aligned} Q \end{aligned}$ is true. According to the diagram, if an object is inside $\begin{aligned} Q \end{aligned}$ it may or may not be inside $\begin{aligned} P \end{aligned}$ . Thus, you can conclude nothing about the rain. Many people will want to incorrectly conclude that it must have rained, but conditional statements only flow in one direction.
::您留在家里阅读一本书。这意味着Q是真实的。根据图表,如果一个物体在Q内部,它可能也可能不是在P内部。因此,您无法得出关于雨水的任何结论。许多人会想错误地得出结论,它一定是下雨了,但有条件的言词只流向一个方向。

Example 2
::例2

Rewrite the following conditional statements in if-then form.
::下列有条件声明如以当时形式重写,则以当时形式重写。

If you go to the show, you will be amazed.
::如果你去看演出,你会惊讶的

Unless you buy firewood you will be cold.
::除非你买木柴否则你会很冷

Come here and you will get a present.
::来到这里,你会得到一个礼物。

Kicking a soccer ball makes it bounce.
::踢足球让球弹跳

Give me your lunch money or I’ll put you in a locker.
::把午餐钱给我不然我把你放在储物柜里

Anyone who wears orange likes Halloween.
::任何穿橙色衣服的人都喜欢万圣节

Without my sunglasses on I can’t drive.
::没有墨镜我无法开车。

Buy this product and you’ll be beautiful and popular.
::买下这个产品, 你就会变得美丽和受欢迎。

Even though these statements have words like “and”, “or” and “not” they are still just conditional statements. In each case, consider which action or event leads to another action or event.
::尽管这些声明有“和”、“或”和“不是”等字眼,但它们仍然只是有条件的声明,在每一种情况下,考虑哪些行动或事件导致另一种行动或事件。

If you go to the show, then you will be amazed.
::如果你去看演出,你会惊讶的

If you do not buy firewood, then you will be cold.
::如果你们不买柴,那末,你们将变成寒冷的。

If you come here, then you will get a present.
::如果你来到这里, 那么你会得到一个礼物。

If you kick a soccer ball, then it will bounce.
::如果你踢足球,它就会弹跳

If you don’t give me your lunch money, then I’ll put you in a locker.
::如果你不把午餐钱给我, 我就把你放在储物柜里。

If a person wears orange, then that person likes Halloween.
::如果一个人穿橙色, 那么那个人喜欢万圣节。

If I do not wear my sunglasses, then I can’t drive.
::如果我不戴墨镜,

If you buy this product, then you will be beautiful and popular.
::如果你买下这个产品,你就会变得美丽和受欢迎。

Example 3
::例3

Evaluate the truth value of the following conditional statement using a truth table.
::使用真相表评估以下有条件声明的真相价值。

If when I go somewhere I always run, then when I run I always go somewhere.
::如果我去的地方总是我跑, 那么当我跑,我总是去的地方。

This statement actually has two layers of conditional statements because both the hypothesis and the conclusion are conditional statements themselves.
::实际上,这一声明有两层条件声明,因为假设和结论本身都是有条件声明。

Let $\begin{aligned} R \end{aligned}$ be the statement “I run”.
::让R成为“我运行”的语句。

Let $\begin{aligned} S \end{aligned}$ be the statement “I go somewhere”.
::让我们说一句“我要去什么地方”。

The original sentence can be rewritten in symbols as: $\begin{aligned} (S \to R) \to (R \to S) \end{aligned}$ . To make the truth table for the sentence, start with all possible truth combinations of $\begin{aligned} S \end{aligned}$ and $\begin{aligned} R \end{aligned}$ (both true, $\begin{aligned} S \end{aligned}$ true/ $\begin{aligned} R \end{aligned}$ false, $\begin{aligned} S \end{aligned}$ false/ $\begin{aligned} R \end{aligned}$ true, both false). Then, find the truth values for each piece working up to the full sentence.
::原句可以改写为符号 : (SR) (RS) 。要绘制句子的真相表,首先要从S和R的所有可能的真相组合开始(既真实,S true/R fraud,S fraud/R true,两者都是虚假的 ) 。然后,找到每段句子的真相值,直到句子完整为止。

$\begin{aligned} S \end{aligned}$	$\begin{aligned} R \end{aligned}$	$\begin{aligned} S \to R \end{aligned}$	$\begin{aligned} R \to S \end{aligned}$	$\begin{aligned} (S \to R) \to (R \to S) \end{aligned}$
T	T	T	T	T
T	F	F	T	T
F	T	T	F	F
F	F	T	T	T

The statement is always true unless you run but do not go anywhere.
::语句总是对的,除非您运行但别去任何地方。

Example 4
::例4

If all of the following statements are true, what can you conclude?
::如果以下所有声明都属实,你能得出什么结论?

All babies are cute.
::所有的婴儿都是可爱的。

Laura likes cute people.
::劳拉喜欢可爱的人

Laura is a baby.
::劳拉是个婴儿

First translate each of the statements into conditional statements (even if they sound awkward!). This is helpful for determining an if-then chain of events.
::首先将每一份声明翻译成有条件声明(即使这些声明听起来很尴尬! ! ! ) 。这对确定当时的一连串事件很有帮助。

$\begin{aligned} A \end{aligned}$ : If a person is a baby then the person is cute.
::甲:如果一个人是婴儿,那么这个人是可爱的。

$\begin{aligned} B \end{aligned}$ : If a person is cute then Laura likes that person.
::B:如果一个人很可爱,那么劳拉喜欢这个人。

$\begin{aligned} C \end{aligned}$ : If a person is named Laura then that person is a baby.
::C:如果一个人的名字叫劳拉,那么这个人就是婴儿。

You should notice the circular structure of these three statements.
::您应通知这三份声明的循环结构。

$\begin{aligned} A \to B, B \to C, C \to A \end{aligned}$
::A_B,B_C,C_A

$\begin{aligned} A \to B \to C \to A \end{aligned}$
::阿比比西亚州

While many conclusions could be made, one conclusion about Laura is that she likes herself.
::虽然可以得出许多结论,但关于劳拉的一个结论是,她喜欢自己。

Example 5
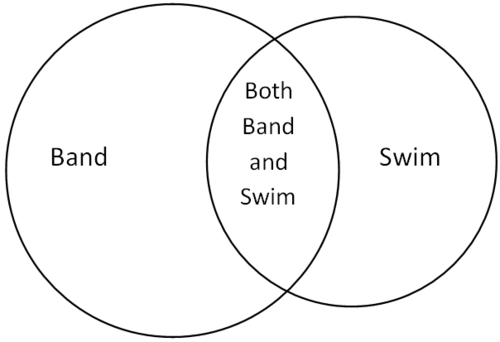
::例5

There are 53 people in the marching band and 49 people on the swim team. If 84 people belong to either or both teams, how many people are on both teams?
::游行队有53人,游泳队有49人。如果84人属于其中一队或两队,两队有多少人?

While this problem is not specific to if-then statements, it can be solved using a set theory representation and if-then logic.
::虽然这个问题并非具体针对当时的言论,但可以通过一套既定的理论表述和当时的逻辑来解决。

Students on both teams would be double counted if you simply added up the number of students in band and the number of students on the swim team.
::如果你把乐队学生人数和游泳队学生人数加在一起,两个队的学生人数将加倍计算。

$\begin{aligned} 53 + 49 = 102 \end{aligned}$

Since there are only 84 people total, then $\begin{aligned} 102 - 84 = 18 \end{aligned}$ students must have been counted twice. Therefore, there are 18 students on both squads.
::由于总人数只有84人,因此必须两次计算102-84=18名学生,因此,两个班共有18名学生。

Summary

If-then statements are examples of conditional statements, with the "if" part called the hypothesis, and the "then" part called the conclusion.
::如果当时的声明是有条件声明的例子,“如果”部分称为假设,“当时”部分称为结论。

Set theory provides a framework for reasoning about if-then statements, with subsets representing the relationship between the hypothesis and conclusion.
::" 设定理论 " 提供了一个推理框架,用于推理 " 如果当时的声明 " ,其子集代表假设与结论之间的关系。

The truth value of a conditional statement can be determined by considering four combinations of the truth values for the hypothesis and conclusion.
::有条件陈述的真相价值可以通过考虑假设和结论的四种真相价值组合来确定。

A conditional statement is only false when the hypothesis is true and the conclusion is false; any conditional statement with a false hypothesis is trivially true.
::有条件声明只有在假设属实而且结论属虚假时才是虚假的;任何带有虚假假设的有条件声明都是微不足道的。

Truth tables can be used to summarize the truth values of conditional statements and identify whether they are true or false.
::真相表可用来总结有条件陈述的真相价值,并查明这些陈述是真实的还是虚假的。

Review
::回顾

1. What are the three names for the “if” part of an if-then statement?
::1. " 如果 " 声明的 " 如果 " 部分的三种名称是什么?

2. What are the three names for the “then” part of an if-then statement?
::2. " 如果当时 " 声明的 " 当时 " 部分的三个名称是什么?

Rewrite each of the following statements in if-then form.
::下列各语句均按当时形式重写。

3. If you like Pepsi, you will like Coke.
::3. 如果你喜欢百事可乐,你会喜欢可乐。

4. Do your homework and you will get candy.
::4. 做你的功课,你会得到糖果。

5. Anyone who goes to the mall likes to shop.
::5. 任何去商场的人都喜欢购物。

6. Unless you cook dinner, you will be hungry.
::6,除非你做饭,否则你会饿死的。

7. Join this program and you will lose weight.
::7. 加入这个方案,你会减肥。

8. Shoveling snow makes your back sore.
::8. 雪雪使你的背痛。

9. Without knowing how to drive, you will not get your license.
::9. 在不知道如何开车的情况下,你将得不到驾照。

10. Be nice to your sister or you will be punished.
::对你妹妹好一点否则你将受到惩罚

11. When is the following statement false? If you are a kid, then you like pizza.
::11. 下列陈述何时是假的?如果还是个孩子,那么你喜欢披萨。

12. If all of the following statements are true, what can you conclude?
::12. 如果以下所有声明都属实,你能得出什么结论?

All kids like pizza.
::所有的孩子都喜欢比萨饼。

Sam is 8 years old.
::萨姆八岁了

8 year olds are kids.
::8岁的孩子。

13. There are 15 people in the math club and 27 people in the debate club. If 33 people belong to either or both clubs, how many people are just in the debate club?
::13. 数学俱乐部有15人,辩论俱乐部有27人,如果33人属于其中一个或两个俱乐部,那么辩论俱乐部里有多少人?

14. There are 32 people on the bus in the morning and 40 people on the bus in the afternoon. If 20 people only ride the bus in the afternoon, how many people only ride the bus in the morning?
::14. 早上有32人在公共汽车上,下午有40人在公共汽车上,如果下午只有20人坐公共汽车,早上有多少人坐公共汽车?

15. There are 24 people in your math class and 27 people in your English class. If 7 people are in your English class but not your math class, how many people are in your math class but not your English class?
::15. 数学班有24人,英语班有27人,英语班有7人,如果英语班有7人,但数学班没有,数学班有多少人,英语班没有?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

If-Then Statements ::如果- 然后声明

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)