需要衍生因素:即时变化率

播放段落

Jim took a picture of his track-star girlfriend Becca running. The two of them were discussing how they might calculate her speed at the instant that Jim snapped a photo of her. The end result of the discussion was Becca pointing out that it is not technically possible to calculate the exact speed of something in a specific instant.
::Jim拍了一张他的跟踪明星女友Becca跑动的照片。他们两人正在讨论他们如何计算Jim拍下她照片时的速度。讨论的最终结果是Becca指出,在技术上不可能在特定瞬间计算某事的确切速度。

播放段落

By now, we have explored the related concepts of limits and lines tangent to a curve, so we know it is possible to effectively calculate instantaneous speed. What process would be involved with actually calculating Becca's speed at the instant the photo was taken? What are the technical difficulties with identifying instantaneous speed?
::现在,我们已经探索了相关的界限和线条与曲线相切的概念,因此我们知道可以有效计算瞬时速度。在拍摄照片时实际计算贝卡速度需要什么过程?在确定瞬时速度方面有什么技术困难?

播放段落

Instantaneous Rate of Change
::过早变化率

播放段落

The function  $\begin{align*}{m}_{tan}\end{align*}$  that we defined in the previous concept is so important that it has its own name: the derivative.
::我们在前一个概念中定义的函数 mtan 是如此重要,以至于它有它自己的名字:衍生物。

播放段落

The Derivative
::衍生工具

播放段落

The function $\begin{align*}{m}_{tan}\end{align*}$  can also be written as  $\begin{align*}f^{\prime} (x)\end{align*}$  and is defined by the formula
::函数 mtan 也可以写成 f}(x) , 并且由公式定义

播放段落

$$\begin{align*}f^{\prime} (x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\end{align*}$$
::f_(x) = limh_0f(x+h) - f(x) h

播放段落

$\begin{align*}f^{\prime} (x)\end{align*}$ is called the derivative of $\begin{align*}f (x)\end{align*}$ with respect of $\begin{align*}x\end{align*}$ .
::f}(x) 指 x 的 f(x) 衍生物。

播放段落

The domain of $\begin{align*}f^{\prime} (x)\end{align*}$ consists of all the values of  $\begin{align*}x\end{align*}$ for which the limit exists.
::f(x) 域包含有限制的 x 的所有值 。

播放段落

Based on the discussion that we have had in the previous concept, the derivative $\begin{align*}f^\prime\end{align*}$ represents the slope of the tangent line at point $\begin{align*}x\end{align*}$ . Another way of interpreting it would be that the function  $\begin{align*}y = f(x)\end{align*}$ has a derivative  $\begin{align*}f^\prime\end{align*}$ whose value at  $\begin{align*}x\end{align*}$ is the instantaneous rate of change of  $\begin{align*}y\end{align*}$ with respect to point $\begin{align*}x\end{align*}$ .
::根据我们在前一个概念中的讨论,衍生物f 表示x点正切线的斜坡。 另一种解释方法是,函数y=f(x)具有衍生物f ,其值在x点是y相对于x点的瞬时变化速率。

播放段落

One of the two primary concepts of calculus involves calculating the rate of change of one quantity with respect to another. For example, speed is defined as the rate of displacement with respect to time. If a person travels 120 miles in 4 hours, his speed is $\begin{align*}\frac{120}{4}=30 \ mi/hr\end{align*}$ . This speed is called the average speed or the average rate of change of distance with respect to time. Of course the person who travels 120 miles at a rate of 30 mi/hr for 4 hr probably does not do so continuously. Though he probably slowed down or speed up during the 4-hour period, it does generally suffice to say that he traveled for 4 hours at an average rate of 30 miles per hour. However, if the driver strikes a tree, it would not be his average speed that determines his survival but his speed at the instant of the collision . Similarly, when a bullet strikes a target, it is not the average speed that is significant but its instantaneous speed at the moment it strikes. So here we have distinct kinds of speeds, average speed and instantaneous speed.
::微积分的两个基本概念之一涉及计算一个数量相对于另一个数量的变化速度。 例如, 速度被定义为时间迁移速度。 如果一个人在4小时内行驶120英里, 速度为120英里, 速度为120=30英里/ 英里。 这个速度被称为平均速度或距离平均变化速度。 当然, 以30英里/ 小时的速度行驶120英里, 4小时的速度可能不会持续。 尽管他可能在4小时内放慢或加快速度, 但通常只要说他以平均每小时30英里的速度行驶4小时就足够了。 但是, 如果司机撞上一棵树, 其平均速度将不是决定他的生存速度, 而是在碰撞的瞬间速度。 同样, 当子弹击中目标时, 其平均速度不是很大, 而是在撞击时的瞬间速度。 因此我们这里有不同的速度、 平均速度和瞬间速度。

播放段落

The average speed of an object is defined as the object's displacement  $\begin{align*}\triangle x\end{align*}$ divided by the time interval  $\begin{align*}\triangle t\end{align*}$ during which the displacement occurs:
::对象的平均速度定义为对象的移位 x 除以移位发生的时间间隔 t :

播放段落

$$\begin{align*}\text{Average speed}=v=\frac{\triangle x}{\triangle t}=\frac{x_1-x_0}{t_1-t_0}\end{align*}$$
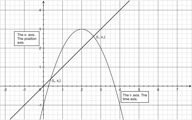
::平均速度=vxt=x1-x0t1-t0

播放段落

Notice that the points $\begin{align*}(t_0, x_0)\end{align*}$ and  $\begin{align*}(t_1, x_1)\end{align*}$ lie on the position versus time curve, as the figure below shows.
::请注意,如下图所示,点数(t0,x0)和点数(t1,x1)位于位置与时间曲线上。

播放段落

This expression is also the expression for the slope of a secant line connecting the two points. Thus we conclude that the average velocity of an object between time  $\begin{align*}t_0\end{align*}$ and  $\begin{align*}t_1\end{align*}$ is represented geometrically by the slope of the secant line connecting the two points  $\begin{align*}(t_0, x_0)\end{align*}$ and $\begin{align*}(t_1, x_1)\end{align*}$ . If we choose  $\begin{align*}t_1\end{align*}$ close to $\begin{align*}t_0\end{align*}$ , then the average velocity will closely approximate the instantaneous velocity at time $\begin{align*}t_0\end{align*}$ .
::此表达式也是连接两个点的松动线斜坡的表达式。 因此, 我们得出结论, 时间 t0 和 t1 之间的对象的平均速度由连接两个点( t0, x0) 和 ( t1, x1) 的松动线的斜坡几何代表, 如果我们选择 t1 接近 t0, 那么平均速度将接近时间 t0 的瞬时速度 。

播放段落

Geometrically, the average rate of change is represented by the slope of a secant line and the instantaneous rate of change is represented by the slope of the tangent line.
::从几何上看,平均变化率以偏移线的斜坡表示,瞬时变化率以正切线的斜坡表示。

播放段落

Average Rate of Change (such as the average velocity)
::平均变化率(如平均速度)

播放段落

The average rate of change of  $\begin{align*}y = f(x)\end{align*}$ over the time interval  $\begin{align*}[x_0, x_1]\end{align*}$ is the slope  $\begin{align*}m_{sec}\end{align*}$ of the secant line to the points  $\begin{align*}(x_0, f(x_0))\end{align*}$ and  $\begin{align*}(x_1, f(x_0))\end{align*}$ on the graph (figure a):
::y=f(x) 在时间间隔[x0,x1]中的平均变化速率(y=f(xx))是伸缩线的斜度毫塞克至图中点(x0,f(x0))和(x1,f(x0))(图a):

播放段落

$$\begin{align*}m_{sec}=\frac{f(x_1)-f(x_0)}{x_1-x_0}\end{align*}$$
::msec=f(x1)-f(x0)x1-x0

播放段落

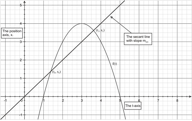
Instantaneous Rate of Change
::过早变化率

播放段落

The instantaneous rate of change of $\begin{align*}y = f(x)\end{align*}$ at the point  $\begin{align*}x_0\end{align*}$ is the slope  $\begin{align*}m_{sec}\end{align*}$ of the tangent line to the point  $\begin{align*}x_0\end{align*}$ on the graph (figure b):
::在x0点,y=f(x)的瞬时变化速率为正切线的斜度msec至图中点x0(图b):

播放段落

$$\begin{align*}m_{tan}=f^\prime(x_0)=\lim_{x_1 \to x_0} \frac{f(x_1)-f(x_0)}{t_1-t_0}\end{align*}$$
::mtan=f_(x0)=limx1_x0f(x1)-f(x0)t1-t0

播放段落

What is the the slope of the line tangent to $\begin{align*}y=x^2+5\end{align*}$ at the point on the curve $\begin{align*}x=4\end{align*}$ . What is the equation of that line? 
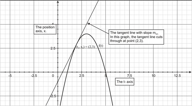
::曲线 x=4 点与 y=x2+5 相切线的斜度是多少? 该线的方程是什么?

播放段落

In the previous lesson, we showed how to calculate the derivative (the slope of the tangent) of a function of the form $\begin{align*}y=x^2-c\end{align*}$
::在前一课中,我们演示了如何计算y=x2-c 窗体函数的衍生值(正切值的斜度)

播放段落

The slope of the tangent to the curve $\begin{align*}y=x^2+5\end{align*}$ at $\begin{align*}x=4\end{align*}$ is: $\begin{align*}2(4)=8\end{align*}$
::x=4 xx=4 的曲线y=x2+5的正切斜度为: 2(4)=8

播放段落

Recall from Algebra I the “slope - intercept form” of a straight line: $\begin{align*}y=mx+b\end{align*}$ , where  $\begin{align*}m\end{align*}$ is the slope of the line.
::从代数一中回顾,y=mx+b是线的斜坡。

播放段落

Given $\begin{align*}m=8\end{align*}$ from above, we have $\begin{align*}y=8x+b\end{align*}$ . All we need is to solve for  $\begin{align*}b\end{align*}$ to have the full equation.
::根据上面的 m=8,我们有y=8x+b。我们只需要解决b 才能有全方程。

播放段落

Substitute 4 (the point we are finding the slope of) in for $\begin{align*}x\end{align*}$ in the equation of the curve $\begin{align*}y=x^2+5\end{align*}$ to identify a corresponding $\begin{align*}y\end{align*}$
::y=x2+5 的方程中 x x 的替代值 4( 我们所找到的点) , 以识别相应的 y

播放段落

$$\begin{align*}y&=(4)^2+5\\ y&=21\end{align*}$$
::y=(4)2+5y=21

播放段落

Substitute the values for $\begin{align*}x\end{align*}$ , $\begin{align*}y\end{align*}$ , and  $\begin{align*}m\end{align*}$ that we now have into our $\begin{align*}y=mx+b\end{align*}$ form of the equation of the tangent line:
::将 X 、 y 和 m 的值替换为正切线方程式的 Y = mx+b 形式 :

播放段落

$$\begin{align*}21&=8(4)+b\\ -11&=b\end{align*}$$
::21=8(4)+b-11=b

播放段落

Use the calculated values for  $\begin{align*}m\end{align*}$ and  $\begin{align*}b\end{align*}$ to complete the equation:
::使用 m 和 b 的计算值来完成方程:

播放段落

$$\begin{align*}y=8x-11\end{align*}$$
::y=8x- 11 y=8x- 11

播放段落

Examples
::实例

播放段落

Example 1
::例1

播放段落

Earlier, you were asked how to find the instantaneous speed of an object. Speed is, by definition, a relation between a distance and the time required to cross that distance (recall $\begin{align*}d=rt\end{align*}$ from your science class). If the time required is zero, then you end up dividing by zero, which is undefined.
::早些时候,有人问您如何找到一个对象的瞬时速度。根据定义,速度是距离和穿越距离所需时间(从你的科学课上召回 d=rt)之间的关系。如果所需时间为零,那么最终会以零除以零,而零是未定义的。

播放段落

However, using calculus, you can identify what the end behavior of the function would be if you were to get infinitely close, and thereby effectively calculate the speed at a given instant. In fact, that is exactly what you did in the examples above.
::然而,使用微积分, 您可以确定函数的结束行为是什么样的, 如果您能够完全接近, 从而有效地计算一个特定瞬间的速度。 事实上, 这正是您在上述示例中所做的 。

播放段落

Example 2
::例2

播放段落

Suppose that $\begin{align*}y=x^2-3\end{align*}$
::假设 Y=x2 - 3

播放段落

Find the average rate of change of  $\begin{align*}y\end{align*}$ with respect  $\begin{align*}x\end{align*}$ over the interval [0, 2]. Find the instantaneous rate of change of  $\begin{align*}y\end{align*}$ with respect  $\begin{align*}x\end{align*}$ at the point $\begin{align*}x =-1\end{align*}$ .
::在 [0, 2] 间隔内查找 y 相对于 x 的平均变化速率。在 x 点找到 y 相对于 x 的瞬时变化速率 y 相对于 x x x x 的 秒数 。

播放段落

Applying the formula above for secant with $\begin{align*}f(x)=x^2-3\end{align*}$ and $\begin{align*}x_0=0\end{align*}$ and $\begin{align*}x_1=2\end{align*}$ , yields
::对 f( x) =x2-3 和 x0=0 和 x1=2 的分离值应用上面的公式, 产量

播放段落

$$\begin{align*}m_{sec} &=\frac{f(x_1)-f(x_0)}{t_1-t_0} \\ &=\frac{f(2)-f(0)}{2-0}\\ &=\frac{1-(-3)}{2}\\ &=2\end{align*}$$
::msec=f(x1)-f(x0)-f(x0)-t1-t0=f(2)-f(0)2-0=1-(-3)2=2

播放段落

This means that the average rate of change of $\begin{align*}y\end{align*}$ is 2 units per unit increase in  $\begin{align*}x\end{align*}$ over the interval [0,  2].
::这意味着y的平均变化率为每单位增加2个单位,在[0,2]间隔内增加xx。

播放段落

Recall, for functions of the form $\begin{align*}y=x^2+c\end{align*}$ that $\begin{align*}f^\prime(x)=2x\end{align*}$ ( $\begin{align*}f^\prime (x)\end{align*}$ is “ $\begin{align*}f\end{align*}$ prime of $\begin{align*}x\end{align*}$ ”, meaning “the slope  $\begin{align*}(m)\end{align*}$ of the line tangent to $\begin{align*}x\end{align*}$ ”)
::提醒, y=x2+c 窗体的函数, f=(x)=2x (f=(x) 是“ x 的柱状”, 意指“ 相切线与 x 的斜度(m) ”)

播放段落

$$\begin{align*}m_{tan} &=f^\prime (x_0) \\ &=f^\prime (-1)\\ &=2(-1)\\ &=-2\end{align*}$$
::mtan=f_(x0)=f_(- 1)=2(- 1) @%2

播放段落

This means that the instantaneous rate of change is negative. That is, $\begin{align*}y\end{align*}$ is decreasing at the point $\begin{align*}x = -1\end{align*}$ . It is decreasing at a rate of 2 units per unit increase in $\begin{align*}x\end{align*}$ .
::这意味着瞬时变化速率为负。 也就是说, y 正在下降 x++++1 。 它正在以每单位增加2个单位的速度下降 x 。

播放段落

Example 3
::例3

播放段落

Find the derivative of $\begin{align*}f(x)=\sqrt{x}\end{align*}$ and the equation of the tangent line at $\begin{align*}x_0 = 1\end{align*}$ .
::在 x0=1 时查找 f( x) x 的衍生物和正切线的方程式。

播放段落

Using the definition of the derivative,
::使用衍生物的定义,

播放段落

$$\begin{align*}f^\prime (x) &=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\ &=\lim_{h \to 0} \frac{ \left (\sqrt{x+h} \right )-\sqrt x}{h} \\ &=\lim_{h \to 0}\frac{1}{h}\frac{x+h-x}{\sqrt{x+h} + \sqrt{x}}\\ &=\lim_{h \to 0}\frac{1}{\sqrt{x+h}+\sqrt{x}}\\ &=\frac{1}{2\sqrt{x}}\end{align*}$$
::f_(x) = limh_0f(x+h)(x+h)(x) =limh_0(x+h)(xh=limh_0)(x+h= 01hx+h_x(x) +h_x(x) +h_x(x) =limh_01__x+hx=12__x(x)x

播放段落

Thus, the slope of the tangent line at  $\begin{align*}x_0 = 1\end{align*}$ is
::因此,x0=1的正切线斜坡为

播放段落

$$\begin{align*}f^\prime(1)=\frac{1}{2\sqrt{1}}=\frac{1}{2}\end{align*}$$
::f(1)=121=12

播放段落

For $\begin{align*}x_0 = 1\end{align*}$ , we can find  $\begin{align*}y_0\end{align*}$ by simply substituting into $\begin{align*}f(x)\end{align*}$ :
::对于 x0=1, 我们只需将 Y0 替换为 f( x) 即可找到 y0 :

播放段落

$$\begin{align*}f(x_0) & \equiv y_0 \\ f(1) &=\sqrt{1}=1\\ y_0 &=1 \end{align*}$$
::f( x0) @ y0f(1)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

播放段落

Thus the equation of the tangent line is
::因此,正切线的方程式是

播放段落

$$\begin{align*}y-y_0 &=m(x-x_0)\\ y-1 &=\frac{1}{2}(x-1) \\ y &=\frac{1}{2}x+\frac{1}{2}\end{align*}$$
::yy0=m(x-x0)y- 1=12(x- 1)y=12x+12

播放段落

Example 4
::例4

播放段落

Find the derivative of $\begin{align*}f(x)=\frac{x}{x+1}\end{align*}$
::查找 f( x) =xx+1 的衍生物

播放段落

Using the derivative formula:
::使用衍生公式:

播放段落

$$\begin{align*}f^\prime(x) &=\lim_{h \to 0}\frac{\left [\frac{x+h}{x+h+1}-\frac{x}{x+1} \right ]}{h}\\ &=\lim_{h \to 0}\frac{1}{h}\left[\frac{x+h}{x+h+1}-\frac{x}{x+1}\right ]\\ &=\lim_{h \to 0}\frac{1}{h}\left[\frac{h}{(x+h+1)(x+1)}\right ]\\ &=\lim_{h \to 0}\frac{1}{(x+h+1)(x+1)}\\ &=\frac{1}{(x+1)^2} \end{align*}$$
::f{(x) =limh}0}[x+hx+hx+h+h+h+1+x1+1] [x+hx+h+h+1 -xx+1] =limh#01h[h(x+h+1)(x+1)] =limh}01(x+h+1)(x+h+1) (x+1)=1(x+1) 2

播放段落

Example 5
::例5

播放段落

A particle moves in the positive direction along a straight line so that after  $\begin{align*}t\end{align*}$ nanoseconds, its traversed distance is given by $\begin{align*}\chi (t)=9.9t^3\end{align*}$ nanometers. What is the average velocity of the particle during the first 2 nanoseconds?  What is the instantaneous velocity of the particle at  $\begin{align*}t = 2\end{align*}$ nanoseconds.
::粒子沿着正向直线移动,这样在 t 毫秒后, 其跨度距离由 ( t) = 9. 9T3 毫秒给定。 前 2 毫秒的粒子平均速度是多少? t = 2 毫秒的粒子瞬时速度是多少 。

播放段落

The particle moves $\begin{align*}9.9t^3 \ nm\end{align*}$ in $\begin{align*}t\end{align*}$ secs. 
::粒子在 t 秒内移动9. 9T3 nm。

播放段落

$\begin{align*}\therefore 9.9(2^3)=\frac{79.2 \ nm}{2 \ s}\rightarrow \frac{39.6 \ nm}{1 \ s}\end{align*}$
::9.9(23)=79.2 nm2 s39.6 nm1 s

播放段落

$\begin{align*}\therefore\end{align*}$  The average velocity is 36.9 nm/sec.
::平均速度为36.9纳米/秒。

播放段落

Using the formula for finding the derivative, we get $\begin{align*}\chi ^\prime(t)=29.7 t^2\end{align*}$
::使用寻找衍生物的公式, 我们得到\\( t)=29.7t2

播放段落

$\begin{align*}\therefore \chi ^\prime (2)=118.8 \ nm/s\end{align*}$
:2)=118.8纳米/秒

播放段落

$\begin{align*}\therefore\end{align*}$ The instantaneous velocity at $\begin{align*}t=2\end{align*}$ is 118.8 nm/sec
::T=2的瞬时速度为118.8纳米/秒

播放段落

Review
::回顾

播放段落
1. $\begin{align*}C=f(x)\end{align*}$ and $\begin{align*}f(x)=x^3-4x+2\end{align*}$ . Find the average rate of change of  $\begin{align*}(C)\end{align*}$ with respect to $\begin{align*}(x)\end{align*}$ , when  $\begin{align*}(x)\end{align*}$ is changed from $\begin{align*}x=15\end{align*}$ , to $\begin{align*}x=59\end{align*}$ .
   ::C=f(x)和f(x)=x3-4x+2。 查找(C)相对于(x)的平均变化率, 当(x)从x=15改为x=59。
播放段落
2. $\begin{align*}H=f(x)\end{align*}$ and $\begin{align*}f(x)=x^2-5x+201\end{align*}$ Find the average rate of change of $\begin{align*}(H)\end{align*}$ , with respect to  $\begin{align*}(x)\end{align*}$ when  $\begin{align*}(x)\end{align*}$ is changed from  $\begin{align*}x = 10\end{align*}$ to $\begin{align*}x = 11\end{align*}$ .
   ::H=f(x)和f(x)=x2-5x+201 查找(H)相对于(x)的平均变化率,当(x)从x=10改为x=11时。
播放段落
3. $\begin{align*}N=f(x)\end{align*}$ and $\begin{align*}f(x)=3x^2-4x-1\end{align*}$ Find the average rate of change of  $\begin{align*}(N)\end{align*}$ with respect to  $\begin{align*}(x)\end{align*}$ when  $\begin{align*}(x)\end{align*}$ is changed is changed from  $\begin{align*}x = 20\end{align*}$ to $\begin{align*}x = 64\end{align*}$ .
   ::N=f(x)和f(x)=3x2-4x-1 查找在(x)被更改时对(N)的平均变化率从x=20改为x=64。
播放段落
4. $\begin{align*}H=f(x)\end{align*}$ and $\begin{align*}f(x)=x^2+10x+201\end{align*}$ Find the average rate of change of  $\begin{align*}(H)\end{align*}$ with respect to  $\begin{align*}(x)\end{align*}$ when  $\begin{align*}(x)\end{align*}$ is changed from  $\begin{align*}x = 25\end{align*}$ to $\begin{align*}x = 74\end{align*}$ .
   ::H=f(x) 和 f(x) =x2+10x+201 查找在(x) 从 x=25 改为 x=74 时(x) 相对于 (x) 的平均变化速率 。
播放段落
5. $\begin{align*}N=f(x)\end{align*}$ and $\begin{align*}f(x)=-5x^2-3x-4\end{align*}$ Find the average rate of change of  $\begin{align*}(N)\end{align*}$ with respect to  $\begin{align*}(x)\end{align*}$ when  $\begin{align*}(x)\end{align*}$ is changed from  $\begin{align*}x = 30\end{align*}$ to $\begin{align*}x = 54\end{align*}$ .
   ::N=f(x) 和 f(x) = 5x2-3x-4 查找在(x) 从 x=30 改为 x=54 时对(N) 的平均变化率。
播放段落
6. If $\begin{align*}C=f(x)\end{align*}$ and $\begin{align*}f(x)=-4x^2+2x+5\end{align*}$ , find the instantaneous rate of change of  $\begin{align*}(C)\end{align*}$ with respect to  $\begin{align*}(x)\end{align*}$ when $\begin{align*}x = 25\end{align*}$ .
   ::如果C=f(x)和f(x)=4x2+2x+5,则在x=25时发现相对于(x)的(C)瞬时变化率。
播放段落
7. If $\begin{align*}N=f(x)\end{align*}$ and $\begin{align*}f(x)=3x^2-x-5\end{align*}$ Find the instantaneous rate of change of  $\begin{align*}(N)\end{align*}$ with respect to  $\begin{align*}x\end{align*}$ when $\begin{align*}x = 10\end{align*}$ .
   ::如果 N=f(x) 和 f(x) = 3x2-x-5 查找 x x = 10 时 x (N) 的瞬时变化率 。
播放段落
8. $\begin{align*}H=f(x)\end{align*}$ and $\begin{align*}f(x)=4x^2+195\end{align*}$ Find the instantaneous rate of change of  $\begin{align*}(H)\end{align*}$ with respect to  $\begin{align*}x\end{align*}$ when $\begin{align*}x = 10\end{align*}$ .
   ::H=f(x)和f(x)=4x2+195 查找x=10时x(H)的瞬时变化率。
播放段落
9. $\begin{align*}N=f(x)\end{align*}$ and $\begin{align*}f(x)=-x^2+x-3\end{align*}$ Find the instantaneous rate of change of  $\begin{align*}(N)\end{align*}$ with respect to  $\begin{align*}x\end{align*}$ when $\begin{align*}x=150\end{align*}$ .
   ::N=f(x) 和 f(x) x2+x-3 在 x=150 时查找 x (N) 的瞬时变化率 。
播放段落
10. $\begin{align*}C=f(x)\end{align*}$ and $\begin{align*}f(x)=-3x^2+4x-4\end{align*}$ Find the instantaneous rate of change of  $\begin{align*}(N)\end{align*}$ with respect to  $\begin{align*}x\end{align*}$ when $\begin{align*}x = 20\end{align*}$ .
    ::C=f(x)和f(x)3x2+4x-4 查找x=20时x(N)的瞬时变化率。

播放段落

For #11-16, use the definition of the derivative to find  $\begin{align*}f(x)\end{align*}$ and then find the equation of the tangent line at $\begin{align*}x = x_0\end{align*}$ .
::# 11-16, 使用衍生物的定义查找 f( x), 然后在 x=x0 找到正切线的方程式 。

播放段落
11. $\begin{align*}f(x) = 6x^2\end{align*}$ ; $\begin{align*}x_0 = 3\end{align*}$ .
    :x)=6x2;x0=3;
播放段落
12. $\begin{align*}f(x)=\sqrt{x+2}\end{align*}$ ; $\begin{align*}x_0=8\end{align*}$
    :xx) x+2; x0=8
播放段落
13. $\begin{align*}f(x) = 3x^3 - 2\end{align*}$ ; $\begin{align*}x_0 = -1\end{align*}$
    :x)=3x3-2; x01
播放段落
14. $\begin{align*}f(x)=\frac{1}{x+2}\end{align*}$ ; $\begin{align*}x_0=-1\end{align*}$
    :x) = 1x+2; x0 @% 1
播放段落
15. $\begin{align*}f(x) = ax^2 - b\end{align*}$ , (where  $\begin{align*}a\end{align*}$ and  $\begin{align*}b\end{align*}$ are constants); $\begin{align*}x_0 = b\end{align*}$
    ::f( x) = 轴 - b, (a和b为常数); x0=b
播放段落
16. $\begin{align*}f(x) = x^{\frac{1}{3}}\end{align*}$ ; $\begin{align*}x_0 = 1\end{align*}$ .
    ::f(x) =x13; x0=1;
播放段落
17. A packing company in the south makes “Mama's Spaghetti Sauce”. The cost of producing $\begin{align*}x\end{align*}$ jars is  $\begin{align*}J=f(x)\end{align*}$ dollars. What does  $\begin{align*}f^\prime(100) = 9999\end{align*}$ mean in this context?
    ::南方一家包装公司生产“Mama's Spaghetti Sauce”,生产x罐子的成本为J=f(x)美元,在这方面f=(100)=999999是什么意思?
播放段落
18. A cherry pie is taken from an oven when its temperature is  $\begin{align*}202^\circ F\end{align*}$ and placed on a table in a room where the temperature is $\begin{align*}75^\circ F\end{align*}$ . The temperature of the pie over  $\begin{align*}x\end{align*}$ minutes is given by $\begin{align*}T=f(x)\end{align*}$ . What does  $\begin{align*}f^\prime (100) = -0.6\end{align*}$ mean in this context?
    ::当烤箱温度为202°F时,樱桃馅饼从烤箱中取出,放在一个温度为75°F的房间的桌子上。T=f(x)给出了饼温度超过x分钟的温度。在此情况下,f`(100)0.6意味着什么?
播放段落
19. The number of virus, after  $\begin{align*}(x)\end{align*}$ hours, in a controlled laboratory experiment is $\begin{align*} V=f(x)\end{align*}$ . What are the units of $\begin{align*}f^\prime (x)\end{align*}$ ?
    ::在受控制的实验室实验中,在(x)小时之后的病毒数量是V=f(x). f*(x)的单位是多少?
播放段落
20. The number of people in the US affected by the common cold in the month of November is defined by $\begin{align*}N=f(x) \end{align*}$ where  $\begin{align*}x\end{align*}$ is the day of the month. What is the meaning of  $\begin{align*}f^\prime (x)\end{align*}$ in this context?
    ::N=f(x)定义了11月份美国受普通寒冷影响的人数,而x是月份的一天。 在这方面,f=(x)的含义是什么?
播放段落
21. The number of households in Florida affected by hurricane season in the month of July is defined by  $\begin{align*}J=f(x)\end{align*}$ where  $\begin{align*}x\end{align*}$ is the day of the month and $\begin{align*}f(x)=2x^2+x+1\end{align*}$ . Find the average rate of change of  $\begin{align*}J\end{align*}$ with respect to  $\begin{align*}x\end{align*}$ when days is changed from  $\begin{align*}x=5\end{align*}$ to $\begin{align*}x=34\end{align*}$ .
    ::受7月份飓风季节影响的佛罗里达家庭数目由J=f(x)确定,其中x是月份的一天,f(x)=2x2+x+1。 在x=5到x=34之间,查找J相对于x的平均变化率。
播放段落
22. A cake is taken from an oven when its temperature is  $\begin{align*}196^\circ F\end{align*}$ and placed on a cooling rack in a room where the temperature is $\begin{align*}75^\circ F\end{align*}$ . The temperature of the cake over  $\begin{align*}(x)\end{align*}$ minutes is given by $\begin{align*}H=f(x)\end{align*}$ , where $\begin{align*}f(x)=0.008264x^2-2x+196\end{align*}$ . Find the instantaneous rate of change of  $\begin{align*}H\end{align*}$ with respect to $\begin{align*}x\end{align*}$ when $\begin{align*}x=15\end{align*}$ .
    ::当烤箱温度为196°F时,蛋糕取自烤箱,放在一个温度为75°F的房间的冷却架上。蛋糕在(x)分钟以上的温度由H=f(x)给出,其中f(x)=0.008264x2-2x+196。当 x=15时,找到H相对于x的瞬时变化速率。

播放段落

Review (Answers)
::回顾(答复)

播放段落

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。