节: 优化 | 4.9 优化 | The Way To Learn

章节大纲

At this point, you know how to analyze a function to find its minima and maxima using the first and second . Finding the solution to some real-world problem (such as in finance, science, and engineering) often involves a process of finding the maximum or minimum of a function within an acceptable region of values. This kind of problem is an optimization problem , and the solution that is the maximum or minimum value of the function in the region is the optimal solution . Setting up the optimization problem is the important first step. See if you can setup (but not solve) this problem: What dimensions will minimize the amount of metal required to construct a storage tank of volume $\begin{aligned} 1000 m^{3} \end{aligned}$ that is in the shape of a right circular cylinder and has a top that is a hemisphere?
::此时, 您知道如何用第一和第二步来分析一个函数, 以找到它的迷你和最大值。找到某些现实世界问题( 如金融、科学和工程)的解决方案, 往往需要在一个可接受的价值区域中找到一个最大或最小的函数。此类问题是一个优化问题, 而该地区该函数的最大或最小值是最佳解决方案。设置优化问题是重要的第一步。确定优化问题是重要的第一步。看看您能否设置( 但不是解决) 这一问题: 哪些维度能将建造一个以右圆柱形为形状的1000立方米的储存罐所需的金属量降到最低 ?

Optimization
::优化

In previous concepts, we discussed methods for finding maxima and minima (extrema) of functions, and these methods are used in solving optimization problems. Suppose that $\begin{aligned} f \end{aligned}$ is continuous on a closed interval $\begin{aligned} [a, b] \end{aligned}$ . Recall that we can find the absolute minimum and maximum of a function $\begin{aligned} f \end{aligned}$ that is continuous on a closed interval $\begin{aligned} [a, b] \end{aligned}$ as follows:
::在以前的概念中,我们讨论了找到最大和最小函数的方法,这些方法用于解决优化问题。假设f是在封闭间隔上连续的。回顾我们可以找到在封闭间隔上连续的f函数的绝对最小和最大值,具体如下:

Find the values of $\begin{aligned} f \end{aligned}$ for each critical value in $\begin{aligned} (a, b) \end{aligned}$ ;
::查找(a,b)中每个关键值的 f 值;

Find the values of the function $\begin{aligned} f \end{aligned}$ at the endpoints of $\begin{aligned} [a, b] \end{aligned}$ ;
::在 [a,b] 的终点查找函数 f 的值;

The absolute maximum will be the largest value of the numbers found in 1 and 2; the absolute minimum will be the smallest number.
::绝对上限将是1和2中数字的最大值;绝对最小值将是最小值。

However, real-world problems often impose constraints that must be accounted for in finding the optimal solution.
::然而,现实世界的问题往往造成一些限制因素,在寻找最佳解决办法时必须考虑到这些因素。

Take a company that makes high-quality bicycle tires for both recreational and racing riders. The number of tires that the company sells is a function of the price charged and can be modeled by the formula $\begin{aligned} T (x) = - x^{3} + 36.5 x^{2} + 50 x + 250 \end{aligned}$ , where $\begin{aligned} x \end{aligned}$ is the priced charged for each tire in dollars. At what price is the maximum number of tires sold? How many tires will be sold at that maximum price?
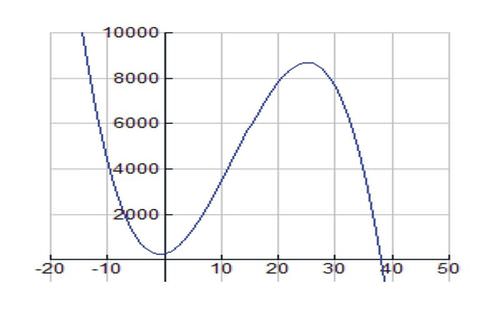
::公司出售的轮胎数量取决于所收价格,可按T(x)x3+36.5x2+50x+250的公式制模。在T(x)x3+36.5x2+50x+250的公式中,x是每台轮胎以美元计价的价格。售出轮胎的最大价格是多少?售出轮胎的最大价格是多少?以这一最高价格出售多少轮胎?

In this optimization problem, we are trying to find the maximum value of $\begin{aligned} T (x) \end{aligned}$ . $\begin{aligned} T (x) \end{aligned}$ is the primary equation that will be optimized. Let’s first look at a graph of the tire function and make some observations. Set the viewing window ranges on your graphing calculator to [-10, 50] for $\begin{aligned} x \end{aligned}$ and [-500, 10000] for $\begin{aligned} y \end{aligned}$ .
::在此优化问题中, 我们正在试图找到 T( x) 的最大值。 T( x) 是将优化的主要方程式。让我们首先查看轮胎功能的图形并做一些观察。将您的图形计算器上的查看窗口范围设置为 x 的 [ 10, 50] 和y 的 [- 500, 1000] 。

The graph should appear as follows:
::图表应如下所示:

We first note that since this is a real-life application, both quantities, $\begin{aligned} x \end{aligned}$ and $\begin{aligned} T (x) \end{aligned}$ , are positive or else the problem makes no sense. These conditions, together with the fact that the zero of $\begin{aligned} T (x) \end{aligned}$ is located at $\begin{aligned} x = 37.9 \end{aligned}$ , suggest that the actual domain of this function is $\begin{aligned} 0 < x \leq 37.9 \end{aligned}$ . This restricted domain, which we refer to as a feasible domain , illustrates a common feature of optimization problems: that the real-life conditions of the situation under study dictate the domain values.
::我们首先注意到,由于这是实际应用,因此X和T(x)数量都是正的,否则问题就毫无意义。这些条件,加上T(x)0位于x=37.9,表明该函数的实际领域为0<x/37.9。我们称之为可行的领域,这一限制性领域显示了优化问题的一个共同特征:所研究情况的实际生活条件决定了域值。

We can use the calculator graph or use the First and Second Derivative Tests to find the absolute maximums and minimums on the closed interval [0, 37.9].
::我们可以使用计算图表,或者使用第一次和第二次衍生试验,在封闭间隔[0, 37.9] 找到绝对最大值和最小值。

1 ^st Derivative

\begin{aligned} f^{'} (x) = - 3 x^{2} + 73 x + 50 \end{aligned}

$\begin{aligned} f^{'} (x) = 0 \end{aligned}$ :
::f_(x)=0:

at $\begin{aligned} x = - \frac{2}{3} \end{aligned}$ ... not in domain;
::x23... 不在域内;

at $\begin{aligned} x = 25 \end{aligned}$ ... in the domain.
::x=25... 在域名中。

2 ^nd Derivative

\begin{aligned} f^{''} (x) = - 6 x + 73 \end{aligned}

$\begin{aligned} f^{''} (25) = 23 \end{aligned}$
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}*(25)=23 {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}*(25)=23

There is a function maximum at $\begin{aligned} x = 25 \end{aligned}$ .
::x=25 有最高值的函数。

We see that the function attains an absolute maximum at $\begin{aligned} x = 25 \end{aligned}$ at the point (25, 8687.5). So, charging a price of $25 will result in a total of 8687 tires being sold.
::我们看到该功能在点(25 8687.5)达到x=25的绝对最高值(25 8687.5)。因此,如果收取25美元的价格,将总共出售8687台轮胎。

In many optimization problems, a secondary equation (or more than one) must be used to reduce the number of variables in the primary equation before starting the optimization procedure (use of a graphing calculator; application of derivative tests).
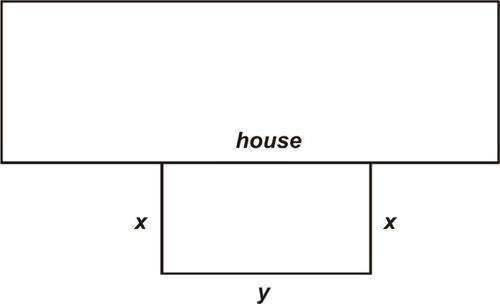
::在许多优化问题中,在开始优化程序(使用图形计算器;应用衍生物测试)之前,必须使用二级方程(或不止一个方程)来减少初级方程中的变量数量。

Suppose that Mary wishes to make an outdoor rectangular pen for her pet chihuahua. She would like the pen to enclose an area in her backyard with one of the sides of the rectangle made by the side of Mary's house as indicated in the following figure. If she has 90 ft of fencing to work with, what dimensions of the pen will result in the maximum area?
::假设Mary想为她的宠物Chihuahua做一个户外长方形笔。她想用钢笔把后院的一块区域围在Mary家旁边的矩形两侧。下图显示,如果她有90英尺的栅栏可以工作,那么钢笔的多少尺寸将达到最大面积?

The dimensions of the pen are $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ in the figure. The primary equation is the function that models the area, $\begin{aligned} A \end{aligned}$ , of the pen. We wish to maximize:
::笔的维度是图中的 x 和 y 。主要的方程式是模拟笔的区域 A 的函数。我们希望最大化 :

\begin{aligned} A = x y . \end{aligned}

::亚历克斯 A=xy.

The secondary equation comes from the information concerning the fencing Mary has to work with. In particular,
::第二等式来自关于Mary围栏的资料。

\begin{aligned} 2 x + y = 90. \end{aligned}

::2x+y=90。

Solving for $\begin{aligned} y \end{aligned}$ we have
::解决你,我们有

\begin{aligned} y = 90 - 2 x . \end{aligned}

::y=90 -2x。 y=90 -2x。

We now substitute into the primary equation to get:
::我们现在用主要方程式来代替:

\begin{aligned} A = x y & = x (90 - 2 x), o r \\ A (x) & = - 2 x^{2} + 90 x \end{aligned}

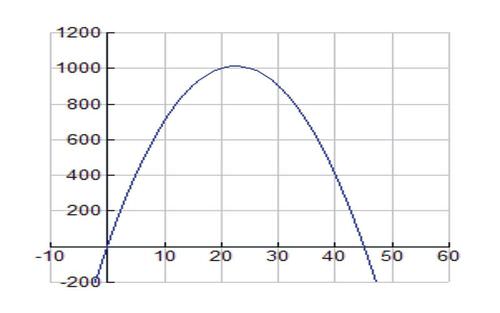
::A=xy=x( 90- 2x) , 或 A( x) % 2x2+90x

It is always helpful to view the graph of the function to be optimized. Set the viewing window ranges on your graphing calculator to [-10, 100] for $\begin{aligned} x \end{aligned}$ and [-500, 1200] for $\begin{aligned} y \end{aligned}$ . The graph should appear as follows:
::查看要优化的函数图形总是有帮助的。将您的图形计算器上的查看窗口区域设置为 x 的 [10, 100] 和 y 的 [- 500, 1200] 。图表应显示如下:

The feasible domain of this function is $\begin{aligned} 0 < x < 45 \end{aligned}$ , which makes sense because if $\begin{aligned} x \end{aligned}$ is 45 feet, then the figure will be two 45-foot-long fences going away from the house with 0 feet left for the width $\begin{aligned} y \end{aligned}$ .
::此函数的可行领域是 0 < x < 45, 这样做是有道理的, 因为如果x为45英尺,那么数字将是两条45英尺长的栅栏,从房子外出去,宽度为5米,只剩下0英尺。

We can find the solution by using the graphing calculator, and/or the First and Second Derivative Tests and the method for finding absolute maximums and minimums on a closed interval (in this problem, [0, 45]).
::我们可以通过图形计算器和(或)第一次和第二次衍生试验以及找到封闭间隔(在此问题上,[0,45])的绝对上限和最小值的方法找到解决办法。

1 ^st Derivative

\begin{aligned} A^{'} (x) = - 4 x + 90 \end{aligned}

$\begin{aligned} A^{'} (x) = 0 \end{aligned}$ :
::A_(x)=0:

at $\begin{aligned} x = 22.5 \end{aligned}$ ... in the domain.
::x=22.5... 在域内。

2 ^nd Derivative

\begin{aligned} A^{''} = - 4 \end{aligned}

$\begin{aligned} A^{''} = - 4 \end{aligned}$
::A4

There is a function maximum at $\begin{aligned} x = 22.5 \end{aligned}$ .
::x=22.5 有最高值的函数。

We see that the function attains an absolute maximum at $\begin{aligned} x = 22.5 \end{aligned}$ at the point (22.5, 1012.5).
::我们看到该函数在x=22.5时达到绝对上限(22.5、1012.5)。

So the dimensions of the pen should be $\begin{aligned} x = 22.5 \end{aligned}$ , and $\begin{aligned} y = 45 \end{aligned}$ ; with those dimensions, the pen will enclose an area of $\begin{aligned} 1012.5 f t^{2} \end{aligned}$ .
::因此,笔的尺寸应该是x=22.5和y=45;用这些尺寸,钢笔将附上面积为1012.5平方英尺的面积。

Optimization problems involving geometric shapes really help illustrate the problem solving process. Here is another:
::与几何形状有关的优化问题确实有助于说明问题的解决过程。

A certain brand of lemonade sells its product in 16-ounce aluminum cans that hold $\begin{aligned} 473 m l (1 m l = 1 c m^{3}) \end{aligned}$ . Find the dimensions of the cylindrical can that will use the least amount of aluminum.
::一定品牌的柠檬以16盎司铝罐出售其产品,含473毫升(1毫升=1立方厘米)。

We need to develop the formula for the surface area of the can. This consists of the top and bottom areas, each $\begin{aligned} π r^{2} \end{aligned}$ , and the surface area of the side, $\begin{aligned} 2 π r h \end{aligned}$ (product of circumference of the top and height of can). Hence the primary equation is
::我们需要为罐体的表面面积制定公式。它包括顶部和底部区域, 每一°r2, 以及侧面的表层区域, 2°rh (罐体顶部和高度环绕的产物) 。因此, 主要的方程是 :

\begin{aligned} A = 2 π r^{2} + 2 π r h . \end{aligned}

::A=2 r2+2 rh.

We observe that both our feasible domains require $\begin{aligned} r, h > 0 \end{aligned}$ .
::我们注意到,我们两个可行的领域都需要r,h>0。

To reduce the number of variables in the primary equation, we need a secondary equation that will give us a relationship between $\begin{aligned} r \end{aligned}$ and $\begin{aligned} h \end{aligned}$ . We note that the volume for a circular cylinder is given by $\begin{aligned} V = π r^{2} h \end{aligned}$ , which provides a relationship between $\begin{aligned} r \end{aligned}$ and $\begin{aligned} h \end{aligned}$ . The secondary equation is:
::为了减少一级等式中的变量数量,我们需要一个二级等式,让我们在r和h之间建立一种关系。我们注意到圆圆柱体的体积是由Vr2h提供的,它提供了r和h之间的关系。

\begin{aligned} h = \frac{V}{π r^{2}} = \frac{473}{π r^{2}} . \end{aligned}

::h=Vr2=473r2。

We substitute this expression for h into the primary equation to get:
::我们用这个表达方式取代h, 将其变成主要方程式, 以获得:

\begin{aligned} A (r) = 2 π r^{2} + 2 π r (\frac{473}{π r^{2}}), o r \\ A (r) = 2 π r^{2} + \frac{946}{r} . \end{aligned}

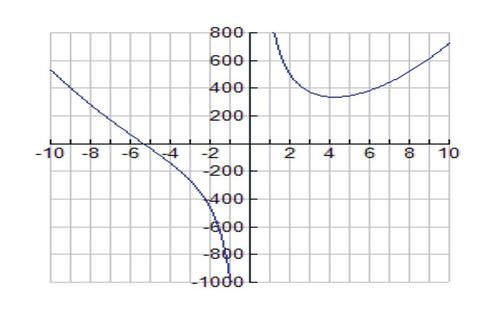
::A(r) = 2.r2+2.r(473°r2),或 A(r) = 2.r2+946r。

The graph of the function $\begin{aligned} A (r) \end{aligned}$ is shown below:
::函数A(r)的图示如下:

The feasible domain is $\begin{aligned} r > 0 \end{aligned}$ .
::可行的域是 r>0。

1 ^st Derivative

\begin{aligned} A^{'} (r) = 4 π r - \frac{946}{r^{2}} \end{aligned}

$\begin{aligned} A^{'} (r) = 0 \end{aligned}$ :
::A_(r)=0:

at $\begin{aligned} r = \sqrt[3]{\frac{946}{4 π}} \approx 4.22 c m \end{aligned}$ ... in the domain.
::在域内 r=9464}3}4.22厘米

2 ^nd Derivative

\begin{aligned} A^{''} (r) = 4 π + \frac{1892}{r^{3}} \end{aligned}

$\begin{aligned} A^{''} (r) > 0 \end{aligned}$ for $\begin{aligned} r > 0 \end{aligned}$
::r>0 的 A(r) > 0

There is a function minimum at $\begin{aligned} r \approx 4.22 c m \end{aligned}$ .
::在 r4.22 cm 有最低功能值。

Hence we have a minimum surface area of $\begin{aligned} 996.2 c m^{2} \end{aligned}$ when $\begin{aligned} r \approx 9.06 c m \end{aligned}$ and $\begin{aligned} h \approx 8.44 c m \end{aligned}$ .
::因此,我们最小表面面积为996.2厘米2,时速为9.06厘米和8.44厘米。

Examples
::实例

Example 1
::例1

Earlier, you were asked about what dimensions will minimize the amount of metal required to construct a storage tank of volume $\begin{aligned} 1000 m^{3} \end{aligned}$ that is in the shape of a right circular cylinder and has a top that is a hemisphere.
::早些时候,有人问到,建造一个以右圆圆柱形为形状、顶部为半球的容量为1000立方米的储存罐,需要多少尺寸才能最大限度地减少所需的金属数量。

The volume of the tank consists of the volume of a cyclinder and the volume of a hemisphere. The volume can be expressed as: $\begin{aligned} V = π r^{2} h + \frac{1}{2} (\frac{4}{3} π r^{3}) = 1000 \end{aligned}$ where $\begin{aligned} r \end{aligned}$ is the radius of the tank (in meters), and $\begin{aligned} h \end{aligned}$ is the cyclinder’s height (in meters).
::罐体的体积由圆柱体的体积和半球的体积组成。其体积可以表现为:Vr2h+12(43r3)=1000,其中r为罐体半径(以米计),h为圆柱体的高度(以米计)。

You would like to minimize the amount of metal used, which is the same as asking to minimize the area of the tank. This should be the optimization problem statement.
::您想要尽量减少所使用的金属量, 这与要求将罐体面积最小化相同。这应该是优化问题声明。

The area can be expressed as: $\begin{aligned} A = 2 π r h + \frac{1}{2} (4 π r^{2}) \end{aligned}$ . Because there are two variables, $\begin{aligned} r \end{aligned}$ and $\begin{aligned} h \end{aligned}$ , we should make $\begin{aligned} h \end{aligned}$ a function $\begin{aligned} r \end{aligned}$ , i.e., $\begin{aligned} h (r) \end{aligned}$ , using the equation for $\begin{aligned} V \end{aligned}$ .
::区域可表述为:A=2rh+12(4r2)。由于有两种变量,即r和h,我们应使用V的方程式,使 h 成为函数 r,即h(r) 。

\begin{aligned} h (r) = \frac{1000}{π r^{2}} - \frac{2}{3} r \end{aligned}

::h(r)=1000-r2-23r

The optimization problem statement is then:
::优化问题说明如下:

\begin{aligned} \frac{d A}{d r} = 0 = \frac{d}{d r} [2 π r h (r) + \frac{1}{2} (4 π r^{2})] & = 2 π [h (r) + r \frac{d h}{d r} + 2 r], o r \\ h (r) + r \frac{d h}{d r} + 2 r & = 0. \end{aligned}

::dAdr=0=ddr[2rh(r)+12(4r2)=2[h(r)+rdhdr+2r],或h(r)+rdhdr+2r=0。

The next step is to solve the optimization problem to see if there is a solution that makes sense. Can you do it?
::下一步是解决优化问题,看看是否有一个合理的解决方案。你能做到这一点吗?

Example 2
::例2

A storage bin is to be constructed having a rectangular base, rectangular sides, and open at the top. Its width is 4 meters and its volume is 36 cubic meters. If building the bin costs $10/sq. m. for the base and $5/sq. m. for the sides, what is the cost of the least expensive bin? What are its dimensions?
::存储箱将建造成一个长方形底座、长方形侧面、顶部打开。它的宽度是4米,体积是36立方米。如果建造这个底座需要10美元/平方米,侧面需要5美元/平方米,那么最便宜的垃圾箱的成本是多少?它的尺寸是多少?

Let the dimensions of the bin be $\begin{aligned} l \end{aligned}$ length, $\begin{aligned} w \end{aligned}$ width, and $\begin{aligned} h \end{aligned}$ height. Note that $\begin{aligned} w = 4 \end{aligned}$ meters.
::让文件夹的尺寸为 I 长度、 w 宽度和 h 高度。注意 w= 4 公尺。

The primary equation is the function that models the cost, C , of the bin. We wish to minimize:
::主要方程式是计算垃圾箱成本C的函数。我们希望最小化 :

\begin{aligned} C = 10 l w + 5 [2 l h + 2 w h] = 10 [l w + l h + w h] = 10 [4 l + l h + w h] \end{aligned}

::C=10lw+5[2lh+2wh]=10[lw+lh+wh]=10[4l+lh+wh]

The secondary equation comes from the information concerning the volume of the bin:
::第二等式来自关于垃圾箱容量的信息 :

\begin{aligned} V = l w h = 4 l h = 36. \end{aligned}

::V=lwh=4lh=36。 =lwh=4lh=36。 =lwh=4lh=36。

Using the secondary equation in the primary equation:
::在主等式中使用第二等式:

\begin{aligned} C = 10 [4 l + l h + w h] = 10 [4 l + \frac{36}{4} + \frac{36}{l}] = 40 [l + 2.25 + \frac{9}{l}] \end{aligned}

::C=10[4l+lh+wh]=10[4l+364+36l]=40[l+2.25+9l]

We can find the solution by using the First and Second Derivative Tests and the method for finding absolute maximums and minimums on a closed interval (in this problem, [0, 45]).
::我们可以利用第一和第二次衍生试验和在封闭间隔内找到绝对上限和最低限数的方法(在此问题上,[0,45])来找到解决办法。

1 ^st Derivative ::第 1 条衍生	$\begin{aligned} C^{'} (l) = 40 (1 - \frac{9}{l^{2}}) \end{aligned}$ ::C*(l)=40(1-9l2)	$\begin{aligned} C^{'} (l) = 0 \end{aligned}$ : at $\begin{aligned} l = 3 \end{aligned}$ (in the domain) and $\begin{aligned} l = - 3 \end{aligned}$ (not in domain). ::C=0:l=3(在域内)和l=3(不在域内)。
2 ^nd Derivative ::第2类衍生物	$\begin{aligned} C^{''} (l) = \frac{720}{l^{3}} \end{aligned}$ ::C(l)=720l3	$\begin{aligned} C^{''} (3) \approx 26.7 \end{aligned}$ . . . Cost function is concave upward . ::C(3)26.7 . 成本函数向上累积。 There is a function minimum at $\begin{aligned} l = 3 \end{aligned}$ . ::在l=3时至少有一个函数值。

1 ^st Derivative
::第 1 条衍生

$\begin{aligned} C^{'} (l) = 40 (1 - \frac{9}{l^{2}}) \end{aligned}$
::C*(l)=40(1-9l2)

$\begin{aligned} C^{'} (l) = 0 \end{aligned}$ : at $\begin{aligned} l = 3 \end{aligned}$ (in the domain) and $\begin{aligned} l = - 3 \end{aligned}$ (not in domain).
::C=0:l=3(在域内)和l=3(不在域内)。

2 ^nd Derivative
::第2类衍生物

$\begin{aligned} C^{''} (l) = \frac{720}{l^{3}} \end{aligned}$
::C(l)=720l3

$\begin{aligned} C^{''} (3) \approx 26.7 \end{aligned}$ . . . Cost function is concave upward .
::C(3)26.7 . 成本函数向上累积。

There is a function minimum at $\begin{aligned} l = 3 \end{aligned}$ .
::在l=3时至少有一个函数值。

So the dimensions of the bin are: $\begin{aligned} l = 3 \end{aligned}$ meters, $\begin{aligned} w = 4 \end{aligned}$ meters, and $\begin{aligned} h = 3 \end{aligned}$ meters.
::垃圾箱的尺寸是: 1=3米, w=4米, h=3米。

The cost to build the bin: $\begin{aligned} C (3) = $ 40 (3 + 2.25 + 3) = $ 330 \end{aligned}$ .
::建造垃圾箱的费用:C(3)=40美元(3+2.25+3)=330美元。

Review
::回顾

For #1-4, find the absolute maximum and absolute minimum values, if they exist.
::对于 #1-4, 找到绝对最高和绝对最低值, 如果有的话。

$\begin{aligned} f (x) = 2 x^{2} - 6 x + 6 \end{aligned}$ on [0, 5]
::f(x) = 2x2 - 6x+6 时 [ 0, 5]

$\begin{aligned} f (x) = x^{3} + 3 x^{2} \end{aligned}$ on [-2, 3]
::f(x) =x3+3x2, [- 3]

$\begin{aligned} f (x) = 3 x^{\frac{2}{3}} - 6 x + 6 \end{aligned}$ on [1, 8]
::f( x) = 3x23 - 6x+6 时 [ 1, 8]

$\begin{aligned} f (x) = x^{4} - x^{3} \end{aligned}$ on [-2, 2]
:xx)=x4-x3 [-2, 2]

Find the dimensions of a rectangle having area $\begin{aligned} 2000 f t^{2} \end{aligned}$ whose perimeter is as small as possible.
::找到一个矩形的尺寸,其面积为2000平方英尺,其周界越小越好。

Find two numbers whose product is 50 and whose sum is a minimum.
::找到两个数字,其产品为50,其总和是最低的。

John is shooting a basketball from half-court. It is approximately 45 ft from the half court line to the hoop. The function $\begin{aligned} s (t) = - 0.025 t^{2} + t + 15 \end{aligned}$ models the basketball’s height above the ground $\begin{aligned} s (t) \end{aligned}$ in feet, when it is $\begin{aligned} t \end{aligned}$ feet from the hoop. How many feet from John will the ball reach its highest height? What is that height?
::约翰正从半场拍摄篮球。从半场到篮球大约45英尺。函数S( t) 0.025t2+t+15 模拟篮球在地面( t) 脚上的高度, 当篮球距离篮球圈是 t 脚的时候。球离约翰多远才能达到最高高度? 高度是多少?

The height of a model rocket $\begin{aligned} t \end{aligned}$ seconds into flight is given by the formula $\begin{aligned} h (t) = - \frac{1}{3} t^{3} + 4 t^{2} + 25 t + 4 \end{aligned}$ .
1. How long will it take for the rocket to attain its maximum height?
  ::火箭达到最大高度需要多长时间?
2. What is the maximum height that the rocket will reach?
  ::火箭将达到的最高高度是多少?
3. How long will the flight last?
  ::飞行还要持续多久?
::模型火箭 t 飞行的高度由公式 h( t) = 13t3+4t2+25t+4给出。火箭达到最大高度需要多长时间? 火箭达到的最高高度是多少? 飞行持续多久?

Show that of all rectangles of a given perimeter, the rectangle with the greatest area is a square.
::显示给定周边的所有矩形, 最大区域的矩形是方形。

Show that of all rectangles of a given area, the rectangle with the smallest perimeter is a square.
::显示给定区域的所有矩形, 最小周边的矩形为正方形。

Eduardo wants to build a fence which will protect his rectangular tomato garden from the various hungry critters roaming the landscape. He purchases 100 feet of fence. What should the dimensions of the tomato garden be if it is to have the maximum area that can be contained by 100 feet of fence.
::Eduardo想建造一道栅栏,保护他的长方形番茄花园不受各种饥饿动物的侵扰。他购买了100英尺长的栅栏。如果番茄花园拥有最多100英尺长的栅栏,那么其尺寸应该如何?

Hans has been challenged to find two nonnegative numbers whose sum is 36 so that the product of the two numbers is maximal. How should he proceed?
::汉斯被要求找到两个非负数, 其总数是36, 这样两个数的产物是最高值。他应该怎么继续呢?

Lucia needs to find two nonnegative numbers whose product is 25 so that the sum of one plus the square of the other is minimized, in order to gain membership to a club. What numbers is she after?
::圣卢西亚需要找到两个非负数,其产品为25个,以便尽量减少一个加一个平方的总和,从而获得俱乐部会员资格。

Esmeralda wants to enclose a field with a rectangular fence to keep her goats from escaping. One side of the field is against a building, so it will not require fencing. She has 50 feet of fencing material. What are dimensions of the maximum area she can fence?
::Esmeralda想用长方形栅栏围着一块田地,防止她的山羊逃跑。一面的田地对着一座建筑,所以不需要围栏。她有50英尺的栅栏材料。她能围住的最大面积是多少?

Which point on the graph of the function $\begin{aligned} y = \sqrt{x} \end{aligned}$ is closest to the point (1, 0)?
::函数 y=x 的图形中哪个点最接近点(1, 0) ?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Optimization ::优化

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Review ::回顾

Review (Answers) ::回顾(答复)

Optimization
::优化

Examples
::实例

Example 1
::例1

Example 2
::例2

Review
::回顾

Review (Answers)
::回顾(答复)