节: 函数的近似根根 : 牛顿的方法 | 4.11 函数的近似根根:牛顿方法

章节大纲

We want to look at finding the roots of a polynomial. Sometimes the polynomial cannot be easily factored, and other algebraic methods (e.g., the quadratic equation) are not applicable, or do not work. When faced with a mathematical problem that cannot be solved with simple algebraic means, calculus sometimes provides a way of finding approximate solutions.
::我们想要寻找多元数学的根。有时,多元数学不能很容易地被考虑在内,而其他代数方法(如二次方程)则不适用,或者无效。当数学问题无法用简单的代数方法解决时,计算有时会提供找到近似解决方案的途径。

Newton's Method
::牛顿方法

A simple example will help introduce Newton’s Method for approximating the roots of a polynomial equation.
::一个简单的例子将有助于引入牛顿的“接近多面方程式根部的方法 ” 。

Let's say you want to compute $\begin{aligned} \sqrt{5} \end{aligned}$ without using a calculator or a table. Any ideas how this could be done? Try thinking about this problem in a different way, so that you make use of linearization .
::假设您想要计算 5 而不使用计算器或表格。任何想法如何做到这一点? 尝试用不同的方式来思考这个问题, 这样您就可以使用线性化。

Assume that we are interested in solving the quadratic equation:
::假设我们有兴趣解决二次方程式:

\begin{aligned} f (x) = x^{2} - 5 = 0 \end{aligned}

xx) =x2-5=0

We know this equation has the roots $\begin{aligned} x = \pm \sqrt{5} \end{aligned}$ .
::我们知道这个方程式有根 x5。

The idea here is to find the linearization of $\begin{aligned} f (x) \end{aligned}$ at an appropriate point, and then solve the linear equation for $\begin{aligned} x \end{aligned}$ . This is an added twist to the linearization problem!
::这里的想法是在一个适当点找到 f( x) 的线性化, 然后解开 x 的线性方程。这是线性化问题的额外转折 !

How to choose the linearization point? Since $\begin{aligned} \sqrt{4} < \sqrt{5} < \sqrt{9} \end{aligned}$ , this mean $\begin{aligned} 2 < \sqrt{5} < 3 \end{aligned}$ .
::如何选择线性点? 自 4 < 5 < 9, 这意味着 2 < 5 < 3 。

We choose the linear approximation of $\begin{aligned} f (x) \end{aligned}$ to be near $\begin{aligned} x_{0} = 2 \end{aligned}$ (but, $\begin{aligned} x_{0} = 3 \end{aligned}$ could also could be selected).
::我们选择 f(x) 的线性近似值, 以接近 x0=2 (但也可以选择 x0=3) 。

$\begin{aligned} f (x) = x^{2} - 5 \end{aligned}$ and $\begin{aligned} f (2) = - 1 \end{aligned}$
:xx)=x2-5和f(2)1

$\begin{aligned} f^{'} (x) = 2 x \end{aligned}$ and $\begin{aligned} f^{'} (2) = 4 \end{aligned}$ .
::f_(x)=2x和f_(2)=4。

Using the linear approximation formula,
::使用线性近似公式,

\begin{aligned} f (x) & \approx f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) \\ \approx - 1 + (4) (x - 2) \\ \approx - 1 + 4 x - 8 \\ \approx 4 x - 9. \end{aligned}

xx) f(x0)+f*(x0)+f*(x0)(x-x0)\*1+(4)(x-2)\*1+4x-8*4x-9。

Notice that this equation is much easier to solve than $\begin{aligned} f (x) = x^{2} - 5 = 0 \end{aligned}$ .
::注意此方程比 f( x) =x2 - 5=0 更容易解析。

Setting $\begin{aligned} f (x) = 0 \end{aligned}$ and solving for $\begin{aligned} x \end{aligned}$ , we obtain,
::设置 f(x)=0 和解析 x, 我们获得,

\begin{aligned} 4 x - 9 & = 0 \\ x & = \frac{9}{4} \\ = 2.25. \end{aligned}

::4-9=0x=94=2.25。

This is a fairly good approximation, since a calculator would give $\begin{aligned} x = 2.23607 \end{aligned}$ , lower by 0.014. We can actually make this approximation to the root of $\begin{aligned} f (x) \end{aligned}$ even better by repeating what we have just done but using the latest estimate $\begin{aligned} x_{1} = 2.25 = \frac{9}{4} \end{aligned}$ , a number that is even closer to the actual value of $\begin{aligned} \sqrt{5} \end{aligned}$ .
::这是一个相当不错的近似值, 因为计算器会给出 x=2.23607, 低于 0.014 。我们实际上可以通过重复我们刚才所做的, 来使f( x) 根的近似值更好, 但使用最新的估计值 x1= 2. 25=94, 这个数字更接近于实际值为 5 。

$\begin{aligned} f (x) = x^{2} - 5 \end{aligned}$ and $\begin{aligned} f (2.25) = \frac{1}{16} \end{aligned}$
:xx)=x2-5和f(2.25)=116

$\begin{aligned} f^{'} (x) = 2 x \end{aligned}$ and $\begin{aligned} f^{'} (2) = \frac{9}{2} \end{aligned}$
::f_(x)=2x和f_(2)=92

Using the linear approximation again,
::再次使用线性近似,

\begin{aligned} f (x) & \approx f (x_{1}) + f^{'} (x_{1}) (x - x_{1}) \\ \approx \frac{1}{16} + \frac{9}{2} (x - \frac{9}{4}) \\ \approx \frac{9}{2} x - \frac{161}{16} . \end{aligned}

::f(x) f(x1) +f*(x1)(x1)(x-x1) 116+92(x-94) 92x-16116。

Solving for $\begin{aligned} x \end{aligned}$ by setting $\begin{aligned} f (x) = 0 \end{aligned}$ , we obtain
::设置 f(x)=0, 溶解 x 的 f(x)=0, 我们获得

\begin{aligned} x = x_{2} = \frac{161}{72} = 2.23611 \end{aligned}

::x=x2=16172=2.23611

which is an even better approximation than $\begin{aligned} x_{1} = \frac{9}{4} \end{aligned}$ .
::比x1=94更接近。

We could continue this process generating a better approximation to $\begin{aligned} \sqrt{5} \end{aligned}$ , as shown in the table, where the last estimate approximates the correct answer to 5 places. Thank goodness for calculators!
::我们可以继续这一进程,从而更接近于5,如表所示,最后的估计接近于5个地方的正确答案。感谢计算者!

$\begin{aligned} n \end{aligned}$ ::n 内	$\begin{aligned} x_{n} \end{aligned}$ ::xn 进	$\begin{aligned} f (x_{n}) \end{aligned}$ :fxn)	$\begin{aligned} f^{'} (x_{n}) \end{aligned}$ ::f_( xn)	$\begin{aligned} \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ :fxn) f_(xn)	$\begin{aligned} x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ ::xn-f(xn) f_(xn)
1	2	-1	4	-0.25	2.25
2	2.25	0.0625	4.5	0.01389	2.23611
3	2.23611	0.00019	4.47222	0.00004	2.23607
4	2.23607	--	--	--	--

This is the basic idea of Newton’s Method . Here is a summary of the method:
::这是牛顿方法的基本概念。以下是方法摘要:

Given the function $\begin{aligned} f (x) \end{aligned}$ , find $\begin{aligned} f^{'} (x) \end{aligned}$ .
::根据函数 f(x),请查找 f_(x) 。

Estimate the first approximation, $\begin{aligned} x_{0} \end{aligned}$ , to a solution of the equation $\begin{aligned} f (x) = 0 \end{aligned}$ . Use a graph to help in finding the first approximation if necessary (see Figure below).
::估计第一个近似值为x0, 以解析公式 f(x)=0。必要时使用图表帮助寻找第一个近近近值(见下图)。

Use the current approximation $\begin{aligned} x_{n} \end{aligned}$ to find the next approximation, $\begin{aligned} x_{n + 1} \end{aligned}$ , by using the recursion relation.
::使用当前近似 xn 使用递归关系查找下一个近似 xn+1 。

\begin{aligned} x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} . \end{aligned}

::xn+1=xn-f(xn)f_(xn)xn。

Repeat the previous step until the desired level of convergence occurs.
::重复前一步骤,直至达到预期的趋同水平。

Note that in some cases, Newton’s Method does not converge .
::请注意,在一些情况下,牛顿的方法并不趋同。

Examples
::实例

Example 1
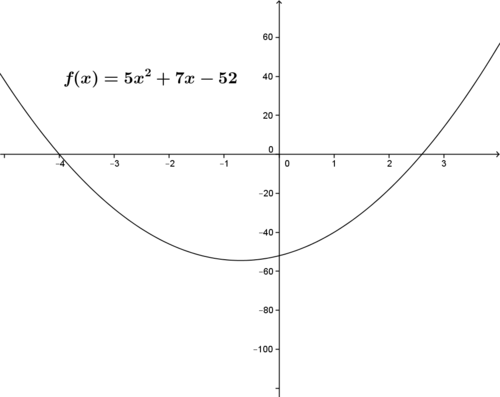
::例1

Compare the solutions to $\begin{aligned} f (x) = 5 x^{2} + 7 x - 52 \end{aligned}$ in the interval [2, 3] from using the Quadratic formula and using Newton’s Method.
::将使用二次曲线公式和使用牛顿方法的(x)=5x2+7x-52的间隔[2, 3]中的 f(x)=5x2+7x-52的解决方案比较。

The function is shown in the figure.
::函数在图中显示。

For $\begin{aligned} f (x) = 5 x^{2} + 7 x - 52 = 0 \end{aligned}$ , use of the quadratic formula gives the exact solution $\begin{aligned} x = 2.6 \end{aligned}$ in the interval.
::对于 f(x) = 5x2+7x-52=0, 使用四方形公式给出准确的溶液x=2.6 间隔。

Use of Newton’s Method with an initial estimate of $\begin{aligned} x_{0} = 3 \end{aligned}$ , yields the results shown in the table.
::使用牛顿方法,初步估计为x0=3,得出表中所列结果。

$\begin{aligned} n \end{aligned}$ ::n 内	$\begin{aligned} x_{n} \end{aligned}$ ::xn 进	$\begin{aligned} f (x_{n}) \end{aligned}$ :fxn)	$\begin{aligned} f^{'} (x_{n}) \end{aligned}$ ::f_( xn)	$\begin{aligned} \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ :fxn) f_(xn)	$\begin{aligned} x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ ::xn-f(xn) f_(xn)
1	3	14	37	0.3784	2.6216
2	2.6216	0.7151	33.216	0.0215	2.6001
3	2.6001	0.0033	33.001	0.0001	2.6000
4	2.6000	--	--	--	--

The technique rapidly converges to a solution.
::技术迅速趋于一致,找到解决办法。

Example 2
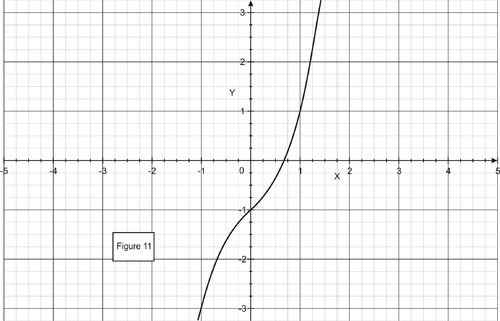
::例2

Use Newton’s method to find the roots of the polynomial $\begin{aligned} f (x) = x^{3} + x - 1 \end{aligned}$ .
::使用牛顿的方法来查找 monnomilal f( x) =x3+x-1 的根根。

The problem is to solve the equation $\begin{aligned} f (x) = x^{3} + x - 1 = 0 \end{aligned}$ .
::问题是解决f(x)=x3+x- 1=0的方程式。

The equations we need are:
::我们需要的方程式是:

$\begin{aligned} f (x) = x^{3} + x - 1 \end{aligned}$
:xx)=x3+x-1)

$\begin{aligned} f^{'} (x) = 3 x^{2} + 1 \end{aligned}$ .
::f_(x) = 3x2+1 。

Using the recursion relation,
::使用循环关系,

\begin{aligned} x_{n + 1} & = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} \\ = x_{n} - \frac{x_{n}^{3} + x_{n} - 1}{3 x_{n}^{2} + 1} . \end{aligned}

::xn+1=xn-f(xn)f_(xn)=xn-xn3+xn-13xn2+1。

To help us find the first approximation, we make a graph of $\begin{aligned} f (x) \end{aligned}$ . As the figure suggests, set $\begin{aligned} x_{1} = 0.6 \end{aligned}$ .
::为了帮助我们找到第一个近似值, 我们绘制一个 f( x) 的图形。如图所示, 设置 x1=0. 6 。

Then using the recursion relation, we can generate $\begin{aligned} x_{1} \end{aligned}$ :
::然后使用循环关系, 我们可以生成x1 :

\begin{aligned} x_{n + 1} & = x_{n} - \frac{x_{n}^{3} + x_{n} - 1}{3 x_{n}^{2} + 1} \\ x_{2} & = 0.6 - \frac{(0.6)^{3} + (0.6) - 1}{3 (0.6)^{2} + 1} \\ = 0.6884615. \end{aligned}

::xn+1=xn-xn3+xn-13xn2+1x2=0.6-(0.6)3+(0.6)-13(0.6)2+1=0.6884615。

By using the recursion relation several times, we can find $\begin{aligned} x_{3} \end{aligned}$ and $\begin{aligned} x_{4} \end{aligned}$ as shown in the table.
::通过多次使用递归关系,我们可以找到表所示的 x3 和 x4 。

$\begin{aligned} n \end{aligned}$ ::n 内	$\begin{aligned} x_{n} \end{aligned}$ ::xn 进	$\begin{aligned} f (x_{n}) \end{aligned}$ :fxn)	$\begin{aligned} f^{'} (x_{n}) \end{aligned}$ ::f_( xn)	$\begin{aligned} \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ :fxn) f_(xn)	$\begin{aligned} x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ ::xn-f(xn) f_(xn)
1	0.6	-0.184	2.08	-0.0884615	0.6884615
2	0.6884615	0.01477796	2.4219377	0.0061017	0.6823598
3	0.6823598	0.00007669	2.3968445	0.0000320	0.6823278
4	0.6823278	--	--	--	--

We conclude that the solution to the equation $\begin{aligned} x^{3} + x - 1 = 0 \end{aligned}$ is about 0.6823.
::我们的结论是,公式x3+x-1=0的解决方案约为0.6823。

Example 3
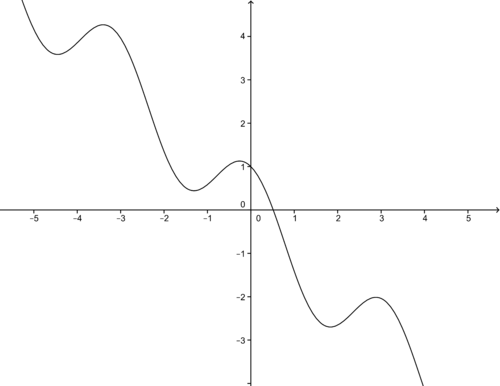
::例3

Use Newton’s Method to show to find the root of $\begin{aligned} f (x) = \cos (2 x) - x \end{aligned}$ .
::使用牛顿的方法来显示 f( x) = cos *( 2x) - x 的根。

The equations we need are:
::我们需要的方程式是:

$\begin{aligned} f (x) = \cos (2 x) - x \end{aligned}$
:xx) =cos(2x)-x

$\begin{aligned} f (x) = - 2 \sin (2 x) - 1 \end{aligned}$
:xx)%2sin(2x)- 1

Using the recursion relation,
::使用循环关系,

\begin{aligned} x_{n + 1} & = x_{n} \frac{f (x_{n})}{f^{'} (x_{n})} \\ = x_{n} - \frac{\cos (2 x_{n}) - x_{n}}{- 2 \sin (2 x_{n}) - 1} \end{aligned}

::xn+1=xnf( xn) f*( xn) =xn-cos *( 2xn)-xn-2sin *( 2xn)- 1

To help us find the first approximation, we make a graph of $\begin{aligned} f (x) \end{aligned}$ . As the figure suggests, set the first estimate at 0.5.
::为了帮助我们找到第一个近似值,我们绘制一个f(x)的图表。如图所示,将第一个估计数定为0.5。

Using the recursion relation several times gives the table values:
::使用递归关系多次给出表格值:

$\begin{aligned} n \end{aligned}$ ::n 内	$\begin{aligned} x_{n} \end{aligned}$ ::xn 进	$\begin{aligned} f (x_{n}) \end{aligned}$ :fxn)	$\begin{aligned} \frac{f (x_{n})}{f^{'} (x_{n})} \end{aligned}$ :fxn) f_(xn)
1	0.500000	0.0403023	-0.0152168
2	0.515022	-0.0002400	0.0000884
3	0.514933	-0.0000000	0.0000000
4	0.514933	--	--

We conclude that the solution to the equation $\begin{aligned} \cos (2 x) - x = 0 \end{aligned}$ is 0.514933.
::我们的结论是,对等方程的解决方案为0.514933,cos(2x)-x=0。

Review
::回顾

For all the problems, use Newton’s Method to find the roots.
::使用牛顿的方法找出根源。

$\begin{aligned} x^{3} + 3 = 0 \end{aligned}$ .
::x3+3=0。

$\begin{aligned} - x + 3 \sqrt{- 1 + x} = 0 \end{aligned}$ .
::-x+3-1+x=0。

$\begin{aligned} 4 x^{2} - x - 2 \end{aligned}$ in the interval [-1, 0].
::间距[-1,0]4x2-x-2。

$\begin{aligned} 4 x^{3} - 6 x^{2} - 1 \end{aligned}$ .
::4x3 - 6x2 - 1;

$\begin{aligned} 5 e^{- x} + x^{3} \end{aligned}$ .
::5 e- x+x3 。

$\begin{aligned} \cos x - x \end{aligned}$ .
::xxxx。

$\begin{aligned} x^{5} - 7 x^{2} + 2 \end{aligned}$ in the interval [-1, 0].
::间隔[-1,0] x5-7x2+2。

$\begin{aligned} x^{5} - 7 x^{2} + 2 \end{aligned}$ in the interval [0, 1].
::x5-7x2+2 间隔 [0, 1] 。

$\begin{aligned} x^{2} \cos x - x \end{aligned}$ in the interval [4, 5].
::间隔内 x2cosx-x [4, 5] 。

$\begin{aligned} x^{2} \cos x - x \end{aligned}$ in the interval [7, 8].
::间隔中的 x2cosx-x [7、8] 。

$\begin{aligned} f (x) = x - 2 \sin (x) \end{aligned}$ to five decimal places, starting with initial guess $\begin{aligned} x_{0} = 3 \end{aligned}$ .
::f(x) =x- 2sin(x) 到小数点后五位位数, 从最初的猜测x0=3开始。

$\begin{aligned} f (x) = 6 x^{3} - 4 x + 1 \end{aligned}$ to three decimal places, starting with initial guess $\begin{aligned} x_{0} = 1.2 \end{aligned}$ .
::f(x) = 6x3 - 4x+1 到小数点后三位位数, 从初始猜数x0=1.2开始。

$\begin{aligned} f (x) = \ln (x) \times (\ln (x) + 4) + 1 \end{aligned}$ to five decimal places, starting with initial guess $\begin{aligned} x_{0} = 1 \end{aligned}$ .
::f(x) = ln (x) ×(ln (x)+4)+1 到小数点后五个位数, 从最初的猜测x0=1开始。

$\begin{aligned} f (x) = \tan (x) - \csc (x) \end{aligned}$ to six digits of accuracy, starting with initial guess $\begin{aligned} x_{0} = 0.7 \end{aligned}$ .
::f(x)=tan(x)-csc(x)至精度的六位数,从最初的猜测x0=0.7开始。

$\begin{aligned} f (x) = \tan^{- 1} (x) + \cos (x) \end{aligned}$ to four digits of accuracy, starting with initial guess $\begin{aligned} x_{0} = - 2 \end{aligned}$ .
::f(x) = tan- 1(x) +cos(x) 至 4 位数的精确度, 从初始猜数 x02 开始。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Newton's Method ::牛顿方法

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Review ::回顾

Review (Answers) ::回顾(答复)