节: 两个曲线之间的区域 | 6.1 两个曲线之间的面积

章节大纲

Earlier , the definite integral of a function over an interval was presented as the in the interval. This interpretation of the definite integral provides a method to find the area of two-dimensional figures that is quite different than the use of the simple geometric formulas associated with finding the areas of figures made up of polygons and circles. Using what you know about the definite integral, can you formulate a general procedure to find the area of shapes defined by two curves?
::早些时候,一个间隔函数的确定组成部分被显示为间隔中。对确定组成部分的这一解释提供了一种方法,用以查找与使用简单的几何公式有关的二维数字区域,该二维数字区域与查找由多边形和圆形组成的数字区域相当不同。你对确定组成部分所了解的情况,能否制定一个一般程序来查找由两个曲线定义的形状区域?

Area Between Two Curves
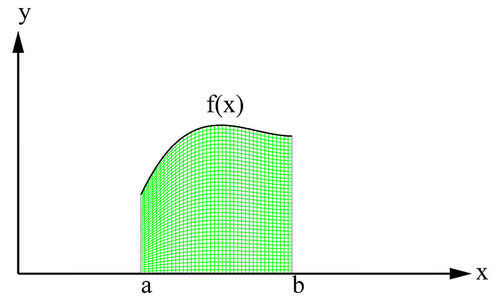
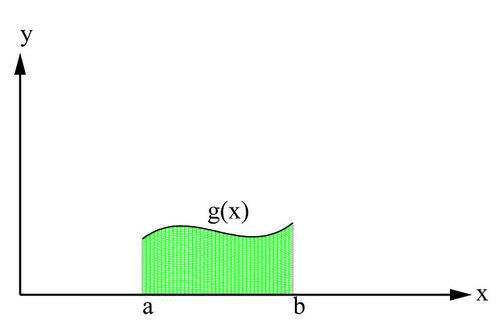
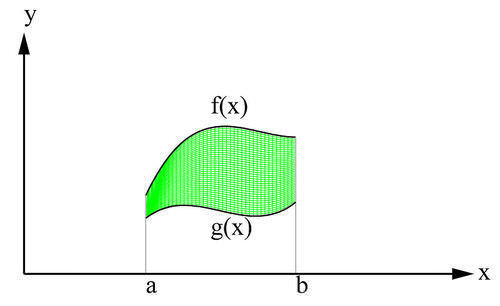
::两个曲线之间的区域

Consider the region bounded by the graphs $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ between $\begin{aligned} x = a \end{aligned}$ and $\begin{aligned} x = b \end{aligned}$ , as shown in the figures below. If the two graphs lie above the $\begin{aligned} x \end{aligned}$ -axis, we can interpret the area that is sandwiched between them as the area under the graph of $\begin{aligned} g \end{aligned}$ subtracted from the area under the graph $\begin{aligned} f \end{aligned}$ .
::考虑下图所示的 x=a 和 x=b 之间受图表 f 和 g 之间的区域。如果两个图表位于 x 轴上方,我们可以将它们之间夹杂的区域解释为从图f 下区域中减去的 g 的图下区域。

Therefore, as the graphs show, it makes sense to say that
::因此,如图表所示,可以说

[Area under $\begin{aligned} f \end{aligned}$ (Fig. 6.1.1a)] - [Area under $\begin{aligned} g \end{aligned}$ (Fig. 6.1.1b)] = [Area between $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ (Fig.6.1.1c)],
::[f类区域(图6.1.1a)]-[g类区域(图6.1.1b)]=[f类和g类区域(图6.1.1c)],

$\begin{aligned} \int_{a}^{b} f (x) d x = \int_{a}^{b} g (x) = \int_{a}^{b} [f (x) - g (x)] d x . \end{aligned}$

::-=YTET -伊甸园字幕组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=-

This relation is valid as long as the two functions are continuous and the upper function $\begin{aligned} f (x) \geq g (x) \end{aligned}$ on the interval $\begin{aligned} [a, b] \end{aligned}$ .
::只要两个函数是连续的,而上函数 f(x)\g(x)在间隔[a,b]上方函数f(x)\g(x),则此关系有效。

Using the information from above, find the area of the region enclosed between $\begin{aligned} f (x) = 3 x + 5 \end{aligned}$ and $\begin{aligned} g (x) = x^{2} \end{aligned}$ in the interval [1, 3].
::使用上述信息,在间隔[1、3]中找到f(x)=3x+5和g(x)=x2之间的区域区域。

First make a sketch of the region. As you can see from the graph, $\begin{aligned} f (x) > g (x) \end{aligned}$ in the interval [1, 3]. Applying the area formula,
::首先绘制区域草图。从图形中可以看到, 间距 [1, 3] 中的 f( x) > g( x)。应用区域公式,

$\begin{aligned} A & = \int_{a}^{b} [f (x) - g (x)] d x \\ = \int_{1}^{3} [(3 x + 5) - (x^{2})] d x \\ = {[\frac{3 x^{2}}{2} + 5 x - \frac{x^{3}}{3}]}_{1}^{3} \\ = \frac{40}{3} \end{aligned}$

::Aab[f(x)-g(x) dx=13[(3x+5)-(x2+5)dx=[3x22+5x-x33]13=403

So the area between the two curves $\begin{aligned} f (x) = 3 x + 5 \end{aligned}$ and $\begin{aligned} g (x) = x^{2} \end{aligned}$ in the interval [1, 3].
::因此,两个曲线 f( x) =3x+5 和 g( x) =x2 之间的区域在间隔[ 1, 3] 中。

At times, the interval of integration of the two curves $\begin{aligned} f (x) \end{aligned}$ and $\begin{aligned} g (x) \end{aligned}$ may be determined by points of intersection between the two curves. In addition, the points of intersection may be where the two curves change their relationship with respect to which is larger. There may be a need to change the difference expression in the integrand .
::有时,两个曲线f(x)和g(x)的整合间隔可能由两个曲线之间的交叉点决定,此外,两个曲线的交叉点可能是两个曲线改变关系关系较大之处,可能需要改变整数的差别表达式。

Examples
::实例

Example 1
::例1

Earlier, you were asked whether you could formulate a general procedure to find the area of shapes defined by two curves (functions). If you said to just find the area of the separate curves and subtract the results, then your strategy is basically correct.
::早些时候,有人问您是否可以制定一个一般程序来查找由两个曲线(函数)定义的形状区域。如果你说只要找到单独的曲线区域并减去结果,那么您的策略基本上是正确的。

A general approach would consist of:
::一般做法包括:

Sketching the curves that define the figure
::筛选用于定义图形的曲线

Deciding on integration along the $\begin{aligned} x \end{aligned}$ - or $\begin{aligned} y \end{aligned}$ -axis
::决定如何沿 x 或 Y 轴进行整合

Writing out the integrand as the difference of functions
::将整数写成函数的区别

Determining the limits of integration (interval)
::确定整合的限度(间隔)

Integrating to find the area
::集成以寻找区域

Example 2
::例2

Find the area of the region enclosed between $\begin{aligned} y = x^{2} \end{aligned}$ and $\begin{aligned} y = x + 6 \end{aligned}$ .
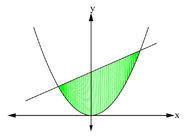
::查找 y=x2 和 y=x+6 之间的区域区域。

First make a sketch of the region and find the end points of the interval of integration. To do so, we simply equate the two functions, $\begin{aligned} x^{2} = x + 6 \end{aligned}$ , and solve for $\begin{aligned} x \end{aligned}$ .
::首先绘制区域草图并找到整合间隔的终点。为此, 我们只需将两个函数( x2=x+6) 等同起来, 然后解决 x 。

$\begin{aligned} x^{2} - x - 6 & = 0 \\ (x + 2) (x - 3) & = 0 \end{aligned}$

::x2 - x - 6=0( x+2)( x-3)=0

From which we get $\begin{aligned} x = - 2 \end{aligned}$ and $\begin{aligned} x = 3 \end{aligned}$ .
::从中我们获得 x2 和 x=3 。

So the upper and lower boundaries intersect at points (-2, 4) and (3, 9).
::因此,上界和下界在点(-2,4)和点(3,9)相互交错。

As you can see from the graph, $\begin{aligned} x + 6 \geq x^{2} \end{aligned}$ and hence $\begin{aligned} f (x) = x + 6 \end{aligned}$ and $\begin{aligned} g (x) = x^{2} \end{aligned}$ in the interval [-2, 3]. Applying the area formula,
::从图中可以看出,在间隔[-- 3] 中 x+6xx2 和 f(x)=x6 和 g(x)=x2。应用区域公式,

$\begin{aligned} A & = \int_{a}^{b} [f (x) - g (x)] d x \\ = \int_{- 2}^{3} [(x + 6) - (x^{2})] d x . \end{aligned}$

::Aab[f(x)-g(x) dx23[(x+6)-(x2)dx]。

Integrating,
::融合,

$\begin{aligned} A & = {[\frac{x^{2}}{2} + 6 x - \frac{x^{3}}{3}]}_{- 2}^{3} \\ = \frac{125}{6} . \end{aligned}$

::A=[x22+6x-x33]-23=1256.

So the area between the two curves $\begin{aligned} f (x) = x + 6 \end{aligned}$ and $\begin{aligned} g (x) = x^{2} \end{aligned}$ is $\begin{aligned} \frac{125}{6} \end{aligned}$ .
::因此,两个曲线f(x)=x+6和g(x)=x2之间的区域为1256。

Sometimes there is a need to find the area under the curve with respect to the $\begin{aligned} y \end{aligned}$ -axis instead of the $\begin{aligned} x \end{aligned}$ -axis, as is depicted below.
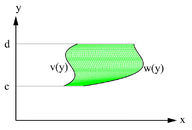
::有时需要从Y轴曲线下找到区域,而不是X轴,如下文所述。

In this case, the interval of integration is on the $\begin{aligned} y \end{aligned}$ -axis, and the equations of the curves must be written in such a way that they are expressed explicitly as a function of $\begin{aligned} y \end{aligned}$ . The area between the curves is then written as follows:
::在此情况下,整合的间隔在 Y 轴上,曲线的方程必须写成,以y的函数表示。然后,曲线之间的区域写成如下:

dy-%5Cint%20%5Climits_c%5Ed%20vdy%3D%5Cint%20%5Climits_c%5Ed%20%5Bw-v%5Ddy">
$\begin{aligned} A = \int_{c}^{d} w (y) d y - \int_{c}^{d} v (y) d y = \int_{c}^{d} [w (y) - v (y)] d y \end{aligned}$

::Acdwdycdvdycd[w-v]dy

Example 3
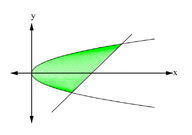
::例3

Find the area of the region enclosed by $\begin{aligned} x = y^{2} \end{aligned}$ and $\begin{aligned} y = x - 6 \end{aligned}$ .
::查找 x=y2 和 y=x-6 所附加的区域区域。

As you can see from the figure, the left boundary is $\begin{aligned} x = y^{2} \end{aligned}$ and the right boundary is $\begin{aligned} y = x - 6 \end{aligned}$ . The points of intersection of the two curves determine that the interval of integration extends over the interval $\begin{aligned} - 2 \leq y \leq 3 \end{aligned}$ . However, we must express the equations in terms of $\begin{aligned} y \end{aligned}$ . We rewrite
::从图中可以看到,左边边界为 x=y2,右边边界为 y=x-6。两个曲线的交叉点决定了融合的间隔跨到- 2 3。然而,我们必须用y表示方程。我们重写

$\begin{aligned} x & = y^{2} \\ x & = y + 6. \end{aligned}$

::x=y2x=y+6 。

Thus,
::因此,

-v%5Ddy%20%5C%5C%0A%26%3D%5Cint%20%5Climits%20_%7B-2%7D%5E3%20%5B(y%2B6)-(y%5E2)%5Ddy%20%5C%5C%0A%26%3D%5Cleft%5B%5Cfrac%7By%5E2%7D%7B2%7D%2B6y-%5Cfrac%7By%5E3%7D%7B3%7D%20%5Cright%5D_%7B-2%7D%5E3%20%5C%5C%0AA%20%26%3D%5Cfrac%7B125%7D%7B6%7D">
$\begin{aligned} A & = \int_{c}^{d} [w (y) - v (y)] d y \\ = \int_{- 2}^{3} [(y + 6) - (y^{2})] d y \\ = {[\frac{y^{2}}{2} + 6 y - \frac{y^{3}}{3}]}_{- 2}^{3} \\ A & = \frac{125}{6} \end{aligned}$

::Acd[w-v] dy23[(y+6)-(y2)]dy=[y22+6y-y33]-23A=1256

So the area between the two curves $\begin{aligned} y = x - 6 \end{aligned}$ and $\begin{aligned} x = y^{2} \end{aligned}$ is $\begin{aligned} \frac{125}{6} \end{aligned}$ .
::因此,两个曲线 y=x-6 和 x=y2 之间的区域为 1256。

Example 4
::例4

Find the area between the curves $\begin{aligned} y = x + 1 \end{aligned}$ and $\begin{aligned} y = x^{3} + x^{2} - x + 1 \end{aligned}$ between the intersection points.
::查找交叉点之间曲线 y=x+1 和 y=x3+x2-x+1 之间的区域。

Find points of intersection:
::查找交叉点 :

$\begin{aligned} x + 1 & = x^{3} + x^{2} - x + 1 \\ 0 & = x^{3} + x^{2} - 2 x \\ 0 & = x (x^{2} + x - 2) = x (x + 2) (x - 1) \\ x & = - 2, x = 0, x = 1 \end{aligned}$

::x+1=x3+x2=x3+x2=x2=10=x3+x2=x2=2x0=xx(x2+x-2)=xx(x+2)(x-1)x2,x=0,x=1

On the first interval, $\begin{aligned} (x^{3} + x^{2} - x + 1) \geq (x + 1) \end{aligned}$ ; on the second, $\begin{aligned} (x + 1) \geq (x^{3} + x^{2} - x + 1) \end{aligned}$ . To find the total area, compute:
::在第一个间隔, (x3+x2- x+1)\(x+1)\(x+1)\(x+1)\(x+1)\(x3+x2- x+1)\(x+1), 找到总区域, 计算 :

$\begin{aligned} A & = \int_{- 2}^{0} [g (x) - f (x)] d x + \int_{0}^{1} [f (x) - g (x)] d x \\ = \int_{- 2}^{0} [(x^{3} + x^{2} - x + 1) - (x + 1)] d x + \int_{0}^{1} [(x + 1) - (x^{3} + x^{2} - x + 1)] d x \\ = \int_{- 2}^{0} (x^{3} + x^{2} - 2 x) d x + \int_{0}^{1} - (x^{3} + x^{2} - 2 x) d x \\ A & = (\frac{1}{4} x^{4} + \frac{1}{3} x^{3} - x^{2}) |_{- 2}^{0} - (\frac{1}{4} x^{4} + \frac{1}{3} x^{3} - x^{2}) |_{0}^{1} \\ = \frac{8}{3} - (- \frac{5}{12}) \\ A & = \frac{37}{12} \end{aligned}$

::A20[g(xx)-f(x)dxx************************************************************************************************************** ***********************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************

The area between the curves $\begin{aligned} y = x + 1 \end{aligned}$ and $\begin{aligned} y = x^{3} + x^{2} - x + 1 \end{aligned}$ over the interval [-2, 1] is $\begin{aligned} \frac{37}{12} \end{aligned}$ .
::y=x+1和y=x3+x2-x+1之间的间距[-2,1]之间的区域为3712。

Review
::回顾

For #1-7, sketch the region enclosed by the curves and find the area.
::1 -7, 绘制曲线覆盖的区域图, 并找到区域。

$\begin{aligned} y = x^{2} \end{aligned}$ , $\begin{aligned} y = \sqrt{x} \end{aligned}$ , on the intero view the Explore Moreval [0.25, 1].
::y=x2, y=x, 在 intero 视图中, 探索 Moreval [0. 25, 1] 。

$\begin{aligned} y = 0 \end{aligned}$ , $\begin{aligned} y = \cos 2 x \end{aligned}$ , on the interval $\begin{aligned} [\frac{π}{4}, \frac{π}{2}] \end{aligned}$ .
::y=0,y=cos2x,在间隔[%4,%2]。

$\begin{aligned} y = | - 1 + x | + 2 \end{aligned}$ , $\begin{aligned} y = \frac{- 1}{5} x + 7 \end{aligned}$ .
::y1+x%2,y=15x+7。

$\begin{aligned} y = \cos x \end{aligned}$ , $\begin{aligned} y = \sin x \end{aligned}$ , $\begin{aligned} x = 0 \end{aligned}$ , $\begin{aligned} x = 2 π \end{aligned}$ .
::y=cos=x,y=sin=xx,x=0,x=2。

$\begin{aligned} x = y^{2} \end{aligned}$ , $\begin{aligned} y = x - 2 \end{aligned}$ integrate with respect to $\begin{aligned} y \end{aligned}$ .
::x=y2, y=x-2 与y有关的整合。

$\begin{aligned} y^{2} - 4 x = 4 \end{aligned}$ , $\begin{aligned} 4 x - y = 16 \end{aligned}$ integrate with respect to $\begin{aligned} y \end{aligned}$ .
::y2-4x=4、4x-y=16结合与y有关。

$\begin{aligned} y = 8 \cos x \end{aligned}$ , $\begin{aligned} y = \sec^{2} x \end{aligned}$ , $\begin{aligned} \frac{- π}{3} \leq x \leq \frac{π}{3} \end{aligned}$ .
::y=8cos* x,y=sec2*x, y=3x*3。

Find the area enclosed by $\begin{aligned} x = y^{3} \end{aligned}$ and $\begin{aligned} x = y \end{aligned}$ .
::查找 x=y3 和 x=y 所覆盖的区域。

If the area enclosed by the two functions $\begin{aligned} y = k \cos x \end{aligned}$ and $\begin{aligned} y = k x^{2} \end{aligned}$ is 2, what is the value of $\begin{aligned} k \end{aligned}$ ?
::如果两个函数 y=kcosx 和 y=kx2 所覆盖的区域为 2, k 值是多少 ?

Find the horizontal line $\begin{aligned} y = k \end{aligned}$ that divides the region between $\begin{aligned} y = x^{2} \end{aligned}$ and $\begin{aligned} y = 9 \end{aligned}$ into two equal areas.
::查找将 y=x2 和 y=9 之间的区域分隔为两个等值区域的水平线 y=k。

Find the area between the curves $\begin{aligned} y = s i n (x) \end{aligned}$ and $\begin{aligned} y = x \sqrt{x^{2} + 1} + 2 \end{aligned}$ between the points $\begin{aligned} x = 0 \end{aligned}$ and $\begin{aligned} x = π \end{aligned}$ .
::在 y=sin(x) 和 y=x22+1+2 之间,在点 x=0 和 x 之间查找曲线 y=sin(x) 和 y=x2+1+2 之间的区域。

Find the area of bounded by the following: $\begin{aligned} y = 1 \end{aligned}$ , $\begin{aligned} y = π \end{aligned}$ , $\begin{aligned} y = x^{3} + 9 \end{aligned}$ , $\begin{aligned} y = \frac{1}{x} \end{aligned}$ .
::查找以下区域之间的区域:y=1,y,y=3+9,y=1x。

Find the points of intersection of the curves $\begin{aligned} y = 5 x \end{aligned}$ and $\begin{aligned} y = 4 x^{2} - 6 \end{aligned}$ .
::查找曲线y=5x和y=4x2-6的交叉点。

Find the area between the curves $\begin{aligned} y = x^{2} \end{aligned}$ and $\begin{aligned} y = 8 - x^{2} \end{aligned}$ .
::查找曲线 y=x2 和 y= 8-x2 之间的区域。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

Area Between Two Curves ::两个曲线之间的区域

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Area Between Two Curves
::两个曲线之间的区域

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)